Astronomy & Astrophysics Integrated Photometric Characteristics of Galactic Open Star Clusters
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Photometric and Spectroscopic Study of the Southern Open Clusters Pismis 18, Pismis 19, Ngc 6005, and Ngc 6253 Andre S E
THE ASTRONOMICAL JOURNAL, 116:801È812, 1998 August ( 1998. The American Astronomical Society. All rights reserved. Printed in U.S.A. A PHOTOMETRIC AND SPECTROSCOPIC STUDY OF THE SOUTHERN OPEN CLUSTERS PISMIS 18, PISMIS 19, NGC 6005, AND NGC 6253 ANDRE S E. PIATTI1,2 AND JUAN J. CLARIA 2 Observatorio Astrono mico, Universidad Nacional de Co rdoba, Laprida 854, 5000 Co rdoba, Argentina; andres=oac.uncor.edu, claria=oac.uncor.edu EDUARDO BICA2 Departamento de Astronomia, Universidade Federal do Rio Grande do Sul, C.P. 15051, Porto Alegre, 91500-970, RS, Brazil; bica=if.ufrgs.br DOUG GEISLER Kitt Peak National Observatory, National Optical Astronomy Observatories, P.O. Box 26732, Tucson, AZ 85726; doug=noao.edu AND DANTE MINNITI Lawrence Livermore National Laboratory, L-413, P.O. Box 808, Livermore, CA 94550; dminniti=igpp.llnl.gov Received 1997 October 3; revised 1998 April 24 ABSTRACT CCD observations in the B, V , and I passbands have been used to generate color-magnitude diagrams (CMDs) for the southern open cluster candidates Pismis 18, Pismis 19, and NGC 6005, as well as for the old open cluster NGC 6253. The sample consists of about 1550 stars reaching down to V D 19 mag. From analysis of the CMDs, the physical reality of the three cluster candidates is conÐrmed and their reddening, distance, and age are derived, as well as those of NGC 6253. In addition, integrated spectra for Pismis 18, Pismis 19, and NGC 6253 covering a range from 3500 to 9200A were obtained. The reddening, age, and metallicity of these three clusters were derived from Balmer and Ca II triplet equiva- lent widths by comparing the observed spectra with those of template clusters. -

Deep Sky Explorer Atlas
Deep Sky Explorer Atlas Reference manual Star charts for the southern skies Compiled by Auke Slotegraaf and distributed under an Attribution-Noncommercial 3.0 Creative Commons license. Version 0.20, January 2009 Deep Sky Explorer Atlas Introduction Deep Sky Explorer Atlas Reference manual The Deep Sky Explorer’s Atlas consists of 30 wide-field star charts, from the south pole to declination +45°, showing all stars down to 8th magnitude and over 1 000 deep sky objects. The design philosophy of the Atlas was to depict the night sky as it is seen, without the clutter of constellation boundary lines, RA/Dec fiducial markings, or other labels. However, constellations are identified by their standard three-letter abbreviations as a minimal aid to orientation. Those wishing to use charts showing an array of invisible lines, numbers and letters will find elsewhere a wide selection of star charts; these include the Herald-Bobroff Astroatlas, the Cambridge Star Atlas, Uranometria 2000.0, and the Millenium Star Atlas. The Deep Sky Explorer Atlas is very much for the explorer. Special mention should be made of the excellent charts by Toshimi Taki and Andrew L. Johnson. Both are free to download and make ideal complements to this Atlas. Andrew Johnson’s wide-field charts include constellation figures and stellar designations and are highly recommended for learning the constellations. They can be downloaded from http://www.cloudynights.com/item.php?item_id=1052 Toshimi Taki has produced the excellent “Taki’s 8.5 Magnitude Star Atlas” which is a serious competitor for the commercial Uranometria atlas. His atlas has 149 charts and is available from http://www.asahi-net.or.jp/~zs3t-tk/atlas_85/atlas_85.htm Suggestions on how to use the Atlas Because the Atlas is distributed in digital format, its pages can be printed on a standard laser printer as needed. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Deepsky Observer's Companion
Deepsky Observer’s Companion Auke Slotegraaf Director: Deepsky Observing Section, Astronomical Society of Southern Africa 2002 December Deepsky Observers Companion | 1 1 Deepsky observing for the beginner Some thoughts on 1.1 Just starting out in astronomy? taking up astronomy as a hobby. The following thoughts and suggestions on as- 6. Find other amateurs. “Self-education is tronomy as a hobby have been adapted from an fine as far as it goes, but there’s nothing like article by Alan McRobert (1994) in Sky & Tel- sharing an interest with others.” escope. 7. When it’s time for a telescope, plunge in 1. Ransack your public library. “Astronomy deep. Don’t skimp on quality. “The telescope is a learning hobby ... self-education is some- you want has two essentials. One is a solid, thing you do yourself, with books, using the steady, smoothly working mount. The other is “Two things fill high-quality optics ... You may also want large the mind with ever library.” aperture (size), but don’t forget portability and new and increasing 2. Learn the sky with the naked eye. “As- convenience.” admiration and tronomy is an outdoor nature hobby. Go into awe, the oftener and the night and learn the starry names and pat- 8. Lose your ego. “Astronomy teaches pa- the more steadily terns overhead.” tience and humility - and you’d better be pre- we reflect on them: pared to learn them ... The universe will not 3. Don’t rush to buy a telescope. “To put a the starry heavens bend to your wishes; you must take it on its telescope to rewarding use, you first need to above and the mor- own terms. -

The Bennett Catalogue
The Bennett Catalogue www.macastro.org.au Catalogue Numbers Type R.A. Dec. U2000 Con. Ben 1 NGC 55 Gal 0:14:54 -39:11 386 Scl Ben 2 NGC 104 GC 0:24:06 -72:05 440 Tuc Ben 3 NGC 247 Gal 0:47:06 -20:46 306 Cet Ben 4 NGC 253 Gal 0:47:36 -25:17 306 Scl Ben 5 NGC 288 GC 0:52:48 -26:35 307 Scl Ben 6 NGC 300 Gal 0:54:54 -37:41 351 Scl Ben 7 NGC 362 GC 1:03:12 -70:51 441 Tuc Ben 8 NGC 613 Gal 1:34:18 -29:25 352 Scl Ben 9 NGC 1068 Gal 2:42:42 -00:01 220 Cet Ben 10 NGC 1097 Gal 2:46:18 -30:17 354 For Ben 10a NGC 1232 Gal 3:09:48 -20:35 311 Eri Ben 11 NGC 1261 GC 3:12:18 -55:13 419 Hor Ben 12 NGC 1291 Gal 3:17:18 -41:08 390 Eri Ben 13 NGC 1313 Gal 3:18:18 -66:30 443 Ret Ben 14 NGC 1316 Gal 3:22:42 -37:12 355 For Ben 14a NGC 1350 Gal 3:31:06 -33:38 355 For Ben 15 NGC 1360 PN 3:33:18 -25:51 312 For Ben 16 NGC 1365 Gal 3:33:36 -36:08 355 For Ben 17 NGC 1380 Gal 3:36:30 -34:59 355 For Ben 18 NGC 1387 Gal 3:37:00 -35:31 355 For Ben 19 NGC 1399 Gal 3:38:30 -35:27 355 For Ben 19a NGC 1398 Gal 3:38:54 -26:20 312 For Ben 20 NGC 1404 Gal 3:38:54 -35:35 355 Eri Ben 21 NGC 1433 Gal 3:42:00 -47:13 391 Hor Ben 21a NGC 1512 Gal 4:03:54 -43:21 391 Hor Ben 22 NGC 1535 PN 4:14:12 -12:44 268 Eri Ben 23 NGC 1549 Gal 4:15:42 -55:36 420 Dor Ben 24 NGC 1553 Gal 4:16:12 -55:47 420 Dor Ben 25 NGC 1566 Gal 4:20:00 -54:56 420 Dor Ben 25a NGC 1617 Gal 4:31:42 -54:36 421 Dor Ben 26 NGC 1672 Gal 4:45:42 -59:15 421 Dor Ben 27 NGC 1763 BN 4:56:48 -66:24 444 Dor Ben 28 NGC 1783 GC 4:58:54 -66:00 444 Dor Ben 29 NGC 1792 Gal 5:05:12 -37:59 358 Col -

Jack Bennett's Catalogue of Southern Comet-Like Deep-Sky Objects
Jack Bennett’s Catalogue of Southern Comet-like Deep-sky Objects Deep-sky Observing Challenge Compiled by Auke Slotegraaf Director: ASSA Deep-Sky Observing Section. Version 4.2, November 2013 Jack Bennett and his catalogue For two decades, starting in the late 1960’s, the southern sky was patrolled by a dedicated South African comet-hunter named Jack Bennett. He observed from his urban backyard with a 5-inch low-power refractor. Not only did he discover two comets, he also picked up a 9th magnitude supernova in NGC 5236 (M83), becoming the first person ever to visually discover a supernova since the invention of the telescope. Bennett was born on April 6th, 1914 and passed away on May 30th, 1990. A long-standing member of the Astronomical Society of Southern Africa (ASSA), he was elected President in 1969. The Society awarded him the prestigious Gill Medal for services to astronomy in 1970 and in 1986 he received an Honorary Degree of Master of Science from the University of Witwatersrand. In 1989, at the recommendation of Rob McNaught of Siding Springs Observatory, the asteroid VD 4093 was named after him. Bennett was a skilled observer and in the spirit of Charles Messier drew up two lists of southern objects that appeared comet-like in his telescope. His first list (Bennett, 1969) was published four months before he discovered his first comet. The supplementary list (Bennett, 1974) was followed three months later by his second discovery. In his 1969 Presidential Address to the ASSA Bennett said: “As an aid to the recognition of comet-like objects in the Southern sky, and to help observers to eliminate them in comet searches, I have over the past five years compiled a list of 130 such objects visible south of the celestial equator. -

Mass Segregation in Diverse Environments
Mass segregation in diverse environments Priya Hasan1 and S N Hasan2 Department of Astronomy, Osmania University, Hyderabad - 500007, India. Abstract In this paper, using 2MASS photometry, we study the mass functions φ(M)= dN/dM ∝ M −α of a sample of nine clusters of ages varying from 4 Myr–1.2 Gyr and Galactocentric distances from 6–12 kpc. We look for evidence of mass segregation in these clusters by tracing the variation in the value of α in different regions of the cluster as a function of the parameter τ = tage/trelax (where tage is the age of the cluster and trelax is the relaxation time of the cluster), Galactocentric distance, age and size of the cluster. The value of α value increases with age and τ and fits straight lines with slopes m and y-intercepts c given by m = 0.40 ± 0.03, c = −1.86±0.27 and m = 0.01±0.001, c = −0.85±0.02, respectively and is a clear indicator of the dynamical processes involved. The confidence level of the Pearson’s product-moment correlation of α with age is 0.76 with p=0.002 and with τ is 0.71 with p=0.007. The value of α also increases with Galactocentric distance, indicating the presence of a larger relative number of low mass stars in clusters at larger Galactocentric distances. We find two clusters, viz. IC 1805 and NGC 1893, with evidence of primordial or early dynamical mass segregation. Implications of primordial mass segregation on the formation of massive stars and recent results supporting early dynamical mass segregation are discussed. -
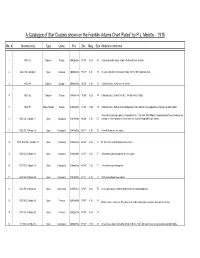
A Catalogue of Star Clusters Shown on the Franklin-Adams Chart Plates” by P.J
A Catalogue of Star Clusters shown on the Franklin-Adams Chart Plates” by P.J. Melotte – 1915 Mel. # Alternative(s) Type Const. R.A. Dec. Mag. Size Melotte's comments 1 NGC 104 Globular Tucana 00h24m04s -72°05' 4.00 50' A typical globular cluster. Bright. Well condensed at centre. 2 NGC 188, Collinder 6 Open Cepheus 00h47m28s +85°15' 9.30 17' "A somewhat ill-defined cluster mostly 14th to 16th magnitude stars. 3 NGC 288 Globular Sculptor 00h52m45s -26°35' 8.10 13' Globular cluster, rather loose at centre. 4 NGC 362 Globular Tucana 01h03m14s -70°50' 6.80 14' Globular cluster. Similar to N.G.C. 104 but smaller. Bright. 5 NGC 371 Diffuse Nebula Tucana 01h03m30s -72°03' 13.80 7.5' Globular cluster. Falls in smaller Magellanic cloud, and has every appearance of being a globular cluster. A few stars clustering together. Resembles N.G.C. 582, 645, 659. Difficult to decide whether these should not be 6 NGC 436, Collinder 11 Open Cassiopeia 01h15m58s +58°48' 9.30 5.0' classed II. All the clusters here resemble one another though differing in extent. 7 NGC 457, Collinder 12 Open Cassiopeia 01h19m35s +58°17' 5.10 20' A small cluster in a rich region. 8 M103, NGC 581, Collinder 14 Open Cassiopeia 01h33m23s +60°39' 6.90 5' M. 103. A few stars forming a loose cluster. 9 NGC 654, Collinder 18 Open Cassiopeia 01h44m00s +61°53' 8.20 5' A few stars clustered together in a rich region. 10 NGC 659, Collinder 19 Open Cassiopeia 01h44m24s +60°40' 7.20 5' A few stars clustered together. -
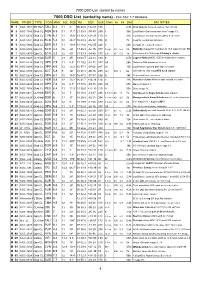
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

The Gaia-ESO Survey – November 2017 Progress Report
The Gaia-ESO Survey – November 2017 progress report 1) Survey observations progress 2) iDR5 products internal release 3) Plans for iDR6 4) Reports to ESO and Phase 3 releases 5) Science projects and publications 6) Jobs The Gaia-ESO Public Spectroscopic Survey started more than 5 years ago, and was celebrated with Newsletter Number 1. This is Newsletter 8, where we summarize the progress made since March 2017. We remind everyone that all the Survey policy, progress, and activity is recorded on the Survey wiki, available at http://great.ast.cam.ac.uk/GESwiki/GESHome. An account there will keep you up to date. More general information is also available on the public web pages http://www.gaia-eso.eu 1. Survey observation progress 320 nights have been completed; the final 20 ones have been scheduled in November and December 2017, and January 2018. The night of January 25-26 2018 will be the last of the Survey, after six years. These last three runs will be mostly dedicated to open cluster observations. No updates are needed on the cluster sample and MW fields observed up to now, since no new observations were performed since our last Newsletter in March 2017. Up to date information on the observing runs, and the survey progress and observed fields is available at the WG0 wiki. A list of the observed open clusters and calibration targets is also available there. A list of cluster targets still to be observed can be found on WG4 wiki, where also the relevant information and reports on the clusters and cluster targets can be found. -
Arxiv:2103.06004V2 [Astro-Ph.SR] 23 Mar 2021 That Can Place It Above the CMD TO
Astronomy & Astrophysics manuscript no. 40072corr ©ESO 2021 March 24, 2021 A new, Gaia-based, catalogue of blue straggler stars in open clusters M.J. Rain1, J.A. Ahumada2,, and G. Carraro1 1 Dipartimento di Fisica e Astronomia, Universita’ di Padova, Vicolo Osservatorio 3, I-35122, Padova, Italy e-mail: [email protected] 2 Observatorio Astronómico, Universidad Nacional de Córdoba, Laprida 854, X5000BGR, Córdoba, Argentina Received September 15, 1996; accepted March 16, 1997 ABSTRACT Context. Blue straggler stars are exotic objects present in all stellar environments whose nature and formation channels are still partially unclear. They seem to be particularly abundant in open clusters (OCs), thus offering a unique chance to tackle these problems statistically. Aims. We aim to build up a new and homogeneous catalogue of blue straggler stars (BSS) in Galactic OCs using Gaia to provide a more solid assessment of the membership of these stars. We also aim to explore possible relationships of the straggler abundance with the parent cluster’s structural and dynamical parameters. As a by-product, we also search for possible yellow straggler stars (YSS), which are believed to be stragglers in a more advanced evolution stage. Methods. We employed photometry, proper motions, and parallaxes extracted from Gaia DR2 for 408 Galactic star clusters and searched for stragglers within them after performing a careful membership analysis. Results. The number of BBS emerging from our more stringent, selection criteria turns out to be significantly smaller than in previous versions of this catalogue. OCs are therefore not a preferable environment for these kinds of stars anymore. In addition, we found that BSS start to appear in clusters with ages larger than log(t) ∼ 8.7 and are therefore absent in very young star clusters. -

ASTRONOMY and ASTROPHYSICS Foreground and Background Dust In
Astron. Astrophys. 359, 347–363 (2000) ASTRONOMY AND ASTROPHYSICS Foreground and background dust in star cluster directions C.M. Dutra1 and E. Bica1 Universidade Federal do Rio Grande do Sul, IF, CP 15051, Porto Alegre 91501–970, RS, Brazil Received 20 January 2000 / Accepted 13 April 2000 Abstract. This paper compares reddening values E(B-V) de- al.’s reddening values (∆E(B-V) = -0.008 and -0.016, respec- rived from the stellar content of 103 old open clusters and 147 tively). The reddening comparisons above hardly exceed the globular clusters of the Milky Way with those derived from limit E(B-V) ≈ 0.30, so that a more extended range should be DIRBE/IRAS 100 µm dust emission in the same directions. explored. Star clusters at |b| > 20◦ show comparable reddening values Since the Galaxy is essentially transparent at 100 µm, the between the two methods, in agreement with the fact that most far-infrared reddening values should represent dust columns of them are located beyond the disk dust layer. For very low integrated throughout the whole Galaxy in a given direction. galactic latitude lines of sight, differences occur in the sense Star clusters probing distances as far as possible throughout that DIRBE/IRAS reddening values can be substantially larger, the Galaxy should be useful to study the dust distribution in suggesting effects due to the depth distribution of the dust. The a given line of sight. Globular clusters and old open clusters differences appear to arise from dust in the background of the are ideal objects for such purposes because they are in general clusters consistent with a dust layer where important extinction distant enough to provide a significant probe of the galactic in- occurs up to distances from the Plane of ≈ 300 pc.