DOCSLIB.ORG

Type of the Paper (Article

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Type of the Paper (Article Supplemental Material Spatiotemporal changes in PM2.5 pollution and the associated mortality burden in China between 2015 and 2016 Luwei Feng 1,a, Bo Ye 2,a, Huan Feng 2, FuRen 1,3,4, Shichun Huang 2, Xiaotong Zhang 2, Yunquan Zhang 2, Qingyun Du 1,3,4,5,* and Lu Ma 2,6,* 1 School of Resources and Environmental Science, Wuhan University, 129 Luoyu Road, Wuhan 430079, China; [email protected] (L.F.); [email protected] (F.R.) 2 Department of Epidemiology and Biostatistics, School of Health Sciences, Wuhan University, 185 Donghu Road, Wuchang District, Wuhan 430071, China; [email protected] (B.Y.); [email protected] (H.F.); [email protected] (S.H.); [email protected] (X.Z.); [email protected] (Y.Z.) 3 Key Laboratory of GIS, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China 4 Key Laboratory of Digital Mapping and Land Information Application Engineering, National Administration of Surveying, Mapping and Geoinformation, Wuhan University, 129 Luoyu Road, Wuhan 430079, China 5 Collaborative Innovation Center of Geospatial Technology, Wuhan University, 129 Luoyu Road, Wuhan 430079, China 6 Global Health Institute, Wuhan University, 8 Donghunan Road, Wuchang District, Wuhan 430072, China * Correspondence: [email protected] (Q.D.); Tel.: + 86-27-8766-4557 (Q.D.); [email protected] (L.M.); Tel.: +86-27-6875-8815 (L.M.) Table of Contents Page Estimates of (α, γ, δ) 2 Estimates of confidence interval for RRIER 2 Table S1 3 Figure S1 4 Figure S2 5 Table S2 5 Reference 12 {rˆ(s) ,...,rˆ (s) ,s = 1,...,S} Estimates of (α, γ, δ): A set of RR estimates 1 Ks and corresponding confidence {z(s) ,...,z (s) ,s = 1,...,S} intervals based on PM2.5 concentrations 1 Ks can be obtained from previous research, where S means different types of PM2.5 sources and Ks is the number of RR estimates available from for source type S. In order to estimate α, δ and γ, flowing steps are needed: First, determine the {rˆ(s) ,...,rˆ (s) ,s = 1,...,S} {γˆ (s),...,γˆ (s) ,s = 1,...,S} logarithm of the relative risk estimates 1 Ks denoted by 1 Ks and then {γˆ (s),...,γˆ (s) ,s = 1,...,S} {νˆ (s),..., νˆ (s) ,s = 1,...,S} denote the standard error of 1 Ks by 1 Ks . After that, generate 1000 realizations of the log-relative risks assuming a normal distribution with mean {γˆ (s),...,γˆ (s) ,s = 1,...,S} {νˆ (s),...,νˆ (s) ,s = 1,...,S} 1 Ks and standard deviation 1 Ks and take their exponents. One thousand estimates of (α, γ, δ) could be obtained for each set of simulated RRs. The estimation routine did not converge in a small percentage of cases (< 5%) due to a set of simulated RR that were not consistent with the risk model form in our practical processing. Thus we continue to simulate relative risks until 1000 estimates of (α, γ, δ) were obtained [1]. Estimates of confidence interval for RRIER: We simulated 1,000 sets of source type–specific RRs based on their point estimates and CIs and fit the IER model to these simulated values, obtaining 1,000 sets of parameter estimates of (α, γ, δ) and zcf. Using these parameters, we then generated Int. J. Environ. Res. Public Health 2017, 14, x; doi: www.mdpi.com/journal/ijerph Int. J. Environ. Res. Public Health 2017, 14, x 2 of 9 1,000 IER values over the global concentration range. The mean of these 1000 IER values at a specific concentration was used as our central estimate of relative risk, and the 2.5% and 97.5% values among the 1000 IER values were used to form the lower and upper confidence intervals for each disease at each specific concentration [1]. Table S1. Change of PM2.5 concentration in provinces from 2015 to 2016. Average change of PM2.5 Number Cities with increasing PM2.5 Cities with decreasing PM2.5 Province from 2015 to 2016 per city of cities b Number Rate (%) Number Rate (%) (μg/m3) a Jilin −9.66 9 0 0 9 100 Hubei −9.05 13 0 0 13 100 Shanghai c −7.62 1 0 0 1 100 Shandong −7.05 17 0 0 17 100 Qinghai −6.81 8 1 12.50 7 87.50 Heilongjiang −6.50 13 1 7.69 12 92.31 Inner Mongolia −6.38 12 1 8.33 11 91.67 Jiangsu −5.84 13 0 0 13 100 Liaoning −5.51 14 1 7.14 13 92.86 Hunan −4.89 14 1 7.14 13 92.86 Zhejiang −4.06 11 1 9.09 10 90.91 Guangxi −3.32 14 2 14.29 12 85.71 Hainan −2.24 2 0 0 2 100 Guangdong −2.15 21 3 14.29 18 85.71 Yunnan −2.11 16 5 31.25 11 68.75 Hebei −2.11 11 4 36.36 7 63.64 Henan −2.05 17 7 41.18 10 58.82 Gansu −1.92 14 4 28.57 10 71.43 Beijing c −1.11 1 0 0 1 100 Fujian −0.85 9 2 22.22 7 77.78 Anhui −0.29 16 6 37.50 10 62.50 Ningxia −0.25 5 2 40 3 60 Guizhou −0.04 9 4 44.44 5 55.56 Chongqing c 0.14 1 1 100 0 0 Sichuan 0.72 21 12 57.14 9 42.86 Tibet 1.10 7 4 57.14 3 42.86 Jiangxi 1.43 11 8 72.73 3 27.27 Tianjin c 2.79 1 1 100 0 0 Shaanxi 4.74 10 5 50 5 50 Shanxi 5.79 11 10 90.91 1 9.09 Xinjiang 7.55 14 8 57.14 6 42.86 SUM −2.34 336 94 27.98 242 72.02 a “+” reflects an increase in PM2.5 from 2015 to 2016, and “−” reflects a decrease in PM2.5 from 2015 to 2016. b Cities without records of PM2.5 are not included. c Shanghai, Beijing, Chongqing and Tianjin are municipalities of China. Int. J. Environ. Res. Public Health 2017, 14, x 3 of 9 Figure S1. Proportion distributions of hourly PM2.5 concentrations (in the range of ≤10 μg/m3 (a), 10–15 μg/m3 (b), 15–25 μg/m3 (c), 25–35 μg/m3 (d), ＞35 μg/m3 (e)) in 336 cities. Int. J. Environ. Res. Public Health 2017, 14, x 4 of 9 Figure S2. Diurnal variation of PM2.5 concentration in four seasons over 2015 and 2016. Table S2. Changes in deaths caused by fluctuations of PM2.5 concentrations from 2015 to 2016 in 336 Chinese cities. City PM2.5 (μg/m3) Change of death number from 2015 to 2016 Province 2015 2016 LC IHD stroke COPD sum Heilongjiang Yichun 26 17 -22.31 -58.16 -219.54 -24.40 -324.41 Heihe 31 22 -18.12 -47.33 -194.99 -19.18 -279.62 Mudanjiang 48 37 -20.06 -35.90 -138.45 -22.60 -217.01 Shuangyashan 42 33 -17.11 -36.44 -125.95 -13.90 -193.41 Hegang 43 34 -17.11 -27.33 -124.41 -18.38 -187.23 Harbin 65 51 -22.04 -42.97 -85.71 -17.37 -168.08 Daxing’anling 25 21 -11.15 -29.08 -105.56 -9.85 -155.64 Qiqihar 49 41 -13.37 -26.73 -91.76 -13.56 -145.42 Daqing 44 38 -13.58 -27.13 -76.09 -9.19 -125.99 Jixi 27 25 -3.69 -9.62 -45.54 -4.88 -63.73 Suihua 37 34 -7.01 -9.25 -40.52 -4.71 -61.49 Qitaihe 37 36 -3.51 -9.25 -10.13 0.00 -22.88 Kiamusze 29 31 3.65 9.54 33.19 4.84 51.22 Jilin Changchun 54 41 -19.16 -29.64 -105.16 -18.63 -172.60 Yanbian 61 46 -18.74 -36.26 -94.92 -18.34 -168.25 Liaoyuan 59 46 -16.18 -29.21 -88.11 -14.79 -148.29 Siping 44 36 -14.23 -30.30 -87.66 -11.55 -143.75 Jilin 58 46 -16.18 -29.21 -81.23 -14.79 -141.41 Songyuan 51 42 -11.12 -22.39 -83.59 -15.03 -132.13 Baicheng 58 48 -13.48 -29.21 -59.07 -11.09 -112.86 Tonghua 36 31 -8.89 -15.62 -76.88 -7.90 -109.28 Baishan 52 50 -2.76 -7.41 -15.11 -3.76 -29.04 Qinghai Haixi 38 27 -16.51 -28.89 -157.66 -36.56 -239.63 Hainan 42 31 -18.81 -28.46 -136.68 -29.01 -212.95 Haibei 39 31 -13.65 -22.94 -107.18 -21.94 -165.71 Haidong 57 46 -12.73 -16.46 -80.45 -27.61 -137.24 Golog 43 37 -8.06 -11.38 -71.47 -21.57 -112.49 Huangnan 51 45 -7.81 -11.13 -52.68 -21.05 -92.67 Yushu 19 17 -6.05 -6.31 -43.15 -7.92 -63.42 Xining 48 50 2.62 5.61 15.32 0.00 23.55 Hubei Xiaogan 71 46 -32.65 -52.76 -141.51 -30.21 -257.14 Jingmen 69 57 -16.44 -30.15 -52.42 -11.42 -110.43 Wuhan 68 57 -16.44 -30.15 -45.18 -11.42 -103.19 Xiangyang 54 47 -11.54 -15.62 -47.51 -11.79 -86.47 Huangshi 66 57 -13.80 -22.77 -37.85 -7.67 -82.10 Jingzhou 69 60 -10.96 -22.61 -37.44 -7.61 -78.63 Suizhou 64 56 -11.12 -15.29 -38.06 -11.51 -75.98 Ezhou 53 47 -8.72 -15.62 -39.82 -7.92 -72.09 Shiyan 52 47 -8.72 -15.62 -39.82 -7.92 -72.09 Huanggang 57 51 -8.59 -15.51 -38.92 -7.79 -70.82 Int.
Load more

Recommended publications
  • Landscape Analysis of Geographical Names in Hubei Province, China
    Entropy 2014, 16, 6313-6337; doi:10.3390/e16126313 OPEN ACCESS entropy ISSN 1099-4300 www.mdpi.com/journal/entropy Article Landscape Analysis of Geographical Names in Hubei Province, China Xixi Chen 1, Tao Hu 1, Fu Ren 1,2,*, Deng Chen 1, Lan Li 1 and Nan Gao 1 1 School of Resource and Environment Science, Wuhan University, Luoyu Road 129, Wuhan 430079, China; E-Mails: [email protected] (X.C.); [email protected] (T.H.); [email protected] (D.C.); [email protected] (L.L.); [email protected] (N.G.) 2 Key Laboratory of Geographical Information System, Ministry of Education, Wuhan University, Luoyu Road 129, Wuhan 430079, China * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel: +86-27-87664557; Fax: +86-27-68778893. External Editor: Hwa-Lung Yu Received: 20 July 2014; in revised form: 31 October 2014 / Accepted: 26 November 2014 / Published: 1 December 2014 Abstract: Hubei Province is the hub of communications in central China, which directly determines its strategic position in the country’s development. Additionally, Hubei Province is well-known for its diverse landforms, including mountains, hills, mounds and plains. This area is called “The Province of Thousand Lakes” due to the abundance of water resources. Geographical names are exclusive names given to physical or anthropogenic geographic entities at specific spatial locations and are important signs by which humans understand natural and human activities. In this study, geographic information systems (GIS) technology is adopted to establish a geodatabase of geographical names with particular characteristics in Hubei Province and extract certain geomorphologic and environmental factors.
    [Show full text]
  • Download Article
    Advances in Economics, Business and Management Research, volume 70 International Conference on Economy, Management and Entrepreneurship（ICOEME 2018) Research on the Path of Deep Fusion and Integration Development of Wuhan and Ezhou Lijiang Zhao Chengxiu Teng School of Public Administration School of Public Administration Zhongnan University of Economics and Law Zhongnan University of Economics and Law Wuhan, China 430073 Wuhan, China 430073 Abstract—The integration development of Wuhan and urban integration of Wuhan and Hubei, rely on and Ezhou is a strategic task in Hubei Province. It is of great undertake Wuhan. Ezhou City takes the initiative to revise significance to enhance the primacy of provincial capital, form the overall urban and rural plan. Ezhou’s transportation a new pattern of productivity allocation, drive the development infrastructure is connected to the traffic artery of Wuhan in of provincial economy and upgrade the competitiveness of an all-around and three-dimensional way. At present, there provincial-level administrative regions. This paper discusses are 3 interconnected expressways including Shanghai- the path of deep integration development of Wuhan and Ezhou Chengdu expressway, Wuhan-Ezhou expressway and from the aspects of history, geography, politics and economy, Wugang expressway. In terms of market access, Wuhan East and puts forward some suggestions on relevant management Lake Development Zone and Ezhou Gedian Development principles and policies. Zone try out market access cooperation, and enterprises Keywords—urban regional cooperation; integration registered in Ezhou can be named with “Wuhan”. development; path III. THE SPACE FOR IMPROVEMENT IN THE INTEGRATION I. INTRODUCTION DEVELOPMENT OF WUHAN AND EZHOU Exploring the path of leapfrog development in inland The degree of integration development of Wuhan and areas is a common issue for the vast areas (that is to say, 500 Ezhou is lower than that of central urban area of Wuhan, and kilometers from the coastline) of China’s hinterland.
    [Show full text]
  • Mapping the Accessibility of Medical Facilities of Wuhan During the COVID-19 Pandemic
    International Journal of Geo-Information Article Mapping the Accessibility of Medical Facilities of Wuhan during the COVID-19 Pandemic Zhenqi Zhou 1, Zhen Xu 1,* , Anqi Liu 1, Shuang Zhou 1, Lan Mu 2 and Xuan Zhang 2 1 Department of Landscape Architecture, College of Landscape Architecture, Nanjing Forestry University, Nanjing 210037, China; [email protected] (Z.Z.); [email protected] (A.L.); [email protected] (S.Z.) 2 Department of Geography, University of Georgia, Athens, GA 30602, USA; [email protected] (L.M.); [email protected] (X.Z.) * Correspondence: [email protected] Abstract: In December 2019, the coronavirus disease 2019 (COVID-19) pandemic attacked Wuhan, China. The city government soon strictly locked down the city, implemented a hierarchical diagnosis and treatment system, and took a series of unprecedented pharmaceutical and non-pharmaceutical measures. The residents’ access to the medical resources and the consequently potential demand– supply tension may determine effective diagnosis and treatment, for which travel distance and time are key indicators. Using the Application Programming Interface (API) of Baidu Map, we estimated the travel distance and time from communities to the medical facilities capable of treating COVID-19 patients, and we identified the service areas of those facilities as well. The results showed significant differences in service areas and potential loading across medical facilities. The accessibility of medical facilities in the peripheral areas was inferior to those in the central areas; there was spatial inequality of medical resources within and across districts; the amount of community healthcare Citation: Zhou, Z.; Xu, Z.; Liu, A.; Zhou, S.; Mu, L.; Zhang, X.
    [Show full text]
  • Environmental Impact Assessment Report
    Environmental Impact Assessment Report For Public Disclosure Authorized Changzhi Sustainable Urban Transport Project E2858 v3 Public Disclosure Authorized Public Disclosure Authorized Shanxi Academy of Environmental Sciences Sept, 2011 Public Disclosure Authorized I TABLE OF CONTENT 1. GENERAL ................................................................ ................................ 1.1 P ROJECT BACKGROUND ..............................................................................................1 1.2 B ASIS FOR ASSESSMENT ..............................................................................................2 1.3 P URPOSE OF ASSESSMENT AND GUIDELINES .................................................................4 1.4 P ROJECT CLASSIFICATION ...........................................................................................5 1.5 A SSESSMENT CLASS AND COVERAGE ..........................................................................6 1.6 I DENTIFICATION OF MAJOR ENVIRONMENTAL ISSUE AND ENVIRONMENTAL FACTORS ......8 1.7 A SSESSMENT FOCUS ...................................................................................................1 1.8 A PPLICABLE ASSESSMENT STANDARD ..........................................................................1 1.9 P OLLUTION CONTROL AND ENVIRONMENTAL PROTECTION TARGETS .............................5 2. ENVIRONMENTAL BASELINE ................................ ................................ 2.1 N ATURAL ENVIRONMENT ............................................................................................3
    [Show full text]
  • Present Status, Driving Forces and Pattern Optimization of Territory in Hubei Province, China Tingke Wu, Man Yuan
    World Academy of Science, Engineering and Technology International Journal of Environmental and Ecological Engineering Vol:13, No:5, 2019 Present Status, Driving Forces and Pattern Optimization of Territory in Hubei Province, China Tingke Wu, Man Yuan market failure [4]. In fact, spatial planning system of China is Abstract—“National Territorial Planning (2016-2030)” was not perfect. It is a crucial problem that land resources have been issued by the State Council of China in 2017. As an important unordered and decentralized developed and overexploited so initiative of putting it into effect, territorial planning at provincial level that ecological space and agricultural space are seriously makes overall arrangement of territorial development, resources and squeezed. In this regard, territorial planning makes crucial environment protection, comprehensive renovation and security system construction. Hubei province, as the pivot of the “Rise of attempt to realize the "Multi-Plan Integration" mode and Central China” national strategy, is now confronted with great contributes to spatial planning system reform. It is also opportunities and challenges in territorial development, protection, conducive to improving land use regulation and enhancing and renovation. Territorial spatial pattern experiences long time territorial spatial governance ability. evolution, influenced by multiple internal and external driving forces. Territorial spatial pattern is the result of land use conversion It is not clear what are the main causes of its formation and what are for a long period. Land use change, as the significant effective ways of optimizing it. By analyzing land use data in 2016, this paper reveals present status of territory in Hubei. Combined with manifestation of human activities’ impact on natural economic and social data and construction information, driving forces ecosystems, has always been a specific field of global climate of territorial spatial pattern are then analyzed.
    [Show full text]
  • Chinacoalchem
    ChinaCoalChem Monthly Report Issue May. 2019 Copyright 2019 All Rights Reserved. ChinaCoalChem Issue May. 2019 Table of Contents Insight China ................................................................................................................... 4 To analyze the competitive advantages of various material routes for fuel ethanol from six dimensions .............................................................................................................. 4 Could fuel ethanol meet the demand of 10MT in 2020? 6MTA total capacity is closely promoted ....................................................................................................................... 6 Development of China's polybutene industry ............................................................... 7 Policies & Markets ......................................................................................................... 9 Comprehensive Analysis of the Latest Policy Trends in Fuel Ethanol and Ethanol Gasoline ........................................................................................................................ 9 Companies & Projects ................................................................................................... 9 Baofeng Energy Succeeded in SEC A-Stock Listing ................................................... 9 BG Ordos Started Field Construction of 4bnm3/a SNG Project ................................ 10 Datang Duolun Project Created New Monthly Methanol Output Record in Apr ........ 10 Danhua to Acquire &
    [Show full text]
  • Environmental Impact Assessment Executive Summary
    SFG3333 REV Public Disclosure Authorized Environmental Impact Assessment Executive Summary For Public Disclosure Authorized Shanxi Gas Utilization Project - Yangcheng Gas Utilization Subproject (Draft) Public Disclosure Authorized Public Disclosure Authorized Coal Chemistry Institute of China Academy of Sciences Mar. 2017 EXECUTIVE SUMMARY Shanxi Gas Utilization Project – Yangcheng Gas Utilization Subproject TABLE OF CONTENT 1. INTRODUCTION ................................................................................................................3 1.1 PROJECT BACKGROUND ---------------------------------------------------------------------------------------- 3 1.2 ENVIRONMENTAL POLICIES, LAWS AND REGULATIONS --------------------------------------------------- 3 1.2.1 Laws and Regulations ...................................................................................................................... 3 1.2.2 Safeguard Policies and EHS Guideline ........................................................................................... 3 1.2.3 Applicable Standards ....................................................................................................................... 4 2. PROJECT DESCRIPTION .................................................................................................4 2.1 PROJECT COMPOSITION ----------------------------------------------------------------------------------------- 4 2.2 GAS CONSUMPTION ---------------------------------------------------------------------------------------------
    [Show full text]
  • Evaluating the Influence of Land Use and Land Cover Change on Fine
    www.nature.com/scientificreports OPEN Evaluating the infuence of land use and land cover change on fne particulate matter Wei Yang1* & Xiaoli Jiang2 Fine particulate matter (i.e. particles with diameters smaller than 2.5 microns, PM2.5) has become a critical environmental issue in China. Land use and land cover (LULC) is recognized as one of the most important infuence factors, however very fewer investigations have focused on the impact of LULC on PM2.5. The infuences of diferent LULC types and diferent land use and land cover change (LULCC) types on PM2.5 are discussed. A geographically weighted regression model is used for the general analysis, and a spatial analysis method based on the geographic information system is used for a detailed analysis. The results show that LULCC has a stable infuence on PM2.5 concentration. For diferent LULC types, construction lands have the highest PM2.5 concentration and woodlands have the lowest. The order of PM2.5 concentration for the diferent LULC types is: construction lands > unused lands > water > farmlands >grasslands > woodlands. For diferent LULCC types, when high-grade land types are converted to low-grade types, the PM2.5 concentration decreases; otherwise, the PM2.5 concentration increases. The result of this study can provide a decision basis for regional environmental protection and regional ecological security agencies. With the rapid development of China’s economy and society, its rate of urbanization is accelerating. China’s industrial scale is also expanding rapidly, and the problem of air pollution is becoming increasingly serious, which has a tremendous impact on the environment, economic development, and even people’s health 1.
    [Show full text]
  • Here You Can Taste Wuhan Featured Food
    Contents Basic Mandarin Chinese Words and Phrases............................................... 2 Useful Sayings....................................................................................... 2 In Restaurants....................................................................................... 3 Numbers................................................................................................3 Dinning and cafes..........................................................................................5 Eating Out in Wuhan.............................................................................5 List of Restaurants and Food Streets (sort by distance).......................6 4 Places Where You Can Taste Wuhan Featured Food.........................7 Restaurants and cafes in Walking Distance........................................11 1 Basic Mandarin Chinese Words and Phrases Useful Sayings nǐ hǎo Hello 你 好 knee how zài jiàn Goodbye 再 见 zi gee’en xiè xiè Thank You 谢 谢！ sheh sheh bú yòng le, xiè xiè No, thanks. 不 用 了，谢 谢 boo yong la, sheh sheh bú yòng xiè You are welcome. 不 用 谢 boo yong sheh wǒ jiào… My name is… 我 叫… wore jeow… shì Yes 是 shr bú shì No 不 是 boo shr hǎo Good 好 how bù hǎo Bad 不 好 boo how duì bù qǐ Excuse Me 对 不 起 dway boo chee wǒ tīng bù dǒng I do not understand 我 听 不 懂 wore ting boo dong duō shǎo qián How much? 多 少 钱? dor sheow chen Where is the xǐ shǒu jiān zài nǎ lǐ See-sow-jian zai na-lee washroom? 洗 手 间 在 哪 里 2 In Restaurants In China, many people call a male waiter as handsome guy and a female waitress as beautiful girl. It is also common to call “fú wù yuan” for waiters of both genders. cài dān Menu 菜 单 tsai dan shuài gē Waiter(Handsome) 帅 哥 shuai ge měi nǚ Waitress(Beautiful) 美 女 may nyu fú wù yuán Waiter/Waitress 服 务 员 fu woo yuan wǒ xiǎng yào zhè ge 我 I would like this.
    [Show full text]
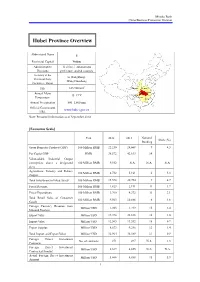
  • Hubei Province Overview
    Mizuho Bank China Business Promotion Division Hubei Province Overview Abbreviated Name E Provincial Capital Wuhan Administrative 12 cities, 1 autonomous Divisions prefecture, and 64 counties Secretary of the Li Hongzhong; Provincial Party Wang Guosheng Committee; Mayor 2 Size 185,900 km Shaanxi Henan Annual Mean Hubei Anhui 15–17°C Chongqing Temperature Hunan Jiangxi Annual Precipitation 800–1,600 mm Official Government www.hubei.gov.cn URL Note: Personnel information as of September 2014 [Economic Scale] Unit 2012 2013 National Share (%) Ranking Gross Domestic Product (GDP) 100 Million RMB 22,250 24,668 9 4.3 Per Capita GDP RMB 38,572 42,613 14 - Value-added Industrial Output (enterprises above a designated 100 Million RMB 9,552 N.A. N.A. N.A. size) Agriculture, Forestry and Fishery 100 Million RMB 4,732 5,161 6 5.3 Output Total Investment in Fixed Assets 100 Million RMB 15,578 20,754 9 4.7 Fiscal Revenue 100 Million RMB 1,823 2,191 11 1.7 Fiscal Expenditure 100 Million RMB 3,760 4,372 11 3.1 Total Retail Sales of Consumer 100 Million RMB 9,563 10,886 6 4.6 Goods Foreign Currency Revenue from Million USD 1,203 1,219 15 2.4 Inbound Tourism Export Value Million USD 19,398 22,838 16 1.0 Import Value Million USD 12,565 13,552 18 0.7 Export Surplus Million USD 6,833 9,286 12 1.4 Total Import and Export Value Million USD 31,964 36,389 17 0.9 Foreign Direct Investment No.
    [Show full text]
  • Ill-Health and Ill Treatment of Gong Shengliang
    AI Index: ASA 17/008/2005 Distrib: PG/SC To: Health Professionals From: Health and Human Rights Team Date: 17 March 2005 MEDICAL ACTION CHINA: Ill-health and ill treatment of Gong Shengliang Amnesty International (AI) is seriously concerned for the life and well being of Gong Shengliang, a Protestant pastor and leader of the banned "Huanan (South China) Church", who is imprisoned in Hongshan prison, Hubei Province. Gong Shengliang's latest health setbacks are compounded by the continual ill-treatment he has received since his imprisonment in 2001. During his imprisonment, Gong Shengliang has suffered continual ill-treatment. According to letters that he wrote in the first two weeks of December 2004, which have only recently been published on the internet, Gong Shengliang describes how he was suffering from a debilitating stomach complaint, and how he had been able to only take a little food and water for at least 11 days. Gong Shengliang had been treated at the prison hospital five times and on 6 December 2004 asked to be admitted to a hospital outside the prison. However, this request was refused by the prison authorities, who, on one occasion, threatened Gong Shengliang with what were described as "heavy-handed measures". The prison authorities later agreed to Gong Shengliang’s request and he then received treatment at a provincial hospital and an army hospital, following which he was diagnosed with a duodenal ulcer. Throughout this time, Gong Shengliang had been refused visits from his family. Background information Gong Shengliang
    [Show full text]
  • Infection in Wuhan, China
    DR. WEI GUO (Orcid ID : 0000-0001-8686-3779) Article type : Letter to the Editor Patterns of HIV and SARS-CoV-2 co-infection in Wuhan, China Wei Guo1,2*, Fangzhao Ming3*, Yong Feng4*, Qian Zhang5, Pingzhen Mo6, Lian Liu7, Ming Gao8, Weiming Tang9§ and Ke Liang6§ 1. Department of Pathology, Zhongnan Hospital of Wuhan University, Wuhan, China 2. Department of Pathology, School of Basic Medical Sciences, Wuhan University, Wuhan, China 3. Wuchang District Center for Disease Control and Prevention,Wuhan, China 4. State Key Laboratory of Virology/Department of Medical Microbiology, School of Basic Medical Sciences, Wuhan University, Wuhan, China 5. Qingshan District Center for Disease Control and Prevention,Wuhan, China 6. Department of Infectious Diseases, Zhongnan Hospital of Wuhan University, Wuhan University, Hubei, China 7. Caidian District Center for Disease Control and Prevention, Wuhan, China 8. Xinzhou District Center for Disease Control and Prevention, Wuhan, China 9. Dermatology Hospital, Southern Medical University, and the University of North Carolina at Chapel Hill Project-China, Guangzhou, China * These authors equally contributed to this manuscript and are co-first authors. This article has been accepted for publication and undergone full peer review but has not been through the copyediting, typesetting, pagination and proofreading process, which may lead to differencesAccepted Article between this version and the Version of Record. Please cite this article as doi: 10.1002/jia2.25568 This article is protected by copyright. All rights reserved § These authors contributed equally. Correspondence to: Dr. Ke Liang, Department of Infectious Diseases Zhongnan Hospital in Wuhan University, Wuhan, 430071, China; Email: [email protected] Keywords: Clinical patterns; HIV; SARS-CoV-2; Co-infection; COVID-19; CD4+ T lymphocyte count; lymphopenia Accepted Article This article is protected by copyright.
    [Show full text]