DOCSLIB.ORG

Butterworth Filter

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Butterworth Filter Butterworth Filter Spring 2012 © Ammar Abu-Hudrouss -Islamic ١ University Gaza Filter types What are the function of Filters ? A filter is a system that allow certain frequency to pass to its output and reject all other signals Filters can be classified according to range of signal frequencies in the passband Lowpass filter Highpass filter Bandpass filter Stopband (bandreject) filter Digital Signal Processing ٢ Slide ١ Filter types Digital Signal Processing ٣ Slide Filter types Filter types according to its frequency response Butterworth filter Chebychev I filter Chebychev II filter Elliptic filter Digital Signal Processing ٤ Slide ٢ Butterworth filter Ideal lowpass filter is shown in the figure The passband is normalised to one. Tolerance in passband and stopband are allowed to enable the construction of the filter. Digital Signal Processing ٥ Slide Lowpass prototype filter Lowpass prototype filter: it is a lowpass filter with cutoff frequency p =1. The frequency scale is normalized by p. We use = / p. Lowpass filter Highpass filter Lowpass Frequency prototype Transformation filter Bandpass filter Bandreject filter Digital Signal Processing ٦ Slide ٣ Lowpass prototype filter Notation In analogue filter design we will use s to denote complex frequency to denote analogue frequency p to denote complex frequency at lowpass prototype frequencies. to denote analogue frequency at the lowpass prototype frequencies. Digital Signal Processing ٧ Slide Magnitude Approximation of Analog Filters The transfer function of analogue filter is given as rational function of the form 2 m co c1s c2s cms Hs 2 n m n d0 d1s d2s dn s The Fourier transform is given by 2 m m co jc1 c2 j cm H H (s) s j 2 n n d0 jd1 d2 j dn H H ( j) e j Digital Signal Processing ٨ Slide ٤ Magnitude Approximation of Analog Filters Analogue filter is usually expressed in term of H j 2 H jH * j H j 2 H j Example Consider the transfer function of analogue filter, find s 1 H s s2 2s 2 2 s 1 s 1 H j H sH s s j s 2 2s 2 s 2 2s 2 s j 2 2 1 H j 4 4 Digital Signal Processing ٩ Slide Butterworth filter 2 H j will have only even powers of , or 2 4 2m 2 Co C2 C4 C2m H () 2 4 2n 1 D2 D4 D2n In order to approximate the ideal filter 1) The magnitude at = 0 is normalized to one 2) The magnitude monotonically decreases from this value to zero as ∞. 3) The maximum number of its derivatives evaluated at = 0 are zeros. 2 1 H () This can be satisfied if 2N 1 D2N Digital Signal Processing ١٠ Slide ٥ Butterworth filter The following specification is usually given for a lowpass Butterworth filter is 1) The magnitude of H0 at = 0 2) The bandwidth p. 3) The magnitude (-Ap dB) at the bandwidth p. 4) The stopband frequency s. 5) The magnitude (-As dB) at the stopband frequency s . 6) The transfer function is given by 2 H0 H() 2N 1D2N Digital Signal Processing ١١ Slide Butterworth filter To achieve the equivalent lowpass prototype filter 1) We scale the cutoff frequency to one using transformation = / p. 2) We scale the max. magnitude to 1 to one by dividing the magnitude by H0 . The transfer function become 2 1 H() ' 2N 1 D2N 2 We denotes D’2N as where is the ripple factor, then 2 1 H() 1 2 2N Digital Signal Processing ١٢ Slide ٦ Butterworth filter 2 If the magnitude at the bandwidth = p = 1 is given as (1 - p) or −Ap decibels, the value of 2 is computed by 2 10log H () Ap p 1 1 10log A 1 2 p 2 100.1Ap 1 2 If we choose Ap = -3dB = 1. this is the most common case and gives 2 1 H () 1 2 N Digital Signal Processing ١٣ Slide Butterworth filter If we use the complex frequency representation 2 2 1 H( p) H p / j N 1 p 2 The poles of this function occurs at e 2 jk / 2 N k 1,2,..., 2N , n even p k 2k 1 j / 2 N e k 1,2,..., 2N , n odd Or in general j(2k N 1) / 2N pk e k 1,2,...,2N Poles occurs in complex conjugates Poles which are located in the LHP are the poles of H (s) j(2k N1) /2N pk e k 1,2,..., N Digital Signal Processing ١٤ Slide ٧ Butterworth filter When we found the N poles we can construct the filter transfer function as 1 H p Dp The denominator polynomial D (p) is calculated by n Dp p pk k 1 Digital Signal Processing ١٥ Slide Butterworth filter Another method to calculate D (p ) using D( p) p pk k 2 n D( p) 1 d1 p d2 p dn p cosk 1 / 2 d d k 1,2,3,, N k k k1 sin 2N The coefficients dk is calculated recursively where d0 = 1 Digital Signal Processing ١٦ Slide ٨ Butterworth filter The minimum attenuation as dB is usually given at certain frequency s. The order of the filter can be calculated from the filter equation 2 10log H (s ) As 10log 1 2 N s H() dB log10As /10 1 N 2logs Digital Signal Processing (rad/sec) s ١٧ Slide Design Steps of Butterworth Filter 1. Convert the filter specifications to their equivalents in the lowpass prototype frequency. 2. From Ap determine the ripple factor . 3. From As determine the filter order, N. 4. Determine the left-hand poles, using the equations given. 5. Construct the lowpass prototype filter transfer function. 6. Use the frequency transformation to convert the LP prototype filter to the given specifications. Digital Signal Processing ١٨ Slide ٩ Butterworth filter Example: Design a lowpass Butterworth filter with a maximum gain of 5 dB and a cutoff frequency of 1000 rad/s at which the gain is at least 2 dB and a stopband frequency of 5000 rad/s at which the magnitude is required to be less than −25dB. Solution: p = 1000 rad/s , s = 5000 rad/s, By normalization, p = p/ p = 1 rad/s, s = s / p = 5 rad/s, And the stopband attenuation As = 25+ 5 =30 dB The filter order is calculated by log(10 As /10 1) N 2.146 3 2log(5) Digital Signal Processing ١٩ Slide Butterworth filter The pole positions are: j2k2 /6 pk e k 1,2,3 j2 /3 j j4 /3 pk e ,e ,e 0.5 j0.866,1,0.5 j0.866 D( p) p 0.5 j0.866p 1p 0.5 j0.866 D( p) p 2 p 1p 1 D( p) p3 2 p 2 2 p 1 Hence the transfer function of the normalized prototype filter of third order is 1 H ( p) p3 2 p2 2 p 1 Digital Signal Processing ٢٠ Slide ١٠ Butterworth filter To restore the magnitude, we multiply be H0 H H ( p) 0 p3 2 p2 2 p 1 20logH0 = 5dB which leads H0 = 1.7783 To restore the frequency we replace p by s/1000 1.7783 H (s) H p ps /1000 3 2 s s s 2 2 1 1000 1000 1000 1.7783.109 H (s) s3 2000s2 2106 s 109 Digital Signal Processing ٢١ Slide Butterworth filter If the passband edge is defined for Ap 3 dB (i.e. 1). The design equation needs to be modified. The formula for calculating the order will become A /10 log 10As /10 1 10 p 1 N 2logs And the poles are given by 1/ N j(2kN 1) / 2N pk e k 1,2,...,N Home Study: Repeat the previous example if Ap = 0.5 dB Digital Signal Processing ٢٢ Slide ١١.
Load more

Recommended publications
  • Emotion Perception and Recognition: an Exploration of Cultural Differences and Similarities
    Emotion Perception and Recognition: An Exploration of Cultural Differences and Similarities Vladimir Kurbalija Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Mirjana Ivanović Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Miloš Radovanović Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Zoltan Geler Department of Media Studies, Faculty of Philosophy, University of Novi Sad dr Zorana Đinđića 2, 21000 Novi Sad, Serbia +381 21 4853918, [email protected] Weihui Dai School of Management, Fudan University Shanghai 200433, China [email protected] Weidong Zhao School of Software, Fudan University Shanghai 200433, China [email protected] Corresponding author: Vladimir Kurbalija, tel. +381 64 1810104 ABSTRACT The electroencephalogram (EEG) is a powerful method for investigation of different cognitive processes. Recently, EEG analysis became very popular and important, with classification of these signals standing out as one of the mostly used methodologies. Emotion recognition is one of the most challenging tasks in EEG analysis since not much is known about the representation of different emotions in EEG signals. In addition, inducing of desired emotion is by itself difficult, since various individuals react differently to external stimuli (audio, video, etc.). In this article, we explore the task of emotion recognition from EEG signals using distance-based time-series classification techniques, involving different individuals exposed to audio stimuli.
    [Show full text]
  • Active Control of Loudspeakers: an Investigation of Practical Applications
    Downloaded from orbit.dtu.dk on: Dec 18, 2017 Active control of loudspeakers: An investigation of practical applications Bright, Andrew Paddock; Jacobsen, Finn; Polack, Jean-Dominique; Rasmussen, Karsten Bo Publication date: 2002 Document Version Early version, also known as pre-print Link back to DTU Orbit Citation (APA): Bright, A. P., Jacobsen, F., Polack, J-D., & Rasmussen, K. B. (2002). Active control of loudspeakers: An investigation of practical applications. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Active Control of Loudspeakers: An Investigation of Practical Applications Andrew Bright Ørsted·DTU – Acoustic Technology Technical University of Denmark Published by: Ørsted·DTU, Acoustic Technology, Technical University of Denmark, Building 352, DK-2800 Kgs. Lyngby, Denmark, 2002 3 This work is dedicated to the memory of Betty Taliaferro Lawton Paddock Hunt (1916-1999) and to Samuel Raymond Bright, Jr. (1936-2001) 4 5 Table of Contents Preface 9 Summary 11 Resumé 13 Conventions, notation, and abbreviations 15 Conventions......................................................................................................................................
    [Show full text]
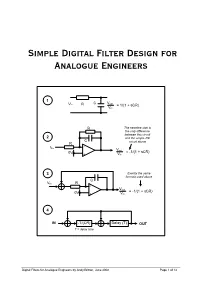
  • Simple Simple Digital Filter Design for Analogue Engineers
    Simple Digital Filter Design for Analogue Engineers 1 C Vout Vin R = 1/(1 + sCR) Vin R The negative sign is the only difference between this circuit 2 and the simple RC C R circuit above - Vin Vout 0V = -1/(1 + sCR) + Vin 3 Exactly the same formula used above C Vin R - Vout 0V = -1/(1 + sCR) + Vin 4 IN -T/(CR) Delay (T) OUT T = delay time Digital Filters for Analogue Engineers by Andy Britton, June 2008 Page 1 of 14 Introduction If I’d read this document years ago it would have saved me countless hours of agony and confusion understanding what should be conceptually very simple. My biggest discontent with topical literature is that they never cleanly relate digital filters to “real world” analogue filters. This article/document sets out to: - • Describe the function of a very basic RC low pass analogue filter • Convert this filter to an analogue circuit that is digitally realizable • Explain how analogue functions are converted to digital functions • Develop a basic 1st order digital low-pass filter • Develop a 2nd order filter with independent Q and frequency control parameters • Show how digital filters can be proven/designed using a spreadsheet such as excel • Demonstrate digital filters by showing excel graphs of signals • Explain the limitations of use of digital filters i.e. when they become unstable • Show how these filters fit in to the general theory (yawn!) Before the end of this article you should hopefully find something useful to guide you on future designs and allow you to successfully implement a digital filter.
    [Show full text]
  • Simulating the Directivity Behavior of Loudspeakers with Crossover Filters
    Audio Engineering Society Convention Paper Presented at the 123rd Convention 2007 October 5–8 New York, NY, USA The papers at this Convention have been selected on the basis of a submitted abstract and extended precis that have been peer reviewed by at least two qualified anonymous reviewers. This convention paper has been reproduced from the author's advance manuscript, without editing, corrections, or consideration by the Review Board. The AES takes no responsibility for the contents. Additional papers may be obtained by sending request and remittance to Audio Engineering Society, 60 East 42nd Street, New York, New York 10165-2520, USA; also see www.aes.org. All rights reserved. Reproduction of this paper, or any portion thereof, is not permitted without direct permission from the Journal of the Audio Engineering Society. Simulating the Directivity Behavior of Loudspeakers with Crossover Filters Stefan Feistel1, Wolfgang Ahnert2, and Charles Hughes3, and Bruce Olson4 1 Ahnert Feistel Media Group, Arkonastr.45-49, 13189 Berlin, Germany [email protected] 2 Ahnert Feistel Media Group, Arkonastr.45-49, 13189 Berlin, Germany [email protected] 3 Excelsior Audio Design & Services, LLC, Gastonia, NC, USA [email protected] 4 Olson Sound Design, Brooklyn Park, MN, USA [email protected] ABSTRACT In previous publications the description of loudspeakers was introduced based on high-resolution data, comprising most importantly of complex directivity data for individual drivers as well as of crossover filters. In this work it is presented how this concept can be exploited to predict the directivity balloon of multi-way loudspeakers depending on the chosen crossover filters.
    [Show full text]
  • Framsida Msc Thesis Viktor Gunnarsson
    Assessment of Nonlinearities in Loudspeakers Volume dependent equalization Master’s Thesis in the Master’s programme in Sound and Vibration VIKTOR GUNNARSSON Department of Civil and Environmental Engineering Division of Applied Acoustics Chalmers Room Acoustics Group CHALMERS UNIVERSITY OF TECHNOLOGY Göteborg, Sweden 2010 Master’s Thesis 2010:27 MASTER’S THESIS 2010:27 Assessment of Nonlinearities in Loudspeakers Volume dependent equalization VIKTOR GUNNARSSON Department of Civil and Environmental Engineering Division of Applied Acoustics Roomacoustics Group CHALMERS UNIVERSITY OF TECHNOLOGY Goteborg,¨ Sweden 2010 CHALMERS, Master’s Thesis 2010:27 ii Assessment of Nonlinearities in Loudspeakers Volume dependent equalization © VIKTOR GUNNARSSON, 2010 Master’s Thesis 2010:27 Department of Civil and Environmental Engineering Division of Applied Acoustics Roomacoustics Group Chalmers University of Technology SE-41296 Goteborg¨ Sweden Tel. +46-(0)31 772 1000 Reproservice / Department of Civil and Environmental Engineering Goteborg,¨ Sweden 2010 Assessment of Nonlinearities in Loudspeakers Volume dependent equalization Master’s Thesis in the Master’s programme in Sound and Vibration VIKTOR GUNNARSSON Department of Civil and Environmental Engineering Division of Applied Acoustics Roomacoustics Group Chalmers University of Technology Abstract Digital room correction of loudspeakers has become popular over the latest years, yield- ing great gains in sound quality in applications ranging from home cinemas and cars to audiophile HiFi-systems. However,
    [Show full text]
  • T/HIS 15.0 User Manual
    For help and support from Oasys Ltd please contact: UK The Arup Campus Blythe Valley Park Solihull B90 8AE United Kingdom Tel: +44 121 213 3399 Email: [email protected] China Arup 39/F-41/F Huaihai Plaza 1045 Huaihai Road (M) Xuhui District Shanghai 200031 China Tel: +86 21 3118 8875 Email: [email protected] India Arup Ananth Info Park Hi-Tec City Madhapur Phase-II Hyderabad 500 081, Telangana India Tel: +91 40 44369797 / 98 Email: [email protected] Web:www.arup.com/dyna or contact your local Oasys Ltd distributor. LS-DYNA, LS-OPT and LS-PrePost are registered trademarks of Livermore Software Technology Corporation User manual Version 15.0, May 2018 T/HIS 0 Preamble 0.1 Text conventions used in this manual 0.1 1 Introduction 1.1 1.1 Program Limits 1.1 1.2 Running T/HIS 1.2 1.3 Command Line Options 1.4 2 Using Screen Menus 2.1 2.1 Basic screen menu layout 2.1 2.2 Mouse and keyboard usage for screen-menu interface 2.2 2.3 Dialogue input in the screen menu interface 2.4 2.4 Window management in the screen interface 2.4 2.5 Dynamic Viewing (Using the mouse to change views). 2.5 2.6 "Tool Bar" Options 2.6 3 Graphs and Pages 3.1 3.1 Creating Graphs 3.1 3.2 Page Size 3.2 3.3 Page Layouts 3.2 3.3.1 Automatic Page Layout 3.2 3.4 Pages 3.6 3.5 Active Graphs 3.6 4 Global Commands and Pages 4.1 4.1 Page Number 4.1 4.2 PLOT (PL) 4.1 4.3 POINT (PT) 4.2 4.4 CLEAR (CL) 4.2 4.5 ZOOM (ZM) 4.2 4.6 AUTOSCALE (AU) 4.2 4.7 CENTRE (CE) 4.2 4.8 MANUAL 4.2 4.9 STOP 4.2 4.10 TIDY 4.2 4.11 Additional Commands 4.3 5 Main Menu 5.1 5.0 Selecting Curves
    [Show full text]
  • Classic Filters There Are 4 Classic Analogue Filter Types: Butterworth, Chebyshev, Elliptic and Bessel. There Is No Ideal Filter
    Classic Filters There are 4 classic analogue filter types: Butterworth, Chebyshev, Elliptic and Bessel. There is no ideal filter; each filter is good in some areas but poor in others. • Butterworth: Flattest pass-band but a poor roll-off rate. • Chebyshev: Some pass-band ripple but a better (steeper) roll-off rate. • Elliptic: Some pass- and stop-band ripple but with the steepest roll-off rate. • Bessel: Worst roll-off rate of all four filters but the best phase response. Filters with a poor phase response will react poorly to a change in signal level. Butterworth The first, and probably best-known filter approximation is the Butterworth or maximally-flat response. It exhibits a nearly flat passband with no ripple. The rolloff is smooth and monotonic, with a low-pass or high- pass rolloff rate of 20 dB/decade (6 dB/octave) for every pole. Thus, a 5th-order Butterworth low-pass filter would have an attenuation rate of 100 dB for every factor of ten increase in frequency beyond the cutoff frequency. It has a reasonably good phase response. Figure 1 Butterworth Filter Chebyshev The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. Chebyshev filters where the ripple is only allowed in the passband are called type 1 filters. Chebyshev filters that have ripple only in the stopband are called type 2 filters , but are are seldom used.
    [Show full text]
  • Comparison of a Low-Frequency Butterworth Filter with a Symmetric SE-Filter
    Comparison of a low-frequency Butterworth filter with a symmetric SE-filter K S Medvedeva1 1Saratov State University, Astrakhanskaya Street 83, Saratov, Russia, 410012 Abstract. The article compares two filters: a Butterworth filter and an asymmetric SE- filter.The experimental studydetermines their advantages and disadvantages.Also,experiments based on the peak signal-to-noise ratio(PSNR) metricshowvisual evaluation. The results of experimentsshow that a symmetric filter better restores images usinga small set of continuous function parametersthatare distorted by a low-frequency Gaussian filter. 1. Introduction Due to the imperfection of forming and recording systems, images recorded by systemsare distorted (fuzzy) copiesof the original images. The main causes of distortions that resultindegradation of clarity includethe limited resolution of the forming system, refocusing, the presence of a distorting medium (for example, the atmosphere), and movement of the camera on the object being registered. Eliminating or reducing distortion for clarity is the task of image recovery. Automatic control systems, measuring equipment, signal processing systems, and various filters with different characteristics are used to filter signalsin telecommunications. Depending on the frequency band associated with the bandwidth and the suppression band, there are odd, band, high- frequency, and low-frequency filters. Also, all-pass filters have a constant amplitude-frequency response in the required frequency range, and their phase-frequency response is a given frequency function [1]. The simplest way to restoreimage clarity is to process the observed image in the spatial frequency domain with an inverse filter [2].The drawbacks of this filter are the occurrence of edge effects, which take the form of an oscillating hindrance of high power that completely masksthe reconstructed image.
    [Show full text]
  • Introduction to Signals & Systems
    A very Brief Introduction to Signals & Systems Outline • Signals & Systems • Continuous and discrete time signals • Properties of Systems • Input- Output relation : Convolution • Frequency domain representation of signals & systems • Analog to digital Conversion • Sampling – Nyquist Sampling Theorem • Basic Filter Theory • Types of filters • Designing practical filters in Labview and Matlab • What is a signal? – A signal is a function defined on the continuum of time values • What is a system ? – a system is a black box that “takes in” one or more input signals and “produces” one or more output signals Continuous time Vs Discrete time Signals • Most of the modern day systems are discrete time systems. E.g., A computer. • A computer can’t directly process a continuous time signal but instead it needs a stream of numbers, which is a discrete time signal. • Discrete time signals are obtain by sampling the continuous time signals • How fast should we sample the signal? Examples • Signals – Unit Step function – Continuous time impulse function – Discrete time • Systems – A simple circuit Basic System Properties • Linearity – System is linear if the principle of superposition holds • Time- Invariance – The system does not change with time Convolution • Linear & Time invariant (LTI) sytems are characterized by their impulse response • Impulse response is the output of the system when the input to the system is an impulse function • For Continuous time signals • For Discrete time signals Frequency domain representation of signals • In most of
    [Show full text]
  • A New Digital Filter Using Window Resizing for Protective Relay Applications
    A New Digital Filter Using Window Resizing for Protective Relay Applications Bogdan Kasztenny, Mangapathirao V. Mynam, Titiksha Joshi, and Chad Daniels Schweitzer Engineering Laboratories, Inc. Published in the proceedings of the 15th International Conference on Developments in Power System Protection Liverpool, United Kingdom March 9–12, 2020 A NEW DIGITAL FILTER USING WINDOW RESIZING FOR PROTECTIVE RELAY APPLICATIONS Bogdan Kasztenny1*, Mangapathirao V. Mynam1, Titiksha Joshi1, Chad Daniels1 1Schweitzer Engineering Laboratories, Inc., Pullman, Washington, USA *[email protected] Keywords: POWER SYSTEM PROTECTION, VARIABLE-WINDOW FILTER, WINDOW RESIZING. Abstract Digital protective relays use finite impulse response filters with sliding data windows for band-pass filtering of voltages and currents and measurement of phasors. Cosine, Fourier, and Walsh data windows are commonly used. Short windows yield faster protection operation but allow larger transient errors jeopardizing protection security and calling for adequate countermeasures. Often, these countermeasures erase some, if not most, benefits of shorter data windows. This paper presents the theory, implementation, laboratory test results, and a field case example of a new filtering method for protective relaying based on window resizing. The method uses a full-cycle sliding data window until a disturbance is detected, at which time the window size is considerably shortened to include only disturbance samples and exclude all pre-disturbance samples. With passing of time, the window size grows to include more disturbance samples as they become available. When the window reaches its nominal full-cycle size, it stops extending and starts sliding again. By purging the pre-disturbance data, the new filter strikes an excellent balance between speed and accuracy.
    [Show full text]
  • Butterworth Filter
    Experiment / Circuit Simulation 0 Butterworth Filters All pages have been marked “for evaluation only” to prevent unauthorized use while still allowing customers to evaluate them for suitability in their courses. Your patience in recognizing this necessity is sincerely appreciated. All stamps are removed before your custom manual is paginated and printed. Objectives © 2002, Formulations Media Inc. 1. To use basic filter circuits to design multi-order filter response. 2. To recognize the interchangeability of components to alter design and create high pass or low pass filters. 3. To apply Butterworth polynomial coefficients in the design of filters. 4. To control operational amplifier gain in filter circuits where the gain is often critical to proper design. 5. To cascade filters to create different characteristics than exist with the individual filters. 6. To simulate various multi-order filters using Electronics Workbench™ software running in a Macintosh™ or Windows™ environment, or other similar software. Equipment 8 Resistors: 680 W (2), 3.3 kW (2), 5.6 kW (2), 68 kW (2) 4 Capacitors: 47 nF (4) 2 LM741 Operational Amplifiers Information There are a number of different multi-order filter circuit configurations, one of which is Butterworth. Amulti-order filter is one which has slope rates exceeding ±20 dB/decade. Athird order filter, for example, will have a slope rate of ±60 dB/decade. At the filter break frequency or critical frequency, fc, the filter response may be peaked or attenuated, depending on the circuit damping factor, zeta (z). The effects of z will not be considered in this experiment as z will be set to 0.707, thus providing -3 dB response at the critical frequency.
    [Show full text]
  • Low Pass Filter Prototype – Maximally Flat
    EKT 441 MICROWAVE COMMUNICATIONS MICROWAVE FILTERS 1 INTRODUCTIONWhat is a Microwave filter ? Circuit that controls the frequency response at a certain point in a microwave system provides perfect transmission of signal for frequencies in a certain passband region infinite attenuation for frequencies in the stopband region Attenuation/dB Attenuation/dB 0 0 3 3 10 10 20 20 30 30 40 40 1 2 c 2 FILTER DESIGN METHODS Filter Design Methods Two types of commonly used design methods: - Image Parameter Method - Insertion Loss Method •Image parameter method yields a usable filter Filters designed using the image parameter method consist of a cascade of simpler two port filter sections to provide the desired cutoff frequencies and attenuation characteristics but do not allow the specification of a particular frequency response over the complete operating range. Thus, although the procedure is relatively simple, the design of filters by the image parameter method often must be iterated many times to achieve the desired results. 3 Filter Design by The Insertion Loss Method The perfect filter would have zero insertion loss in the pass- band, infinite attenuation in the stop-band, and a linear phase response in the pass-band. 4 Filter Design by The Insertion Loss Method 5 Filter Design by The Insertion Loss Method 6 Filter Design by The Insertion Loss Method 7 Filter Design by The Insertion Loss Method Practical filter response: Maximally flat: • also called the binomial or Butterworth response, • is optimum in the sense that it provides the flattest possible passband response for a given filter complexity. N 2 PLR 1 k c Equal ripple also known as Chebyshev.
    [Show full text]