Joint Dynamics of Bond and Stock Returns
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2021 Mid-Year Outlook July 2021 Economic Recovery, Updated Vaccine, and Portfolio Considerations
2021 Mid-Year Outlook July 2021 Economic recovery, updated vaccine, and portfolio considerations. Key Observations • Financial market returns year-to-date coincide closely with the premise of an expanding global economic recovery. Economic momentum and a robust earnings backdrop have fostered uniformly positive global equity returns while this same strength has been the impetus for elevated interest rates, hampering fixed income returns. • Our baseline expectation anticipates that the continuation of the economic revival is well underway but its relative strength may be shifting overseas, particularly to the Eurozone, where amplifying vaccination efforts and the prospects for additional stimulus reign. • Our case for thoughtful risk-taking remains intact. While the historically sharp and compressed pace of the recovery has spawned exceptionally strong returns across many segments of the capital markets and elevated valuations, the economic expansion should continue apace, fueled by still highly accommodative stimulus, reopening impetus and broader vaccination. Financial Market Conditions Economic Growth Forecasts for global economic growth in 2021 and 2022 remain robust with the World Bank projecting a 5.6 percent growth rate for 2021 and a 4.3 percent rate in 2022. If achieved, this recovery pace would be the most rapid recovery from crisis in some 80 years and provides a full reckoning of the extraordinary levels of stimulus applied to the recovery and of the herculean efforts to develop and distribute vaccines. GDP Growth Rates Source: FactSet Advisory services offered through Veracity Capital, LLC, a registered investment advisor. 1 While the case for further global economic growth remains compelling, we are mindful that near-term base effect comparisons and a bifurcated pattern of growth may be masking some complexities of the recovery. -

Relative Strength Index for Developing Effective Trading Strategies in Constructing Optimal Portfolio
International Journal of Applied Engineering Research ISSN 0973-4562 Volume 12, Number 19 (2017) pp. 8926-8936 © Research India Publications. http://www.ripublication.com Relative Strength Index for Developing Effective Trading Strategies in Constructing Optimal Portfolio Dr. Bhargavi. R Associate Professor, School of Computer Science and Software Engineering, VIT University, Chennai, Vandaloor Kelambakkam Road, Chennai, Tamilnadu, India. Orcid Id: 0000-0001-8319-6851 Dr. Srinivas Gumparthi Professor, SSN School of Management, Old Mahabalipuram Road, Kalavakkam, Chennai, Tamilnadu, India. Orcid Id: 0000-0003-0428-2765 Anith.R Student, SSN School of Management, Old Mahabalipuram Road, Kalavakkam, Chennai, Tamilnadu, India. Abstract Keywords: RSI, Trading, Strategies innovation policy, innovative capacity, innovation strategy, competitive Today’s investors’ dilemma is choosing the right stock for advantage, road transport enterprise, benchmarking. investment at right time. There are many technical analysis tools which help choose investors pick the right stock, of which RSI is one of the tools in understand whether stocks are INTRODUCTION overpriced or under priced. Despite its popularity and powerfulness, RSI has been very rarely used by Indian Relative Strength Index investors. One of the important reasons for it is lack of Investment in stock market is common scenario for making knowledge regarding how to use it. So, it is essential to show, capital gains. One of the major concerns of today’s investors how RSI can be used effectively to select shares and hence is regarding choosing the right securities for investment, construct portfolio. Also, it is essential to check the because selection of inappropriate securities may lead to effectiveness and validity of RSI in the context of Indian stock losses being suffered by the investor. -

Term Premium Puzzle: ∗ an Alternative Explanation ∗ Udc 336.71 336.76 336.67
FACTA UNIVERSITATIS Series: Economics and Organization Vol. 1, No 9, 2001, pp. 73 - 84 TERM PREMIUM PUZZLE: ∗ AN ALTERNATIVE EXPLANATION ∗ UDC 336.71 336.76 336.67 Srdjan Marinković Faculty of Economics, University of Niš, 18000 Niš, Yugoslavia Abstract. For a long time the significant yield differential between extremely short- term and other short-term default-free government securities, i.e. short-end of yield curve slope has remained unexplained in the economic science. This phenomenon is known as 'term premium puzzle'. Prevailing theory based on consumption failed to explain many other empirically prooved market developments. We offer an explanation to solve the puzzle. The significance of those findings is far reaching than reviling the puzzle. Basic concept is already successfully used to explain many institutional developments, financial intermediary, for example, and can be also used to restate asset-pricing models and the theory of financial crises and disturbances. Key words: yield curve, term premium, liquidity premium, uncertainty, the theory of bank. SHORTCOMINGS OF THE PREVAILING THEORY Consumption based theory of asset pricing seems to say little about various stylised facts concerning the yield curve, such as its predominantly upward slope. This feature of yield curve is especially obvious in its short-end. It implies that short and long-term de- fault risk-free debts are not perfectly substitutable. Time-persistent spread between treas- ury bills maturing for tree and six months, known as 'term premium puzzle', can be ex- plained by means of merely neglected influence of time-horizon on predictability and, as a consequence, on market information efficiency as well. -

W E B R E V Ie W
TRADERS´ TOOLS 37 Professional Screening, Advanced Charting, and Precise Sector Analysis www.chartmill.com The website www.chartmill.com is a technical analysis (TA) website created by traders for traders. Its main features are charting applications, a stock screener and a sector analysis tool. Chartmill supports most of the classical technical analysis indicators along with some state-of-the-art indicators and concepts like Pocket Pivots, Effective Volume, Relative Strength and Anchored Volume Weighted Average Prices (VWAPs, MIDAS curves). First, we will discuss some of these concepts. After that, we will have a look at the screener and charting applications. Relative Strength different manner. This form of Strong Stocks flatten out again. “Strong stocks” Relative Strength is available in Relative Strength was used in The screener supports the filters the nicest steady trends WEBREVIEW different forms at chartmill.com. “Point and Figure Charting” by concept of “strong stocks”, in the market and does a terrific Two Relative Strength related Thomas Dorsey. which are stocks with a high job in mimicking IBD (Investor‘s indicators are available in the Relative Strength. But there is Business Daily) stock lists. charts and screener: Besides these two indicators, more. Not all stocks with a high there is also the Relative Strength Relative Strength ranking are also Effective Volume • Mansfield Relative Strength: Ranking Number. Here, each strong stocks. Relative Strength Effective Volume is an indicator This compares the stock gets assigned a number looks at the performance over that was introduced in the book performance of the stock to between zero and 100, indicating the past year. -

Point and Figure Relative Strength Signals
February 2016 Point and Figure Relative Strength Signals JOHN LEWIS / CMT, Dorsey, Wright & Associates Relative Strength, also known as momentum, has been proven to be one of the premier investment factors in use today. Numerous studies by both academics and investment ABOUT US professionals have demonstrated that winning securities continue to outperform. This phenomenon has been found Dorsey, Wright & Associates, a Nasdaq Company, is a in equity markets all over the globe as well as commodity registered investment advisory firm based in Richmond, markets and in asset allocation strategies. Momentum works Virginia. Since 1987, Dorsey Wright has been a leading well within and across markets. advisor to financial professionals on Wall Street and investment managers worldwide. Relative Strength strategies focus on purchasing securities that have already demonstrated the ability to outperform Dorsey Wright offers comprehensive investment research a broad market benchmark or the other securities in the and analysis through their Global Technical Research Platform investment universe. As a result, a momentum strategy and provides research, modeling and indexes that apply requires investors to purchase securities that have already Dorsey Wright’s expertise in Relative Strength to various appreciated quite a bit in price. financial products including exchange-traded funds, mutual funds, UITs, structured products, and separately managed There are many different ways to calculate and quantify accounts. Dorsey Wright’s expertise is technical analysis. The momentum. This is similar to a value strategy. There are Company uses Point and Figure Charting, Relative Strength many different metrics that can be used to determine a Analysis, and numerous other tools to analyze market data security’s value. -

Price Momentum Model Creat- Points at Institutionally Relevant John Brush Ed by Columbine Capital Services, Holding Periods
C OLUMBINE N EWSLETTER A PORTFOLIO M ANAGER’ S R ESOURCE SPECIAL EDITION—AUGUST 2001 From etary price momentum model creat- points at institutionally relevant John Brush ed by Columbine Capital Services, holding periods. Columbine Alpha's Inc. The Columbine Alpha price dominance comes from its exploita- Price Momentum momentum model has been in wide tion of some of the many complex- a Twenty Year use by institutions for more than ities of price momentum. Recent Research Effort twenty years, both as an overlay non-linear improvements to with fundamental measures, and as Columbine Alpha incorporating Summary and Overview a standalone idea-generating screen. adjustments for extreme absolute The evidence presented here sug- price changes and considerations of Even the most casual market watch - gests that price momentum is not a trading volume appear likely to add ers have observed anecdotal evi- generic ingredient. another 100 basis points to the dence of trend following in stock model's 1st decile active return. prices. Borrowing from the world of The Columbine Alpha approach physics, early analysts characterized is almost twice as powerful as the You will see in this paper that this behavior as stock price momen- best simple alternative and war- constructing a price momentum tum. Over the years, researchers and rants attention by any investment model involves compromises or practitioners have developed manager who cares about active tradeoffs driven by the fact that increasingly more sophisticated return. different past measurement peri- mathematical descriptions (models) ods produce different future of equity price momentum effects. Even simple price momentum return patterns. -

The Total Risk Premium Puzzle
FEDERAL RESERVE BANK OF SAN FRANCISCO WORKING PAPER SERIES The Total Risk Premium Puzzle Òscar Jordà Federal Reserve Bank of San Francisco University of California, Davis Moritz Schularick University of Bonn CEPR Alan M. Taylor University of California, Davis NBER CEPR March 2019 Working Paper 2019-10 https://www.frbsf.org/economic-research/publications/working-papers/2019/10/ Suggested citation: Jordà, Òscar, Moritz Schularick, Alan M. Taylor. 2019. “The Total Risk Premium Puzzle,” Federal Reserve Bank of San Francisco Working Paper 2019-10. https://doi.org/10.24148/wp2019-10 The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Federal Reserve Bank of San Francisco or the Board of Governors of the Federal Reserve System. The Total Risk Premium Puzzle ? Oscar` Jorda` † Moritz Schularick ‡ Alan M. Taylor § March 2019 Abstract The risk premium puzzle is worse than you think. Using a new database for the U.S. and 15 other advanced economies from 1870 to the present that includes housing as well as equity returns (to capture the full risky capital portfolio of the representative agent), standard calculations using returns to total wealth and consumption show that: housing returns in the long run are comparable to those of equities, and yet housing returns have lower volatility and lower covariance with consumption growth than equities. The same applies to a weighted total-wealth portfolio, and over a range of horizons. As a result, the implied risk aversion parameters for housing wealth and total wealth are even larger than those for equities, often by a factor of 2 or more. -

How Speculation Can Explain the Equity Premium
How speculation can explain the equity premium Glenn Shafer and Vladimir Vovk The Game-Theoretic Probability and Finance Project Working Paper #47 First posted October 16, 2016. Last revised January 1, 2018. Project web site: http://www.probabilityandfinance.com Abstract When measured over decades in countries that have been relatively stable, re- turns from stocks have been substantially better than returns from bonds. This is often attributed to investors' risk aversion: stocks are thought to be riskier than bonds, and so investors will pay less for an expected return from stocks than for the same expected return from bonds. The game-theoretic probability-free theory of finance advanced in our 2001 book Probability and Finance: It's Only a Game suggests an alternative ex- planation, which attributes the equity premium to speculation. This game- theoretic explanation does better than the explanation from risk aversion in accounting for the magnitude of the premium. Contents 1 Introduction 1 2 What causes volatility? 1 3 What is an efficient market? 2 3.1 The efficient index hypothesis (EIH) . 3 3.2 Mathematical implications of the EIH . 4 4 The equity premium 5 4.1 Why the premium is a puzzle . 5 4.2 The premium implied by the EIH . 6 4.3 The trading strategy that implies the premium . 6 4.4 Implications of the premium . 7 5 The game-theoretic CAPM 8 6 Need for empirical work 9 6.1 Attaining efficiency . 9 6.2 Measuring the equity premium . 9 6.3 Testing the game-theoretic CAPM . 10 7 Acknowledgements 11 8 Relevant GTP papers 11 Other references 12 1 Introduction The game-theoretic probability-free theory of finance advanced in our 2001 book Probability and Finance: It's Only a Game and in subsequent working papers (see Section 8) suggests that the equity premium can be explained by specula- tion. -
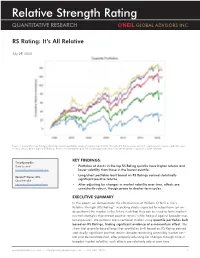
Relative Strength Rating QUANTITATIVE RESEARCH
Relative Strength Rating QUANTITATIVE RESEARCH RS Rating: It’s All Relative July 29, 2020 Figure 1: Cumulative monthly log returns for quantile portfolios constructed based on Relative Strength (RS) Rating across our U.S. equity market universe, with Q5 repre- senting stocks with the highest RS Ratings. Results are liquidity-weighted and normalized with respect to intertemporal changes in market volatility. KEY FINDINGS: Timothy Marble Data Scientist • Portfolios of stocks in the top RS Rating quintile have higher returns and [email protected] lower volatility than those in the lowest quintile. • Long/short portfolios built based on RS Ratings earned statistically Ronald P. Ognar, CFA Quant Analyst significant positive returns. [email protected] • After adjusting for changes in market volatility over time, effects are consistently robust, though prone to shorter-term cycles. EXECUTIVE SUMMARY In this paper, we demonstrate the effectiveness of William O’Neil + Co.’s Relative Strength (RS) Rating™ in picking stocks expected to outperform (or un- derperform) the market in the future such that they can be used to form market- neutral strategies that extract positive returns while hedged against broader mar- ket exposures. We perform cross-sectional studies using quantile portfolios built based on RS Ratings, finding significant evidence of a momentum effect. We show that quantile-based long/short portfolios built based on RS Rating earned statistically significant positive returns despite remaining ostensibly market neu- tral and demonstrate that, after properly adjusting for changes through time in broader market volatility, such effects are relatively robust over time. oneilglobaladvisors.com • [email protected] • 310.448.3800 1 Relative Strength Rating INTRODUCTION RELATIVE STRENGTH RATING™ (RS) William O’Neil + Co.’s proprietary Relative Strength Rating measures a stock’s relative price performance over the last 12 months against that of all stocks in our U.S. -

The Grand Finale: Choosing an Investment Philosophy
The Grand Finale: Choosing an Investment Philosophy! Aswath Damodaran Aswath Damodaran! 1! A Self Assessment! " To chose an investment philosophy, you first need to understand your own personal characteristics and financial characteristics, as well as as your beliefs about how markets work (or fail). " An investment philosophy that does not match your needs or your views about markets will ultimately fail. Aswath Damodaran! 2! Personal Characteristics! " Patience: Some investment strategies require a great deal of patience, a virtue that many of us lack. If impatient by nature, you should consider adopting an investment philosophy that provides payoffs in the short term. " Risk Aversion: If you are risk averse, adopting a strategy that entails a great deal of risk – trading on earnings announcements, for instance – will not be a strategy that works for you in the long term. " Individual or Group Thinker: Some investment strategies require you to go along with the crowd and some against it. Which one will be better suited for you may well depend upon whether you are more comfortable going along with the conventional wisdom or whether you are a loner. " Time you are willing to spend on investing: Some investment strategies are much more time and resource intensive than others. Generally, short-term strategies that are based upon pricing patterns or on trading on information are more time and information intensive than long-term buy and hold strategies. " Age: As you age, you may find that your willingness to take risk, especially with your retirement savings, decreases.. It is true, though, that even as a successful investor, you will have learnt lessons from prior investment experiences that will both constrain and guide your choice of philosophy. -

Relative Strength Index (RSI)
Understanding Technical Analysis : Relative Strength Index (RSI) Understanding Relative Strength Index Hi 74.57 Relative Strength Index (RSI) is a technical indicator that is categorised under Potential supply momentum indicator. Basically, all momentum indicators measures thedisruption rate dueof riseto and fall of the financial instrument's price. Usually, momentum attacksindicators on two oilare dependent indicators as they are best used with other indicators sincetankers they near do Iran not tell the traders or analysts the potential direction of the financial instrument. Among Brent the popular type of momentum indicators are Stochastic Indicator, Commodity Channel Index and Relative Strength Index. In this factsheet, we will explore the Relative Strength Index or better known as RSI. What is RSI? WTI Developed by J. Welles Wilder Jr. in his seminal 1978 book, "New Concepts in Technical Trading WTI Systems." Measures the speed and change of price movement of the financial instruments. As RSI is a type of oscillator, thisLo 2,237.40indicator is represented as a set of line that has(24 values Mar 2020) from 0 to 100. Generally, a reading below 30 indicatesLo 18,591.93 an oversold condition, while a value above (2470 Mar signals 2020) an overbought condition. Leading vs Lagging Indicator RSI is a leading type of indicator. A leading type of indicator is an indicator that can provide the traders or analyst with future price movement. Another example of leading indicator is Stochastic Indicator. In contrast, a lagging indicator is an indicator that follows the price movement of the financial instruments. Despite their lagging nature in providing trading signals, traders or analysts prefer to use lagging indicators as they are more reliable. -

NBER WORKING PAPER SERIES FLIGHT to QUALITY, FLIGHT to LIQUIDITY, and the PRICING of RISK Dimitri Vayanos Working Paper 10327 Ht
NBER WORKING PAPER SERIES FLIGHT TO QUALITY, FLIGHT TO LIQUIDITY, AND THE PRICING OF RISK Dimitri Vayanos Working Paper 10327 http://www.nber.org/papers/w10327 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts Avenue Cambridge, MA 02138 February 2004 I thank Viral Acharya, John Cox, Xavier Gabaix, Denis Gromb, Tim Johnson, Leonid Kogan, Pete Kyle, Jonathan Lewellen, Hong Liu, Stew Myers, Jun Pan, Anna Pavlova, Steve Ross, Jiang Wang, Wei Xiong, Jeff Zwiebel, seminar participants at Amsterdam, Athens, Caltech, LSE, LBS, Michigan, MIT, NYU, Princeton, Stockholm, Toulouse, UBC, UCLA, UT Austin, Washington University, and participants at the Econometric Society 2003 Summer Meetings, for helpful comments. I am especially grateful to Jeremy Stein for discussions that helped define this project, and for insightful comments in later stages. Jiro Kondo provided excellent research assistance. Financial support for this research came from the MIT/Merrill Lynch partnership. The views expressed herein are those of the authors and not necessarily those of the National Bureau of Economic Research. ©2004 by Dimitri Vayanos. All rights reserved. Short sections of text, not to exceed two paragraphs, may be quoted without explicit permission provided that full credit, including © notice, is given to the source. Flight to Quality, Flight to Liquidity, and the Pricing of Risk Dimitri Vayanos NBER Working Paper No. 10327 February 2004 JEL No. G1, G2 ABSTRACT We propose a dynamic equilibrium model of a multi-asset market with stochastic volatility and transaction costs. Our key assumption is that investors are fund managers, subject to withdrawals when fund performance falls below a threshold. This generates a preference for liquidity that is time- varying and increasing with volatility.