DOCSLIB.ORG

Morphodynamic Response of Spencer Creek to Large Precipitation Events and Channel Modifications: a Case Study

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Morphodynamic Response of Spencer Creek to Large Precipitation Events and Channel Modifications: a Case Study Western University Scholarship@Western Electronic Thesis and Dissertation Repository 7-27-2017 12:00 AM Morphodynamic Response of Spencer Creek to Large Precipitation Events and Channel Modifications: A Case Study Emily Mae Martin The University of Western Ontario Supervisor Dr. Andrew Binns The University of Western Ontario Joint Supervisor Dr. Timothy Newson The University of Western Ontario Graduate Program in Civil and Environmental Engineering A thesis submitted in partial fulfillment of the equirr ements for the degree in Master of Engineering Science © Emily Mae Martin 2017 Follow this and additional works at: https://ir.lib.uwo.ca/etd Part of the Environmental Engineering Commons Recommended Citation Martin, Emily Mae, "Morphodynamic Response of Spencer Creek to Large Precipitation Events and Channel Modifications: A Case Study" (2017). Electronic Thesis and Dissertation Repository. 4870. https://ir.lib.uwo.ca/etd/4870 This Dissertation/Thesis is brought to you for free and open access by Scholarship@Western. It has been accepted for inclusion in Electronic Thesis and Dissertation Repository by an authorized administrator of Scholarship@Western. For more information, please contact [email protected]. Abstract Severe weather events are occurring more frequently with extreme repercussions as our climate changes. Rainfall events of large magnitudes can lead to instability of river banks, riverbed erosion, and alterations in stream planform alignment. It is important to understand the hydraulic and geomorphic response of rivers and streams to storm events to predict long term morphological change, protect hydraulic structures, and manage aquatic ecosystems. The goal of this thesis is to examine the influence of precipitation events of varying magnitude on the morphodynamic processes of an urban creek. Four events are simulated: a constant averaged flow of 1.249 m3/s representative of the average flow in the creek over a 5-year period, a 5- year return period event, a 10-year return period event, and a 100-year return period event. Channel modifications are made to four cross sections at the downstream end of Spencer Creek in order to investigate the effect of planform alignment and geometry on increased flood resiliency and channel stability. The first modification widened the channel at these sections, while the second modification lengthened the channel at these sections to be representative of increased meandering (and corresponding decrease in stream bed slope) of the creek. In general, the sediment concentration changed with each event, with the largest sediment concentration in the channel occurring for the 100-year return period event. The first modification to the channel demonstrated the largest reduction in velocity, sediment concentration, and shear stress at all cross sections for all events. The second modification demonstrated little to no change in velocity and shear stress for all events. The results from this thesis provide a framework for analyzing the morphodynamic response of urban streams to storm events of varying return periods and durations and will assist river engineers and hydrologists in managing and restoring urban creeks to mitigate flooding while balancing erosion and ecological processes. Keywords Mathematical modeling, sediment transport, channel modification, rivers and streams, hydraulic modeling i Acknowledgments I would like to express my extreme gratitude towards my supervisors Dr. Andrew D. Binns and Dr. Tim Newson for providing me with this opportunity. Thank you for your guidance, support, encouragement, advice, and financial support throughout my degree. Thank you to my research group, the Binns Group, for their support and assistance throughout my degree. I would like specifically to thank Etta Gunsolus for motivating and inspiring me when times were tough. Her ability to find the silver lining in any situation helped me when life didn’t go as planned. This thesis would not have been possible without the love and support of my family and friends. Thank you to my parents, Lori and Terry, for always pushing me to do my best and for helping me look on the bright side of every situation. Thank you to my future mother- and father-in-law, Becky and Baba, for their support and care packages. I would also like to thank my girlfriends: Robyn, Julia, Amy, Michelle, and Katie for inspiring me every day. I would especially like to thank my partner, Sam, for standing by me throughout my academic studies. His encouragement to apply to the program, his constant love and support throughout my degree, and his strong work ethic pushed me to complete this thesis. I am excited to see what the future holds for us. Finally, a special thank you to my late grandmother, Phyllis Chapman, for her support and her contagious positivity throughout my academic studies until her final days. She was my biggest cheerleader, and I would not have reached this point without her. ii Table of Contents Abstract ................................................................................................................................ i Acknowledgments............................................................................................................... ii Table of Contents ............................................................................................................... iii List of Tables ..................................................................................................................... vi List of Figures .................................................................................................................. viii List of Appendices ........................................................................................................... xiii List of Symbols ................................................................................................................ xiv Chapter 1 ............................................................................................................................. 1 1 Introduction .................................................................................................................... 1 1.1 General .................................................................................................................... 1 1.2 Goal and Objectives ................................................................................................ 3 1.3 Structure of Thesis .................................................................................................. 4 Chapter 2 ............................................................................................................................. 6 2 Fundamentals of the Present Work ................................................................................ 6 2.1 Fundamental Equations ........................................................................................... 6 2.1.1 Fundamental Equations of Flow ................................................................. 7 2.1.2 Fundamental Equations of Sediment Motion ............................................. 9 2.1.3 Fundamental Equations of Shear Stress .................................................... 12 2.1.4 Fundamental Equations of Bank Erosion ................................................. 13 2.2 Mathematical Modeling ........................................................................................ 17 2.2.1 HEC-RAS ................................................................................................. 17 Chapter 3 ........................................................................................................................... 20 3 Literature Review ......................................................................................................... 20 3.1 Stream Restoration and Channel Design .............................................................. 20 iii 3.2 Mathematical Modeling ........................................................................................ 23 3.3 Summary ............................................................................................................... 26 Chapter 4 ........................................................................................................................... 28 4 Study Area and Methodology ...................................................................................... 28 4.1 Flooding in Southwestern Ontario ........................................................................ 28 4.2 Study Area ............................................................................................................ 30 4.2.1 Previous Alterations to Spencer Creek ..................................................... 34 4.3 Methodology ......................................................................................................... 36 4.3.1 Hydrographs .............................................................................................. 37 4.3.2 Channel Modifications .............................................................................. 39 4.3.3 Simulations ............................................................................................... 40 4.3.4 Model Set-up ............................................................................................. 42 Chapter 5 ........................................................................................................................... 44 5 Results .........................................................................................................................
Load more

Recommended publications
  • Feature Sheet the Opus Team
    THEOPUSTEAM FEATURE SHEET THE OPUS TEAM Andrew Bridgman Derek Keyes 4 Country Club Drive Celina Nowak Hamilton, Ontario www.THEOPUSTEAM.com Streetcity Realty Inc., Brokerage (905) 634-9476 THEOPUSTEAM OVERVIEW 4 Country Club Drive Offered at $334,000 • 3 bedroom • 2 bathroom This a great 3 bedroom semi-detached house in the wonderful mature King’s Forest neighbourhood. The property is close to all the amenities on Centennial (Highway 20) and King Street East. It’s also very close to Eastgate Square Shopping Centre. Easy access to Red Hill Valley Parkway. Same owner for many years. Great renovation potential to turn this house into a home. It’s all right here. THEOPUSTEAM Andrew Bridgman, Derek Keyes & Celina Nowak Streetcity Realty Inc., Brokerage 247 Centennial Parkway N., #15, Hamilton, Ontario, L8N 1E8, Canada 905-664-5000 | [email protected] | www.TheOPUSteam.com THEOPUSTEAM THE DETAILS Lot Size: Area: 3767.36 sq.ft Perimeter: 301.84 ft Measurements: 31.4ft. x 120.25ft. x 31.4ft. x 120.25ft. Frontage: 31.33 ft. Depth: 120.0 ft. Notables: • Open Kitchen Potential • Spacious Bedrooms • Basement Family Room • Great Back Yard • Ample Parking • Great Neighbourhood THEOPUSTEAM Andrew Bridgman, Derek Keyes & Celina Nowak Streetcity Realty Inc., Brokerage 247 Centennial Parkway N., #15, Hamilton, Ontario, L8N 1E8, Canada 905-664-5000 | [email protected] | www.TheOPUSteam.com THEOPUSTEAM PHOTOS THEOPUSTEAM Andrew Bridgman, Derek Keyes & Celina Nowak Streetcity Realty Inc., Brokerage 247 Centennial Parkway N., #15, Hamilton, Ontario, L8N 1E8, Canada 905-664-5000 | [email protected] | www.TheOPUSteam.com THEOPUSTEAM About Streetcity Streetcity Inc. Brokerage is a new and exciting brokerage and we are pleased to be a part of the family.
    [Show full text]
  • Bringing Back The
    Ba BBrriinnggiinngg BBaacckk tthhee Bayy Number 60 Spring 2008 BARC Newsletter BARC’s First Fundraiser a Great Success! BY CINDY SMITH, COMMUNICATIONS MANAGER n a chilly January evening, the Bay OArea Restoration Council hosted its ve r y f i r s t f u n d r a i s e r. W h a t a g r e a t eve n i n g we had! Patrons at our Wine Tasting & Silent Auction filled the Royal Hamilton Yacht Club to support the restoration and protection of our harbour. Guests enjoyed hot and cold appetizers as well as free wine and beer sampling while listening to a musical duo who entertained us throughout the evening. Sunni Genesco, Morning Show Host on K-Lite FM, did a fabulous job as Master of Ceremonies, keeping us apprised of table closings and random closings of some of the hot items. Photo Credits: Cindy Smith Sophia Aggelonitis; jewellery; Ti-Cat Area and AGH; a co-hosting spot on the Friendly competition erupted early on memorabilia; guided nature hikes; CHML Morning Show; one-of-a-kind as bidding began on the auction items. memberships to RBG, the Warplane ceramics; original artwork; concert and There was a vast array of items including Heritage Museum, the Conservation theatre tickets; as well as a helicopter golfing; restaurant gift certificates; spa ride around the bay. packages; books; boat cruises; lunch with Mayor Eisenberger; lunch with The event’s success was thanks to our sponsors, ticket buyers, auction TABLE OF CONTENTS participants, Steam Whistle Brewing, participating wineries, the yacht club Bay Watch .
    [Show full text]
  • PUBLIC WORKS COMMITTEE MINUTES 16-015 9:30 A.M
    PUBLIC WORKS COMMITTEE MINUTES 16-015 9:30 a.m. Monday, September 19, 2016 Council Chambers Hamilton City Hall 71 Main Street West _____________________________________________________________________ Present: Councillor T. Whitehead (Chair) Councillor A. VanderBeek (Vice Chair) Councillors S. Merulla, C. Collins, T. Jackson, D. Conley, L. Ferguson and R. Pasuta Also Present: Councillors J. Farr and B. Johnson ____________________________________________________________________ THE FOLLOWING ITEMS WERE REPORTED TO COUNCIL FOR CONSIDERATION: 1. 2016 Special Events Requiring Temporary Road Closures (PW16083) (Ward 2) (Item 5.1) (Conley/Jackson) That each of the following applications: (a) Core Entertainment for the temporary closure of Bay Street between King Street and York Boulevard on Friday October 7, 2016 for a Toronto Maple Leafs Pre-Season Game Street Event; (b) Vanier Cup Host Committee for the temporary closure of King William Street between James Street and Hughson Street on Friday November 11, 2016 for a Vanier Cup Street Event. Be approved, subject to the following conditions: (i) That the City may revoke the temporary road closure at any time to gain access for emergency services; (ii) That no property owner or resident within the barricaded area be denied access to their property upon request; Public Works Committee September 19, 2016 Minutes 16-015 Page 2 of 13 (iii) That the applicant ensure that clean-up operations be carried out immediately before the re-opening of the roads, to the satisfaction of the General Manager
    [Show full text]
  • CITY COUNCIL MINUTES 19-012 5:00 P.M
    4.1 CITY COUNCIL MINUTES 19-012 5:00 p.m. June 26, 2019 Council Chamber Hamilton City Hall 71 Main Street West Present: Mayor F. Eisenberger Councillors B. Johnson (Deputy Mayor), B. Clark, C. Collins, J.P. Danko, J. Farr, L. Ferguson, T. Jackson, S. Merulla, N. Nann, J. Partridge, E. Pauls, M. Pearson, A. VanderBeek, T. Whitehead and M. Wilson Mayor Eisenberger called the meeting to order and recognized that Council is meeting on the traditional territories of the Mississauga and Haudenosaunee nations, and within the lands protected by the “Dish with One Spoon” Wampum Agreement. The Mayor called upon Pastor Michelle Daniel of Crossfire Assembly, to provide the invocation. APPROVAL OF THE AGENDA The Clerk advised of the following changes to the agenda: 1. COMMUNICATIONS (Item 5) 5.12 Correspondence respecting recent incidents that have occurred on City property and the Hamilton Pride 2019: (a) Darren Stewart-Jones (b) Sally Cooper (c) Emma Cole (d) Anna Chatterton (e) Talia Ritondo (f) First Unitarian Church of Hamilton (g) Frances Murray (h) Noelle Allen Recommendation: Be received and referred to the consideration of Item (i)(i) of General Issues Committee Report 19-012. Council Minutes 19-012 June 26, 2019 Page 2 of 54 5.13 Correspondence respecting the Update on Safety Measures on Aberdeen Avenue from Queen Street to Longwood Road: (a) Joshua Weresch (b) Ron McKerlie, President, Mohawk College (c) Alex Baker (d) Marc Ayotte, Head of College, Hillfield Strathallan College (e) Duncan Macintosh, Owner, Soccer World (f) Vincent Chan, Assistant General Manager, Columbia International College (g) Ramnarine Family (h) Colin Lyons, Vice President, Mohawk Medbuy Corporation (i) Barb Howe Recommendation: Be received and referred to the consideration of Item 7 of Public Works Committee Report 19-009.
    [Show full text]
  • Driving Directions to the JCC
    Driving directions to the JCC There are two parking lots near the JCC. One is on Concession Street and the other is on Poplar Avenue. When you arrive at the JCC, please come to the Information Desk in the lobby. You will be directed to the clinic for your appointment. From St. Catharines Take the QEW to the Centennial Parkway/Red Hill Valley Parkway exit. Then follow the sign for the Red Hill Valley Parkway exit. The parkway becomes the Lincoln Alexander Parkway. Exit onto Upper Gage. Turn right on Upper Gage and follow until you reach Concession Street. Turn left onto Concession Street. The JCC is on the right side of the street, several blocks up. From Cambridge Take Hwy #52 to Hwy #403. Take the Lincoln Alexander Parkway (LINC) exit and follow the LINC to Upper Wentworth Street. Exit the LINC and travel north on Upper Wentworth. At Concession Street turn right. Continue for 3 blocks. The JCC is on the left side of the street. From Brantford Take Hwy #403. Take the Lincoln Alexander Parkway (LINC) exit east and follow the LINC to Upper Wentworth Street. Exit the LINC and travel north on Upper Wentworth. At Concession Street turn right. Continue for 3 blocks. The JCC is on the left side of the street. From Toronto Take QEW to Hwy 403 -- then as below From Guelph Take Hwy 6 to Hwy 403 west -- then as below Exit from Hwy #403. Take the Lincoln Alexander Parkway (LINC) exit east and follow the LINC to Upper Wentworth Street. Exit the LINC and travel north on Upper Wentworth.
    [Show full text]
  • Directions to Fennell Campus
    Fennell Campus, Mohawk College 135 Fennell Avenue West (at the corner of West 5th St) Hamilton, Ontario, Canada L9C 1E9 Phone: (905) 575-1212 Fennell Avenue General Parking StudentPreferred Residence Parking Visitor’s Parking/Pay & Display Carpooling Fitness Centre McKeil School of Business Fennell Avenue P10 Future Student Residence H-WingH Fitness Centre$ $ Student Alumni Centre IT Centre A House P9 P15 P14 Residence Future 5th Street West $ Parking P8 J P8 Only General Parking G H-WingH Preferred Student E Parking Centre $ A n P14 $ P7 DBARC$ C 5th Street West General ParkingP13 MSAG J General Parking Plaza E P6 General Parking $ $ n Outdoor Courts B P1 P11 P12 F C General Parking Preferred Parking P5 General Parking P4 M Data P1 Visitor Centre Parking Preferred Parking $ F Main Entrance B P5 P3 Barrier-Free P10 $ P2 General Parking M Vehicle Charging Station Today’s Family Drop-off GovernorsP4 Blvd Visitor’s P2 P3 Parking/ $ Preferred Pay &Display I Parking Designated Smoking Area Emergency Phone Preferred Parking P6 EntranceEmergency Phone Accessible Parking General Parking Designated Smoking Area Emergency Phone I Information Kiosk Today’s Family Drop-off Governors Blvd 04/2016 Entrance Main Pick-up/Drop-offDisabled Area Parking $ Parking$ Pay &Pay Display Station Machine Carpooling 08/2010 Directions From points north and east From points southeast (i.e. Niagara/St. Catharines): (Toronto/Oakville/Burlington/Guelph): • QEW West to Hamilton • Hwy #403 West to Hamilton • Exit at the Red Hill Valley Parkway • Exit at Aberdeen Avenue (can only go east) • Come up the "Mountain" and continue onto • Turn right on Queen Street / Beckett Ave (Mountain Access) the Lincoln Alexander Parkway ("The Linc") west • Turn left on Fennell Avenue at the first stop light • Exit at Upper James Street and turn right (north) at the top of the "Mountain" • Turn left (west) on Mohawk Road (second stop light) • Mohawk College, Fennell Campus is on your right • Turn right (north) on West 5th St.
    [Show full text]
  • Culture Report Final April 23
    Appendix A to Report CS10057 Page 1 of 175 our community culture project phase 1 report - baseline cultural mapping realizing Hamilton’s potential as a creative city may 1, 2010 Appendix A to Report CS10057 Page 1 of 175 our community culture project phase 1 report - baseline cultural mapping realizing Hamilton’s potential as a creative city may 1, 2010 The photograph on the cover of this report is of the underside of the Birks Clock. The Birks Clock is part of the City of Hamilton’s Art in Public Places Collection. First located on the corner of what became the Birks Building at James South and King East, the clock was moved to the entrance of Jackson Square. The fully restored clock will hang in the Hamilton Farmers’ Market on York Blvd. Report produced by AuthentiCity for the Culture Division, Community Services Department, City of Hamilton. table of contents Photograph by Jeff Tessier Dining Room at Whitehern Historic House & Garden - Hamilton Civic Museums table of contents 5 table of contents Letter of Introduction 7 Executive Summary 10 1 Cultural Planning Definitions 20 2 Cultural Mapping Findings 26 What is Cultural Mapping? 28 OCC Phase 1 - Mapping Goals and Process 30 OCC Phase 1 - Mapping Results 32 An Ongoing Cultural Mapping System for Hamilton 36 Next Steps in Cultural Mapping 38 3 Understanding the Planning Context 40 The Creative Economy 42 Culture and Planning for Sustainability 46 Culture and Place Competitiveness 46 4 Integrating Culture in City Planning 48 Statistical Snapshot of Hamilton 50 Strategic Themes for Phase
    [Show full text]
  • Eli S. Lederman | Lenczner Slaght
    1 Eli S. Lederman ELI S. LEDERMAN is a partner at Lenczner Slaght. Eli's practice covers a broad range of complex commercial litigation matters, including securities law, class actions, commercial contracts, franchise disputes, oppression and other shareholder litigation. He regularly acts for directors and officers of private and public corporations and advises boards Education and their committees on governance and litigation matters. Dalhousie University (2001) LLB McGill University (1998) BA Eli has extensive trial experience in commercial litigation and (Distinction - History) in medical malpractice actions, and also acts as counsel in Bar Admissions Ontario (2002) commercial arbitrations. He has appeared as lead counsel at all levels of court including the Supreme Court of Canada, the Practice Areas Arbitration Court of Appeal for Ontario, the Court of Appeal for Alberta Class Actions Commercial Litigation and the Ontario Superior Court of Justice. Injunctions Professional Liability and Regulation Eli represents clients in a wide range of sectors, including those Public Law Securities Litigation in financial services, information technology, real estate, Contact franchising and manufacturing. Eli is a frequent speaker in T 416-865-3555 continuing legal education programs particularly on issues [email protected] relating to contractual disputes, securities law and trial advocacy. RECOGNITION Benchmark Canada (2013-2021) Litigation Star – Class Action, Commercial, Securities Best Lawyers in Canada (2014-2022) Administrative &
    [Show full text]
  • Draft Recreational Trails Master Plan
    Hamilton Recreational Trails Master Plan DRAFT | NOVEMBER 2015 TABLE OF CONTENTS Table of Contents .......................................................................................................................................... i-v Acknowledgments ........................................................................................................................................ vi 1.0 Study Introduction ........................................................................................................................... 1 1.1 A History of Trails in Hamilton ..................................................................................................... 1 1.2 Trail Vision, Goals, & Objectives for the City of Hamilton ............................................................ 2 1.3 The Benefi ts of Trail Development ............................................................................................. 3 1.4 The Organization of the Master Plan Report ............................................................................... 5 2.0 The Trails Network ........................................................................................................................... 6 2.1 Understanding what has Already Been Done: The Previous Trail Master Plan (2007) ................... 7 2.2 The Trail Master Plan Update Process ....................................................................................... 7 2.2.1 Trails Master Plan Opportunities .............................................................................
    [Show full text]
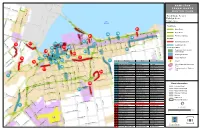
  • Map of Identified Urban Problem Areas
    T BRANT STREET E E R T HAMILTON Beeforth Road S W E d I TRUCK ROUTE Robson Road V IR a A o F L R Q A MASTER PLAN UE K EN E LIZA E r BETH S e WAY H O nn i R k E S KING ROAD E R A O S A Truck Route Review - TP D O t R Centre Road s T HIGHWAY 403 a D Problem Areas: R Hot Spots: E IV t E e e r t Lake Urban Area S Parkside Drive s PLAINS ROAD EAST a WATER Ontario d DO n W u N R OAD D Truck Routes Concession 5 East B E ea a ch st B Minor Road T po o 25 S rt ulev E D a riv rd W e D Winona Road Major Road A Lewis Road O Fifty Road R 28 North Service Road S 26 Queen Elizabeth Way N I Parkway / Highway A Fruitland Road L 23 P WoodwardAvenue Grays Road Jones Road South Service Road 30 McNeilly Road HIGHWAY 6 rd C Hot Spot a e ev ul n d o t L B e a t a P la k s o s n a e Concession 4 West e n t e O T tree Non-Designated Link R r S a 23 i on l k rt a a Millgrove Sideroad l o B Millen Road d ik D W N d l A Green Road on N e G a P 5 s a e v w r riv l .
    [Show full text]
  • MINUTES of the HAMILTON POLICE SERVICES BOARD Thursday, January 21, 2016 2:10Pm Hamilton City Hall Council Chambers the Police Services Board Met
    MINUTES OF THE HAMILTON POLICE SERVICES BOARD Thursday, January 21, 2016 2:10pm Hamilton City Hall Council Chambers The Police Services Board met There were present: Lloyd Ferguson, Chair Madeleine Levy, Vice Chair Don MacVicar Stanley Tick Terry Whitehead Absent with regrets: Fred Eisenberger Walt Juchniewicz Also Present: Acting Chief Eric Girt Deputy Chief Ken Weatherill Acting Deputy Chief Dan Kinsella Superintendent Jamie Anderson Superintendent Dave Calvert Superintendent Debbie Clark Superintendent Ryan Diodati Superintendent Paul Morrison Inspector Greg Huss Inspector Will Mason Inspector Paul McGuire Inspector Mike Worster Staff Sergeant Maggie Schoen Sergeant Jo-Ann Savoie Marco Visentini, Legal Counsel Rosemarie Auld, Manager, Human Resources Catherine Martin, Corporate Communicator Ross Memmolo, Manager, Computer Services John Randazzo, Assistant Manager, Finance Yakov Sluchenkov, Labour Relations Lois Morin, Administrator Member Ferguson called the meeting to order. Elections 2.1 Election of Chair Lois Morin the Administrator assumed the Chair and advised the Board that pursuant to Section 28 of the Police Services Act and Section 3.1 of the Police Services Board Procedural By-law, elections for the positions of Chair and Vice-Chair of the Police Services Board for 2016, would be conducted. The Administrator called for nominations for the position of Chair of the Police Services Board for 2016. It was moved by Member Levy and seconded by Member Tick that Member Ferguson be nominated for Chair of the Police Services Board for 2016. Member Ferguson indicated that he would stand for election. Police Services Board Public Minutes January 21, 2016 Page2 of6 The Administrator called for further nominations and as none were received, it was moved by Member Whitehead and seconded by Member Levy that nominations be closed.
    [Show full text]
  • 7 8 Oral Submissions on Participation and Funding 9 10
    JANUARY 10, 2020 RED HILL VALLEY PARKWAY INQUIRY Page 1 1 2 3 RED HILL VALLEY PARKWAY INQUIRY 4 5 6 ----------------- 7 8 Oral Submissions on Participation and Funding 9 10 ----------------- 11 12 13 14 HELD ON: Friday, January 10, 2020 15 16 HELD AT: Hamilton City Hall 17 Council Chambers 18 71 Main St. W. 19 Hamilton, Ontario 20 21 HELD BEFORE: 22 Mr. Justice Herman J. Wilton-Siegel - Commissioner 23 24 25 (416) 865-9339 Atchison & Denman Court Reporting (800) 259-9059 stenographers.com 155 University Avenue Toronto, ON Canada JANUARY 10, 2020 RED HILL VALLEY PARKWAY INQUIRY Page 2 1 APPEARANCES: 2 Robert A. Centa Inquiry Counsel 3 Andrew C. Lewis 4 Emily C. Lawrence 5 Hailey Bruckner 6 Shawna Leclair 7 8 Eli Lederman For the City of Hamilton 9 Delna Contractor 10 11 Heather McIvor For Her Majesty the Queen 12 in Right of Ontario 13 14 Jennifer McAleer For Dufferin Construction 15 Chris Buck Company 16 17 Jennifer Roberts For Golder Associates Ltd. 18 19 Mirle B. Chandrashekar On his own behalf 20 21 Malcolm Hodgskiss On his own behalf 22 23 H. Bruce Hillyer For Jodi Gawrylash 24 25 Dermot Nolan For Belinda Marazzato (416) 865-9339 Atchison & Denman Court Reporting (800) 259-9059 stenographers.com 155 University Avenue Toronto, ON Canada JANUARY 10, 2020 RED HILL VALLEY PARKWAY INQUIRY Page 3 1 APPEARANCES: (Cont'd) 2 3 Robert Hooper For Grosso Hooper Law and 4 Matt Moloci Scarfone Hawkins 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 (416) 865-9339 Atchison & Denman Court Reporting (800) 259-9059 stenographers.com 155 University Avenue Toronto, ON Canada JANUARY 10, 2020 RED HILL VALLEY PARKWAY INQUIRY Page 4 1 TABLE OF CONTENTS 2 3 INDEX OF PROCEEDINGS: PAGE NO.
    [Show full text]