Graphics File Formats
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Exploring the .BMP File Format
Exploring the .BMP File Format Don Lancaster Synergetics, Box 809, Thatcher, AZ 85552 copyright c2003 as GuruGram #14 http://www.tinaja.com [email protected] (928) 428-4073 The .BMP image standard is used by Windows and elsewhere to represent graphics images in any of several different display and compression options. The .BMP advantages are that each pixel is usually independently available for any alteration or modification. And that repeated use does not normally degrade the image. Because lossy compression is not used. Its main disadvantage is that file sizes are usually horrendous compared to JPEG, fractal, GIF, or other lossy compression schemes. A comparison of popular image standards can be found here. I’ve long been using the .BMP format for my eBay and my other phototography, scanning, and post processing. I firmly believe that… All photography, scanning, and all image post-processing should always be done using .BMP or a similar non-lossy format. Only after all post-processing is complete should JPEG or another compressed distribution format be chosen. Some current examples of my .BMP work now do include the IMAGIMAG.PDF post-processing tutorial, the Bitmap Typewriterthat generates fully anti-aliased small fonts, the Aerial Photo Combiner, and similar utilities and tutorials found on our Fonts & Images, PostScript, and on our Acrobat library pages. A few projects of current interest involving .BMP files include true view camera swings and tilts for a digital camera, distortion correction, dodging & burning, preventing white punchthrough on knockouts, and emphasis vignetting. Mainly applied to uncompressed RGBX 24-bit color .BMP files. -

Free Lossless Image Format
FREE LOSSLESS IMAGE FORMAT Jon Sneyers and Pieter Wuille [email protected] [email protected] Cloudinary Blockstream ICIP 2016, September 26th DON’T WE HAVE ENOUGH IMAGE FORMATS ALREADY? • JPEG, PNG, GIF, WebP, JPEG 2000, JPEG XR, JPEG-LS, JBIG(2), APNG, MNG, BPG, TIFF, BMP, TGA, PCX, PBM/PGM/PPM, PAM, … • Obligatory XKCD comic: YES, BUT… • There are many kinds of images: photographs, medical images, diagrams, plots, maps, line art, paintings, comics, logos, game graphics, textures, rendered scenes, scanned documents, screenshots, … EVERYTHING SUCKS AT SOMETHING • None of the existing formats works well on all kinds of images. • JPEG / JP2 / JXR is great for photographs, but… • PNG / GIF is great for line art, but… • WebP: basically two totally different formats • Lossy WebP: somewhat better than (moz)JPEG • Lossless WebP: somewhat better than PNG • They are both .webp, but you still have to pick the format GOAL: ONE FORMAT THAT COMPRESSES ALL IMAGES WELL EXPERIMENTAL RESULTS Corpus Lossless formats JPEG* (bit depth) FLIF FLIF* WebP BPG PNG PNG* JP2* JXR JLS 100% 90% interlaced PNGs, we used OptiPNG [21]. For BPG we used [4] 8 1.002 1.000 1.234 1.318 1.480 2.108 1.253 1.676 1.242 1.054 0.302 the options -m 9 -e jctvc; for WebP we used -m 6 -q [4] 16 1.017 1.000 / / 1.414 1.502 1.012 2.011 1.111 / / 100. For the other formats we used default lossless options. [5] 8 1.032 1.000 1.099 1.163 1.429 1.664 1.097 1.248 1.500 1.017 0.302� [6] 8 1.003 1.000 1.040 1.081 1.282 1.441 1.074 1.168 1.225 0.980 0.263 Figure 4 shows the results; see [22] for more details. -

TS 101 499 V2.2.1 (2008-07) Technical Specification
ETSI TS 101 499 V2.2.1 (2008-07) Technical Specification Digital Audio Broadcasting (DAB); MOT SlideShow; User Application Specification European Broadcasting Union Union Européenne de Radio-Télévision EBU·UER 2 ETSI TS 101 499 V2.2.1 (2008-07) Reference RTS/JTC-DAB-57 Keywords audio, broadcasting, DAB, digital, PAD ETSI 650 Route des Lucioles F-06921 Sophia Antipolis Cedex - FRANCE Tel.: +33 4 92 94 42 00 Fax: +33 4 93 65 47 16 Siret N° 348 623 562 00017 - NAF 742 C Association à but non lucratif enregistrée à la Sous-Préfecture de Grasse (06) N° 7803/88 Important notice Individual copies of the present document can be downloaded from: http://www.etsi.org The present document may be made available in more than one electronic version or in print. In any case of existing or perceived difference in contents between such versions, the reference version is the Portable Document Format (PDF). In case of dispute, the reference shall be the printing on ETSI printers of the PDF version kept on a specific network drive within ETSI Secretariat. Users of the present document should be aware that the document may be subject to revision or change of status. Information on the current status of this and other ETSI documents is available at http://portal.etsi.org/tb/status/status.asp If you find errors in the present document, please send your comment to one of the following services: http://portal.etsi.org/chaircor/ETSI_support.asp Copyright Notification No part may be reproduced except as authorized by written permission. -
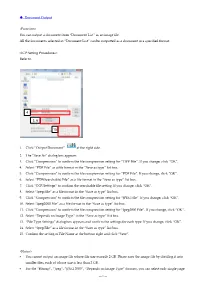
51 Document Output
◆ Document Output <Function> You can output a document from “Document List” as an image file. All the documents selected in “Document List” can be outputted as a document in a specified format. <ICP Setting Procedures> Refer to 4 3, 6 15 1. Click “Output Document” at the right side. 2. The “Save As” dialog box appears. 3. Click “Compression” to confirm the file compression setting for “TIFF File”. If you change, click “OK”. 4. Select “PDF File” as a file format in the “Save as type” list box. 5. Click “Compression” to confirm the file compression setting for “PDF File”. If you change, click “OK”. 6. Select “PDF(Searchable) File” as a file format in the “Save as type” list box. 7. Click “OCR Settings” to confirm the searchable file setting. If you change, click “OK”. 8. Select “Jpeg File” as a file format in the “Save as type” list box. 9. Click “Compression” to confirm the file compression setting for “JPEG File”. If you change, click “OK”. 10. Select “Jpeg2000 File” as a file format in the “Save as type” list box. 11. Click “Compression” to confirm the file compression setting for “Jpeg2000 File”. If you change, click “OK”. 12. Select “Depends on Image Type” in the “Save as type” list box. 13. “File Type Settings” dialog box appears and confirm the settings for each type. If you change, click “OK”. 14. Select “Jpeg File” as a file format in the “Save as type” list box. 15. Confirm the setting of File Name at the bottom right and click “Save”. -

Understanding Image Formats and When to Use Them
Understanding Image Formats And When to Use Them Are you familiar with the extensions after your images? There are so many image formats that it’s so easy to get confused! File extensions like .jpeg, .bmp, .gif, and more can be seen after an image’s file name. Most of us disregard it, thinking there is no significance regarding these image formats. These are all different and not cross‐ compatible. These image formats have their own pros and cons. They were created for specific, yet different purposes. What’s the difference, and when is each format appropriate to use? Every graphic you see online is an image file. Most everything you see printed on paper, plastic or a t‐shirt came from an image file. These files come in a variety of formats, and each is optimized for a specific use. Using the right type for the right job means your design will come out picture perfect and just how you intended. The wrong format could mean a bad print or a poor web image, a giant download or a missing graphic in an email Most image files fit into one of two general categories—raster files and vector files—and each category has its own specific uses. This breakdown isn’t perfect. For example, certain formats can actually contain elements of both types. But this is a good place to start when thinking about which format to use for your projects. Raster Images Raster images are made up of a set grid of dots called pixels where each pixel is assigned a color. -

Effects of JPEG2000 on the Information and Geometry Content of Aerial Photo Compression
03-082.qxd 1/11/05 5:17 PM Page 157 Effects of JPEG2000 on the Information and Geometry Content of Aerial Photo Compression Jung-Kuan Liu, Houn-Chien Wu, and Tian-Yuan Shih Abstract evaluated the effects of compression on geometric accuracy. Li The standardization effort of the next ISO standard for et al., (2002) indicated that when compression ratios are less compression of the still image, JPEG2000, has recently than a factor of 10, the compressed image is near-lossless with reached International Standard (IS) status. This wavelet- JPEG. In other words, the visual quality of JPEG compressed based standard outperforms the Discrete Cosine Transform images remains excellent and the accuracy of manual image (DCT) based JPEG in terms of compression ratio, as well mensuration is, essentially, not influenced. Paola et al. (1995) as, quality. In this study, the performance of JPEG2000 is and Schmanske and Loew (2001) concentrated on the classifi- evaluated for aerial image compressions. Different com- cation accuracies of compressed images. Paola et al. (1995) pression ratios are applied to scanned aerial photos at the revealed that high quality classifications could be obtained for 1:5 000 scale. Both the image quality measurements and the images with JPEG compression ratios approaching 10:1 or even accuracy of photogrammetric point determination aspects higher. The classification result retains its overall appearance, are examined. The evaluation of image quality is based but the smoothing effect of high compression tends to elimi- on visual analysis of the objects in the scene and on the nate much of the pixel-to-pixel detail. -

Image Formats
Image Formats Ioannis Rekleitis Many different file formats • JPEG/JFIF • Exif • JPEG 2000 • BMP • GIF • WebP • PNG • HDR raster formats • TIFF • HEIF • PPM, PGM, PBM, • BAT and PNM • BPG CSCE 590: Introduction to Image Processing https://en.wikipedia.org/wiki/Image_file_formats 2 Many different file formats • JPEG/JFIF (Joint Photographic Experts Group) is a lossy compression method; JPEG- compressed images are usually stored in the JFIF (JPEG File Interchange Format) >ile format. The JPEG/JFIF >ilename extension is JPG or JPEG. Nearly every digital camera can save images in the JPEG/JFIF format, which supports eight-bit grayscale images and 24-bit color images (eight bits each for red, green, and blue). JPEG applies lossy compression to images, which can result in a signi>icant reduction of the >ile size. Applications can determine the degree of compression to apply, and the amount of compression affects the visual quality of the result. When not too great, the compression does not noticeably affect or detract from the image's quality, but JPEG iles suffer generational degradation when repeatedly edited and saved. (JPEG also provides lossless image storage, but the lossless version is not widely supported.) • JPEG 2000 is a compression standard enabling both lossless and lossy storage. The compression methods used are different from the ones in standard JFIF/JPEG; they improve quality and compression ratios, but also require more computational power to process. JPEG 2000 also adds features that are missing in JPEG. It is not nearly as common as JPEG, but it is used currently in professional movie editing and distribution (some digital cinemas, for example, use JPEG 2000 for individual movie frames). -

About Graphics/Digital Images
About Graphics/Digital Images Digital images are found in lots of file formats (types) that are used for various reasons. I liken the file formats to flavors of ice-cream, which you might or might not choose to consume on any given day. One day chocolate is more important than mint; another day you might use vanilla, and on another day you might decide to combine more than one flavor in the same bowl. Likewise, you might choose one type of graphic file for a particular project, but it might be completely inappropriate for another project. What works well for display purposes (keeping it on the computer, or for publication to the internet) might not print well. Something that prints well might be too big a file to post to the internet, or may make your program run too slowly. Also, some authoring programs (like Boardmaker or Classroom Suite) might be written to only understand certain types of image files. Some file types are more common than others, and are more likely to be recognized by the “parent” program (the one you use to display, edit or print your image). Whatever type you pick ultimately depends on how you plan to use the image. The more technical definitions provided below are taken from the glossary found at http://www.photoshopelementsuser.com/glossary.php?letter=B The additional comments I have added, and hopefully let you know why you would care about any of this, anyway. The two biggest types of images I describe here fall loosely into two categories: vector images and bitmap images. -

Package 'Tiff'
Package ‘tiff’ March 31, 2021 Version 0.1-8 Title Read and Write TIFF Images Author Simon Urbanek <[email protected]> [aut, cre], Kent Johnson <[email protected]> [ctb] Maintainer Simon Urbanek <[email protected]> Depends R (>= 2.9.0) Description Functions to read, write and display bitmap images stored in the TIFF for- mat. It can read and write both files and in-memory raw vectors, including native image repre- sentation. License GPL-2 | GPL-3 SystemRequirements tiff and jpeg libraries URL https://www.rforge.net/tiff/ NeedsCompilation yes Repository CRAN Date/Publication 2021-03-31 15:10:02 UTC R topics documented: readTIFF . .1 writeTIFF . .4 Index 6 readTIFF Read a bitmap image stored in the TIFF format Description Reads an image from a TIFF file/content into a raster array. 1 2 readTIFF Usage readTIFF(source, native = FALSE, all = FALSE, convert = FALSE, info = FALSE, indexed = FALSE, as.is = FALSE, payload = TRUE) Arguments source Either name of the file to read from or a raw vector representing the TIFF file content. native logical, determines the image representation - if FALSE (the default) then the result is an array, if TRUE then the result is a native raster representation (suitable for plotting). all logical scalar or integer vector. TIFF files can contain more than one image. If all=TRUE then all images are returned in a list of images. If all is a vector, it gives the (1-based) indices of images to return. Otherwise only the first image is returned. convert logical, if TRUE then first convert the image into 8-bit RGBA samples and then to an array, see below for details. -

Graphics File Formats
Autumn 2016 CSCU9N5: Multimedia and HCI 1 Graphics File Formats Why have a range of graphics file formats? What to look for when choosing a file format A sample tour of different file formats, including – bitmap-based formats – vector-based formats – metafiles – proprietary formats Autumn 2016 CSCU9N5: Multimedia and HCI 2 1 Graphics File Formats Need to store and retrieve graphical data in an efficient and logical way – Data stored according to specific format conventions – Formats are immortal - technology evolves, new formats appear, but the old ones will still be there – No one universal format - different formats for different purposes – You (probably) won ’t need to access the formats in detail • there is usually library code to input/output/convert images for you – Useful to understand what is going on “behind the scenes ”, for making the best image format choices Autumn 2016 CSCU9N5: Multimedia and HCI 3 What to Look For in File Formats When choosing which is more appropriate for your purpose, some common factors to consider: – Lossy or lossless compression? – What is the compression ratio? – Data format: 8-bit (binary) or 7-bit (text)? – Is the image stored at a fixed resolution? – How many images per file (static or animated)? – Colour model? (usually RGB) – ….amongst other things Autumn 2016 CSCU9N5: Multimedia and HCI 4 2 Bitmaps Simplified structure of a bitmap file: Header Information File type, version, image size, compression method Palette Bitmap Data Usually in a compressed encoding In practice there are many format variations -

JP2 Format Preservation Assessment
Digital Date: 03/09/2015 Preservation Assessment: Preservation JP2 Format Team Version: 1.3 Document History Date Version Author(s) Circulation 10/12/2014 1.1 Paul Wheatley, Peter May, External Maureen Pennock 23/02/2015 1.2 Peter May External 03/09/2015 1.3 Simon Whibley External British Library Digital Preservation Team [email protected] This work is licensed under the Creative Commons Attribution 4.0 International License. Page 1 of 10 Digital Date: 03/09/2015 Preservation Assessment: Preservation JP2 Format Team Version: 1.3 1. Introduction This document provides a high level, non-collection specific assessment of the JP2 file format with regard to preservation risks and the practicalities of preserving data in this format. This format assessment is one of a series of assessments carried out by the British Library’s Digital Preservation Team. An explanation of criteria used in this assessment is provided in italics below each heading. 1.1 Scope This document will primarily focus on JP2 (JPEG2000 Part 1, core coding system) defined by ISO/IEC 15444-1:2000, but will reference other parts of the JPEG2000 standard(s) where context is necessary. A separate (or extended) assessment for JPX1 and JPM2, and indeed Motion JPEG2000 (Part 3), may be necessary depending on British Library needs. Issues of both preserving deposited JP2s and preserving JP2s created by the British Library as part of digitisation activities will be considered. Note that this assessment considers format issues only, and does not explore other factors essential to a preservation planning exercise, such as collection specific characteristics, that should always be considered before implementing preservation actions. -

Digital Preservation Guidance Note: Graphics File Formats
Digital Preservation Guidance Note: 4 Graphics File Formats Digital Preservation Guidance Note 4: Graphics file formats Document Control Author: Adrian Brown, Head of Digital Preservation Research Document Reference: DPGN-04 Issue: 2 Issue Date: August 2008 ©THE NATIONAL ARCHIVES 2008 Page 2 of 15 Digital Preservation Guidance Note 4: Graphics file formats Contents 1 INTRODUCTION .....................................................................................................................4 2 TYPES OF GRAPHICS FORMAT........................................................................................4 2.1 Raster Graphics ...............................................................................................................4 2.1.1 Colour Depth ............................................................................................................5 2.1.2 Colour Spaces and Palettes ..................................................................................5 2.1.3 Transparency............................................................................................................6 2.1.4 Interlacing..................................................................................................................6 2.1.5 Compression ............................................................................................................7 2.2 Vector Graphics ...............................................................................................................7 2.3 Metafiles............................................................................................................................7