A Comparative Analysis of Number Sense Instruction in Reform-Based and Traditional Mathematics Textbooks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter 13 National Science Foundation Systemic Initiatives
Chapter 13 National Science Foundation Systemic Initiatives: How a small amount of federal money promotes ill-designed mathematics and science programs in K-12 and undermines local control of education Michael McKeown Mathematically Correct David Klein California State University, Los Angeles Chris Patterson Education Connection of Texas Since its inception in 1950, the National Science Foundation (NSF) has played a strong, positive role in making American scientific research and technological application the best in the world. Through its funding of peer-reviewed, investigator-initiated research proposals, it has supported basic research in a wide variety of scientific disciplines, such as mathematics, biology, physics, chemistry, geology, astronomy, and psychology. American science owes much to the support it has received, and continues to receive, from NSF. This chapter deals with a program in the Education and Human Resources Division called the NSF Systemic Initiatives Program, not with NSF programs related directly to the support of basic research. We are highly critical of this particular NSF program. Not only do the Systemic Initiatives undermine local control of education, but, as our analysis in this chapter suggests, they also seem to lower academic standards for mathematics education and weaken the educational base for American science. This chapter is composed of three sections. The first section, an overview of NSF Systemic Initiatives, was written by Michael McKeown. The second section, an analysis of the development and 288 Standards Wars features of the Los Angeles Systemic Initiative, was written by David Klein. The third section, an analysis of the development and features of the Texas Statewide Systemic Initiative, was written by Chris Patterson. -

Mathematics in African History and Cultures
Paulus Gerdes & Ahmed Djebbar MATHEMATICS IN AFRICAN HISTORY AND CULTURES: AN ANNOTATED BIBLIOGRAPHY African Mathematical Union Commission on the History of Mathematics in Africa (AMUCHMA) Mathematics in African History and Cultures Second edition, 2007 First edition: African Mathematical Union, Cape Town, South Africa, 2004 ISBN: 978-1-4303-1537-7 Published by Lulu. Copyright © 2007 by Paulus Gerdes & Ahmed Djebbar Authors Paulus Gerdes Research Centre for Mathematics, Culture and Education, C.P. 915, Maputo, Mozambique E-mail: [email protected] Ahmed Djebbar Département de mathématiques, Bt. M 2, Université de Lille 1, 59655 Villeneuve D’Asq Cedex, France E-mail: [email protected], [email protected] Cover design inspired by a pattern on a mat woven in the 19th century by a Yombe woman from the Lower Congo area (Cf. GER-04b, p. 96). 2 Table of contents page Preface by the President of the African 7 Mathematical Union (Prof. Jan Persens) Introduction 9 Introduction to the new edition 14 Bibliography A 15 B 43 C 65 D 77 E 105 F 115 G 121 H 162 I 173 J 179 K 182 L 194 M 207 N 223 O 228 P 234 R 241 S 252 T 274 U 281 V 283 3 Mathematics in African History and Cultures page W 290 Y 296 Z 298 Appendices 1 On mathematicians of African descent / 307 Diaspora 2 Publications by Africans on the History of 313 Mathematics outside Africa (including reviews of these publications) 3 On Time-reckoning and Astronomy in 317 African History and Cultures 4 String figures in Africa 338 5 Examples of other Mathematical Books and 343 -

An Alternative Route to Teaching Fraction Division: Abstraction of Common Denominator Algorithm
International Electronic Journal of Elementary Education, 2015, 7(3), 399-422. An Alternative Route to Teaching Fraction Division: Abstraction of Common Denominator Algorithm İsmail Özgür ZEMBAT Mevlana (Rumi) University, Turkey Received: February 2015 / Revised: May 2015 / Accepted: May 2015 Abstract From a curricular stand point, the traditional invert and multiply algorithm for division of fractions provides few affordances for linking to a rich understanding of fractions. On the other hand, an alternative algorithm, called common denominator algorithm, has many such affordances. The current study serves as an argument for shifting curriculum for fraction division from use of invert and multiply algorithm as a basis to the use of common denominator algorithm as a basis. This was accomplished with the analysis of learning of two prospective elementary teachers being an illustration of how to realize those conceptual affordances. In doing so, the article proposes an instructional sequence and details it by referring to both the (mathematical and pedagogical) advantages and the disadvantages. As a result, this algorithm has a conceptual basis depending on basic operations of partitioning, unitizing, and counting, which make it accessible to learners. Also, when participants are encouraged to construct this algorithm based on their work with diagrams, common denominator algorithm formalizes the work that they do with diagrams. Keywords: Teaching fraction division, abstracting common denominator algorithm, curriculum development Introduction Arithmetic operations, and teaching and learning of them have always been an interest for mathematics education community. In his historical analysis, Usiskin (2007) pointed out that operations (especially on fractions) still preserve its importance in school mathematics and they should be given enough emphasis. -

AVAILABLE from ABSTRACT DOCUMENT RESUME Exemplary
DOCUMENT RESUME ED 434 033 SE 062 877 TITLE Exemplary and Promising Mathematics Programs. INSTITUTION Department of Education, Washington, DC. PUB DATE 1999-00-00 NOTE 71p.; Prepared by the "Math and Science Education Expert Panel." AVAILABLE FROM ED Pubs, P.O. Box 1389, Jessup, MD. Tel: 877-433-7827 (Toll Free); Web site: <http://www.enc.org>. PUB TYPE Reports Descriptive (141) EDRS PRICE MF01/PC03 Plus Postage. DESCRIPTORS *Academic Standards; Demonstration Programs; Elementary Secondary Education; Mathematics Curriculum; *Mathematics Education; *Program Descriptions; *Program Evaluation ABSTRACT Selecting programs, textbooks, and curriculum materials is one of the most important decisions educators make. An Expert Panel on Mathematics and Science was established by the U.S. Department of Education to develop a high-quality, research-based process for selecting programs and to use that selecting process to identify exemplary and promising programs. This booklet describes eight mathematics programs designated as exemplary or promising. A detailed explanation of the submission and selection process and an explanation of how the programs were separated into exemplary and promising categories is included. The four characteristics used for the selection criteria include quality of program, usefulness to others, educational significance, and evidence of effectiveness and success. Each characteristic has multiple criteria with specific indicators of achievement. Each program is described in terms of the four selection characteristics and professional -

The Impact of Information and Communication Technology on Our Understanding of the Nature of Mathematics
FLM 26(1) 2/2/06 12:33 PM Page 29 THE IMPACT OF INFORMATION AND COMMUNICATION TECHNOLOGY ON OUR UNDERSTANDING OF THE NATURE OF MATHEMATICS FREDERICK K. S. LEUNG The incorporation of information and communication tech- scientific calculator) and it can also be used as a transforma- nology (ICT) into mathematics education constitutes one of tional tool, a data collection and analysis tool, a visualizing the most important themes in contemporary mathematics tool and/or a checking tool. Doerr and Zangor (2000) sum- education. For example, one of the six principles of school marized the different roles the graphing calculator plays and mathematics as espoused by the National Council of Teach- the corresponding student actions as follows: ers of Mathematics (NCTM, 2000) is that Role of the Description of Student Actions Technology is essential in teaching and learning math- Graphing Calculator ematics; it influences the mathematics that is taught and enhances students’ learning. (p. 24, emphasis added). Computational Tool Evaluating numerical expressions, esti- mating and rounding The purpose of this article is to review research findings on the effectiveness of the use of some selected ICT tools in Transformational Tool Changing the nature of the task mathematics teaching and learning. [1] This review is then Data Collection and Gathering data, controlling phenomena, set against a summary of the actual use of ICT tools in real Analysis Tool fiding patterns classrooms. Various issues related to the incorporation of Visualizing Tool Finding symbolic functions, displaying ICT into mathematics education arise, including: data, interpreting data, solving equations • the reasons for the discrepancy between the poten- Checking Tool Confirming conjectures, understanding tial and actual use of ICT multiple symbolic forms Figure 1: Table showing the patterns and modes of use of a • the impact of ICT on our understanding of the graphing calculator (p. -

Traditional Mathematics Teaching Is Still the Norm in Our Nation's Schools
Forum on Public Policy Mathematics and Literature: Educators’ Perspectives on Utilizing a Reformative Approach to Bridge Two Cultures Suzanne J. Nesmith, Associate Dean/Assistant Professor of Education, Wayland Baptist University Abstract The existence of two distinct cultures within our society, the arts and the sciences, was introduced by physicist C. P. Snow in his 1959 Reed Lecture at Cambridge University and was further illuminated by Snow in The Two Cultures, a Second Look (1964). Lamenting the existence of the cultural chasm while also fearing a widening of the schism, Snow opened a dialogue with the hope of reconciliation between the cultures. Fifty years later, although the chasm still exists, numerous entities and individuals within the cultures work to formulate the means by which the cultures may be bridged, and, subsequently, the chasm narrowed and eliminated. The National Council of Teachers of Mathematics (NCTM) is one such entity, and leaders of the group have worked since the council‟s establishment in 1920 to research, promote, and improve the teaching and learning of mathematics through innovative, reformative approaches. Reform-oriented curricula are built upon constructivist perspectives aimed at assisting students in utilizing their own unique backgrounds and experiences to develop a personal understanding of mathematical situations. One means of infusing personal experience into the mathematics curriculum, while also bridging the aforementioned cultures, is through the incorporation of children‟s literature, yet there exists great variance in the type, format, structure, and success of the methodology‟s implementation. Subsequently, while the reformative approach of mathematics literature integration presents as a means of building understanding by bridging the cultures of mathematics and the humanities, it is the educator‟s choices relevant to the approach which have the greatest impact on the outcomes of the approach. -

The Comparison of Physical/Virtual Manipulative on Fifth-Grade Students’ Understanding of Adding Fractions
Running Head: COMPARISON OF PHYSICAL/VIRTUAL MANIPULATIVE The Comparison of Physical/Virtual Manipulative on Fifth-Grade Students’ Understanding of Adding Fractions A dissertation submitted to the Graduate School of the University of Cincinnati in partial fulfillment of the requirements for the degree of Doctor of Education in the Department of Curriculum and Instruction of the College of Education by Sami Alshehri M.A. Umm Al-Qura University July 2008 Committee Chair: M. Sally, Ed.D. COMPARISON OF PHYSICAL/VIRTUAL MANIPULATIVE ABSTRACT The purpose of this quantitative study was to compare two types of manipulatives in order to see their effects upon understanding of adding fractions for three comparable groups of fifth grade students. A total of 163 students who demonstrated low mathematical performance participated in the project in order to learn the addition of fractions by using physical and virtual manipulatives for the experimental groups and the normal mathematic curriculum for the control group. The intervention occurred during a two-week time frame in six public elementary schools in Abha, Saudi Arabia where students used fraction bars for both physical and virtual manipulatives in order to build conceptual understanding of adding fractions properly. Instructions were provided to all the participants directly regarding what the participants were to do each day of the 2-week experiment. Pre-and post-tests, an attitude survey, and a preference survey were the instruments that were used to collect data during the study. A repeated measures design with a cross over treatment was used for comparing the effects of the two modes of treatments, virtual and physical manipulatives, compared to a control group for the understanding of adding fractions for the three groups of students. -

The Use Or Non-Use of Calculators Affects on Student's Ability to Perform Basic Mathematics Problems
Old Dominion University ODU Digital Commons OTS Master's Level Projects & Papers STEM Education & Professional Studies 2008 The Use or Non-Use of Calculators Affects on Student's Ability to Perform Basic Mathematics Problems Christina Miles Old Dominion University Follow this and additional works at: https://digitalcommons.odu.edu/ots_masters_projects Part of the Education Commons Recommended Citation Miles, Christina, "The Use or Non-Use of Calculators Affects on Student's Ability to Perform Basic Mathematics Problems" (2008). OTS Master's Level Projects & Papers. 89. https://digitalcommons.odu.edu/ots_masters_projects/89 This Master's Project is brought to you for free and open access by the STEM Education & Professional Studies at ODU Digital Commons. It has been accepted for inclusion in OTS Master's Level Projects & Papers by an authorized administrator of ODU Digital Commons. For more information, please contact [email protected]. THE USE OR NON-USE OF CALCULATORS AFFECTS ON STUDENT’S ABILITY TO PERFORM BASIC MATHEMATICS PROBLEMS A RESEARCH PAPER PRESENTED TO THE GRADUATE FACULTY OF THE DEPARTMENT OF OCCUPATIONAL AND TECHNICAL EDUCATION STUDIES AT OLD DOMINION UNIVERSITY IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE MASTER OF SCIENCE DEGREE BY CHRISTINA GORDON MILES AUGUST 2008 ii APPROVAL PAGE This research paper was prepared by Christina Gordon Miles under the direction of Dr. John Ritz at Old Dominion University in Norfolk, Virginia. It was submitted to the Graduate Program Director as partial fulfillment of the requirements for the Degree of Master of Science. APPROVAL BY: _____________________________ Date _______________________ Dr. John M. Ritz Advisor and Graduate Program Director iii ACKNOWLEDGEMENTS I would like to especially thank my husband, Captain Paul E. -

The Effects of Changing from a Traditional Mathematics Curriculum to an Integrated Mathematics Curriculum on Student Mathematics Learning in Georgia
The University of Southern Mississippi The Aquila Digital Community Dissertations Fall 12-2011 The Effects of Changing from a Traditional Mathematics Curriculum to an Integrated Mathematics Curriculum on Student Mathematics Learning in Georgia Catherine Lynn Mallanda University of Southern Mississippi Follow this and additional works at: https://aquila.usm.edu/dissertations Part of the Curriculum and Instruction Commons, Educational Assessment, Evaluation, and Research Commons, and the Elementary and Middle and Secondary Education Administration Commons Recommended Citation Mallanda, Catherine Lynn, "The Effects of Changing from a Traditional Mathematics Curriculum to an Integrated Mathematics Curriculum on Student Mathematics Learning in Georgia" (2011). Dissertations. 485. https://aquila.usm.edu/dissertations/485 This Dissertation is brought to you for free and open access by The Aquila Digital Community. It has been accepted for inclusion in Dissertations by an authorized administrator of The Aquila Digital Community. For more information, please contact [email protected]. The University of Southern Mississippi THE EFFECTS OF CHANGING FROM A TRADITIONAL MATHEMATICS CURRICULUM TO AN INTEGRATED MATHEMATICS CURRICULUM ON STUDENT MATHEMATICS LEARNING IN GEORGIA by Catherine Lynn Mallanda Abstract of a Dissertation Submitted to the Graduate School of The University of Southern Mississippi in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy December 2011 ABSTRACT THE EFFECTS OF CHANGING FROM A TRADITIONAL MATHEMATICS CURRICULUM TO AN INTEGRATED MATHEMATICS CURRICULUM ON STUDENT MATHEMATICS LEARNING IN GEORGIA by Catherine Lynn Mallanda December 2011 In 2005, the state of Georgia adopted a new integrated mathematics curriculum, the Georgia Performance Standards (GPS), which included a task-based approach for instruction. -

What Students Notice As Different Between Reform and Traditional Mathematics Programs
Journal for Research in Mathematics Education 2008, Vol. 39, No. 1, 9–32 What Students Notice as Different Between Reform and Traditional Mathematics Programs Jon R. Star Harvard University John P. Smith III Michigan State University Amanda Jansen University of Delaware Research on the impact of Standards-based mathematics and reform calculus curricula has largely focused on changes in achievement and attitudes, generally ignoring how students experience these new programs. This study was designed to address that deficit. As part of a larger effort to characterize students’ transitions into and out of reform programs, we analyzed how 93 high school and college students perceived Standards-based and reform calculus programs as different from traditional ones. Results show considerable diversity across and even within sites. Nearly all students reported differences, but high-impact differences, like Content, were not always related to curriculum type (reform or traditional). Students’ perceptions aligned moderately well with those of reform curriculum authors, e.g., concerning Typical Problems. These results show that students’ responses to reform programs can be quite diverse and only partially aligned with adults’ views. Key words: College/university; Curriculum; High school (9–12); Integrated curriculum; Learners (characteristics of); Qualitative methods; Reform in mathematics education; Social factors One inevitable outcome of the development of new curricula in any field, but perhaps particularly in mathematics, is to provoke discussion and debate about what content can and should be taught in schools and universities. The recent cycle of The entire Mathematical Transitions Project team played a vital role in the work reported here. In addition to the authors, the other members of this team were, in alphabetical order, Dawn Berk, Carol Burdell, Beth Herbel-Eisenmann, Gary Lewis, and Violeta Rosca-Yurita. -
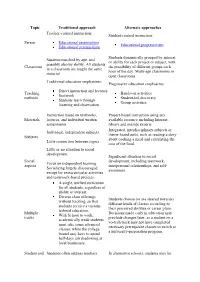
Topic Traditional Approach Alternate Approaches Person
Topic Traditional approach Alternate approaches Teacher-centred instruction: Student-centred instruction: Person Educational essentialism Educational progressivism Educational perennialism Students dynamically grouped by interest Students matched by age, and or ability for each project or subject, with possibly also by ability. All students Classroom the possibility of different groups each in a classroom are taught the same hour of the day. Multi-age classrooms or material. open classrooms. Traditional education emphasizes: Progressive education emphasizes: Direct instruction and lectures Teaching Hands-on activities Seatwork methods Student-led discovery Students learn through Group activities listening and observation Instruction based on textbooks, Project-based instruction using any Materials lectures, and individual written available resource including Internet, assignments library and outside experts Integrated, interdisciplinary subjects or Individual, independent subjects. theme-based units, such as reading a story Subjects about cooking a meal and calculating the Little connection between topics cost of the food. Little or no attention to social development. Significant attention to social Social development, including teamwork, Focus on independent learning. aspects interpersonal relationships, and self- Socializing largely discouraged awareness. except for extracurricular activities and teamwork-based projects. A single, unified curriculum for all students, regardless of ability or interest. Diverse class offerings Students choose (or are steered towards) without tracking, so that different kinds of classes according to students receive a custom- their perceived abilities or career plans. tailored education. Multiple Decisions made early in education may With School to work, tracks preclude changes later, as a student on a academically weak students vo-tech track may not have completed must take some advanced necessary prerequisite classes to switch to classes, while the college a university-preparation program. -

Direct Instruction in Mathematics: Issues for Schools with High Indigenous Enrolments: a Literature Review Bronwyn Ewing [email protected]
Australian Journal of Teacher Education Volume 36 | Issue 5 Article 6 2011 Direct Instruction In Mathematics: Issues For Schools With High Indigenous Enrolments: A Literature Review Bronwyn Ewing [email protected] Recommended Citation Ewing, Bronwyn (2011) "Direct Instruction In Mathematics: Issues For Schools With High Indigenous Enrolments: A Literature Review," Australian Journal of Teacher Education: Vol. 36: Iss. 5, Article 6. Available at: http://ro.ecu.edu.au/ajte/vol36/iss5/6 This Journal Article is posted at Research Online. http://ro.ecu.edu.au/ajte/vol36/iss5/6 Australian Journal of Teacher Education Direct Instruction In Mathematics: Issues For Schools With High Indigenous Enrolments: A Literature Review Bronwyn Ewing Queensland University of Technology [email protected] Abstract: Direct instruction, an approach that is becoming familiar to Queensland schools that have high Aboriginal and Torres Strait Islander populations, has been gaining substantial political and popular support in the United States of America [USA], England and Australia. Recent examples include the No Child Left Behind policy in the USA, the British National Numeracy Strategy and in Australia, Effective Third Wave Intervention Strategies. Direct instruction, stems directly from the model created in the 1960s under a Project Follow Through grant. It has been defined as a comprehensive system of education involving all aspects of instruction. Now in its third decade of influencing curriculum, instruction and research, direct instruction is also into its third decade of controversy because of its focus on explicit and highly directed instruction for learning. Characteristics of direct instruction are critiqued and discussed to identify implications for teaching and learning for Indigenous students.