Lift and Wakes of Flying Snakes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Physical Mechanisms of Control of Gliding in Flying Snakes
Physical Mechanisms of Control of Gliding in Flying Snakes Farid Jafari Dissertation submitted to the faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Engineering Mechanics John J. Socha, chair Nicole Abaid Shane D. Ross Pavlos P. Vlachos Craig A. Woolsey August 12, 2016 Blacksburg, VA Keywords: Flying snakes, glide, stability, control, and aerodynamics Physical Mechanisms of Control of Gliding in Flying Snakes Farid Jafari ABSTRACT Flying snakes possess a sophisticated gliding ability with a unique aerial behavior, in which they flatten their body to make a roughly triangular cross-sectional shape to produce lift and gain horizontal acceleration. Also, the snakes assume an S-like posture and start to undulate by sending traveling waves down the body. The present study aims to answer how the snakes are able to control their glide trajectory and remain stable without any specialized flight surfaces. Undulation is the most prominent behavior of flying snakes and is likely to influence their dynamics and stability. To examine the effects of undulation, a number of theoretical models were used. First, only the longitudinal dynamics were considered with simple two-dimensional models, in which the snake was approximated as a number of connected airfoils. Previously measured force coefficients were used to model aerodynamic forces, and undulation was considered as periodic changes in the mass and area of the airfoils. The model was shown to be passively unstable, but it could be stabilized with a restoring pitching moment. Next, a three- dimensional model was developed, with the snake modeled as a chain of airfoils connected through revolute joints, and undulation was considered as periodic changes in the joint angles. -

SR 55(4) 42-44.Pdf
FEATURE ARTICLE Oriental fl ying gurnard (Dactyloptera orientalis) Carribean fl ying gurnard (Dactyloptera volitans) Fliers Without Prafulla Kumar Mohanty Four-winged fl ying fi sh Feathers & Damayanti Nayak (Cypselurus californicus) LIGHT is an amazing 2. Flying squid: In the Flying squid accomplishment that evolved (Todarodes pacifi cus), commonly Ffi rst in the insects and was called Japanese fl ying squid, the mantle observed subsequently up to the encloses the visceral mass of the squid, mammalian class. However, the word and has two enlarged lateral fi ns. The ‘fl ying’ brings to mind pictures of birds squid has eight arms and two tentacles only. with suction cups along the backs. But there are many other fl yers other In between the arms sits the mouth, than birds in the animal kingdom who inside the mouth a rasping organ called have mastered the art of being airborne. radula is present. Squids have ink sacs, Japanese fl ying squid Different body structures and peculiar which they use as a defence mechanism organs contribute to the aerodynamic against predators. Membranes are stability of these organisms. Let’s take present between the tentacles. They 40 cm in length respectively. When a look at some of them. can fl y more than 30 m in 3 seconds they leave water for the air, sea birds uniquely utilising their jet-propelled such as frigates, albatrosses, and gulls aerial locomotion. 1. Gliding ant: Gliding ants are liable to attack. Its body lifts above (Cephalotes atrautus) are arboreal ants the surface, it spread its fi ns and taxis 3. -

Locomotion of Reptiles" Will Be of Interest to a Wide Range of Readers
REVIEW A RTICLES Editorial note. We are trying to introduce a "new look" to the BHS Bulletin, and one of our plans is to commission articles by well-known zoologists summarising recent advances in their area of expertise, as they relate to herpetology. We are particularly pleased that Professor McNeill Alexander of Leeds University agreed to write the first of these. We hope that this masterly summary of "Locomotion of Reptiles" will be of interest to a wide range of readers. Roger Meek and Roger Avery, Co-Editors. Locomotion of Reptiles R. McNEILL ALEXANDER Institute for Integrative and Comparative Biology, University of Leeds, Leeds LS2 9JT, UK. [email protected] ABSTRACT – Reptiles run, crawl, climb, jump, glide and swim. Exceptional species run on the surface of water or “swim” through dry sand. This paper is a short summary of current knowledge of all these modes of reptilian locomotion. Most of the examples refer to lizards or snakes, but chelonians and crocodilians are discussed briefly. Extinct reptiles are omitted. References are given to scientific papers that provide more detailed information. INTRODUCTION the body and the leg joints much straighter, as in his review is an attempt to explain briefly elephants. The bigger an animal is, the harder it Tthe many different modes of locomotion that is for them to support the weight of the body in a reptiles use. Some of the information it gives lizard-like stance. Imagine two reptiles of exactly has been known for many years, but many of the the same shape, one twice as long as the other. -

A Rapid Survey of Online Trade in Live Birds and Reptiles in The
S H O R T R E P O R T 0ൾඍඁඈൽඌ A rapid online survey was undertaken EHWZHHQDQG)HEUXDU\ GD\V DSSUR[LPDWHO\KRXUVVXUYH\GD\ RQ pre-selected Facebook groups specializing in the trade of live pets. Ten groups each for reptiles and birds were selected based on trading activities in the previous six months. The survey was carried out during ZHHN GD\V 0RQGD\ WR )ULGD\ E\ JRLQJ through each advertisement posted in A rapid survey of online trade in the groups. Information, including that live birds and reptiles in the Philippines relating to species, quantity, and asking HYDROSAURUS PUSTULATUS WWF / URS WOY WOY WWF / URS PUSTULATUS HYDROSAURUS SULFH ZDV QRWHG 6SHFLHV ZHUH LGHQWL¿HG Report by Cristine P. Canlas, Emerson Y. Sy, to the lowest taxonomic level whenever and Serene Chng possible. Taxonomy follows Gill and 'RQVNHU IRU ELUGV DQG 8HW] et al. IRUUHSWLOHV7KHDXWKRUVFDOFXODWHG ,ඇඍඋඈൽඎർඍංඈඇ WKH WRWDO SRWHQWLDO YDOXH R൵HUHG IRU ELUGV and reptiles based on prices indicated he Philippines is the second largest archipelago in the world by traders. Advertisements that did not comprising 7641 islands and is both a mega-biodiverse specify prices were assigned the lowest country for harbouring wildlife species found nowhere known price for each taxon. Valuations in else in the world, and one of eight biodiversity hotspots this report were based on a conversion rate having a disproportionate number of species threatened with RI86' 3+3 $QRQ ,WLV ,//8675$7,213+,/,33,1(6$,/),1/,=$5' TH[WLQFWLRQIXUWKHULWKDVVRPHRIWKHKLJKHVWUDWHVRIHQGHPLFLW\LQWKH not always possible during online surveys world (Myers et al 7KHLOOHJDOZLOGOLIHWUDGHLVRQHRIWKHPDLQ WRYHULI\WKDWDOOR൵HUVDUHJHQXLQH UHDVRQVEHKLQGVLJQL¿FDQWGHFOLQHVRIVRPHZLOGOLIHSRSXODWLRQVLQ$VLD LQFOXGLQJWKH3KLOLSSLQHV $QRQ6RGKLet al1LMPDQDQG 5ൾඌඎඅඍඌ 6KHSKHUG'LHVPRVet al5DRet al 7KHWildlife Act of 2001 (Republic Act No. -

Research Journal of Pharmaceutical, Biological and Chemical
ISSN: 0975-8585 Research Journal of Pharmaceutical, Biological and Chemical Sciences Diversity of Squamates (Scaled Reptiles) in Selected Urban Areas of Cagayan de Oro City, Misamis Oriental. John C Naelga*, Daniel Robert P Tayag, Hazel L Yañez, and Astrid L Sinco. Xavier University – Ateneo De Cagayan, Kinaadman Resource Center. ABSTRACT This study was conducted to provide baseline information on the local urban diversity of squamates in the selected areas of Barangay Kauswagan, Barangay Balulang, and Barangay FS Catanico in Cagayan de Oro City. These urban sites are close to the river and are likely to be inhabited by reptiles. Each site had at least ten (10) points and was sampled no less than five (5) times in the months of September to November 2016 using homemade traps and the Cruising-Transect walk method. One representative per species was preserved. A total of two hundred sixty-seven (267) individuals, grouped into four (4) families and ten (10) species were found in the sampling areas. Six (6) snake species were identified, namely: Boiga cynodon, Naja samarensis, Chrysopelea paradisi, Gonyosoma oxycephalum, Coelegnathus erythrurus eryhtrurus, and Dendrelaphis pictus; while four (4) species were lizards namely: Gekko gecko, Hemidactylus platyurus, Lamprolepis smaragdina philippinica, and Eutropis multifasciata.In Barangay Kauswagan, Hemidactylus platyurus was the most abundant (RA= 52.94%). In Barangay Balulang, the most abundant species was Hemidactylus platyurus (RA= 43.82%). In Barangay FS Catanico, the most abundant was Hemidactylus platyurus (RA= 40.16%). The area with the highest species diversity was Barangay FS Catanico (H= 1.36), followed by Barangay Balulang (H= 1.28), and Barangay Kauswagan (H= 1.08). -
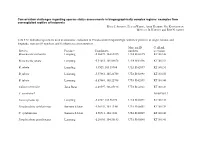
Conservation Challenges Regarding Species Status Assessments in Biogeographically Complex Regions: Examples from Overexploited Reptiles of Indonesia KYLE J
Conservation challenges regarding species status assessments in biogeographically complex regions: examples from overexploited reptiles of Indonesia KYLE J. SHANEY, ELIJAH WOSTL, AMIR HAMIDY, NIA KURNIAWAN MICHAEL B. HARVEY and ERIC N. SMITH TABLE S1 Individual specimens used in taxonomic evaluation of Pseudocalotes tympanistriga, with their province of origin, latitude and longitude, museum ID numbers, and GenBank accession numbers. Museum ID GenBank Species Province Coordinates numbers accession Bronchocela cristatella Lampung -5.36079, 104.63215 UTA R 62895 KT180148 Bronchocela jubata Lampung -5.54653, 105.04678 UTA R 62896 KT180152 B. jubata Lampung -5.5525, 105.18384 UTA R 62897 KT180151 B. jubata Lampung -5.57861, 105.22708 UTA R 62898 KT180150 B. jubata Lampung -5.57861, 105.22708 UTA R 62899 KT180146 Calotes versicolor Jawa Barat -6.49597, 106.85198 UTA R 62861 KT180149 C. versicolor* NC009683.1 Gonocephalus sp. Lampung -5.2787, 104.56198 UTA R 60571 KT180144 Pseudocalotes cybelidermus Sumatra Selatan -4.90149, 104.13401 UTA R 60551 KT180139 P. cybelidermus Sumatra Selatan -4.90711, 104.1348 UTA R 60549 KT180140 Pseudocalotes guttalineatus Lampung -5.28105, 104.56183 UTA R 60540 KT180141 P. guttalineatus Sumatra Selatan -4.90681, 104.13457 UTA R 60501 KT180142 Pseudocalotes rhammanotus Lampung -4.9394, 103.85292 MZB 10804 KT180147 Pseudocalotes species 4 Sumatra Barat -2.04294, 101.31129 MZB 13295 KT211019 Pseudocalotes tympanistriga Jawa Barat -6.74181, 107.0061 UTA R 60544 KT180143 P. tympanistriga Jawa Barat -6.74181, 107.0061 UTA R 60547 KT180145 Pogona vitticeps* AB166795.1 *Entry to GenBank by previous authors TABLE S2 Reptile species currently believed to occur Java and Sumatra, Indonesia, with IUCN Red List status, and certainty of occurrence. -

P. 1 AC27 Inf. 7 (English Only / Únicamente En Inglés / Seulement
AC27 Inf. 7 (English only / únicamente en inglés / seulement en anglais) CONVENTION ON INTERNATIONAL TRADE IN ENDANGERED SPECIES OF WILD FAUNA AND FLORA ____________ Twenty-seventh meeting of the Animals Committee Veracruz (Mexico), 28 April – 3 May 2014 Species trade and conservation IUCN RED LIST ASSESSMENTS OF ASIAN SNAKE SPECIES [DECISION 16.104] 1. The attached information document has been submitted by IUCN (International Union for Conservation of * Nature) . It related to agenda item 19. * The geographical designations employed in this document do not imply the expression of any opinion whatsoever on the part of the CITES Secretariat or the United Nations Environment Programme concerning the legal status of any country, territory, or area, or concerning the delimitation of its frontiers or boundaries. The responsibility for the contents of the document rests exclusively with its author. AC27 Inf. 7 – p. 1 Global Species Programme Tel. +44 (0) 1223 277 966 219c Huntingdon Road Fax +44 (0) 1223 277 845 Cambridge CB3 ODL www.iucn.org United Kingdom IUCN Red List assessments of Asian snake species [Decision 16.104] 1. Introduction 2 2. Summary of published IUCN Red List assessments 3 a. Threats 3 b. Use and Trade 5 c. Overlap between international trade and intentional use being a threat 7 3. Further details on species for which international trade is a potential concern 8 a. Species accounts of threatened and Near Threatened species 8 i. Euprepiophis perlacea – Sichuan Rat Snake 9 ii. Orthriophis moellendorfi – Moellendorff's Trinket Snake 9 iii. Bungarus slowinskii – Red River Krait 10 iv. Laticauda semifasciata – Chinese Sea Snake 10 v. -

Chrysopelea Ornata)
Material properties of skin in a flying snake (Chrysopelea ornata) Sarah Bonham Dellinger Thesis submitted to the faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Master of Science In Engineering Mechanics John J. Socha, Chair Raffaella De Vita Pavlos P. Vlachos April 27, 2011 Blacksburg, VA Keywords: flying snakes, skin, material properties, digital image correlation © Sarah Bonham Dellinger 2011 Material properties of skin in a flying snake (Chrysopelea ornata) Sarah Bonham Dellinger ABSTRACT The genus Chrysopelea encompasses the “flying” snakes. This taxon has the ability to glide via lateral aerial undulation and dorsoventral body flattening, a skill unique to this group, but in addition to other functions common to all colubrids. The skin must be extensible enough to allow this body shape alteration and undulation, and strong enough to withstand the forces seen during landing. For this reason, characterizing the mechanical properties of the skin may give insight to the functional capabilities of the skin during these gliding and landing behaviors. Dynamic and viscoelastic uniaxial tensile tests were combined with a modified particle image velocimetry technique to provide strength, extensibility, strain energy, and stiffness information about the skin with respect to orientation, region, and species, along with viscoelastic parameters. Results compared with two other species in this study and a broader range of species in prior studies indicate that while the skin of these unique snakes may not be specifically specialized to deal with larger forces, extensibility, or energy storage and release, the skin does have increased strength and energy storage associated with higher strain rates. -

Tangled Skeins: a First Report of Non-Captive Mating Behavior in the Southeast Asian Paradise Flying Snake (Reptilia: Squamata: Colubridae: Chrysopelea Paradisi)
OPEN ACCESS All articles published in the Journal of Threatened Taxa are registered under Creative Commons Attribution 4.0 Interna- tional License unless otherwise mentioned. JoTT allows unrestricted use of articles in any medium, reproduction and distribution by providing adequate credit to the authors and the source of publication. Journal of Threatened Taxa The international journal of conservation and taxonomy www.threatenedtaxa.org ISSN 0974-7907 (Online) | ISSN 0974-7893 (Print) Short Communication Tangled skeins: a first report of non-captive mating behavior in the Southeast Asian Paradise Flying Snake (Reptilia: Squamata: Colubridae: Chrysopelea paradisi) Hinrich Kaiser, Johnny Lim, Heike Worth & Mark O’Shea 26 February 2016 | Vol. 8 | No. 2 | Pp. 8488–8494 10.11609/jott.2440.8.2.8488-8494 For Focus, Scope, Aims, Policies and Guidelines visit http://threatenedtaxa.org/About_JoTT.asp For Article Submission Guidelines visit http://threatenedtaxa.org/Submission_Guidelines.asp For Policies against Scientific Misconduct visit http://threatenedtaxa.org/JoTT_Policy_against_Scientific_Misconduct.asp For reprints contact <[email protected]> Publisher/Host Partner Threatened Taxa Journal of Threatened Taxa | www.threatenedtaxa.org | 26 February 2016 | 8(2): 8488–8494 Tangled skeins: a first report of non-captive mating behavior in the Southeast Asian Paradise Flying Snake ISSN 0974-7907 (Online) (Reptilia: Squamata: Colubridae: Chrysopelea paradisi) Short Communication Short ISSN 0974-7893 (Print) Hinrich Kaiser 1, Johnny Lim 2, Heike -

First Record of Ahaetulla Mycterizans
Turkish Journal of Zoology Turk J Zool (2020) 44: 11-21 http://journals.tubitak.gov.tr/zoology/ © TÜBİTAK Research Article doi:10.3906/zoo-1904-1 First record of Ahaetulla mycterizans (Linnaeus, 1758) (Serpentes: Colubridae) from the Lesser Sunda region, Indonesia, based on molecular and morphological identification 1,2 1,3 4 1,2, Lilin Ika Nur INDAHSARI , Fatchiyah FATCHIYAH , Eric Nelson SMITH , Nia KURNIAWAN * 1 Department of Biology, Faculty of Mathematics and Natural Science, Brawijaya University, Malang, Indonesia 2 NK Research, Department of Biology, Faculty of Mathematics and Natural Science, Brawijaya University, Malang, Indonesia 3 Research Center of Smart Molecule of Natural Genetic Resources, Brawijaya University, Malang, Indonesia 4 Department of Biology, University of Texas at Arlington, Arlington, TX, USA Received: 01.04.2019 Accepted/Published Online: 25.11.2019 Final Version: 03.01.2020 Abstract: Previous studies on the distribution of the Ahaetulla snake across Indonesia only focused on morphological characters without any molecular data. This study was aimed at analyzing phylogenetic relationships among the genus Ahaetulla in Indonesia based on partial mitochondrial DNA sequences of 16 specimens collected from the Sundaland and Lesser Sunda regions. The 12S-rDNA gene was PCR-amplified and sequenced to analyze phylogenetic relationships and to estimate the divergence time between the 2 Ahaetulla populations of the Sundaland and Lesser Sunda regions. Morphological characters of 3 Ahaetulla specimens from Lesser Sunda and Sundaland have also been analyzed to confirm the results based on molecular markers. Both the phylogenetic analyses and morphological characters revealed the presence of 2 Ahaetulla species, A. mycterizans and A. -

Conservation of Amphibians and Reptiles in Indonesia: Issues and Problems
Copyright: © 2006 Iskandar and Erdelen. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and repro- Amphibian and Reptile Conservation 4(1):60-87. duction in any medium, provided the original author and source are credited. DOI: 10.1514/journal.arc.0040016 (2329KB PDF) The authors are responsible for the facts presented in this article and for the opinions expressed there- in, which are not necessarily those of UNESCO and do not commit the Organisation. The authors note that important literature which could not be incorporated into the text has been published follow- ing the drafting of this article. Conservation of amphibians and reptiles in Indonesia: issues and problems DJOKO T. ISKANDAR1 * AND WALTER R. ERDELEN2 1School of Life Sciences and Technology, Institut Teknologi Bandung, 10, Jalan Ganesa, Bandung 40132 INDONESIA 2Assistant Director-General for Natural Sciences, UNESCO, 1, rue Miollis, 75732 Paris Cedex 15, FRANCE Abstract.—Indonesia is an archipelagic nation comprising some 17,000 islands of varying sizes and geologi- cal origins, as well as marked differences in composition of their floras and faunas. Indonesia is considered one of the megadiversity centers, both in terms of species numbers as well as endemism. According to the Biodiversity Action Plan for Indonesia, 16% of all amphibian and reptile species occur in Indonesia, a total of over 1,100 species. New research activities, launched in the last few years, indicate that these figures may be significantly higher than generally assumed. Indonesia is suspected to host the worldwide highest numbers of amphibian and reptile species. -

A Biogeographic Synthesis of the Amphibians and Reptiles of Indochina
BAIN & HURLEY: AMPHIBIANS OF INDOCHINA & REPTILES & HURLEY: BAIN Scientific Publications of the American Museum of Natural History American Museum Novitates A BIOGEOGRAPHIC SYNTHESIS OF THE Bulletin of the American Museum of Natural History Anthropological Papers of the American Museum of Natural History AMPHIBIANS AND REPTILES OF INDOCHINA Publications Committee Robert S. Voss, Chair Board of Editors Jin Meng, Paleontology Lorenzo Prendini, Invertebrate Zoology RAOUL H. BAIN AND MARTHA M. HURLEY Robert S. Voss, Vertebrate Zoology Peter M. Whiteley, Anthropology Managing Editor Mary Knight Submission procedures can be found at http://research.amnh.org/scipubs All issues of Novitates and Bulletin are available on the web from http://digitallibrary.amnh.org/dspace Order printed copies from http://www.amnhshop.com or via standard mail from: American Museum of Natural History—Scientific Publications Central Park West at 79th Street New York, NY 10024 This paper meets the requirements of ANSI/NISO Z39.48-1992 (permanence of paper). AMNH 360 BULLETIN 2011 On the cover: Leptolalax sungi from Van Ban District, in northwestern Vietnam. Photo by Raoul H. Bain. BULLETIN OF THE AMERICAN MUSEUM OF NATURAL HISTORY A BIOGEOGRAPHIC SYNTHESIS OF THE AMPHIBIANS AND REPTILES OF INDOCHINA RAOUL H. BAIN Division of Vertebrate Zoology (Herpetology) and Center for Biodiversity and Conservation, American Museum of Natural History Life Sciences Section Canadian Museum of Nature, Ottawa, ON Canada MARTHA M. HURLEY Center for Biodiversity and Conservation, American Museum of Natural History Global Wildlife Conservation, Austin, TX BULLETIN OF THE AMERICAN MUSEUM OF NATURAL HISTORY Number 360, 138 pp., 9 figures, 13 tables Issued November 23, 2011 Copyright E American Museum of Natural History 2011 ISSN 0003-0090 CONTENTS Abstract.........................................................