Aas 20-488 Motion Primitives Summarizing Periodic Orbits And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Utilization of Halo Orbit§ in Advanced Lunar Operation§
NASA TECHNICAL NOTE NASA TN 0-6365 VI *o M *o d a THE UTILIZATION OF HALO ORBIT§ IN ADVANCED LUNAR OPERATION§ by Robert W. Fmqcbar Godddrd Spctce Flight Center P Greenbelt, Md. 20771 NATIONAL AERONAUTICS AND SPACE ADMINISTRATION WASHINGTON, D. C. JULY 1971 1. Report No. 2. Government Accession No. 3. Recipient's Catalog No. NASA TN D-6365 5. Report Date Jul;v 1971. 6. Performing Organization Code 8. Performing Organization Report No, G-1025 10. Work Unit No. Goddard Space Flight Center 11. Contract or Grant No. Greenbelt, Maryland 20 771 13. Type of Report and Period Covered 2. Sponsoring Agency Name and Address Technical Note J National Aeronautics and Space Administration Washington, D. C. 20546 14. Sponsoring Agency Code 5. Supplementary Notes 6. Abstract Flight mechanics and control problems associated with the stationing of space- craft in halo orbits about the translunar libration point are discussed in some detail. Practical procedures for the implementation of the control techniques are described, and it is shown that these procedures can be carried out with very small AV costs. The possibility of using a relay satellite in.a halo orbit to obtain a continuous com- munications link between the earth and the far side of the moon is also discussed. Several advantages of this type of lunar far-side data link over more conventional relay-satellite systems are cited. It is shown that, with a halo relay satellite, it would be possible to continuously control an unmanned lunar roving vehicle on the moon's far side. Backside tracking of lunar orbiters could also be realized. -

Astrodynamics
Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities -

Rendezvous Design in a Cislunar Near Rectilinear Halo Orbit Emmanuel Blazquez, Laurent Beauregard, Stéphanie Lizy-Destrez, Finn Ankersen, Francesco Capolupo
Rendezvous Design in a Cislunar Near Rectilinear Halo Orbit Emmanuel Blazquez, Laurent Beauregard, Stéphanie Lizy-Destrez, Finn Ankersen, Francesco Capolupo To cite this version: Emmanuel Blazquez, Laurent Beauregard, Stéphanie Lizy-Destrez, Finn Ankersen, Francesco Capolupo. Rendezvous Design in a Cislunar Near Rectilinear Halo Orbit. International Symposium on Space Flight Dynamics (ISSFD), Feb 2019, Melbourne, Australia. pp.1408-1413. hal-03200239 HAL Id: hal-03200239 https://hal.archives-ouvertes.fr/hal-03200239 Submitted on 16 Apr 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Open Archive Toulouse Archive Ouverte (OATAO) OATAO is an open access repository that collects the wor of some Toulouse researchers and ma es it freely available over the web where possible. This is an author's version published in: h ttps://oatao.univ-toulouse.fr/22865 To cite this version : Blazquez, Emmanuel and Beauregard, Laurent and Lizy-Destrez, Stéphanie and Ankersen, Finn and Capolupo, Francesco Rendezvous Design in a Cislunar Near Rectilinear Halo Orbit. -

A Hot Subdwarf-White Dwarf Super-Chandrasekhar Candidate
A hot subdwarf–white dwarf super-Chandrasekhar candidate supernova Ia progenitor Ingrid Pelisoli1,2*, P. Neunteufel3, S. Geier1, T. Kupfer4,5, U. Heber6, A. Irrgang6, D. Schneider6, A. Bastian1, J. van Roestel7, V. Schaffenroth1, and B. N. Barlow8 1Institut fur¨ Physik und Astronomie, Universitat¨ Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam-Golm, Germany 2Department of Physics, University of Warwick, Coventry, CV4 7AL, UK 3Max Planck Institut fur¨ Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei Munchen¨ 4Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA 5Texas Tech University, Department of Physics & Astronomy, Box 41051, 79409, Lubbock, TX, USA 6Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nuremberg (FAU), Sternwartstr. 7, 96049 Bamberg, Germany 7Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 8Department of Physics and Astronomy, High Point University, High Point, NC 27268, USA *[email protected] ABSTRACT Supernova Ia are bright explosive events that can be used to estimate cosmological distances, allowing us to study the expansion of the Universe. They are understood to result from a thermonuclear detonation in a white dwarf that formed from the exhausted core of a star more massive than the Sun. However, the possible progenitor channels leading to an explosion are a long-standing debate, limiting the precision and accuracy of supernova Ia as distance indicators. Here we present HD 265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf — a stripped core-helium burning star. -

Electric Propulsion System Scaling for Asteroid Capture-And-Return Missions
Electric propulsion system scaling for asteroid capture-and-return missions Justin M. Little⇤ and Edgar Y. Choueiri† Electric Propulsion and Plasma Dynamics Laboratory, Princeton University, Princeton, NJ, 08544 The requirements for an electric propulsion system needed to maximize the return mass of asteroid capture-and-return (ACR) missions are investigated in detail. An analytical model is presented for the mission time and mass balance of an ACR mission based on the propellant requirements of each mission phase. Edelbaum’s approximation is used for the Earth-escape phase. The asteroid rendezvous and return phases of the mission are modeled as a low-thrust optimal control problem with a lunar assist. The numerical solution to this problem is used to derive scaling laws for the propellant requirements based on the maneuver time, asteroid orbit, and propulsion system parameters. Constraining the rendezvous and return phases by the synodic period of the target asteroid, a semi- empirical equation is obtained for the optimum specific impulse and power supply. It was found analytically that the optimum power supply is one such that the mass of the propulsion system and power supply are approximately equal to the total mass of propellant used during the entire mission. Finally, it is shown that ACR missions, in general, are optimized using propulsion systems capable of processing 100 kW – 1 MW of power with specific impulses in the range 5,000 – 10,000 s, and have the potential to return asteroids on the order of 103 104 tons. − Nomenclature -
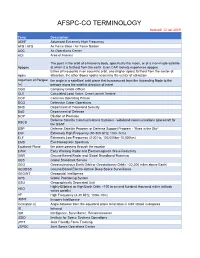
AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance -

Use of MESSENGER Radioscience Data to Improve Planetary Ephemeris and to Test General Relativity
A&A 561, A115 (2014) Astronomy DOI: 10.1051/0004-6361/201322124 & © ESO 2014 Astrophysics Use of MESSENGER radioscience data to improve planetary ephemeris and to test general relativity A. K. Verma1;2, A. Fienga3;4, J. Laskar4, H. Manche4, and M. Gastineau4 1 Observatoire de Besançon, UTINAM-CNRS UMR6213, 41bis avenue de l’Observatoire, 25000 Besançon, France e-mail: [email protected] 2 Centre National d’Études Spatiales, 18 avenue Édouard Belin, 31400 Toulouse, France 3 Observatoire de la Côte d’Azur, GéoAzur-CNRS UMR7329, 250 avenue Albert Einstein, 06560 Valbonne, France 4 Astronomie et Systèmes Dynamiques, IMCCE-CNRS UMR8028, 77 Av. Denfert-Rochereau, 75014 Paris, France Received 24 June 2013 / Accepted 7 November 2013 ABSTRACT The current knowledge of Mercury’s orbit has mainly been gained by direct radar ranging obtained from the 60s to 1998 and by five Mercury flybys made with Mariner 10 in the 70s, and with MESSENGER made in 2008 and 2009. On March 18, 2011, MESSENGER became the first spacecraft to orbit Mercury. The radioscience observations acquired during the orbital phase of MESSENGER drastically improved our knowledge of the orbit of Mercury. An accurate MESSENGER orbit is obtained by fitting one-and-half years of tracking data using GINS orbit determination software. The systematic error in the Earth-Mercury geometric positions, also called range bias, obtained from GINS are then used to fit the INPOP dynamical modeling of the planet motions. An improved ephemeris of the planets is then obtained, INPOP13a, and used to perform general relativity tests of the parametrized post-Newtonian (PPN) formalism. -

Orbit and Spin
Orbit and Spin Overview: A whole-body activity that explores the relative sizes, distances, orbit, and spin of the Sun, Earth, and Moon. Target Grade Level: 3-5 Estimated Duration: 2 40-minute sessions Learning Goals: Students will be able to… • compare the relative sizes of the Earth, Moon, and Sun. • contrast the distance between the Earth and Moon to the distance between the Earth and Sun. • differentiate between the motions of orbit and spin. • demonstrate the spins of the Earth and the Moon, as well as the orbits of the Earth around the Sun, and the Moon around the Earth. Standards Addressed: Benchmarks (AAAS, 1993) The Physical Setting, 4A: The Universe, 4B: The Earth National Science Education Standards (NRC, 1996) Physical Science, Standard B: Position and motion of objects Earth and Space Science, Standard D: Objects in the sky, Changes in Earth and sky Table of Contents: Background Page 1 Materials and Procedure 5 What I Learned… Science Journal Page 14 Earth Picture 15 Sun Picture 16 Moon Picture 17 Earth Spin Demonstration 18 Moon Orbit Demonstration 19 Extensions and Adaptations 21 Standards Addressed, detailed 22 Background: Sun The Sun is the center of our Solar System, both literally—as all of the planets orbit around it, and figuratively—as its rays warm our planet and sustain life as we know it. The Sun is very hot compared to temperatures we usually encounter. Its mean surface temperature is about 9980° Fahrenheit (5800 Kelvin) and its interior temperature is as high as about 28 million° F (15,500,000 Kelvin). -

Rideshare and the Orbital Maneuvering Vehicle: the Key to Low-Cost Lagrange-Point Missions
SSC15-II-5 Rideshare and the Orbital Maneuvering Vehicle: the Key to Low-cost Lagrange-point Missions Chris Pearson, Marissa Stender, Christopher Loghry, Joe Maly, Valentin Ivanitski Moog Integrated Systems 1113 Washington Avenue, Suite 300, Golden, CO, 80401; 303 216 9777, extension 204 [email protected] Mina Cappuccio, Darin Foreman, Ken Galal, David Mauro NASA Ames Research Center PO Box 1000, M/S 213-4, Moffett Field, CA 94035-1000; 650 604 1313 [email protected] Keats Wilkie, Paul Speth, Trevor Jackson, Will Scott NASA Langley Research Center 4 West Taylor Street, Mail Stop 230, Hampton, VA, 23681; 757 864 420 [email protected] ABSTRACT Rideshare is a well proven approach, in both LEO and GEO, enabling low-cost space access through splitting of launch charges between multiple passengers. Demand exists from users to operate payloads at Lagrange points, but a lack of regular rides results in a deficiency in rideshare opportunities. As a result, such mission architectures currently rely on a costly dedicated launch. NASA and Moog have jointly studied the technical feasibility, risk and cost of using an Orbital Maneuvering Vehicle (OMV) to offer Lagrange point rideshare opportunities. This OMV would be launched as a secondary passenger on a commercial rocket into Geostationary Transfer Orbit (GTO) and utilize the Moog ESPA secondary launch adapter. The OMV is effectively a free flying spacecraft comprising a full suite of avionics and a propulsion system capable of performing GTO to Lagrange point transfer via a weak stability boundary orbit. In addition to traditional OMV ’tug’ functionality, scenarios using the OMV to host payloads for operation at the Lagrange points have also been analyzed. -

Multi-Body Trajectory Design Strategies Based on Periapsis Poincaré Maps
MULTI-BODY TRAJECTORY DESIGN STRATEGIES BASED ON PERIAPSIS POINCARÉ MAPS A Dissertation Submitted to the Faculty of Purdue University by Diane Elizabeth Craig Davis In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy August 2011 Purdue University West Lafayette, Indiana ii To my husband and children iii ACKNOWLEDGMENTS I would like to thank my advisor, Professor Kathleen Howell, for her support and guidance. She has been an invaluable source of knowledge and ideas throughout my studies at Purdue, and I have truly enjoyed our collaborations. She is an inspiration to me. I appreciate the insight and support from my committee members, Professor James Longuski, Professor Martin Corless, and Professor Daniel DeLaurentis. I would like to thank the members of my research group, past and present, for their friendship and collaboration, including Geoff Wawrzyniak, Chris Patterson, Lindsay Millard, Dan Grebow, Marty Ozimek, Lucia Irrgang, Masaki Kakoi, Raoul Rausch, Matt Vavrina, Todd Brown, Amanda Haapala, Cody Short, Mar Vaquero, Tom Pavlak, Wayne Schlei, Aurelie Heritier, Amanda Knutson, and Jeff Stuart. I thank my parents, David and Jeanne Craig, for their encouragement and love throughout my academic career. They have cheered me on through many years of studies. I am grateful for the love and encouragement of my husband, Jonathan. His never-ending patience and friendship have been a constant source of support. Finally, I owe thanks to the organizations that have provided the funding opportunities that have supported me through my studies, including the Clare Booth Luce Foundation, Zonta International, and Purdue University and the School of Aeronautics and Astronautics through the Graduate Assistance in Areas of National Need and the Purdue Forever Fellowships. -

Analysis of Transfer Maneuvers from Initial
Revista Mexicana de Astronom´ıa y Astrof´ısica, 52, 283–295 (2016) ANALYSIS OF TRANSFER MANEUVERS FROM INITIAL CIRCULAR ORBIT TO A FINAL CIRCULAR OR ELLIPTIC ORBIT M. A. Sharaf1 and A. S. Saad2,3 Received March 14 2016; accepted May 16 2016 RESUMEN Presentamos un an´alisis de las maniobras de transferencia de una ´orbita circu- lar a una ´orbita final el´ıptica o circular. Desarrollamos este an´alisis para estudiar el problema de las transferencias impulsivas en las misiones espaciales. Consideramos maniobras planas usando ecuaciones reci´enobtenidas; con estas ecuaciones se com- paran las maniobras circulares y el´ıpticas. Esta comparaci´on es importante para el dise˜no´optimo de misiones espaciales, y permite obtener mapeos ´utiles para mostrar cu´al es la mejor maniobra. Al respecto, desarrollamos este tipo de comparaciones mediante 10 resultados, y los mostramos gr´aficamente. ABSTRACT In the present paper an analysis of the transfer maneuvers from initial circu- lar orbit to a final circular or elliptic orbit was developed to study the problem of impulsive transfers for space missions. It considers planar maneuvers using newly derived equations. With these equations, comparisons of circular and elliptic ma- neuvers are made. This comparison is important for the mission designers to obtain useful mappings showing where one maneuver is better than the other. In this as- pect, we developed this comparison throughout ten results, together with some graphs to show their meaning. Key Words: celestial mechanics — methods: analytical — space vehicles 1. INTRODUCTION The large amount of information from interplanetary missions, such as Pioneer (Dyer et al. -

Perturbation Theory in Celestial Mechanics
Perturbation Theory in Celestial Mechanics Alessandra Celletti Dipartimento di Matematica Universit`adi Roma Tor Vergata Via della Ricerca Scientifica 1, I-00133 Roma (Italy) ([email protected]) December 8, 2007 Contents 1 Glossary 2 2 Definition 2 3 Introduction 2 4 Classical perturbation theory 4 4.1 The classical theory . 4 4.2 The precession of the perihelion of Mercury . 6 4.2.1 Delaunay action–angle variables . 6 4.2.2 The restricted, planar, circular, three–body problem . 7 4.2.3 Expansion of the perturbing function . 7 4.2.4 Computation of the precession of the perihelion . 8 5 Resonant perturbation theory 9 5.1 The resonant theory . 9 5.2 Three–body resonance . 10 5.3 Degenerate perturbation theory . 11 5.4 The precession of the equinoxes . 12 6 Invariant tori 14 6.1 Invariant KAM surfaces . 14 6.2 Rotational tori for the spin–orbit problem . 15 6.3 Librational tori for the spin–orbit problem . 16 6.4 Rotational tori for the restricted three–body problem . 17 6.5 Planetary problem . 18 7 Periodic orbits 18 7.1 Construction of periodic orbits . 18 7.2 The libration in longitude of the Moon . 20 1 8 Future directions 20 9 Bibliography 21 9.1 Books and Reviews . 21 9.2 Primary Literature . 22 1 Glossary KAM theory: it provides the persistence of quasi–periodic motions under a small perturbation of an integrable system. KAM theory can be applied under quite general assumptions, i.e. a non– degeneracy of the integrable system and a diophantine condition of the frequency of motion.