DOCSLIB.ORG

Calculus on the Complex Plane C

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Calculus on the Complex Plane C Calculus on the complex plane C Let z = x + iy be the complex√ variable on the complex plane C == R × iR where i = −1. Definition A function f : C → C is holomorphic if it is complex differentiable, i.e., for each z ∈ C, f(z + h) − f(z) f0(z) = lim h→0 h exists. When f is non-constant, this is equivalent to the property: Except for isolated points, if c1, c2 are any two orthogonal curves passing through a point p ∈ C, then their image curves f ◦ c1, f ◦ c2 are orthogonal curves at f(p). This property is also equivalent to the property that the function f is angle preserving (conformal) except at isolated points, when it is not constant. Calculus on the complex plane C Definition A function f : M1 → M2 between two surfaces is called holomorphic if it is angle preserving except at isolated points, when 2 it is not constant. It is called meromorphic if M2 = S is the unit sphere in R3. A function f : R2 → R is called harmonic if f satisfies the mean value property, i.e., the value of f(p) at any point p ∈ R2, is equal to the average value of the function on every circle centered at p. Also f : R2 → R is harmonic if its Laplacian vanishes, ∆f = 0 Example If T is a temperature function in equilibrium on a domain D in the plane, then T is a harmonic function. Theorem A harmonic function f : M → R on a surface is the real part of some holomorphic function F : M → C = R × iR. Definition of minimal surface A surface f : M → R3 is minimal if: M has MEAN CURVATURE = 0. Small pieces have LEAST AREA. Small pieces have LEAST ENERGY. Small pieces occur as SOAP FILMS. Coordinate functions are HARMONIC. Conformal Gauss map G: M → S2 = C ∪ {∞}. MEROMORPHIC GAUSS MAP Meromorphic Gauss map Weierstrass Representation Suppose f : M ⊂ R3 is minimal, g: M → C ∪ {∞}, is the meromorphic Gauss map, dh = dx3 + i ∗ dx3, is the holomorphic height differential. Then Z p 1 1 i 1 f(p) = Re − g, + g , 1 dh. 2 g 2 g Helicoid Image by Matthias Weber M = C dh = dz = dx+i dy g(z) = eiz Catenoid Image by Matthias Weber M = C − {(0, 0)} 1 dh = dz z g(z) = z Catenoid. Image by Matthias Weber Key Properties: In 1741, Euler discovered that when a catenary x1 = cosh x3 is rotated around the x3-axis, then one obtains a surface which minimizes area among surfaces of revolution after prescribing boundary values for the generating curves. In 1776, Meusnier verified that the catenoid has zero mean curvature. This surface has genus zero, two ends and total curvature −4π. Catenoid. Image by Matthias Weber Key Properties: Together with the plane, the catenoid is the only minimal surface of revolution (Euler and Bonnet). It is the unique complete, embedded minimal surface with genus zero, finite topology and more than one end (L´opez and Ros). The catenoid is characterized as being the unique complete, embedded minimal surface with finite topology and two ends (Schoen). Helicoid. Image by Matthias Weber Key Properties: Proved to be minimal by Meusnier in 1776. The helicoid has genus zero, one end and infinite total curvature. Together with the plane, the helicoid is the only ruled minimal surface (Catalan). It is the unique simply-connected, complete, embedded minimal surface (Meeks and Rosenberg, Colding and Minicozzi). Enneper surface. Image by Matthias Weber Key Properties: Weierstrass Data: M = C, g(z) = z, dh = z dz. Discovered by Enneper in 1864, using his newly formulated analytic representation of minimal surfaces in terms of holomorphic data, equivalent to the Weierstrass representation. This surface is non-embedded, has genus zero, one end and total curvature −4π. It contains two horizontal orthogonal lines and the surface has two vertical planes of reflective symmetry. Meeks minimal M¨obius strip. Image by Matthias Weber Key Properties: 2 z+1 Weierstrass Data: M = C − {0}, g(z) = z z−1 , z2−1 dh = i z2 dz. Found by Meeks, the minimal surface defined by this Weierstrass 3 pair double covers a complete, immersed minimal surface M1 ⊂ R which is topologically a M¨obius strip. This is the unique complete, minimally immersed surface in R3 of finite total curvature −6π (Meeks). Bent helicoids. Image by Matthias Weber Key Properties: zn+i zn+z−n Weierstrass Data: M = C − {0}, g(z) = −z izn+i , dh = 2z dz. Discovered in 2004 by Meeks and Weber and independently by Mira. Costa torus. Image by Matthias Weber Key Properties: Weierstrass Data: Based on the square torus 2 1 1 M = C/Z − {(0, 0), ( 2 , 0), (0, 2 )}, g(z) = P(z). Discovered in 1982 by Costa. This is a thrice punctured torus with total curvature −12π, two catenoidal ends and one planar middle end. Hoffman and Meeks proved its global embeddedness. The Costa surface contains two horizontal straight lines l1, l2 that intersect orthogonally, and has vertical planes of symmetry bisecting the right angles made by l1, l2. Costa-Hoffman-Meeks surfaces. Image by M. Weber Key Properties: 2 Weierstrass Data: Defined in terms of cyclic covers of S . These examples Mk generalize the Costa torus, and are complete, embedded, genus k minimal surfaces with two catenoidal ends and one planar middle end. Both existence and embeddedness were given by Hoffman and Meeks in 1990. Deformation of the Costa torus. Image by M. Weber Key Properties: The Costa surface is defined on a square torus M1,1, and admits a deformation (found by Hoffman and Meeks, unpublished) where the planar end becomes catenoidal. Genus-one helicoid. Key Properties: The unique end of M is asymptotic to a helicoid, so that one of the two lines contained in the surface is an axis (like in the genuine helicoid). Discovered in 1993 by Hoffman, Karcher and Wei. Proved embedded in 2007 by Hoffman, Weber and Wolf. Singly-periodic Scherk surfaces. Image by M. Weber Key Properties: Weierstrass Data: M = (C ∪ {∞}) − {±e±iθ/2}, g(z) = z, dh = iz dz , for fixed θ ∈ (0, π/2]. Q(z±e±iθ/2) Discovered by Scherk in 1835, these surfaces denoted by Sθ form a 1-parameter family of complete, embedded, genus zero minimal surfaces in a quotient of R3 by a translation, and have four annular ends. 3 Viewed in R , each surface Sθ is invariant under reflection in the (x1, x3) and (x2, x3)-planes and in horizontal planes at integer heights, and can be thought of geometrically as a desingularization of two vertical planes forming an angle of θ. Doubly-periodic Scherk surfaces. Image by M. Weber Key Properties: Weierstrass Data: M = (C ∪ {∞}) − {±e±iθ/2}, g(z) = z, dh = z dz , where θ ∈ (0, π/2] (the case θ = π . Q(z±e±iθ/2) 2 It has implicit equation ez cos y = cos x. Discovered by Scherk in 1835, are the conjugate surfaces to the singly-periodic Scherk surfaces. Schwarz Primitive triply-periodic surface. Image by Weber Key Properties: Weierstrass Data: M = {(z, w) ∈ (C ∪ {∞})2 | w 2 = z 8 − 14z 4 + 1}, z dz g(z, w) = z, dh = w . Discovered by Schwarz in the 1880’s, it is also called the P-surface. This surface has a rank three symmetry group and is invariant by 3 translations in Z . Such a structure, common to any triply-periodic minimal surface (TPMS), is also known as a crystallographic cell or space tiling. Embedded TPMS divide R3 into two connected components (called labyrinths in crystallography), sharing M as boundary (or interface) and interweaving each other. Schwarz Diamond surfaces. Image by M. Weber Discovered by Schwarz, it is the conjugate surface to the P-surface, and is another famous example of an embedded TPMS. Schoen’s triply-periodic Gyroid surface. Image by Weber In the 1960’s, Schoen made a surprising discovery: another minimal surface locally isometric to the Primitive and Diamond surface is an embedded TPMS, and named this surface the Gyroid. 1860 Riemann’s discovery! Image by Matthias Weber Figure: Riemann minimal examples. Image by Matthias Weber Key Properties: Discovered in 1860 by Riemann, these examples are invariant under reflection in the (x1, x3)-plane and by a translation Tλ. After appropriate scalings, they converge to catenoids as t → 0 or to helicoids as t → ∞. The Riemann minimal examples have the amazing property that every horizontal plane intersects the surface in a circle or in a line. Meeks, P´erez and Ros proved these surfaces are the only properly embedded minimal surfaces in R3 of genus 0 and infinite topology. Introduction and history of the problem Problem: Classify all PEMS in R3 with genus zero. k = #{ends} L´opez-Ros, 1991: Finite total curvature ⇒ plane, catenoid Introduction and history of the problem Problem: Classify all PEMS in R3 with genus zero. k = #{ends} L´opez-Ros, 1991: Finite total curvature ⇒ plane, catenoid Introduction and history of the problem Problem: Classify all PEMS in R3 with genus zero. k = #{ends} L´opez-Ros, 1991: Finite total curvature ⇒ plane, catenoid Introduction and history of the problem Problem: Classify all PEMS in R3 with genus zero. k = #{ends} L´opez-Ros, 1991: Finite total curvature ⇒ plane, catenoid Collin, 1997: Finite topology and k > 1 ⇒ finite total curvature. Introduction and history of the problem Problem: Classify all PEMS in R3 with genus zero. k = #{ends} L´opez-Ros, 1991: Finite total curvature ⇒ plane, catenoid Collin, 1997: Finite topology and k > 1 ⇒ finite total curvature. Colding-Minicozzi, 2004: limits of simply connected minimal sur- faces = minimal laminations.
Load more

Recommended publications
  • Integration in the Complex Plane (Zill & Wright Chapter
    Integration in the Complex Plane (Zill & Wright Chapter 18) 1016-420-02: Complex Variables∗ Winter 2012-2013 Contents 1 Contour Integrals 2 1.1 Definition and Properties . 2 1.2 Evaluation . 3 1.2.1 Example: R z¯ dz ............................. 3 C1 1.2.2 Example: R z¯ dz ............................. 4 C2 R 2 1.2.3 Example: C z dz ............................. 4 1.3 The ML Limit . 5 1.4 Circulation and Flux . 5 2 The Cauchy-Goursat Theorem 7 2.1 Integral Around a Closed Loop . 7 2.2 Independence of Path for Analytic Functions . 8 2.3 Deformation of Closed Contours . 9 2.4 The Antiderivative . 10 3 Cauchy's Integral Formulas 12 3.1 Cauchy's Integral Formula . 12 3.1.1 Example #1 . 13 3.1.2 Example #2 . 13 3.2 Cauchy's Integral Formula for Derivatives . 14 3.3 Consequences of Cauchy's Integral Formulas . 16 3.3.1 Cauchy's Inequality . 16 3.3.2 Liouville's Theorem . 16 ∗Copyright 2013, John T. Whelan, and all that 1 Tuesday 18 December 2012 1 Contour Integrals 1.1 Definition and Properties Recall the definition of the definite integral Z xF X f(x) dx = lim f(xk) ∆xk (1.1) ∆xk!0 xI k We'd like to define a similar concept, integrating a function f(z) from some point zI to another point zF . The problem is that, since zI and zF are points in the complex plane, there are different ways to get between them, and adding up the value of the function along one path will not give the same result as doing it along another path, even if they have the same endpoints.
    [Show full text]
  • Brief Information on the Surfaces Not Included in the Basic Content of the Encyclopedia
    Brief Information on the Surfaces Not Included in the Basic Content of the Encyclopedia Brief information on some classes of the surfaces which cylinders, cones and ortoid ruled surfaces with a constant were not picked out into the special section in the encyclo- distribution parameter possess this property. Other properties pedia is presented at the part “Surfaces”, where rather known of these surfaces are considered as well. groups of the surfaces are given. It is known, that the Plücker conoid carries two-para- At this section, the less known surfaces are noted. For metrical family of ellipses. The straight lines, perpendicular some reason or other, the authors could not look through to the planes of these ellipses and passing through their some primary sources and that is why these surfaces were centers, form the right congruence which is an algebraic not included in the basic contents of the encyclopedia. In the congruence of the4th order of the 2nd class. This congru- basis contents of the book, the authors did not include the ence attracted attention of D. Palman [8] who studied its surfaces that are very interesting with mathematical point of properties. Taking into account, that on the Plücker conoid, view but having pure cognitive interest and imagined with ∞2 of conic cross-sections are disposed, O. Bottema [9] difficultly in real engineering and architectural structures. examined the congruence of the normals to the planes of Non-orientable surfaces may be represented as kinematics these conic cross-sections passed through their centers and surfaces with ruled or curvilinear generatrixes and may be prescribed a number of the properties of a congruence of given on a picture.
    [Show full text]
  • 1 the Complex Plane
    Math 135A, Winter 2012 Complex numbers 1 The complex numbers C are important in just about every branch of mathematics. These notes present some basic facts about them. 1 The Complex Plane A complex number z is given by a pair of real numbers x and y and is written in the form z = x+iy, where i satisfies i2 = −1. The complex numbers may be represented as points in the plane, with the real number 1 represented by the point (1; 0), and the complex number i represented by the point (0; 1). The x-axis is called the \real axis," and the y-axis is called the \imaginary axis." For example, the complex numbers 1, i, 3 + 4i and 3 − 4i are illustrated in Fig 1a. 3 + 4i 6 + 4i 2 + 3i imag i 4 + i 1 real 3 − 4i Fig 1a Fig 1b Complex numbers are added in a natural way: If z1 = x1 + iy1 and z2 = x2 + iy2, then z1 + z2 = (x1 + x2) + i(y1 + y2) (1) It's just vector addition. Fig 1b illustrates the addition (4 + i) + (2 + 3i) = (6 + 4i). Multiplication is given by z1z2 = (x1x2 − y1y2) + i(x1y2 + x2y1) Note that the product behaves exactly like the product of any two algebraic expressions, keeping in mind that i2 = −1. Thus, (2 + i)(−2 + 4i) = 2(−2) + 8i − 2i + 4i2 = −8 + 6i We call x the real part of z and y the imaginary part, and we write x = Re z, y = Im z.(Remember: Im z is a real number.) The term \imaginary" is a historical holdover; it took mathematicians some time to accept the fact that i (for \imaginary," naturally) was a perfectly good mathematical object.
    [Show full text]
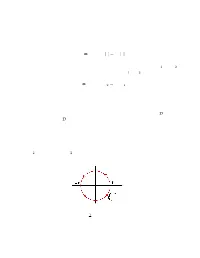
  • The Integral Resulting in a Logarithm of a Complex Number Dr. E. Jacobs in first Year Calculus You Learned About the Formula: Z B 1 Dx = Ln |B| − Ln |A| a X
    The Integral Resulting in a Logarithm of a Complex Number Dr. E. Jacobs In first year calculus you learned about the formula: Z b 1 dx = ln jbj ¡ ln jaj a x It is natural to want to apply this formula to contour integrals. If z1 and z2 are complex numbers and C is a path connecting z1 to z2, we would expect that: Z 1 dz = log z2 ¡ log z1 C z However, you are about to see that there is an interesting complication when we take the formula for the integral resulting in logarithm and try to extend it to the complex case. First of all, recall that if f(z) is an analytic function on a domain D and C is a closed loop in D then : I f(z) dz = 0 This is referred to as the Cauchy-Integral Theorem. So, for example, if C His a circle of radius r around the origin we may conclude immediately that 2 2 C z dz = 0 because z is an analytic function for all values of z. H If f(z) is not analytic then C f(z) dz is not necessarily zero. Let’s do an 1 explicit calculation for f(z) = z . If we are integrating around a circle C centered at the origin, then any point z on this path may be written as: z = reiθ H 1 iθ Let’s use this to integrate C z dz. If z = re then dz = ireiθ dθ H 1 Now, substitute this into the integral C z dz.
    [Show full text]
  • Scalable Synthesis of Gyroid-Inspired Freestanding Three-Dimensional Graphene Architectures† Cite This: DOI: 10.1039/C9na00358d Adrian E
    Nanoscale Advances View Article Online COMMUNICATION View Journal Scalable synthesis of gyroid-inspired freestanding three-dimensional graphene architectures† Cite this: DOI: 10.1039/c9na00358d Adrian E. Garcia,a Chen Santillan Wang, a Robert N. Sanderson,b Kyle M. McDevitt,a c ac a d Received 5th June 2019 Yunfei Zhang, Lorenzo Valdevit, Daniel R. Mumm, Ali Mohraz a Accepted 16th September 2019 and Regina Ragan * DOI: 10.1039/c9na00358d rsc.li/nanoscale-advances Three-dimensional porous architectures of graphene are desirable for Introduction energy storage, catalysis, and sensing applications. Yet it has proven challenging to devise scalable methods capable of producing co- Porous 3D architectures composed of graphene lms can continuous architectures and well-defined, uniform pore and liga- improve performance of carbon-based scaffolds in applications Creative Commons Attribution-NonCommercial 3.0 Unported Licence. ment sizes at length scales relevant to applications. This is further such as electrochemical energy storage,1–4 catalysis,5 sensing,6 complicated by processing temperatures necessary for high quality and tissue engineering.7,8 Graphene's remarkably high elec- graphene. Here, bicontinuous interfacially jammed emulsion gels trical9 and thermal conductivities,10 mechanical strength,11–13 (bijels) are formed and processed into sacrificial porous Ni scaffolds for large specic surface area,14 and chemical stability15 have led to chemical vapor deposition to produce freestanding three-dimensional numerous explorations of this multifunctional material due to turbostratic graphene (bi-3DG) monoliths with high specificsurface its promise to impact multiple elds. While these specic area. Scanning electron microscopy (SEM) images show that the bi- applications typically require porous 3D architectures, gra- 3DG monoliths inherit the unique microstructural characteristics of phene growth has been most heavily investigated on 2D their bijel parents.
    [Show full text]
  • Complex Sinusoids Copyright C Barry Van Veen 2014
    Complex Sinusoids Copyright c Barry Van Veen 2014 Feel free to pass this ebook around the web... but please do not modify any of its contents. Thanks! AllSignalProcessing.com Key Concepts 1) The real part of a complex sinusoid is a cosine wave and the imag- inary part is a sine wave. 2) A complex sinusoid x(t) = AejΩt+φ can be visualized in the complex plane as a vector of length A that is rotating at a rate of Ω radians per second and has angle φ relative to the real axis at time t = 0. a) The projection of the complex sinusoid onto the real axis is the cosine A cos(Ωt + φ). b) The projection of the complex sinusoid onto the imaginary axis is the cosine A sin(Ωt + φ). AllSignalProcessing.com 3) The output of a linear time invariant system in response to a com- plex sinusoid input is a complex sinusoid of the of the same fre- quency. The system only changes the amplitude and phase of the input complex sinusoid. a) Arbitrary input signals are represented as weighted sums of complex sinusoids of different frequencies. b) Then, the output is a weighted sum of complex sinusoids where the weights have been multiplied by the complex gain of the system. 4) Complex sinusoids also simplify algebraic manipulations. AllSignalProcessing.com 5) Real sinusoids can be expressed as a sum of a positive and negative frequency complex sinusoid. 6) The concept of negative frequency is not physically meaningful for real data and is an artifact of using complex sinusoids.
    [Show full text]
  • Optical Properties of Gyroid Structured Materials: from Photonic Crystals to Metamaterials
    REVIEW ARTICLE Optical properties of gyroid structured materials: from photonic crystals to metamaterials James A. Dolan1;2;3, Bodo D. Wilts2;4, Silvia Vignolini5, Jeremy J. Baumberg3, Ullrich Steiner2;4 and Timothy D. Wilkinson1 1 Department of Engineering, University of Cambridge, JJ Thomson Avenue, CB3 0FA, Cambridge, United Kingdom 2 Cavendish Laboratory, Department of Physics, University of Cambridge, JJ Thomson Avenue, CB3 0HE, Cambridge, United Kingdom 3 NanoPhotonics Centre, Cavendish Laboratory, Department of Physics, University of Cambridge, JJ Thomson Avenue, CB3 0HE, Cambridge, United Kingdom 4 Adolphe Merkle Institute, University of Fribourg, Chemin des Verdiers 4, CH-1700 Fribourg, Switzerland 5 Department of Chemistry, University of Cambridge, Lensfield Road, CB2 1EW, Cambridge, United Kingdom E-mail: [email protected]; [email protected]; [email protected]; [email protected]; [email protected]; [email protected] Abstract. The gyroid is a continuous and triply periodic cubic morphology which possesses a constant mean curvature surface across a range of volumetric fill fractions. Found in a variety of natural and synthetic systems which form through self-assembly, from butterfly wing scales to block copolymers, the gyroid also exhibits an inherent chirality not observed in any other similar morphologies. These unique geometrical properties impart to gyroid structured materials a host of interesting optical properties. Depending on the length scale on which the constituent materials are organised, these properties arise from starkly different physical mechanisms (such as a complete photonic band gap for photonic crystals and a greatly depressed plasma frequency for optical metamaterials). This article reviews the theoretical predictions and experimental observations of the optical properties of two fundamental classes of gyroid structured materials: photonic crystals (wavelength scale) and metamaterials (sub- wavelength scale).
    [Show full text]
  • Quintic Parametric Polynomial Minimal Surfaces and Their Properties
    Differential Geometry and its Applications 28 (2010) 697–704 Contents lists available at ScienceDirect Differential Geometry and its Applications www.elsevier.com/locate/difgeo Quintic parametric polynomial minimal surfaces and their properties ∗ Gang Xu a,c, ,Guo-zhaoWangb a Hangzhou Dianzi University, Hangzhou 310018, PR China b Department of Mathematics, Zhejiang University, Hangzhou 310027, PR China c Galaad, INRIA Sophia-Antipolis, 2004 Route des Lucioles, 06902 Sophia-Antipolis Cedex, France article info abstract Article history: In this paper, quintic parametric polynomial minimal surface and their properties are Received 28 November 2009 discussed. We first propose the sufficient condition of quintic harmonic polynomial Received in revised form 14 April 2010 parametric surface being a minimal surface. Then several new models of minimal surfaces Available online 31 July 2010 with shape parameters are derived from this condition. We also study the properties Communicated by Z. Shen of new minimal surfaces, such as symmetry, self-intersection on symmetric planes and MSC: containing straight lines. Two one-parameter families of isometric minimal surfaces are 53A10 also constructed by specifying some proper shape parameters. 49Q05 © 2010 Elsevier B.V. All rights reserved. 49Q10 Keywords: Minimal surface Harmonic surfaces Isothermal parametric surface Isometric minimal surfaces 1. Introduction Since Lagrange derived the minimal surface equation in R3 in 1762, minimal surfaces have a long history of over 200 years. A minimal surface is a surface with vanishing mean curvature. As the mean curvature is the variation of area functional, minimal surfaces include the surfaces minimizing the area with a fixed boundary. Because of their attractive properties, minimal surfaces have been extensively employed in many areas such as architecture, material science, aviation, ship manufacture, biology and so on.
    [Show full text]
  • Complex Analysis
    Complex Analysis Andrew Kobin Fall 2010 Contents Contents Contents 0 Introduction 1 1 The Complex Plane 2 1.1 A Formal View of Complex Numbers . .2 1.2 Properties of Complex Numbers . .4 1.3 Subsets of the Complex Plane . .5 2 Complex-Valued Functions 7 2.1 Functions and Limits . .7 2.2 Infinite Series . 10 2.3 Exponential and Logarithmic Functions . 11 2.4 Trigonometric Functions . 14 3 Calculus in the Complex Plane 16 3.1 Line Integrals . 16 3.2 Differentiability . 19 3.3 Power Series . 23 3.4 Cauchy's Theorem . 25 3.5 Cauchy's Integral Formula . 27 3.6 Analytic Functions . 30 3.7 Harmonic Functions . 33 3.8 The Maximum Principle . 36 4 Meromorphic Functions and Singularities 37 4.1 Laurent Series . 37 4.2 Isolated Singularities . 40 4.3 The Residue Theorem . 42 4.4 Some Fourier Analysis . 45 4.5 The Argument Principle . 46 5 Complex Mappings 47 5.1 M¨obiusTransformations . 47 5.2 Conformal Mappings . 47 5.3 The Riemann Mapping Theorem . 47 6 Riemann Surfaces 48 6.1 Holomorphic and Meromorphic Maps . 48 6.2 Covering Spaces . 52 7 Elliptic Functions 55 7.1 Elliptic Functions . 55 7.2 Elliptic Curves . 61 7.3 The Classical Jacobian . 67 7.4 Jacobians of Higher Genus Curves . 72 i 0 Introduction 0 Introduction These notes come from a semester course on complex analysis taught by Dr. Richard Carmichael at Wake Forest University during the fall of 2010. The main topics covered include Complex numbers and their properties Complex-valued functions Line integrals Derivatives and power series Cauchy's Integral Formula Singularities and the Residue Theorem The primary reference for the course and throughout these notes is Fisher's Complex Vari- ables, 2nd edition.
    [Show full text]
  • Minimal Surfaces Saint Michael’S College
    MINIMAL SURFACES SAINT MICHAEL’S COLLEGE Maria Leuci Eric Parziale Mike Thompson Overview What is a minimal surface? Surface Area & Curvature History Mathematics Examples & Applications http://www.bugman123.com/MinimalSurfaces/Chen-Gackstatter-large.jpg What is a Minimal Surface? A surface with mean curvature of zero at all points Bounded VS Infinite A plane is the most trivial minimal http://commons.wikimedia.org/wiki/File:Costa's_Minimal_Surface.png surface Minimal Surface Area Cube side length 2 Volume enclosed= 8 Surface Area = 24 Sphere Volume enclosed = 8 r=1.24 Surface Area = 19.32 http://1.bp.blogspot.com/- fHajrxa3gE4/TdFRVtNB5XI/AAAAAAAAAAo/AAdIrxWhG7Y/s160 0/sphere+copy.jpg Curvature ~ rate of change More Curvature dT κ = ds Less Curvature History Joseph-Louis Lagrange first brought forward the idea in 1768 Monge (1776) discovered mean curvature must equal zero Leonhard Euler in 1774 and Jean Baptiste Meusiner in 1776 used Lagrange’s equation to find the first non- trivial minimal surface, the catenoid Jean Baptiste Meusiner in 1776 discovered the helicoid Later surfaces were discovered by mathematicians in the mid nineteenth century Soap Bubbles and Minimal Surfaces Principle of Least Energy A minimal surface is formed between the two boundaries. The sphere is not a minimal surface. http://arxiv.org/pdf/0711.3256.pdf Principal Curvatures Measures the amount that surfaces bend at a certain point Principal curvatures give the direction of the plane with the maximal and minimal curvatures http://upload.wikimedia.org/wi
    [Show full text]
  • On Bounds of the Sine and Cosine Along Straight Lines on the Complex Plane
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 19 September 2018 doi:10.20944/preprints201809.0365.v1 Peer-reviewed version available at Acta Universitatis Sapientiae, Mathematica 2019, 11, 371-379; doi:10.2478/ausm-2019-0027 ON BOUNDS OF THE SINE AND COSINE ALONG STRAIGHT LINES ON THE COMPLEX PLANE FENG QI Institute of Mathematics, Henan Polytechnic University, Jiaozuo, Henan, 454010, China College of Mathematics, Inner Mongolia University for Nationalities, Tongliao, Inner Mongolia, 028043, China Department of Mathematics, College of Science, Tianjin Polytechnic University, Tianjin, 300387, China E-mail: [email protected], [email protected] URL: https: // qifeng618. wordpress. com Abstract. In the paper, the author discusses and computes bounds of the sine and cosine along straight lines on the complex plane. 1. Motivations In the theory of complex functions, the sine and cosine on the complex plane C are denoted and defined by eiz − e−iz e−iz + e−iz sin z = and cos z = ; 2i 2 where z = x + iy and x; y 2 R. When z = x 2 R, these two functions become sin x and cos x which satisfy the periodicity and boundedness sin(x + 2kπ) = sin x; cos(x + 2kπ) = cos x; j sin xj ≤ 1; j cos xj ≤ 1 for k 2 Z. On the other hand, when z = iy for y 2 R, e−y − ey e−y + ey sin(iy) = ! ±i1 and cos(iy) = ! +1 2i 2 as y ! ±∞. These imply that the sine and cosine are bounded on the real x-axis, but unbounded on the imaginary y-axis. Motivated by the above boundedness, we naturally guess that the complex func- tions sin z and cos z for z 2 C are (1) bounded on all straight lines parallel to the real x-axis, (2) unbounded on all straight lines whose slopes are not horizontal.
    [Show full text]
  • Bour's Theorem in 4-Dimensional Euclidean
    Bull. Korean Math. Soc. 54 (2017), No. 6, pp. 2081{2089 https://doi.org/10.4134/BKMS.b160766 pISSN: 1015-8634 / eISSN: 2234-3016 BOUR'S THEOREM IN 4-DIMENSIONAL EUCLIDEAN SPACE Doan The Hieu and Nguyen Ngoc Thang Abstract. In this paper we generalize 3-dimensional Bour's Theorem 4 to the case of 4-dimension. We proved that a helicoidal surface in R 4 is isometric to a family of surfaces of revolution in R in such a way that helices on the helicoidal surface correspond to parallel circles on the surfaces of revolution. Moreover, if the surfaces are required further to have the same Gauss map, then they are hyperplanar and minimal. Parametrizations for such minimal surfaces are given explicitly. 1. Introduction Consider the deformation determined by a family of parametric surfaces given by Xθ(u; v) = (xθ(u; v); yθ(u; v); zθ(u; v)); xθ(u; v) = cos θ sinh v sin u + sin θ cosh v cos u; yθ(u; v) = − cos θ sinh v cos u + sin θ cosh v sin u; zθ(u; v) = u cos θ + v sin θ; where −π < u ≤ π; −∞ < v < 1 and the deformation parameter −π < θ ≤ π: A direct computation shows that all surfaces Xθ are minimal, have the same first fundamental form and normal vector field. We can see that X0 is the helicoid and Xπ=2 is the catenoid. Thus, locally the helicoid and catenoid are isometric and have the same Gauss map. Moreover, helices on the helicoid correspond to parallel circles on the catenoid.
    [Show full text]