DOCSLIB.ORG

Tetration and the Lambert Function

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Tetration and the Lambert Function TETRATION AND THE LAMBERT FUNCTION If one looks at the iteration- N[n 1] a N [n] subject to N[0] a one finds- a aa N[1] a a , N[2] a a and N[3] a a Whether or not this continued exponentiation of an exponentiation converges or not depends very much on the form of ‘a’. If a=2 we get N[0]=2, N[1]=22=4, N[2]=24=16, N[3]=216=65536. So things clearly blow up as the iteration continues toward n equal to infinity. On the other hand if a=1/2, we get N[1]=1/sqrt(2) , N[2]=(1/2)1/sqrt(2) and N[ ]=0.64118575.. Thus the iteration converges. Note that ‘a’ need not necessarily be real but rather can take on the complex value z=x+iy. The above iteration is commonly referred to as tetration indicating the fourth mathematical operation after addition , multiplication, and exponentiation. There are several different representations for tetration. These are- N N N N 4 N N 4 The arrows are perhaps the clearest notation indicating in this case that there are a total of four appearances of N. Sometimes the stacking of the Ns is also referred to as a power tower. Remember that the iteration process defined above differs from a multiplicative operation such as- (2^2^2)^2 (4^2)^2 (16)^2 256 Tetration is not associative with this last operation since it reads- 2^(2^(2^2))=2^(2^4)=2^16=65536 and typically has values much larger than the former. The fact that the numbers get very large rapidly with tetration makes this form of number representation ideal for very large numbers. Many of you will be familiar with the googol (after which the familiar search engine Google is named). One defines a googol as – 10 1 googol 1010 10100 and the even larger number, the googolplex, as- 1010 1 googolplex= 1010 10google Although such numbers are huge they still are in the sense of the WWI soldiers ditty, a long long way to infinity. To reach infinity you need – 10 Let us next turn our attention to all those numbers for which the iteration given above converges. For the purpose of generalization we will set - N=z=x+iy and a=A+iB This yields- x[n 1] iy[n 1] (A iB) x[n]iy[n] subject to z[0] A iB and so has both real and imaginary parts. The first two iterations yield- ( AiB ) z[1] (A iB)( AiB) and z[2] (A iB)( AiB) From this we see at once that the nth iteration is simply- z[n] (A iB) (n 1) Since we are only interested in those numbers z and a for which the iteration converges, we can quickly calculate this converengce point by noting z[n+1]=z[n] there. Thus we have the non-linear equation- z (A iB) z This equation lends itself to a particularly simple solution for the special case of A=0 and B=1. There we find- z exp(iz / 2) which, by Euler’s identity, is equivalent to- x exp(y / 2)cos(x / 2) and y exp(y / 2)sin(x / 2) These may be combined to yield the two implicit equations- x 2 y 2 exp(y) and tan(x / 2) y / x Solving these two equations numerically produces the result- x=0.438282936.. and y=0.36059247.. Thus the iteration convergers to- z=0.438282936 +i 0.36059247 in the complex plane. The precise trajectory to the convergence point is given by- z[n+1]=exp(iz[n]π/2) If we make a point plot of all these iterations starting with an initial condition z[0]=1 so that z[1]=i, we find the following interesting three branch inward moving spiral- The spiral is seen to move nicely to the convergence point. We first discovered this spiral some 15 years ago in our undergraduate complex variable course here at the University of Florida. It does not seem to matter where one starts the iteration as long as ‘a’ is set to i. The convergence point remains the same. Different spiral patterns will be created when the form of a=A+iB is changed. We have discussed such trajectories in an earlier article. Going back to the expression- z exp(iz / 2 one notes its resemblance to the Lambert function defined as- W (u) u exp(W (u)) So if we set iπz/2=-W(u), we get u=-iπ/2. Thus one finds – 2 i z W ( ) 0.43828293672703211162 i0.36059247187138548596 i 2 The Lambert function may also be used to determine the final convergence point for any other starting point – a=A+iB=R exp(i) We have the equation- z R z exp(iz ) exp{z(ln(R) i )} From this it follows that u=-(lnR+i) and- 1 z W ( ln(R) i ) ln(R) i If we now let a=1+i=sqrt(2)exp(iπ/4), we find the result- z 0.6410264785 + i0.5236284612I An iteration beginning with a=1/2 has A=1/2, B=0, R=1/2, and =0 . It produces the real convergence point- 1 z W (ln(2)) 0.64118574450498598451 ln(2) As a final evaluation consider a=sqrt(2) so that R=sqrt(2) and =0. Here we have- 2 2 2 2 2 2 W ((1/ 2) ln(2)) 2 ln(2) It produces the interesting identity- 1 ln(2) W (ln( )) 0.69314718055994530943… 2 April 2014 .
Load more

Recommended publications
  • The Enigmatic Number E: a History in Verse and Its Uses in the Mathematics Classroom
    To appear in MAA Loci: Convergence The Enigmatic Number e: A History in Verse and Its Uses in the Mathematics Classroom Sarah Glaz Department of Mathematics University of Connecticut Storrs, CT 06269 [email protected] Introduction In this article we present a history of e in verse—an annotated poem: The Enigmatic Number e . The annotation consists of hyperlinks leading to biographies of the mathematicians appearing in the poem, and to explanations of the mathematical notions and ideas presented in the poem. The intention is to celebrate the history of this venerable number in verse, and to put the mathematical ideas connected with it in historical and artistic context. The poem may also be used by educators in any mathematics course in which the number e appears, and those are as varied as e's multifaceted history. The sections following the poem provide suggestions and resources for the use of the poem as a pedagogical tool in a variety of mathematics courses. They also place these suggestions in the context of other efforts made by educators in this direction by briefly outlining the uses of historical mathematical poems for teaching mathematics at high-school and college level. Historical Background The number e is a newcomer to the mathematical pantheon of numbers denoted by letters: it made several indirect appearances in the 17 th and 18 th centuries, and acquired its letter designation only in 1731. Our history of e starts with John Napier (1550-1617) who defined logarithms through a process called dynamical analogy [1]. Napier aimed to simplify multiplication (and in the same time also simplify division and exponentiation), by finding a model which transforms multiplication into addition.
    [Show full text]
  • The Infinity Theorem Is Presented Stating That There Is at Least One Multivalued Series That Diverge to Infinity and Converge to Infinite Finite Values
    Open Journal of Mathematics and Physics | Volume 2, Article 75, 2020 | ISSN: 2674-5747 https://doi.org/10.31219/osf.io/9zm6b | published: 4 Feb 2020 | https://ojmp.wordpress.com CX [microresearch] Diamond Open Access The infinity theorem Open Mathematics Collaboration∗† March 19, 2020 Abstract The infinity theorem is presented stating that there is at least one multivalued series that diverge to infinity and converge to infinite finite values. keywords: multivalued series, infinity theorem, infinite Introduction 1. 1, 2, 3, ..., ∞ 2. N =x{ N 1, 2,∞3,}... ∞ > ∈ = { } The infinity theorem 3. Theorem: There exists at least one divergent series that diverge to infinity and converge to infinite finite values. ∗All authors with their affiliations appear at the end of this paper. †Corresponding author: [email protected] | Join the Open Mathematics Collaboration 1 Proof 1 4. S 1 1 1 1 1 1 ... 2 [1] = − + − + − + = (a) 5. Sn 1 1 1 ... 1 has n terms. 6. S = lim+n + S+n + 7. A+ft=er app→ly∞ing the limit in (6), we have S 1 1 1 ... + 8. From (4) and (7), S S 2 = 0 + 2 + 0 + 2 ... 1 + 9. S 2 2 1 1 1 .+.. = + + + + + + 1 10. Fro+m (=7) (and+ (9+), S+ )2 2S . + +1 11. Using (6) in (10), limn+ =Sn 2 2 limn Sn. 1 →∞ →∞ 12. limn Sn 2 + = →∞ 1 13. From (6) a=nd (12), S 2. + 1 14. From (7) and (13), S = 1 1 1 ... 2. + = + + + = (b) 15. S 1 1 1 1 1 ... + 1 16. S =0 +1 +1 +1 +1 +1 1 ..
    [Show full text]
  • The Modal Logic of Potential Infinity, with an Application to Free Choice
    The Modal Logic of Potential Infinity, With an Application to Free Choice Sequences Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Ethan Brauer, B.A. ∼6 6 Graduate Program in Philosophy The Ohio State University 2020 Dissertation Committee: Professor Stewart Shapiro, Co-adviser Professor Neil Tennant, Co-adviser Professor Chris Miller Professor Chris Pincock c Ethan Brauer, 2020 Abstract This dissertation is a study of potential infinity in mathematics and its contrast with actual infinity. Roughly, an actual infinity is a completed infinite totality. By contrast, a collection is potentially infinite when it is possible to expand it beyond any finite limit, despite not being a completed, actual infinite totality. The concept of potential infinity thus involves a notion of possibility. On this basis, recent progress has been made in giving an account of potential infinity using the resources of modal logic. Part I of this dissertation studies what the right modal logic is for reasoning about potential infinity. I begin Part I by rehearsing an argument|which is due to Linnebo and which I partially endorse|that the right modal logic is S4.2. Under this assumption, Linnebo has shown that a natural translation of non-modal first-order logic into modal first- order logic is sound and faithful. I argue that for the philosophical purposes at stake, the modal logic in question should be free and extend Linnebo's result to this setting. I then identify a limitation to the argument for S4.2 being the right modal logic for potential infinity.
    [Show full text]
  • Cantor on Infinity in Nature, Number, and the Divine Mind
    Cantor on Infinity in Nature, Number, and the Divine Mind Anne Newstead Abstract. The mathematician Georg Cantor strongly believed in the existence of actually infinite numbers and sets. Cantor’s “actualism” went against the Aristote- lian tradition in metaphysics and mathematics. Under the pressures to defend his theory, his metaphysics changed from Spinozistic monism to Leibnizian volunta- rist dualism. The factor motivating this change was two-fold: the desire to avoid antinomies associated with the notion of a universal collection and the desire to avoid the heresy of necessitarian pantheism. We document the changes in Can- tor’s thought with reference to his main philosophical-mathematical treatise, the Grundlagen (1883) as well as with reference to his article, “Über die verschiedenen Standpunkte in bezug auf das aktuelle Unendliche” (“Concerning Various Perspec- tives on the Actual Infinite”) (1885). I. he Philosophical Reception of Cantor’s Ideas. Georg Cantor’s dis- covery of transfinite numbers was revolutionary. Bertrand Russell Tdescribed it thus: The mathematical theory of infinity may almost be said to begin with Cantor. The infinitesimal Calculus, though it cannot wholly dispense with infinity, has as few dealings with it as possible, and contrives to hide it away before facing the world Cantor has abandoned this cowardly policy, and has brought the skeleton out of its cupboard. He has been emboldened on this course by denying that it is a skeleton. Indeed, like many other skeletons, it was wholly dependent on its cupboard, and vanished in the light of day.1 1Bertrand Russell, The Principles of Mathematics (London: Routledge, 1992 [1903]), 304.
    [Show full text]
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • Maths Secrets of Simpsons Revealed in New Book
    MONDAY 7 OCTOBER 2013 WWW.THEDAY.CO.UK Maths secrets of Simpsons revealed in new book The most successful TV show of all time is written by a team of brilliant ‘mathletes’, says writer Simon Singh, and full of obscure mathematical jokes. Can numbers really be all that funny? MATHEMATICS Nerd hero: The smartest girl in Springfield was created by a team of maths wizards. he world’s most popular cartoon a perfect number, a narcissistic number insist that their love of maths contrib- family has a secret: their lines are and a Mersenne Prime. utes directly to the more obvious humour written by a team of expert mathema- Another of these maths jokes – a black- that has made the show such a hit. Turn- Tticians – former ‘mathletes’ who are board showing 398712 + 436512 = 447212 ing intuitions about comedy into concrete as happy solving differential equa- – sent shivers down Simon Singh’s spine. jokes is like wrestling mathematical tions as crafting jokes. ‘I was so shocked,’ he writes, ‘I almost hunches into proofs and formulas. Comedy Now, science writer Simon Singh has snapped my slide rule.’ The numbers are and maths, says Cohen, are both explora- revealed The Simpsons’ secret math- a fake exception to a famous mathemati- tions into the unknown. ematical formula in a new book*. He cal rule known as Fermat’s Last Theorem. combed through hundreds of episodes One episode from 1990 features a Mathletes and trawled obscure internet forums to teacher making a maths joke to a class of Can maths really be funny? There are many discover that behind the show’s comic brilliant students in which Bart Simpson who will think comparing jokes to equa- exterior lies a hidden core of advanced has been accidentally included.
    [Show full text]
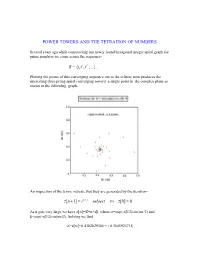
  • Power Towers and the Tetration of Numbers
    POWER TOWERS AND THE TETRATION OF NUMBERS Several years ago while constructing our newly found hexagonal integer spiral graph for prime numbers we came across the sequence- i S {i,i i ,i i ,...}, Plotting the points of this converging sequence out to the infinite term produces the interesting three prong spiral converging toward a single point in the complex plane as shown in the following graph- An inspection of the terms indicate that they are generated by the iteration- z[n 1] i z[n] subject to z[0] 0 As n gets very large we have z[]=Z=+i, where =exp(-/2)cos(/2) and =exp(-/2)sin(/2). Solving we find – Z=z[]=0.4382829366 + i 0.3605924718 It is the purpose of the present article to generalize the above result to any complex number z=a+ib by looking at the general iterative form- z[n+1]=(a+ib)z[n] subject to z[0]=1 Here N=a+ib with a and b being real numbers which are not necessarily integers. Such an iteration represents essentially a tetration of the number N. That is, its value up through the nth iteration, produces the power tower- Z Z n Z Z Z with n-1 zs in the exponents Thus- 22 4 2 22 216 65536 Note that the evaluation of the powers is from the top down and so is not equivalent to the bottom up operation 44=256. Also it is clear that the sequence {1 2,2 2,3 2,4 2,...}diverges very rapidly unlike the earlier case {1i,2 i,3i,4i,...} which clearly converges.
    [Show full text]
  • Measuring Fractals by Infinite and Infinitesimal Numbers
    MEASURING FRACTALS BY INFINITE AND INFINITESIMAL NUMBERS Yaroslav D. Sergeyev DEIS, University of Calabria, Via P. Bucci, Cubo 42-C, 87036 Rende (CS), Italy, N.I. Lobachevsky State University, Nizhni Novgorod, Russia, and Institute of High Performance Computing and Networking of the National Research Council of Italy http://wwwinfo.deis.unical.it/∼yaro e-mail: [email protected] Abstract. Traditional mathematical tools used for analysis of fractals allow one to distinguish results of self-similarity processes after a finite number of iterations. For example, the result of procedure of construction of Cantor’s set after two steps is different from that obtained after three steps. However, we are not able to make such a distinction at infinity. It is shown in this paper that infinite and infinitesimal numbers proposed recently allow one to measure results of fractal processes at different iterations at infinity too. First, the new technique is used to measure at infinity sets being results of Cantor’s proce- dure. Second, it is applied to calculate the lengths of polygonal geometric spirals at different points of infinity. 1. INTRODUCTION During last decades fractals have been intensively studied and applied in various fields (see, for instance, [4, 11, 5, 7, 12, 20]). However, their mathematical analysis (except, of course, a very well developed theory of fractal dimensions) very often continues to have mainly a qualitative character and there are no many tools for a quantitative analysis of their behavior after execution of infinitely many steps of a self-similarity process of construction. Usually, we can measure fractals in a way and can give certain numerical answers to questions regarding fractals only if a finite number of steps in the procedure of their construction has been executed.
    [Show full text]
  • A Child Thinking About Infinity
    A Child Thinking About Infinity David Tall Mathematics Education Research Centre University of Warwick COVENTRY CV4 7AL Young children’s thinking about infinity can be fascinating stories of extrapolation and imagination. To capture the development of an individual’s thinking requires being in the right place at the right time. When my youngest son Nic (then aged seven) spoke to me for the first time about infinity, I was fortunate to be able to tape-record the conversation for later reflection on what was happening. It proved to be a fascinating document in which he first treated infinity as a very large number and used his intuitions to think about various arithmetic operations on infinity. He also happened to know about “minus numbers” from earlier experiences with temperatures in centigrade. It was thus possible to ask him not only about arithmetic with infinity, but also about “minus infinity”. The responses were thought-provoking and amazing in their coherent relationships to his other knowledge. My research in studying infinite concepts in older students showed me that their ideas were influenced by their prior experiences. Almost always the notion of “limit” in some dynamic sense was met before the notion of one to one correspondences between infinite sets. Thus notions of “variable size” had become part of their intuition that clashed with the notion of infinite cardinals. For instance, Tall (1980) reported a student who considered that the limit of n2/n! was zero because the top is a “smaller infinity” than the bottom. It suddenly occurred to me that perhaps I could introduce Nic to the concept of cardinal infinity to see what this did to his intuitions.
    [Show full text]
  • The Exponential Function
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 5-2006 The Exponential Function Shawn A. Mousel University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Mousel, Shawn A., "The Exponential Function" (2006). MAT Exam Expository Papers. 26. https://digitalcommons.unl.edu/mathmidexppap/26 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. The Exponential Function Expository Paper Shawn A. Mousel In partial fulfillment of the requirements for the Masters of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor May 2006 Mousel – MAT Expository Paper - 1 One of the basic principles studied in mathematics is the observation of relationships between two connected quantities. A function is this connecting relationship, typically expressed in a formula that describes how one element from the domain is related to exactly one element located in the range (Lial & Miller, 1975). An exponential function is a function with the basic form f (x) = ax , where a (a fixed base that is a real, positive number) is greater than zero and not equal to 1. The exponential function is not to be confused with the polynomial functions, such as x 2. One way to recognize the difference between the two functions is by the name of the function.
    [Show full text]
  • Simple Statements, Large Numbers
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2007 Simple Statements, Large Numbers Shana Streeks University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Streeks, Shana, "Simple Statements, Large Numbers" (2007). MAT Exam Expository Papers. 41. https://digitalcommons.unl.edu/mathmidexppap/41 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Master of Arts in Teaching (MAT) Masters Exam Shana Streeks In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Gordon Woodward, Advisor July 2007 Simple Statements, Large Numbers Shana Streeks July 2007 Page 1 Streeks Simple Statements, Large Numbers Large numbers are numbers that are significantly larger than those ordinarily used in everyday life, as defined by Wikipedia (2007). Large numbers typically refer to large positive integers, or more generally, large positive real numbers, but may also be used in other contexts. Very large numbers often occur in fields such as mathematics, cosmology, and cryptography. Sometimes people refer to numbers as being “astronomically large”. However, it is easy to mathematically define numbers that are much larger than those even in astronomy. We are familiar with the large magnitudes, such as million or billion.
    [Show full text]
  • Attributes of Infinity
    International Journal of Applied Physics and Mathematics Attributes of Infinity Kiamran Radjabli* Utilicast, La Jolla, California, USA. * Corresponding author. Email: [email protected] Manuscript submitted May 15, 2016; accepted October 14, 2016. doi: 10.17706/ijapm.2017.7.1.42-48 Abstract: The concept of infinity is analyzed with an objective to establish different infinity levels. It is proposed to distinguish layers of infinity using the diverging functions and series, which transform finite numbers to infinite domain. Hyper-operations of iterated exponentiation establish major orders of infinity. It is proposed to characterize the infinity by three attributes: order, class, and analytic value. In the first order of infinity, the infinity class is assessed based on the “analytic convergence” of the Riemann zeta function. Arithmetic operations in infinity are introduced and the results of the operations are associated with the infinity attributes. Key words: Infinity, class, order, surreal numbers, divergence, zeta function, hyperpower function, tetration, pentation. 1. Introduction Traditionally, the abstract concept of infinity has been used to generically designate any extremely large result that cannot be measured or determined. However, modern mathematics attempts to introduce new concepts to address the properties of infinite numbers and operations with infinities. The system of hyperreal numbers [1], [2] is one of the approaches to define infinite and infinitesimal quantities. The hyperreals (a.k.a. nonstandard reals) *R, are an extension of the real numbers R that contains numbers greater than anything of the form 1 + 1 + … + 1, which is infinite number, and its reciprocal is infinitesimal. Also, the set theory expands the concept of infinity with introduction of various orders of infinity using ordinal numbers.
    [Show full text]