Popular Lectures and Addresses
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Horological TIMES June 1998
HoROLOGICAL TIMES June 1998 Horology on the Internet American Watchmakers-Clockmakers Institute Test, Analyze & Service Quartz Watches ~ ENG.NEERED & MANUFACTURED I THE U.S.A. ~ Accelerator The Accelerator is a high speed quartz watch gear train tester. It operates by induction power and allows the user to drive the gear train of a sealed watch with single steps or variable high speed control. The Accelerator will also determine if a sealed watch is operating electrically. FEATURES: Single step watch motor impulse control Set hands Variable watch motor impulse speed control Check battery without opening watch Variable watch motor intensity control Test electric circuit High-speed gear-train test Watch motor impulse indicator Release locked gear-trains High quality break resistant case Restart sealed watches Engineered & manufactured in the U.S.A. Improve gear lubrication #TS-2900 Cal-Pal Quartz Watch Analy:z:er------ The Cal-Pal is an intelligent countertop quartz watch analyzer engineered for the watch retail & service industries. FEATURES: Calibration of time accuracy in sec/24 hours Check battery without opening watch Battery tester for silver oxide, mercury, & lithium types Temperature compensating internal crystal oscillator Gear train evaluation via adjustable output voltage Solid state computer technology Current measurement in micro-amps Compact break resistant case (6"L x 3.5"W x 1.5"H) Coil resistance in Kilo-ohms Self test at turn on; Auto-off after 30 minutes of non-use Continuity tester via audio output High standard service center accuracy 16 Character alpha/numeric display Motor pulse audio & visual feedback Watch Mate-- -- Designed for the store where battery replacement is common. -

For People Who Love Maps Journal Advertising
161 INTERNATIONAL MAP COLLECTORS’ SOCIETY JUNE 2020 No. 161 Fine & Rare Antique Maps, Sea Charts, Town Views & Atlases R areMaps.com 7407 La Jolla Blvd. | La Jolla, CA 92037 [email protected] | 858.551.8500 FOR PEOPLE WHO LOVE MAPS JOURNAL ADVERTISING 4 issues per year Colour BW Index of Advertisers Full page (same copy) £1050 - Half page (same copy) £700 - Altea Gallery 64 Quarter page (same copy) £405 - Antiquariaat Sanderus 46 For a single issue Full page £425 - Barry Lawrence Ruderman outside back cover Half page £285 - Carta Historica 62 Quarter page £165 - Clive A. Burden Ltd 52 Advertisement formats for print Collecting Old Maps 17 We can accept advertisements as print ready CMYK 6 artwork saved as tiff, high quality jpegs or pdf files. Daniel Crouch Rare Books It is important to be aware that artwork and files Dominic Winter Auctioneers 29 that have been prepared for the web are not of sufficient quality for print. Full artwork specifications are available Doyle 45 on request. Forum Auctions 30 62 Advertisement sizes Frame Please note recommended image dimensions below: Jonathan Potter 4 Full page advertisements should be 216 mm high x 158 mm wide and 300–400 ppi at this size. Le Bail-Weissert 29 Half page advertisements are landscape and 105 mm Loeb-Larocque 47 high x 158 mm wide and 300–400 ppi at this size. Quarter page advertisements are portrait and are The Map House inside front cover 105 mm high x 76 mm wide and 300–400 ppi. Martayan Lan 2 IMCoS website Web banner Moleiro 50 Those who advertise in our Journal have priority in taking Mostly Maps 62 a web banner also. -

Encyclopaedia of Scientific Units, Weights and Measures Their SI Equivalences and Origins
FrancËois Cardarelli Encyclopaedia of Scientific Units, Weights and Measures Their SI Equivalences and Origins English translation by M.J. Shields, FIInfSc, MITI 13 Other Systems 3 of Units Despite the internationalization of SI units, and the fact that other units are actually forbidden by law in France and other countries, there are still some older or parallel systems remaining in use in several areas of science and technology. Before presenting conversion tables for them, it is important to put these systems into their initial context. A brief review of systems is given ranging from the ancient and obsolete (e.g. Egyptian, Greek, Roman, Old French) to the relatively modern and still in use (e.g. UK imperial, US customary, cgs, FPS), since a general knowledge of these systems can be useful in conversion calculations. Most of the ancient systems are now totally obsolete, and are included for general or historical interest. 3.1 MTS, MKpS, MKSA 3.1.1 The MKpS System The former system of units referred to by the international abbreviations MKpS, MKfS, or MKS (derived from the French titles meÁtre-kilogramme-poids-seconde or meÁtre-kilo- gramme-force-seconde) was in fact entitled SysteÁme des MeÂcaniciens (Mechanical Engi- neers' System). It was based on three fundamental units, the metre, the second, and a weight unit, the kilogram-force. This had the basic fault of being dependent on the acceleration due to gravity g, which varies on different parts of the Earth, so that the unit could not be given a general definition. Furthermore, because of the lack of a unit of mass, it was difficult, if not impossible to draw a distinction between weight, or force, and mass (see also 3.4). -

A Selection of New Arrivals December 2017
A selection of new arrivals December 2017 Rare and important books & manuscripts in science and medicine, by Christian Westergaard. Flæsketorvet 68 – 1711 København V – Denmark Cell: (+45)27628014 www.sophiararebooks.com AMPÈRE, André Marie. Mémoires ‘ONE OF THE MOST BRILLIANT ACHIEVEMENTS IN SCIENCE’ - JAMES CLERK MAXWELL AMPÈRE, André Marie. Mémoires sur l’action mutuelle de deux courans électriques, sur celle exise entre un courant électrique et un amiant ou le globe terrestre, et celle de deux aimans l’un sur l’autre. Paris: l’Academie royale des Sciences, [1820]. $16,500 8vo (197 x 127 mm), pp. 68 with five folding engraved plates. Plain blue wrappers. A very clean and fresh copy. First edition, very rare offprint issue, of Ampère’s “first great memoir on electrodynamics” (DSB). In this memoir Ampère “demonstrated for the first time that two parallel conductors, carrying currents traveling in the same direction, attract each other; conversely, if the currents are traveling in opposite directions, they repel each other” (Sparrow, Milestones, p. 33). “The experimental investigation by which Ampére established the laws of the mechanical action between electric currents is one of the most brilliant achievements in science. The whole, theory and experiment, seems as if it had leaped, full grown and full armed, from the brain of the ‘Newton of electricity.’ It is perfect in form, and unassailable in accuracy, and it is summed up in a formula from which all the phenomena may be deduced, and which must always remain the cardinal formula of electro-dynamics.”- Maxwell. “It was the discovery of electromagnetism by Hans Christian Oersted in the spring of 1820 which opened up a whole new world to Ampere and gave him the opportunity to show the full power of his AMPÈRE, André Marie. -
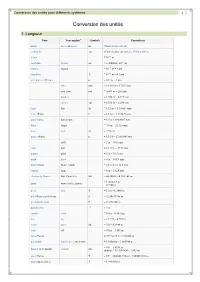
Conversion Des Unités Pour Différents Systèmes 1
Conversion des unités pour différents systèmes 1 Conversion des unités 1. Longueur Nom Nom anglais(1) Symbole Équivalence mètre metre ou meter m (Unité de base du SI) -2 centimètre cm (Unité de base du système CGS) ≡ 10 m -15 fermi ≡ 10 m -13 siegbahn X-unit xu ≈ 1,0000021×10 m -12 stigma stigma ≡ 10 m = 1 pm -10 ångström Å ≡ 10 m = 0,1 nm micromètre, Micron μ ≡ 10-6 m = 1 μm twip twp ≡ 1/1440 in ≈ 17,639 μm mil; thou mil ≡ 0,001 in = 25,4 μm mickey ≡ 1/200 in = 0,127 mm calibre cal ≡ 1/100 in = 0,254 mm ligne line ln ≡ 1/12 in ≈ 2,116667 mm ligne (Paris) l ≡ 1/12 p ≈ 2,255829 mm grain d'orge barleycorn ≡ 1/3 in ≈ 8,466667 mm doigt finger ≡ 7/8 in = 22,225 mm pouce inch in ≡ 2,54 cm pouce (Paris) p ≡ 1/12 P ≈ 27,069949 mm stick ≡ 2 in = 50,8 mm clou nail ≡ 2 1/4 in = 57,15 mm paume palm ≡ 3 in = 76,2 mm main hand ≡ 4 in = 101,6 mm doigt (tissu) finger (cloth) ≡ 4 1/2 in = 114,3 mm empan span ≡ 6 in = 152,4 mm chaînon de Gunter link (Gunter's) lnk ≡ 66/100 ft = 0,201 168 m ≡ 1/4 yd = 9 in quart span (cloth); quarter = 0,2286 m pied foot ft ≡ 12 in = 0,3048 m pied (Paris); pied de roi P ≈ 0,324839385 m pied (québécois) P ≡ 0,3248406 m pas de reine ? ≈ ? m coudée cubit ≡ 18 in = 0,4572 m pas pace ≡ 2 1/2 ft = 0,762 m verge yard yd ≡ 3 ft = 0,9144 m aune ell ≡ 45 in = 1,143 m aune (Paris) ≡ 3 P 7 p 10 l ≈ 1,186566 m pas double double pace; milli-mile ≡ 1/1000 mi = 1,609344 m ≡ 6 ft = 1,8288 m brasse; toise marine fathom fm (parfois ≡ 1/1000 NM = 1,852 m) toise (Paris) T ≡ 6 P = 864/443,296 m ≈ 1,949036310 m toise (québécoise) T ≡ 1,9490436 -

Scientific Travel in the Atlantic World: the French Expedition to Gorée And
BJHS 43(1): 1–17, March 2010. f British Society for the History of Science 2009 doi:10.1017/S0007087409990057 First published online 27 August 2009 Scientific travel in the Atlantic world: the French expedition to Gore´e and the Antilles, 1681–1683 NICHOLAS DEW* Abstract. Although historians have long recognized the importance of long-range scientific expeditions in both the practice and culture of eighteenth- and nineteenth-century science, it is less well understood how this form of scientific organization emerged and became established in the seventeenth and early eighteenth centuries. In the late seventeenth century new European scientific institutions tried to make use of globalized trade networks for their own ends, but to do so proved difficult. This paper offers a case history of one such expedition, the voyage sponsored by the French Acade´mie royale des sciences to Gore´e (in modern Senegal) and the Caribbean islands of Guadeloupe and Martinique in 1681–3. The voyage of Varin, Deshayes and de Glos reveals how the process of travel itself caused problems for instruments and observers alike. Before expeditions From Bacon on, seventeenth-century thinkers often noted the links between the ad- vancement of learning and the expansion of commerce. Yet until recently historians kept these two histories apart. Research of the last few years, however, has uncovered the range of connections between early modern colonial trade and the making of natural knowledge.1 The increasingly global circulation of scientific practices, itself * McGill University, Department of History, 855 rue Sherbrooke ouest, Montre´al, Que´bec, H3A 2T7, Canada.