Structural Equation Modeling and Simultaneous Clustering Through the Partial Least Squares Algorithm
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Overview-Of-Statistical-Analytics-And
Brief Overview of Statistical Analytics and Machine Learning tools for Data Scientists Tom Breur 17 January 2017 It is often said that Excel is the most commonly used analytics tool, and that is hard to argue with: it has a Billion users worldwide. Although not everybody thinks of Excel as a Data Science tool, it certainly is often used for “data discovery”, and can be used for many other tasks, too. There are two “old school” tools, SPSS and SAS, that were founded in 1968 and 1976 respectively. These products have been the hallmark of statistics. Both had early offerings of data mining suites (Clementine, now called IBM SPSS Modeler, and SAS Enterprise Miner) and both are still used widely in Data Science, today. They have evolved from a command line only interface, to more user-friendly graphic user interfaces. What they also share in common is that in the core SPSS and SAS are really COBOL dialects and are therefore characterized by row- based processing. That doesn’t make them inherently good or bad, but it is principally different from set-based operations that many other tools offer nowadays. Similar in functionality to the traditional leaders SAS and SPSS have been JMP and Statistica. Both remarkably user-friendly tools with broad data mining and machine learning capabilities. JMP is, and always has been, a fully owned daughter company of SAS, and only came to the fore when hardware became more powerful. Its initial “handicap” of storing all data in RAM was once a severe limitation, but since computers now have large enough internal memory for most data sets, its computational power and intuitive GUI hold their own. -
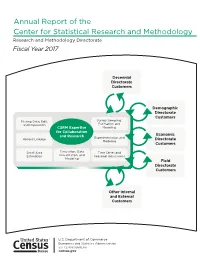
Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017
Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017 Decennial Directorate Customers Demographic Directorate Customers Missing Data, Edit, Survey Sampling: and Imputation Estimation and CSRM Expertise Modeling for Collaboration Economic and Research Experimentation and Record Linkage Directorate Modeling Customers Small Area Simulation, Data Time Series and Estimation Visualization, and Seasonal Adjustment Modeling Field Directorate Customers Other Internal and External Customers ince August 1, 1933— S “… As the major figures from the American Statistical Association (ASA), Social Science Research Council, and new Roosevelt academic advisors discussed the statistical needs of the nation in the spring of 1933, it became clear that the new programs—in particular the National Recovery Administration—would require substantial amounts of data and coordination among statistical programs. Thus in June of 1933, the ASA and the Social Science Research Council officially created the Committee on Government Statistics and Information Services (COGSIS) to serve the statistical needs of the Agriculture, Commerce, Labor, and Interior departments … COGSIS set … goals in the field of federal statistics … (It) wanted new statistical programs—for example, to measure unemployment and address the needs of the unemployed … (It) wanted a coordinating agency to oversee all statistical programs, and (it) wanted to see statistical research and experimentation organized within the federal government … In August 1933 Stuart A. Rice, President of the ASA and acting chair of COGSIS, … (became) assistant director of the (Census) Bureau. Joseph Hill (who had been at the Census Bureau since 1900 and who provided the concepts and early theory for what is now the methodology for apportioning the seats in the U.S. -

Fibrinogen Levels Are Associated with Lymph Node Involvement And
ANTICANCER RESEARCH 38 : 1097-1104 (2018) doi:10.21873/anticanres.12328 Fibrinogen Levels Are Associated with Lymph Node Involvement and Overall Survival in Gastric Cancer Patients JÚLIUS PALAJ 1, ŠTEFAN KEČKÉŠ 2, VÍTĚZSLAV MAREK 1, DANIEL DYTTERT 1, IVETA WACZULÍKOVÁ 3 and ŠTEFAN DURDÍK 1 1Department of Oncological Surgery, St. Elizabeth Cancer Institute, Slovak Republic and Faculty of Medicine in Bratislava of the Comenius University, Bratislava, Slovak Republic; 2Department of Immunodiagnostics, St. Elizabeth Cancer Institute, Bratislava, Slovak Republic; 3Department of Nuclear Physics and Biophysics, Comenius University, Faculty of Mathematics, Physics and Informatics, Bratislava, Slovak Republic Abstract. Background/Aim: Combination of perioperative accounting for 6.8% of all diagnosed cancers and making this chemotherapy with gastrectomy with D2 lymphadenectomy cancer the 5th most common malignancy globally (2). improves long-term survival in patients with gastric cancer. Moreover, it is the third leading cause of death in both sexes The aim of this study was to investigate the predictive value accounting for 8.8% of the total deaths from cancer (3). of preoperative levels of CRP, albumin, fibrinogen, In spite of advancements in chemotherapy and local neutrophil-to-lymphocyte ratio and routinely used tumor control of GC, prognosis remains poor, mainly because of markers (CEA, CA 19-9, CA 72-4) for lymph node the advancement of the disease at the time of diagnosis. involvement. Materials and Methods: This retrospective Approximately 50% patients in western countries have study was conducted in 136 patients who underwent surgery metastases at the time of diagnosis, and from those without between 2007 and 2015. Bivariable and multivariable metastatic disease only 50% are eligible for gastric resection analyses were performed in order to identify important (4). -

Towards a Fully Automated Extraction and Interpretation of Tabular Data Using Machine Learning
UPTEC F 19050 Examensarbete 30 hp August 2019 Towards a fully automated extraction and interpretation of tabular data using machine learning Per Hedbrant Per Hedbrant Master Thesis in Engineering Physics Department of Engineering Sciences Uppsala University Sweden Abstract Towards a fully automated extraction and interpretation of tabular data using machine learning Per Hedbrant Teknisk- naturvetenskaplig fakultet UTH-enheten Motivation A challenge for researchers at CBCS is the ability to efficiently manage the Besöksadress: different data formats that frequently are changed. Significant amount of time is Ångströmlaboratoriet Lägerhyddsvägen 1 spent on manual pre-processing, converting from one format to another. There are Hus 4, Plan 0 currently no solutions that uses pattern recognition to locate and automatically recognise data structures in a spreadsheet. Postadress: Box 536 751 21 Uppsala Problem Definition The desired solution is to build a self-learning Software as-a-Service (SaaS) for Telefon: automated recognition and loading of data stored in arbitrary formats. The aim of 018 – 471 30 03 this study is three-folded: A) Investigate if unsupervised machine learning Telefax: methods can be used to label different types of cells in spreadsheets. B) 018 – 471 30 00 Investigate if a hypothesis-generating algorithm can be used to label different types of cells in spreadsheets. C) Advise on choices of architecture and Hemsida: technologies for the SaaS solution. http://www.teknat.uu.se/student Method A pre-processing framework is built that can read and pre-process any type of spreadsheet into a feature matrix. Different datasets are read and clustered. An investigation on the usefulness of reducing the dimensionality is also done. -

An Example of Statistical Data Analysis Using the R Environment for Statistical Computing
Tutorial: An example of statistical data analysis using the R environment for statistical computing D G Rossiter Version 1.4; May 6, 2017 Subsoil vs. topsoil clay, by zone Regression Residuals vs. Fitted Values, subsoil clay % 128 80 15 138 ● 17119 137 1 ● 139 70 2 ● 3 10 ● 4 ● 60 ● ● 5 50 0 Slopes: Residual 40 zone 1 : 0.834 Subsoil clay % Subsoil clay ● ● zone 2 : 0.739 zone 3 : 0.564 −5 30 zone 4 : 1.081 overall: 0.829 −10 20 81 −15 10 145 10 20 30 40 50 60 70 80 20 30 40 50 60 70 Topsoil clay % Fitted GLS 2nd−order trend surface, subsoil clay % 340000 335000 330000 N 325000 320000 315000 660000 670000 680000 690000 700000 E Copyright © D G Rossiter 2008 { 2010, 2014, 2017 All rights reserved. Repro- duction and dissemination of the work as a whole (not parts) freely permitted if this original copyright notice is included. Sale or placement on a web site where payment must be made to access this document is strictly prohibited. To adapt or translate please contact the author ([email protected]). Contents 1 Introduction1 2 Example Data Set2 2.1 Loading the dataset...........................3 2.2 A normalized database structure*...................5 3 Research questions8 4 Univariarte Analysis9 4.1 Univariarte Exploratory Data Analysis................9 4.2 Point estimation; inference of the mean............... 14 4.3 Answers.................................. 15 5 Bivariate correlation and regression 16 5.1 Conceptual issues in correlation and regression........... 16 5.2 Bivariate Exploratory Data Analysis................. 18 5.3 Bivariate Correlation Analysis..................... 22 5.4 Fitting a regression line........................ -

Using SPSS to Analyze Complex Survey Data: a Primer
Journal of Modern Applied Statistical Methods Volume 18 Issue 1 Article 16 4-6-2020 Using SPSS to Analyze Complex Survey Data: A Primer Danjie Zou University of British Columbia, [email protected] Jennifer E. V. Lloyd University of British Columbia, [email protected] Jennifer L. Baumbusch University of British Columbia, [email protected] Follow this and additional works at: https://digitalcommons.wayne.edu/jmasm Part of the Applied Statistics Commons, Social and Behavioral Sciences Commons, and the Statistical Theory Commons Recommended Citation Zou, D., Lloyd, J. E. V., & Baumbusch, J. L. (2019). Using SPSS to analyze complex survey data: A primer Journal of Modern Applied Statistical Methods, 18(1), eP3253. doi: 10.22237/jmasm/1556670300 This Regular Article is brought to you for free and open access by the Open Access Journals at DigitalCommons@WayneState. It has been accepted for inclusion in Journal of Modern Applied Statistical Methods by an authorized editor of DigitalCommons@WayneState. Using SPSS to Analyze Complex Survey Data: A Primer Cover Page Footnote Thank you to the McCreary Centre Society (https://www.mcs.bc.ca/), who collects and owns the British Columbia Adolescent Health Survey data. Thanks also to Dr. Colleen Poon, Allysha Ram, Dr. Elizabeth Saewyc, and Annie Smith for their guidance as we worked with the data. We also thank the Social Sciences and Humanities Research Council of Canada (SSHRC) for an Insight Development grant awarded to Dr. Baumbusch. Finally, thanks to blind reviewers for their comments that improved the paper. An SPSS syntax file with the commands outlined in this paper is va ailable for download at: http://blogs.ubc.ca/jenniferlloyd/ This regular article is available in Journal of Modern Applied Statistical Methods: https://digitalcommons.wayne.edu/ jmasm/vol18/iss1/16 Journal of Modern Applied Statistical Methods May 2019, Vol. -

Real-Time Process Monitoring and Statistical Process Control for an Automated Casting Facility
Project Number: SYS-SYS7 Real-Time Process Monitoring And Statistical Process Control For an Automated Casting Facility A Major Qualifying Project Report Submitted to the Faculty Of WORCESTER POLYTECHNIC INSTITUTE In partial fulfillment of the requirements for the Degree of Bachelor of Science In Mechanical Engineering By Daniel Lettiere Date: June 2012 Approved: Prof. Satya Shivkumar, Advisor 1 Contents Abstract ......................................................................................................................................4 1. Introduction ............................................................................................................................5 2. Background .............................................................................................................................7 2.1 Manufacturing of Investment Castings .............................................................................7 2.1.1 Origins ........................................................................................................................7 2.1.2 Defects .......................................................................................................................9 2.1.3 Effects of Humidity .....................................................................................................9 2.1.4 Effects of Temperature .............................................................................................10 2.1.5 Effects of Time ..........................................................................................................10 -

Statistics with Free and Open-Source Software
Free and Open-Source Software • the four essential freedoms according to the FSF: • to run the program as you wish, for any purpose • to study how the program works, and change it so it does Statistics with Free and your computing as you wish Open-Source Software • to redistribute copies so you can help your neighbor • to distribute copies of your modified versions to others • access to the source code is a precondition for this Wolfgang Viechtbauer • think of ‘free’ as in ‘free speech’, not as in ‘free beer’ Maastricht University http://www.wvbauer.com • maybe the better term is: ‘libre’ 1 2 General Purpose Statistical Software Popularity of Statistical Software • proprietary (the big ones): SPSS, SAS/JMP, • difficult to define/measure (job ads, articles, Stata, Statistica, Minitab, MATLAB, Excel, … books, blogs/posts, surveys, forum activity, …) • FOSS (a selection): R, Python (NumPy/SciPy, • maybe the most comprehensive comparison: statsmodels, pandas, …), PSPP, SOFA, Octave, http://r4stats.com/articles/popularity/ LibreOffice Calc, Julia, … • for programming languages in general: TIOBE Index, PYPL, GitHut, Language Popularity Index, RedMonk Rankings, IEEE Spectrum, … • note that users of certain software may be are heavily biased in their opinion 3 4 5 6 1 7 8 What is R? History of S and R • R is a system for data manipulation, statistical • … it began May 5, 1976 at: and numerical analysis, and graphical display • simply put: a statistical programming language • freely available under the GNU General Public License (GPL) → open-source -

STAT 3304/5304 Introduction to Statistical Computing
STAT 3304/5304 Introduction to Statistical Computing Statistical Packages Some Statistical Packages • BMDP • GLIM • HIL • JMP • LISREL • MATLAB • MINITAB 1 Some Statistical Packages • R • S-PLUS • SAS • SPSS • STATA • STATISTICA • STATXACT • . and many more 2 BMDP • BMDP is a comprehensive library of statistical routines from simple data description to advanced multivariate analysis, and is backed by extensive documentation. • Each individual BMDP sub-program is based on the most competitive algorithms available and has been rigorously field-tested. • BMDP has been known for the quality of it’s programs such as Survival Analysis, Logistic Regression, Time Series, ANOVA and many more. • The BMDP vendor was purchased by SPSS Inc. of Chicago in 1995. SPSS Inc. has stopped all develop- ment work on BMDP, choosing to incorporate some of its capabilities into other products, primarily SY- STAT, instead of providing further updates to the BMDP product. • BMDP is now developed by Statistical Solutions and the latest version (BMDP 2009) features a new mod- ern user-interface with all the statistical functionality of the classic program, running in the latest MS Win- dows environments. 3 LISREL • LISREL is software for confirmatory factor analysis and structural equation modeling. • LISREL is particularly designed to accommodate models that include latent variables, measurement errors in both dependent and independent variables, reciprocal causation, simultaneity, and interdependence. • Vendor information: Scientific Software International http://www.ssicentral.com/ 4 MATLAB • Matlab is an interactive, matrix-based language for technical computing, which allows easy implementation of statistical algorithms and numerical simulations. • Highlights of Matlab include the number of toolboxes (collections of programs to address specific sets of problems) available. -
Statistica 12 Crack Serial 13
1 / 3 Statistica 12 Crack Serial 13 Jun 17, 2020 — Found results for Statistica 12 crack, serial & keygen. ... adobe photoshop cs5 extended crack 11.. TUTORIAL DE INSTALAÇÃO DO STATISTICA 12.5.. Statistica 13.1 - June 2016; Statistica 13.2 - Sep 30, 2016; Statistica 13.3 - June, 2017; Statistica 13.3.1 .... Download the free trial today, skim through the response surface tutorial provided under 'Help', and see for yourself. Latest Release: Version 13! The release .... Systat Software proudly introduces SYSTAT 13, the latest advancement in desktop statistical computing. Novice statistical users can use SYSTAT's menu-driven .... 5 days ago — STATISTICA is a data analysis and visualization program ... StatSoft. Review Comments (21) Questions & Answers (12).. Mar 7, 2017 — There Is No Preview Available For This Item. This item does not appear to have any files that can be experienced on Archive.org.. T1: STATISTICA Registration File P1: STATISTICA Concurrent C0: ... contact (required): IT SUPPORT R12: Software is for personal use: 0 R13: Receive product .... Sep 18, 2018 — ScreenShots: Software Description: The Enterprise line of STATISTICA products isdesigned for multi-user, collaborative analytic applications .... Jan 27, 2021 — Statistica 12 Crack Serial 13. job 12 13 StatSoft STATISTICA 12.51.6 Gb StatSoft12.5 . ... zte mf6xx exploit researcher free 11lkjh.. Link download StatSoft STATISTICA 12.5.192.7 x64 full cracked forever ... Description: STATISTICA is a statistical data analysis system that includes a wide ... Mar 13, 2020 — Statistica 12 Crack Serial 13 - http://fancli.com/183ahi 45565b7e23 4th Down Conversions, 8/12, 7/10. Total Offensive . Field Goals, 19/22, .... Feb 20, 2018 — 软件简介STATISTICA是美国STAT SOFT公司开发的大型统计软件,该公司与2014年3月被戴尔公司收购。该软件的功能包含统计功能、数据挖掘功能以及统计绘图 ... -

Curriculum Vitae Europass
Curriculum Vitae Personal Information First name/Last name Giovanni Sotgiu Clinical Epidemiology and Medical Statistics Unit, Department of Biomedical Sciences - Address University of Sassari – Via Padre Manzella, 4. Sassari – 07100, Italy Telephone(s) +39 079 22 9959 Fax +39 079 22 8472 E-mail(s) [email protected]; [email protected] Nationality Italian Date of Birth 30/August/1972 1996-1997: Medical Degree (110/110 cum laude); 2000-2001: Specialization in Infectious Diseases (50/50 cum laude); 2003-2004: PhD in “Methodology of Clinical Trials” (Excellent); Degree/Specialization/PhD 2006-2007: Specialization in Medical Statistics (50/50 cum laude). 2014-2015: Executive Master in Management of Health and Social Care Organizations. 2016: Fellow of European Respiratory Society (FERS) Academic Position 2016-2017: Full Professor of Medical Statistics – University of Sassari, Italy. 2009-2010: Associate Professor – University of Sassari, Italy. 2004-2005: Assistant Professor – University of Sassari, Italy. Scientific Sector 06/M1 –Medical Statistics/MED-01 Sweden/European Centre for Disease Prevention and Control. Foreign Activity Public Health Activities in several European and non-European countries (Ukraine, Bolivia, Macedonia, Portugal, Albania, Zimbabwe, Latvia, etc.). Pagina 1/6 - Curriculum vitae_ Sotgiu Giovanni Teaching Professor of the following medical disciplines in undergraduate and graduate courses, University of Sassari, Italy: -Preventive and Community Nursing; -Hygiene and Preventive Medicine; -Hygiene and Epidemiological -

Funkcie Programu Microsoft Excel (Add-In) Na Analýzu Kontingenčných Tabuliek (Analýza Početností a Proporcií)
Funkcie programu Microsoft Excel (add-in) na analýzu kontingenčných tabuliek (analýza početností a proporcií) Peter Slezák 1, Pavol Námer 2, Iveta Waczulíková 2 1Ústav normálnej a patologickej fyziológie SAV, Sienkiewiczova 1, 813 71 Bratislava, 2Fakulta matematiky fyziky a informatiky UK, Mlynská dolina F1, 842 48 Bratislava S pomocou Excel Visual Basic for Application (VBA), sme vyvinuli nástroj obsahujúci funkcie, ktoré počítajú najrelevantnejšie štatistické testy používané pri analýze kontingenčných/frekvenčných tabuliek. Tieto funkcie môžu by nainštalované pomocou vytvoreného Excelovského doplnku (Contingency Table (v. 2010).xlam verziu Excelu 2010 prip. Contingency Table (v. 2007).xlm pre staršie verzie). Demonštrácia využitia vytvorených funkcií je k dispozícii vo forme videa: http://www.youtube.com/watch?v=aiF-FYX6b6g. Podrobnejšie matematické informácie o implementovaných metódach sú k dispozícií na stránkach http://bio-med-stat.webnode.sk/ms-excel-add-ins/ , odkiaľ je možné doplnok voľne stiahnuť. Excel function statistical test/method computed Prezentovaný doplnok bol vytvorený pre osobné Chi2 statistics; two-sided P-value; Cramer’s V; Pearson využitie a na edukačné účely. Prehľad štatistických Chi2TESTindependence Contingency coefficient C; coefficient Phi metód a funkcií, v ktorých sú implementované sú one- and two-sided P-value; one- and two-sided mid-P zosumarizované v tabuľke. Pri porovnaní presnosti FisherExactTEST value výsledkov, ktoré prezentované funkcie dosahujú v RiskRatio RR (95% CI) porovnaní s štatistickými programami StatsDirect 2.7.9 (StatsDirect Ltd. StatsDirect statistical software. OddsRatio OR and 95% CI based on Woolf or Cornfield method http://www.statsdirect.com ), Statistica 11 (StatSoft, Chi2 statistics and two-sided P-value for linear trend; Inc. (2012) STATISTICA (data analysis software CochranArmitageTEST Chi2 statistics a two-sided P-value for departure from system), version 11.