Lecture Notes #15 --- Approximation Theory --- the Fast Fourier
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bring Down the Two-Language Barrier with Julia Language for Efficient
AbstractSDRs: Bring down the two-language barrier with Julia Language for efficient SDR prototyping Corentin Lavaud, Robin Gerzaguet, Matthieu Gautier, Olivier Berder To cite this version: Corentin Lavaud, Robin Gerzaguet, Matthieu Gautier, Olivier Berder. AbstractSDRs: Bring down the two-language barrier with Julia Language for efficient SDR prototyping. IEEE Embedded Systems Letters, Institute of Electrical and Electronics Engineers, 2021, pp.1-1. 10.1109/LES.2021.3054174. hal-03122623 HAL Id: hal-03122623 https://hal.archives-ouvertes.fr/hal-03122623 Submitted on 27 Jan 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. AbstractSDRs: Bring down the two-language barrier with Julia Language for efficient SDR prototyping Corentin LAVAUD∗, Robin GERZAGUET∗, Matthieu GAUTIER∗, Olivier BERDER∗. ∗ Univ Rennes, CNRS, IRISA, [email protected] Abstract—This paper proposes a new methodology based glue interface [8]. Regarding programming semantic, low- on the recently proposed Julia language for efficient Software level languages (e.g. C++/C, Rust) offers very good runtime Defined Radio (SDR) prototyping. SDRs are immensely popular performance but does not offer a good prototyping experience. as they allow to have a flexible approach for sounding, monitoring or processing radio signals through the use of generic analog High-level languages (e.g. -

SEISGAMA: a Free C# Based Seismic Data Processing Software Platform
Hindawi International Journal of Geophysics Volume 2018, Article ID 2913591, 8 pages https://doi.org/10.1155/2018/2913591 Research Article SEISGAMA: A Free C# Based Seismic Data Processing Software Platform Theodosius Marwan Irnaka, Wahyudi Wahyudi, Eddy Hartantyo, Adien Akhmad Mufaqih, Ade Anggraini, and Wiwit Suryanto Seismology Research Group, Physics Department, Faculty of Mathematics and Natural Sciences, Universitas Gadjah Mada, Sekip Utara Bulaksumur, Yogyakarta 55281, Indonesia Correspondence should be addressed to Wiwit Suryanto; [email protected] Received 4 July 2017; Accepted 24 December 2017; Published 30 January 2018 Academic Editor: Filippos Vallianatos Copyright © 2018 Teodosius Marwan Irnaka et al. Tis is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Seismic refection is one of the most popular methods in geophysical prospecting. Nevertheless, obtaining high resolution and accurate results requires a sophisticated processing stage. Tere are many open-source seismic refection data processing sofware programs available; however, they ofen use a high-level programming language that decreases its overall performance, lacks intuitive user-interfaces, and is limited to a small set of tasks. Tese shortcomings reveal the need to develop new sofware using a programming language that is natively supported by Windows5 operating systems, which uses a relatively medium-level programming language (such as C#) and can be enhanced by an intuitive user interface. SEISGAMA was designed to address this need and employs a modular concept, where each processing group is combined into one module to ensure continuous and easy development and documentation. -

Julia: a Modern Language for Modern ML
Julia: A modern language for modern ML Dr. Viral Shah and Dr. Simon Byrne www.juliacomputing.com What we do: Modernize Technical Computing Today’s technical computing landscape: • Develop new learning algorithms • Run them in parallel on large datasets • Leverage accelerators like GPUs, Xeon Phis • Embed into intelligent products “Business as usual” will simply not do! General Micro-benchmarks: Julia performs almost as fast as C • 10X faster than Python • 100X faster than R & MATLAB Performance benchmark relative to C. A value of 1 means as fast as C. Lower values are better. A real application: Gillespie simulations in systems biology 745x faster than R • Gillespie simulations are used in the field of drug discovery. • Also used for simulations of epidemiological models to study disease propagation • Julia package (Gillespie.jl) is the state of the art in Gillespie simulations • https://github.com/openjournals/joss- papers/blob/master/joss.00042/10.21105.joss.00042.pdf Implementation Time per simulation (ms) R (GillespieSSA) 894.25 R (handcoded) 1087.94 Rcpp (handcoded) 1.31 Julia (Gillespie.jl) 3.99 Julia (Gillespie.jl, passing object) 1.78 Julia (handcoded) 1.2 Those who convert ideas to products fastest will win Computer Quants develop Scientists prepare algorithms The last 25 years for production (Python, R, SAS, DEPLOY (C++, C#, Java) Matlab) Quants and Computer Compress the Scientists DEPLOY innovation cycle collaborate on one platform - JULIA with Julia Julia offers competitive advantages to its users Julia is poised to become one of the Thank you for Julia. Yo u ' v e k i n d l ed leading tools deployed by developers serious excitement. -

Praktikum Iz Softverskih Alata U Elektronici
PRAKTIKUM IZ SOFTVERSKIH ALATA U ELEKTRONICI 2017/2018 Predrag Pejović 31. decembar 2017 Linkovi na primere: I OS I LATEX 1 I LATEX 2 I LATEX 3 I GNU Octave I gnuplot I Maxima I Python 1 I Python 2 I PyLab I SymPy PRAKTIKUM IZ SOFTVERSKIH ALATA U ELEKTRONICI 2017 Lica (i ostali podaci o predmetu): I Predrag Pejović, [email protected], 102 levo, http://tnt.etf.rs/~peja I Strahinja Janković I sajt: http://tnt.etf.rs/~oe4sae I cilj: savladavanje niza programa koji se koriste za svakodnevne poslove u elektronici (i ne samo elektronici . ) I svi programi koji će biti obrađivani su slobodan softver (free software), legalno možete da ih koristite (i ne samo to) gde hoćete, kako hoćete, za šta hoćete, koliko hoćete, na kom računaru hoćete . I literatura . sve sa www, legalno, besplatno! I zašto svake godine (pomalo) updated slajdovi? Prezentacije predmeta I engleski I srpski, kraća verzija I engleski, prezentacija i animacije I srpski, prezentacija i animacije A šta se tačno radi u predmetu, koji programi? 1. uvod (upravo slušate): organizacija nastave + (FS: tehnička, ekonomska i pravna pitanja, kako to uopšte postoji?) (≈ 1 w) 2. operativni sistem (GNU/Linux, Ubuntu), komandna linija (!), shell scripts, . (≈ 1 w) 3. nastavak OS, snalaženje, neki IDE kao ilustracija i vežba, jedan Python i jedan C program . (≈ 1 w) 4.L ATEX i LATEX 2" (≈ 3 w) 5. XCircuit (≈ 1 w) 6. probni kolokvijum . (= 1 w) 7. prvi kolokvijum . 8. GNU Octave (≈ 1 w) 9. gnuplot (≈ (1 + ) w) 10. wxMaxima (≈ 1 w) 11. drugi kolokvijum . 12. Python, IPython, PyLab, SymPy (≈ 3 w) 13. -

Introduction to Matlab
Introduction to Numerical Libraries Shaohao Chen High performance computing @ Louisiana State University Outline 1. Introduction: why numerical libraries? 2. Fast Fourier transform: FFTw 3. Linear algebra libraries: LAPACK 4. Krylov subspace solver: PETSc 5. GNU scientific libraries: GSL 1. Introduction It is very easy to write bad code! • Loops : branching, dependencies • I/O : resource conflicts, • Memory : long fetch-time • Portability : code and data portable? • Readability : Can you still understand it? A solution: look for existing libraries! Why numerical libraries? • Many functions or subroutines you need may have already been coded by others. Just use them. • Not necessary to code every line by yourself. • Check available libs before starting to write your program. • Save your time and efforts! Advantages of using numerical libraries: • Computing optimizations • Portability • Easy to debug • Easy to read What you will learn in this training • General knowledge of numerical libs. • How to check available libs on HPC systems and the web. • How to use numerical libs on HPC systems. • Basic programming with numerical libs. List of notable numerical libraries • Linear Algebra Package (LAPACK): computes matrix and vector operations. [Fortran] • Fastest Fourier Transform in the West (FFTW): computes Fourier and related transforms. [C/C++] • GNU Scientific Library (GSL): provides a wide range of mathematical routines. [C/C++] • Portable, Extensible Toolkit for Scientific Computation (PETSc): a suite of data structures and routines for the scalable (parallel) solution of scientific applications modeled by partial differential equations. [C/C++] • NumPy: adds support for the manipulation of large, multi-dimensional arrays and matrices; also includes a large collection of high-level mathematical functions. -

Fastest Fourier Transform in the West
Fastest Fourier Transform in the West Devendra Ghate and Nachi Gupta [email protected], [email protected] Oxford University Computing Laboratory MT 2006 Internal Seminar – p. 1/33 Cooley-Tukey Algorithm for FFT N 1 2πi − nk Xk = X xne− N ; k = 0; : : : ; N − 1 n=0 2 If we solve for Xk directly then O(N ) operations required for the solution. If N = p × q, then this transformation can be split into two separate transformations... ...recursively, we get the FFT algorithm. N If N is split into r intervals of r each then the complexity is r × N × logr N. This can be generalised to mixed-radix algorithms. MT 2006 Internal Seminar – p. 2/33 Overview of FFT algorithms Cooley-Tukey FFT algorithm (popularized in 1965), known by Gauss in 1805. Prime-factor FFT algorithm ± a.k.a. Good-Thomas (1958-1963), N = N1N2 becomes 2D N1 by N2 DFT for only relatively prime N1; N2. Bruun's FFT algorithm (1978, generalized to arbitrary even composite sizes by H. Murakami in 1996), recursive polynomial factorization approach. Rader's FFT algorithm (1968), for prime size by expressing DFT as a convolution. Bluestein's FFT algorithm (1968) ± a.k.a. chirp z-transform algorithm (1969), for prime sizes by expressing DFT as a convolution. Rader-Brenner (1976) ± Cooley-Tukey like, but purely imag twiddle factors MT 2006 Internal Seminar – p. 3/33 What is FFTW? FFTW is a package for computing a one or multidimensional complex discrete Fourier transform (DFT) of arbitrary size. At the heart of FFTW lies a philosophy geared towards speed, portability, and elegance – achieved via an adaptive software architecture. -
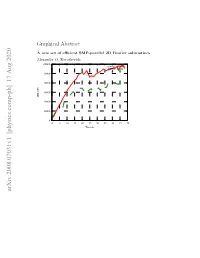
A New Set of Efficient SMP-Parallel 2D Fourier Subroutines
Graphical Abstract A new set of efficient SMP-parallel 2D Fourier subroutines Alexander O. Korotkevich 60000 new lib FFTW 50000 40000 30000 MFLOPs 20000 10000 0 0 5 10 15 20 25 30 35 40 45 50 Threads arXiv:2008.07031v1 [physics.comp-ph] 17 Aug 2020 Highlights A new set of efficient SMP-parallel 2D Fourier subroutines Alexander O. Korotkevich • New set of efficient SMP-parallel DFTs • Free software license • Significant performance boost for large sizes of arrays. A new set of efficient SMP-parallel 2D Fourier subroutines Alexander O. Korotkevicha,b aDepartment of Mathematics & Statistics, The University of New Mexico, MSC01 1115, 1 University of New Mexico, Albuquerque, New Mexico, 87131-0001, USA bL. D. Landau Institute for Theoretical Physics, 2 Kosygin Str., Moscow, 119334, Russian Federation Abstract Extensive set of tests on different platforms indicated that there is a per- formance drop of current standard de facto software library for the Dis- crete Fourier Transform (DFT) in case of large 2D array sizes (larger than 16384 × 16384). Parallel performance for Symmetric Multi Processor (SMP) systems was seriously affected. The remedy for this problem was proposed and implemented as a software library for 2D out of place complex to complex DFTs. Proposed library was thoroughly tested on different available architec- tures and hardware configurations and demonstrated significant (38 − 94%) performance boost on vast majority of them. The new library together with the testing suite and results of all tests is published as a project on GitHub.com platform under free software license (GNU GPL v3). Com- prehensive description of programming interface as well as provided testing programs is given. -

2019 Julia User & Developer Survey
User & Developer Survey 2019 Viral B. Shah Andrew Claster Abhijith Chandraprabhu Methodology We conducted 1,834 interviews online among Julia users and developers June 12-24, 2019 Margin of error is +/- 2.3 percentage points We recruited respondents online using Slack, Discourse, Twitter, email, JuliaLang.org and JuliaComputing.com The survey was administered only in English, but more than half of respondents come from non-English speaking countries 2 56% of Respondents Use Julia a ‘Great Deal’ While 38% Use Julia ‘Some’ Python and Bash/Shell/PowerShell are 2nd and 3rd among Julia Users and Developers How frequently do you use each of the following languages? Great deal Some Julia 56% 38% 94% Python 39% 42% 81% Bash/Shell/PowerShell 23% 46% 69% MATLAB 16% 27% 43% C++ 11% 29% 40% C 8% 32% 40% R 15% 23% 38% SQL 11% 23% 34% JavaScript 6% 21% 27% Java 5% 13% 18% C# 2% 6% 8% Scala 1%5 % 6% 3 93% of Respondents Like Julia or Say Julia Is One of Their Favorite Languages Python Comes Second Among Julia Users and Developers How much do you like each of the following languages? One of my favorite languages Like Julia 73% 20% 93% Python 26% 35% 61% C 6% 21% 27% R 9% 14% 23% Matlab 8% 15% 23% C++ 6% 17% 23% Bash/Shell/PowerShell 4% 18% 22% SQL 3% 13% 16% JavaScript 2% 9% 11% Java 2% 8% 10% C# 2% 7% 9% Scala 2% 5% 7% 4 The MOST Popular TECHNICAL Features of Julia Are Speed/Performance, Ease of Use, Open Source, Multiple Dispatch and Solving the Two Language Problem Thinking only about the TECHNICAL aspects or features of Julia, what are the TECHNICAL -

Pipenightdreams Osgcal-Doc Mumudvb Mpg123-Alsa Tbb
pipenightdreams osgcal-doc mumudvb mpg123-alsa tbb-examples libgammu4-dbg gcc-4.1-doc snort-rules-default davical cutmp3 libevolution5.0-cil aspell-am python-gobject-doc openoffice.org-l10n-mn libc6-xen xserver-xorg trophy-data t38modem pioneers-console libnb-platform10-java libgtkglext1-ruby libboost-wave1.39-dev drgenius bfbtester libchromexvmcpro1 isdnutils-xtools ubuntuone-client openoffice.org2-math openoffice.org-l10n-lt lsb-cxx-ia32 kdeartwork-emoticons-kde4 wmpuzzle trafshow python-plplot lx-gdb link-monitor-applet libscm-dev liblog-agent-logger-perl libccrtp-doc libclass-throwable-perl kde-i18n-csb jack-jconv hamradio-menus coinor-libvol-doc msx-emulator bitbake nabi language-pack-gnome-zh libpaperg popularity-contest xracer-tools xfont-nexus opendrim-lmp-baseserver libvorbisfile-ruby liblinebreak-doc libgfcui-2.0-0c2a-dbg libblacs-mpi-dev dict-freedict-spa-eng blender-ogrexml aspell-da x11-apps openoffice.org-l10n-lv openoffice.org-l10n-nl pnmtopng libodbcinstq1 libhsqldb-java-doc libmono-addins-gui0.2-cil sg3-utils linux-backports-modules-alsa-2.6.31-19-generic yorick-yeti-gsl python-pymssql plasma-widget-cpuload mcpp gpsim-lcd cl-csv libhtml-clean-perl asterisk-dbg apt-dater-dbg libgnome-mag1-dev language-pack-gnome-yo python-crypto svn-autoreleasedeb sugar-terminal-activity mii-diag maria-doc libplexus-component-api-java-doc libhugs-hgl-bundled libchipcard-libgwenhywfar47-plugins libghc6-random-dev freefem3d ezmlm cakephp-scripts aspell-ar ara-byte not+sparc openoffice.org-l10n-nn linux-backports-modules-karmic-generic-pae -

FFTW User's Manual
FFTW User's Manual For version 2.1.5, 16 March 2003 Matteo Frigo Steven G. Johnson Copyright c 1997{1999 Massachusetts Institute of Technology. Permission is granted to make and distribute verbatim copies of this manual provided the copyright notice and this permission notice are preserved on all copies. Permission is granted to copy and distribute modified versions of this manual under the con- ditions for verbatim copying, provided that the entire resulting derived work is distributed under the terms of a permission notice identical to this one. Permission is granted to copy and distribute translations of this manual into another lan- guage, under the above conditions for modified versions, except that this permission notice may be stated in a translation approved by the Free Software Foundation. i Table of Contents 1 Introduction............................... 1 2 Tutorial ................................... 3 2.1 Complex One-dimensional Transforms Tutorial ............ 3 2.2 Complex Multi-dimensional Transforms Tutorial ........... 4 2.3 Real One-dimensional Transforms Tutorial ................ 6 2.4 Real Multi-dimensional Transforms Tutorial ............... 7 2.5 Multi-dimensional Array Format ........................ 11 2.5.1 Row-major Format ............................ 11 2.5.2 Column-major Format ......................... 11 2.5.3 Static Arrays in C ............................. 11 2.5.4 Dynamic Arrays in C .......................... 12 2.5.5 Dynamic Arrays in C|The Wrong Way ......... 12 2.6 Words of Wisdom ...................................... 13 2.6.1 Caveats in Using Wisdom ...................... 14 2.6.2 Importing and Exporting Wisdom .............. 14 3 FFTW Reference ......................... 17 3.1 Data Types ............................................ 17 3.2 One-dimensional Transforms Reference................... 18 3.2.1 Plan Creation for One-dimensional Transforms .. -

Introduction to Matlab
Numerical Libraries with C or Fortran Shaohao Chen Research Computing, IS&T, Boston University Outline 1. Overview: What? Why? How to? 2. Fast Fourier transform: FFTw 3. Linear algebra libraries: LAPACK/BLAS 4. Intel Math Kernel Library (MKL) 5. Krylov subspace solver: PETSc 6. GNU scientific libraries (GSL) 1. Overview What you will learn today • Basic knowledge of numerical libraries. • How to check available libraries on BU SCC. • How to use numerical libraries on BU SCC. • Basic programming with several numerical libraries: FFTw, LAPACK/BLAS, MKL, PETSc, GSL What is numerical library? • What is the definition of a library in computer science? In computer science, a library is a collection of non-volatile resources used by computer programs, often to develop software. These may include configuration data, documentation, help data, message templates, pre-written code and subroutines, classes, values or type specifications. (from wiki) • What is numerical library? Numerical library is collection of functions, subroutines or classes that implement mathematical or numerical methods for a certain subject. Usually these functions or routines are common and can be used to build computer programs for various research fields. Several widely-used numerical libraries • Fastest Fourier Transform in the West (FFTW) computes Fourier and related transforms. Written in C. Fortran interface is available. • Basic Linear Algebra Subprograms (BLAS) performs basic vector and matrix operations. Linear Algebra Package (LAPACK) provides linear algebra routines based on BLAS. Written in Fortran. C interface (CBLAS/LAPACKE) is available. • Intel Math Kernel Library (MKL) includes optimized LAPACK, BLAS, FFT, Vector Math and Statistics functions. C/C++ and Fortran interfaces are available. -

Parallelized Simulation Code for Multiconjugate Adaptive Optics
PROCEEDINGS OF SPIE SPIEDigitalLibrary.org/conference-proceedings-of-spie Parallelized simulation code for multiconjugate adaptive optics Aron J. Ahmadia, Brent L. Ellerbroek Aron J. Ahmadia, Brent L. Ellerbroek, "Parallelized simulation code for multiconjugate adaptive optics," Proc. SPIE 5169, Astronomical Adaptive Optics Systems and Applications, (24 December 2003); doi: 10.1117/12.506553 Event: Optical Science and Technology, SPIE's 48th Annual Meeting, 2003, San Diego, California, United States Downloaded From: https://www.spiedigitallibrary.org/conference-proceedings-of-spie on 6/29/2018 Terms of Use: https://www.spiedigitallibrary.org/terms-of-use Parallelized Simulation Code for Multiconjugate Adaptive Optics A.J. Ahmadiaa and B.L. Ellerbroekb aGemini Observatory, 670 N. A’ohoku Place, Hilo, HI 96720 bAURA New Initiatives Offices, 950 N. Cherry Avenue, Tucson, AZ 85719 ABSTRACT Advances in adaptive optics (AO) systems are necessary to achieve optical performance that is suitable for future extremely large telescopes (ELTs). Accurate simulation of system performance during the design process is essential. We detail the current implementation and near-term development plans for a coarse-grain parallel code for simulations of multiconjugate adaptive optics (MCAO). Included is a summary of the simulation’s computationally intensive mathematical subroutines and the associated scaling laws that quantify the size of the computational burden as a function of the simulation parameters. The current state of three different approaches to parallelizing the original serial code is outlined, and the timing results of all three approaches are demonstrated. The first approach, coarse- grained parallelization of the atmospheric propagations, divides the tasks of propagating wavefronts through the atmosphere among a group of processors.