HISTORY-DEPENDENT DIFFERENTIAL VARIATIONAL-HEMIVARIATIONAL INEQUALITIES with APPLICATIONS to CONTACT MECHANICS Zhenhai Liu Van T
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Complete Collection of Chinese Institutes and Universities For
Study in China——All China Universities All China Universities 2019.12 Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities Anhui 安徽 【www.studyinanhui.com】 1. Anhui University 安徽大学 http://ahu.admissions.cn 2. University of Science and Technology of China 中国科学技术大学 http://ustc.admissions.cn 3. Hefei University of Technology 合肥工业大学 http://hfut.admissions.cn 4. Anhui University of Technology 安徽工业大学 http://ahut.admissions.cn 5. Anhui University of Science and Technology 安徽理工大学 http://aust.admissions.cn 6. Anhui Engineering University 安徽工程大学 http://ahpu.admissions.cn 7. Anhui Agricultural University 安徽农业大学 http://ahau.admissions.cn 8. Anhui Medical University 安徽医科大学 http://ahmu.admissions.cn 9. Bengbu Medical College 蚌埠医学院 http://bbmc.admissions.cn 10. Wannan Medical College 皖南医学院 http://wnmc.admissions.cn 11. Anhui University of Chinese Medicine 安徽中医药大学 http://ahtcm.admissions.cn 12. Anhui Normal University 安徽师范大学 http://ahnu.admissions.cn 13. Fuyang Normal University 阜阳师范大学 http://fynu.admissions.cn 14. Anqing Teachers College 安庆师范大学 http://aqtc.admissions.cn 15. Huaibei Normal University 淮北师范大学 http://chnu.admissions.cn Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities 16. Huangshan University 黄山学院 http://hsu.admissions.cn 17. Western Anhui University 皖西学院 http://wxc.admissions.cn 18. Chuzhou University 滁州学院 http://chzu.admissions.cn 19. Anhui University of Finance & Economics 安徽财经大学 http://aufe.admissions.cn 20. Suzhou University 宿州学院 http://ahszu.admissions.cn 21. -

University of Leeds Chinese Accepted Institution List 2021
University of Leeds Chinese accepted Institution List 2021 This list applies to courses in: All Engineering and Computing courses School of Mathematics School of Education School of Politics and International Studies School of Sociology and Social Policy GPA Requirements 2:1 = 75-85% 2:2 = 70-80% Please visit https://courses.leeds.ac.uk to find out which courses require a 2:1 and a 2:2. Please note: This document is to be used as a guide only. Final decisions will be made by the University of Leeds admissions teams. -

Current Knowledge of Bermudagrass Responses to Abiotic Stresses
Breeding Science Preview This article is an Advance Online Publication of the authors’ corrected proof. doi:10.1270/jsbbs.18164 Note that minor changes may be made before final version publication. Review Current knowledge of bermudagrass responses to abiotic stresses Shilian Huang†1), Shaofeng Jiang†2), Junsong Liang3), Miao Chen*4) and Yancai Shi5) 1) College of Life Sciences, South China Agricultural University, 483 Wushan Road, Guangzhou, Guangdong, 510642, China 2) Key Laboratory of Tumor Immunology and Microenvironmental Regulation, Guilin Medical University, 109 Huan Cheng North 2nd Road, Guilin, Guangxi, 541004, China 3) College of Biology & Pharmacy, Yulin Normal University, 1303 Jiaoyudong Road, Yulin, Guangxi, 537000, China 4) Faculty of Agricultural Science, Guangdong Ocean University, Haida Road #1, Zhanjiang, Guangdong, 524088, China 5) Guangxi Institute of Botany, Chinese Academy of Sciences, 85 Yanshan Town, Guilin, Guangxi, 541006, China Bermudagrass (Cynodon spp.) is a common turfgrass found in parks, landscapes, sports fields, and golf courses. It is also grown as a forage crop for animal production in many countries. Consequently, bermudagrass has significant ecological, environmental, and economic importance. Like many other food crops, bermudagrass production also faces challenges from various abiotic and biotic stresses. In this review we will focus on abiotic stresses and their impacts on turfgrass quality and yield. Among the abiotic stresses, drought, salinity and cold stress are known to be the most damaging stresses that can directly affect the production of turfgrass world- wide. In this review, we also discuss the impacts of nutrient supply, cadmium, waterlogging, shade and wear stresses on bermudagrass growth and development. Detailed discussions on abiotic stress effects on bermuda- grass morphology, physiology, and gene expressions should benefit our current understanding on molecular mechanisms controlling bermudagrass tolerance against various abiotic stresses. -
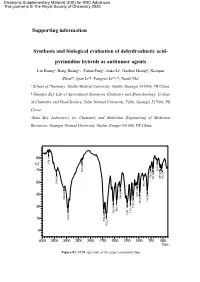
Supporting Information Synthesis and Biological Evaluation Of
Electronic Supplementary Material (ESI) for RSC Advances. This journal is © The Royal Society of Chemistry 2020 Supporting information Synthesis and biological evaluation of dehydroabietic acid- pyrimidine hybrids as antitumor agents Lin Huanga, Rong Huanga,Fuhua Panga, Anke Lia, Guobao Huangb, Xiaoqun Zhoua*, Qian Lia*, Fangyao Lia,b,c*, Xianli Maa a School of Pharmacy, Guilin Medical University, Guilin, Guangxi 541004, PR China b Guangxi Key Lab of Agricultural Resources Chemistry and Biotechnology, College of Chemistry and Food Science, Yulin Normal University, Yulin, Guangxi 537000, PR China cState Key Laboratory for Chemistry and Molecular Engineering of Medicinal Resources, Guangxi Normal University, Guilin, Gungxi 541006, PR China. 2 1 90 . 6 3 7 3 8 %T 4 0 9 . 1 8 2 5 6 75 3 2 0 3 7 1 8 4 . 5 . 8 . 6 . 7 6 5 7 5 0 2 7 0 5 0 5 . 7 4 4 1 5 4 . 60 3 6 0 9 0 7 . 1 9 7 6 8 3 . 0 9 4 45 3 1 9 8 5 4 . 0 3 8 5 3 1 . 2 9 1 8 7 7 . 9 8 1 1 2 1 1 5 . 7 1 5 . 30 6 0 . 2 1 6 9 . 7 4 2 2 1 1 5 4 1 7 1 2 8 1 6 . 3 9 . 2 4 9 8 2 15 2 2 7 . 1 2 7 6 1 0 4000 3500 3000 2500 2000 1750 1500 1250 1000 750 500 1/cm Figure S1. FTIR spectrum of the target compound (3a) 8 . -

Acknowledgments to Reviewers of Zoological Research
ZOOLOGICAL RESEARCH Acknowledgments to reviewers of Zoological Research The editors of Zoological Research gratefully acknowledge the generous assistance of the following reviewers. We are thankful for the honest and invaluable work of all the referees during the past year, which has greatly contributed to ensuring the quality of Zoological Research. Michael Braby Fang Zhou Australian National University, Australia Guangxi University, China Robert E. Schmidt Wei Liang Bard College at Simon's Rock, USA Hainan Normal University, China Yan-Yun Zhang Jie Mei Beijing Normal University, China Huazhong Agricultural University, China Joshua M. Hallas Lu-Bin Jiang Jian-Hua Wang Chi-Yu Zhang California Academy of Sciences, USA Institut Pasteur of Shanghai, Chinese Academy of Sciences, China Li Ding Jia-Tang Li Xiao-Mao Zeng Chengdu Institute of Biology, Chinese Academy of Sciences, Ke-Xin LI China Institute of Evolution, University of Haifa, Israel Lei Yang Huan-Zhang Liu Qiong-Ying Tang College of Charleston, USA Institute of Hydrobiology, Chinese Academy of Sciences, China Dai-Bin Zhong Qiang Wei College of Health Sciences, University of California, Irvine, USA Institute of Laboratory Animal Sciences, Chinese Academy of Medical Sciences, China Yun-Ke Wu Cornell University, USA Xin-Zheng Li Jing Liu Feng You Institute of Oceanology, Chinese Academy of Sciences, China Gerhard F. Weinbauer Covance Laboratories GmbH, Muenster, Germany Yong-Hui Li Institute of Psychology, Chinese Academy of Sciences, China Peng-Fei Fan Dali University, China Qin-Qin Shi Institute of Vertebrate Paleontology and Paleoanthropology, Fan Li Chinese Academy of Sciences, China Fudan University, China Qing-Sheng Chi Wei Guo Yi-Bo Hu Xin-Hai Li Xuan Liu Harriet L. -

MMTC Communications – Frontiers
IEEE COMSOC MMTC Communications – Frontiers MULTIMEDIA COMMUNICATIONS TECHNICAL COMMITTEE http://www.comsoc.org/~mmc MMTC Communications - Frontiers Vol. 13, No. 4, July 2018 CONTENTS Message from the MMTC Chair ......................................................................................3 SPECIAL ISSUE ON Terahertz Communication ..........................................................4 Guest Editor: Tuncer Baykas ........................................................................................4 Istanbul Medipol Univeristy, Turkey .............................................................................4 [email protected] ................................................................................................4 Propagation Channels in Terahertz Band .......................................................................5 Ali Rıza Ekti1, Serhan Yarkan2, Ali Görçin1, Murat Uysal3...........................................5 1TÜBİTAK BİLGEM, Turkey ,2Istanbul Commerce University, Turkey, 3Özyeğin University, Turkey ........................................................................................................5 [email protected] .............................................................................................5 On Some Issues Related to Statistical Modeling of Propagation Channels for Terahertz Band ..................................................................................................................9 Emre Ulusoy1, Özgür Alaca2, Gamze Kirman2, Ali Rıza Ekti1, Ali Görçin1 -

Research on Effect of Beijing Post-Olympic Sports Industry to China’S Economic Development
Available online at www.sciencedirect.com Energy Procedia 5 (2011) 2097–2102 IACEED2010 Research on Effect of Beijing Post-Olympic Sports Industry to China’s Economic Development Liuqian HUANG* Physical Education Department, Yulin Normal University, Yulin, 537000, China Abstract Research Methods: Using the literature information, discuss research on effect of Beijing post-Olympic sports industry to China’s economic development on basis of analyzing the impacts of Olympic Games on host country ’s economic development, from the angle of the theory of Olympic economic development. Purpose of research: Hope to offer theoretical basis for reference to China’s post-Olympic economic development through the research on the impacts of Olympic Games on host country’s economic development. Conclusions: Main industries that Beijing post - Olympic will promote development of China economic are: Sporting Goods Industry, Sports Tourism Industry, Leisure Sports Industry, and the standard of sports consumption and so on. Research Results: Beijing post -Olympic contributes to promote the formation and development of sports industry chain, “Olympic economy” that formed by sports industry will have an important role in promoting China’s economic development. © 2011 Published by Elsevier Ltd. Selection and peer-review under responsibility of RIUDS Key words: Post-Olympic; Sports Industry; China; Beijing 1. Impacts of Olympic Games on host country’s economic development The Olympic Games is the world’s most influential sports event, it will not only promote development of cultural and sporting goods and services industries, but also promote the economic growth of host city, stimulate regional economic development, and bring significant impact on host country’s economic. -

Table of Contents
2019 15th International Conference on Computational Intelligence and Security (CIS) CIS 2019 Table of Contents Preface xv Organizing Committee xvi Program Committee xvii Reviewers xviii Regular Papers Intelligent Algorithms Interactive Ontology Matching Based on Evolutionary Algorithm 1 Xingsi Xue (Fujian University of Technology), Junfeng Chen (Hohai University), and Aihong Ren (Baoji University of Arts and Sciences) An Image Segmentation Method Based on a Constrained Convex Variant of the Mumford-Shah Model 6 Zhanjiang Zhi (Henan University) and Shuaijie Li (Henan University of Science and Technology) RGB-D Object Tracking with Occlusion Detection 11 Yujun Xie (Beijing Institute of Technology), Yao Lu (Beijing Institute of Technology), and Shuang Gu (Beijing Institute of Technology) Application of the Faster R-CNN Algorithm in Scene Recognition Function Design 16 Li Xinyu (Guilin University of Electronic Technology), Lei Xiaochun (Guilin University of Electronic Technology), Chen Rongfeng (Guilin University of Electronic Technology), Feng Yizhou (Guilin University of Electronic Technology), Xiong Tianmin (Guilin University of Electronic Technology), and Chen Junyan (Guilin University of Electronic Technology) Infrared and Visible Image Fusion Based on Adaptive Dual-Channel PCNN and Saliency Detection 20 Ying An (Northwest University), Xunli Fan (Northwest University), Li Chen (Northwest University), and Pei Liu (Northwest University) High-Order Unscented Transformation Based on the Bayesian Learning for Nonlinear Systems with Non-Gaussian -
1 Please Read These Instructions Carefully
PLEASE READ THESE INSTRUCTIONS CAREFULLY. MISTAKES IN YOUR CSC APPLICATION COULD LEAD TO YOUR APPLICATION BEING REJECTED. Visit http://studyinchina.csc.edu.cn/#/login to CREATE AN ACCOUNT. • The online application works best with Firefox or Internet Explorer (11.0). Menu selection functions may not work with other browsers. • The online application is only available in Chinese and English. 1 • Please read this page carefully before clicking on the “Application online” tab to start your application. 2 • The Program Category is Type B. • The Agency No. matches the university you will be attending. See Appendix A for a list of the Chinese university agency numbers. • Use the + by each section to expand on that section of the form. 3 • Fill out your personal information accurately. o Make sure to have a valid passport at the time of your application. o Use the name and date of birth that are on your passport. Use the name on your passport for all correspondences with the CLIC office or Chinese institutions. o List Canadian as your Nationality, even if you have dual citizenship. Only Canadian citizens are eligible for CLIC support. o Enter the mailing address for where you want your admission documents to be sent under Permanent Address. Leave Current Address blank. Contact your home or host university coordinator to find out when you will receive your admission documents. Contact information for you home university CLIC liaison can be found here: http://clicstudyinchina.com/contact-us/ 4 • Fill out your Education and Employment History accurately. o For Highest Education enter your current degree studies. -

Research Article Construction of the Teaching Quality Monitoring
Hindawi Mathematical Problems in Engineering Volume 2021, Article ID 9907531, 11 pages https://doi.org/10.1155/2021/9907531 Research Article Construction of the Teaching Quality Monitoring System of Physical Education Courses in Colleges and Universities Based on the Construction of Smart Campus with Artificial Intelligence Xiang Huang,1 Xingyu Huang,2 and Xiaoping Wang 3 1School of Physical Education and Health, Yulin Normal University, Yulin, Guangxi 537000, China 2School of Electronic Information, Guangxi University for Nationalities, Nanning, Guangxi 530006, China 3School of Biology and Pharmacy, Yulin Normal University, Yulin, Guangxi 537000, China Correspondence should be addressed to Xiaoping Wang; [email protected] Received 13 July 2021; Revised 12 August 2021; Accepted 23 August 2021; Published 29 August 2021 Academic Editor: Sang-Bing Tsai Copyright © 2021 Xiang Huang et al. +is is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. With regard to the development of colleges and universities, ensuring the quality of education is the fundamental goal and main task of teaching daily management. With the continuous improvement of the application level of the Internet and other in- formation technologies, the construction of smart campus in colleges and universities in China is rapidly advancing. +is paper studies the construction and innovation strategy of the public sports quality monitoring system and discusses the changes in college students’ sports quality after the introduction of smart campuses from the perspective of artificial intelligence and the creation of smart universities. In this paper, the field survey method and other research methods are combined to study, and in the process of data storage, SQL Server database platform is used to store the data. -

FORMATO PDF Ranking Instituciones Acadã©Micas Por Sub áRea OCDE
Ranking Instituciones Académicas por sub área OCDE 2020 1. Cs. Naturales > 1.02 Computación y Ciencias de la Informática PAÍS INSTITUCIÓN RANKING PUNTAJE CHINA Tsinghua University 1 5,000 USA Carnegie Mellon University 2 5,000 USA University of California Berkeley 3 5,000 USA Stanford University 4 5,000 USA Massachusetts Institute of Technology (MIT) 5 5,000 SINGAPORE Nanyang Technological University & National Institute of Education (NIE) Singapore 6 5,000 SWITZERLAND ETH Zurich 7 5,000 USA University of Michigan 8 5,000 HONG KONG Chinese University of Hong Kong 9 5,000 SINGAPORE National University of Singapore 10 5,000 CHINA Shanghai Jiao Tong University 11 5,000 FRANCE Universite Cote d'Azur (ComUE) 12 5,000 UNITED KINGDOM University of Oxford 13 5,000 USA University of Illinois Urbana-Champaign 14 5,000 CHINA Harbin Institute of Technology 15 5,000 CHINA Peking University 16 5,000 USA University of Washington Seattle 17 5,000 USA Georgia Institute of Technology 18 5,000 AUSTRALIA University of Technology Sydney 19 5,000 GERMANY Technical University of Munich 20 5,000 CHINA University of Science & Technology of China 21 5,000 UNITED KINGDOM University College London 22 5,000 USA Cornell University 23 5,000 UNITED KINGDOM Imperial College London 24 5,000 CHINA University of Electronic Science & Technology of China 25 5,000 USA University of North Carolina Chapel Hill 26 5,000 CHINA Beihang University 27 5,000 CHINA Zhejiang University 28 5,000 CHINA Huazhong University of Science & Technology 29 5,000 USA University of Southern California -

Satellite Salon Program
~ Upcoming Events ~ Honor Orchestra September 18 • 4:00p Heritage Center - Ticketed Event Alumni Band Concert/Virginia Stitt Tribute September 24 • 7:00p Heritage Center - Ticketed Event CAN-AM Trio Guest Artists September 28 • 12:00pm Thorley Recital Hall - FREE Choir Concert (Masterworks) October 1 • 7:30p Heritage Center – Ticketed Event Piano Monster Concert October 26 • 7:00p Heritage Center – Ticketed Event Wind Symphony Concert (Masterworks) November 5 • 7:30p Heritage Center – Ticketed Event Opera November 10 • 7:30p Thorley Recital Hall - FREE Brass and Woodwind Ensembles November 15 • 7:30p Thorley Recital Hall - FREE Dr. Laura Grantier Program Dr. Laura D. Grantier, a native of Denham Springs, LA, earned a Bachelor of Music from the University of Alabama in 1993, an MBA from Averett University in 2003, Yeni Makam Edward J Hines and a Doctor of Musical Arts from the Catholic University of America in 2012. Her teachers are Scott Bridges, Ken Grant, and Eugene Mondie. I. “Taksim” (b. 1951) II. “Bir Karpuzmus” Dr. Grantier joined SUU as Director of Woodwinds and Assistant Professor of Clarinet III. “Harem Havasi” at Southern Utah University in August 2021. From 1995-2021 she was a member of IV. “Dan Dun Davulu” the United States Navy Band in Washington, D.C. where she served as Principal Clarinet, Woodwind Leader, Clarinet Section Leader, and Harborwinds Clarinet Quartet Leader. She performed over 2,250 public concerts, military ceremonies, Prelude to a Dream Bryce Craig education workshops, and high-profile protocol engagements for high-ranking (b. 1990) dignitaries, including the President of the United States, Vice President of the United States, and Secretary of the Navy.