Math 103 Finite Math with a Special Emphasis on Math & Art 2
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1-Crystal Symmetry and Classification-1.Pdf
R. I. Badran Solid State Physics Fundamental types of lattices and crystal symmetry Crystal symmetry: What is a symmetry operation? It is a physical operation that changes the positions of the lattice points at exactly the same places after and before the operation. In other words, it is an operation when applied to an object leaves it apparently unchanged. e.g. A translational symmetry is occurred, for example, when the function sin x has a translation through an interval x = 2 leaves it apparently unchanged. Otherwise a non-symmetric operation can be foreseen by the rotation of a rectangle through /2. There are two groups of symmetry operations represented by: a) The point groups. b) The space groups (these are a combination of point groups with translation symmetry elements). There are 230 space groups exhibited by crystals. a) When the symmetry operations in crystal lattice are applied about a lattice point, the point groups must be used. b) When the symmetry operations are performed about a point or a line in addition to symmetry operations performed by translations, these are called space group symmetry operations. Types of symmetry operations: There are five types of symmetry operations and their corresponding elements. 85 R. I. Badran Solid State Physics Note: The operation and its corresponding element are denoted by the same symbol. 1) The identity E: It consists of doing nothing. 2) Rotation Cn: It is the rotation about an axis of symmetry (which is called "element"). If the rotation through 2/n (where n is integer), and the lattice remains unchanged by this rotation, then it has an n-fold axis. -
![Arxiv:1910.10745V1 [Cond-Mat.Str-El] 23 Oct 2019 2.2 Symmetry-Protected Time Crystals](https://docslib.b-cdn.net/cover/4942/arxiv-1910-10745v1-cond-mat-str-el-23-oct-2019-2-2-symmetry-protected-time-crystals-304942.webp)
Arxiv:1910.10745V1 [Cond-Mat.Str-El] 23 Oct 2019 2.2 Symmetry-Protected Time Crystals
A Brief History of Time Crystals Vedika Khemania,b,∗, Roderich Moessnerc, S. L. Sondhid aDepartment of Physics, Harvard University, Cambridge, Massachusetts 02138, USA bDepartment of Physics, Stanford University, Stanford, California 94305, USA cMax-Planck-Institut f¨urPhysik komplexer Systeme, 01187 Dresden, Germany dDepartment of Physics, Princeton University, Princeton, New Jersey 08544, USA Abstract The idea of breaking time-translation symmetry has fascinated humanity at least since ancient proposals of the per- petuum mobile. Unlike the breaking of other symmetries, such as spatial translation in a crystal or spin rotation in a magnet, time translation symmetry breaking (TTSB) has been tantalisingly elusive. We review this history up to recent developments which have shown that discrete TTSB does takes place in periodically driven (Floquet) systems in the presence of many-body localization (MBL). Such Floquet time-crystals represent a new paradigm in quantum statistical mechanics — that of an intrinsically out-of-equilibrium many-body phase of matter with no equilibrium counterpart. We include a compendium of the necessary background on the statistical mechanics of phase structure in many- body systems, before specializing to a detailed discussion of the nature, and diagnostics, of TTSB. In particular, we provide precise definitions that formalize the notion of a time-crystal as a stable, macroscopic, conservative clock — explaining both the need for a many-body system in the infinite volume limit, and for a lack of net energy absorption or dissipation. Our discussion emphasizes that TTSB in a time-crystal is accompanied by the breaking of a spatial symmetry — so that time-crystals exhibit a novel form of spatiotemporal order. -

Translational Symmetry and Microscopic Constraints on Symmetry-Enriched Topological Phases: a View from the Surface
PHYSICAL REVIEW X 6, 041068 (2016) Translational Symmetry and Microscopic Constraints on Symmetry-Enriched Topological Phases: A View from the Surface Meng Cheng,1 Michael Zaletel,1 Maissam Barkeshli,1 Ashvin Vishwanath,2 and Parsa Bonderson1 1Station Q, Microsoft Research, Santa Barbara, California 93106-6105, USA 2Department of Physics, University of California, Berkeley, California 94720, USA (Received 15 August 2016; revised manuscript received 26 November 2016; published 29 December 2016) The Lieb-Schultz-Mattis theorem and its higher-dimensional generalizations by Oshikawa and Hastings require that translationally invariant 2D spin systems with a half-integer spin per unit cell must either have a continuum of low energy excitations, spontaneously break some symmetries, or exhibit topological order with anyonic excitations. We establish a connection between these constraints and a remarkably similar set of constraints at the surface of a 3D interacting topological insulator. This, combined with recent work on symmetry-enriched topological phases with on-site unitary symmetries, enables us to develop a framework for understanding the structure of symmetry-enriched topological phases with both translational and on-site unitary symmetries, including the effective theory of symmetry defects. This framework places stringent constraints on the possible types of symmetry fractionalization that can occur in 2D systems whose unit cell contains fractional spin, fractional charge, or a projective representation of the symmetry group. As a concrete application, we determine when a topological phase must possess a “spinon” excitation, even in cases when spin rotational invariance is broken down to a discrete subgroup by the crystal structure. We also describe the phenomena of “anyonic spin-orbit coupling,” which may arise from the interplay of translational and on-site symmetries. -

About Symmetries in Physics
LYCEN 9754 December 1997 ABOUT SYMMETRIES IN PHYSICS Dedicated to H. Reeh and R. Stora1 Fran¸cois Gieres Institut de Physique Nucl´eaire de Lyon, IN2P3/CNRS, Universit´eClaude Bernard 43, boulevard du 11 novembre 1918, F - 69622 - Villeurbanne CEDEX Abstract. The goal of this introduction to symmetries is to present some general ideas, to outline the fundamental concepts and results of the subject and to situate a bit the following arXiv:hep-th/9712154v1 16 Dec 1997 lectures of this school. [These notes represent the write-up of a lecture presented at the fifth S´eminaire Rhodanien de Physique “Sur les Sym´etries en Physique” held at Dolomieu (France), 17-21 March 1997. Up to the appendix and the graphics, it is to be published in Symmetries in Physics, F. Gieres, M. Kibler, C. Lucchesi and O. Piguet, eds. (Editions Fronti`eres, 1998).] 1I wish to dedicate these notes to my diploma and Ph.D. supervisors H. Reeh and R. Stora who devoted a major part of their scientific work to the understanding, description and explo- ration of symmetries in physics. Contents 1 Introduction ................................................... .......1 2 Symmetries of geometric objects ...................................2 3 Symmetries of the laws of nature ..................................5 1 Geometric (space-time) symmetries .............................6 2 Internal symmetries .............................................10 3 From global to local symmetries ...............................11 4 Combining geometric and internal symmetries ...............14 -
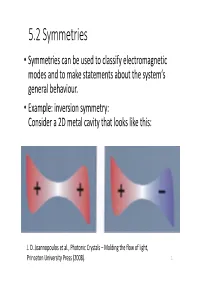
5.2 Symmetries • Symmetries Can Be Used to Classify Electromagnetic Modes and to Make Statements About the System‘S General Behaviour
5.2 Symmetries • Symmetries can be used to classify electromagnetic modes and to make statements about the system‘s general behaviour. • Example: inversion symmetry: Consider a 2D metal cavity that looks like this: J. D. Joannopoulos et al., Photonic Crystals – Molding the flow of light, Princeton University Press (2008). 1 • The shape is somewhat arbitrary, making an analytical solution difficult, but it has inversion symmetry if is a mode with frequency , then must also be a mode with frequency • Unless is a member of a degenerate family of modes, then if has the same frequency, it must be the same mode, i.e. it must be a multiple of : . • If we invert the system twice we obtain or . • A given nondegenerate mode must be of one of the two types, either it is invariant under inversion (even mode) or it becomes its own opposite (odd mode). • Thereby we have classified the modes of the system based on how they respond to one of its symmetry operations. 2 • Let‘s capture this idea in a more abstract language • Suppose is an operator (a 3x3 matrix) that inverts vectors (3x1 matrices), so that • To invert a vector field, we need an operator that inverts both the vector and ist argument : • For an inversion symmetric system it does not matter if we operate with or if we first invert the coordinates, then operate with , and then change them back, i.e.: (73) • This equation can be rearranged: =0 • We can define the commutator (74) which is itself an operator 3 • For our inversion symmetric example system we have ,Θ 0. -

Translational Spacetime Symmetries in Gravitational Theories
Class. Quantum Grav. 23 (2006) 737-751 Page 1 Translational Spacetime Symmetries in Gravitational Theories R. J. Petti The MathWorks, Inc., 3 Apple Hill Drive, Natick, MA 01760, U.S.A. E-mail: [email protected] Received 24 October 2005, in final form 25 October 2005 Published DD MM 2006 Online ta stacks.iop.org/CQG/23/1 Abstract How to include spacetime translations in fibre bundle gauge theories has been a subject of controversy, because spacetime symmetries are not internal symmetries of the bundle structure group. The standard method for including affine symmetry in differential geometry is to define a Cartan connection on an affine bundle over spacetime. This is equivalent to (1) defining an affine connection on the affine bundle, (2) defining a zero section on the associated affine vector bundle, and (3) using the affine connection and the zero section to define an ‘associated solder form,’ whose lift to a tensorial form on the frame bundle becomes the solder form. The zero section reduces the affine bundle to a linear bundle and splits the affine connection into translational and homogeneous parts; however it violates translational equivariance / gauge symmetry. This is the natural geometric framework for Einstein-Cartan theory as an affine theory of gravitation. The last section discusses some alternative approaches that claim to preserve translational gauge symmetry. PACS numbers: 02.40.Hw, 04.20.Fy 1. Introduction Since the beginning of the twentieth century, much of the foundations of physics has been interpreted in terms of the geometry of connections and curvature. Connections appear in three main areas. -

Effective Field Theory for Spacetime Symmetry Breaking
RIKEN-MP-96, RIKEN-QHP-171, MAD-TH-14-10 Effective field theory for spacetime symmetry breaking Yoshimasa Hidaka1, Toshifumi Noumi1 and Gary Shiu2;3 1Theoretical Research Devision, RIKEN Nishina Center, Japan 2Department of Physics, University of Wisconsin, Madison, WI 53706, USA 3Center for Fundamental Physics and Institute for Advanced Study, Hong Kong University of Science and Technology, Hong Kong [email protected], [email protected], [email protected] Abstract We discuss the effective field theory for spacetime symmetry breaking from the local symmetry point of view. By gauging spacetime symmetries, the identification of Nambu-Goldstone (NG) fields and the construction of the effective action are performed based on the breaking pattern of diffeomor- phism, local Lorentz, and (an)isotropic Weyl symmetries as well as the internal symmetries including possible central extensions in nonrelativistic systems. Such a local picture distinguishes, e.g., whether the symmetry breaking condensations have spins and provides a correct identification of the physical NG fields, while the standard coset construction based on global symmetry breaking does not. We illustrate that the local picture becomes important in particular when we take into account massive modes associated with symmetry breaking, whose masses are not necessarily high. We also revisit the coset construction for spacetime symmetry breaking. Based on the relation between the Maurer- arXiv:1412.5601v2 [hep-th] 7 Nov 2015 Cartan one form and connections for spacetime symmetries, we classify the physical meanings of the inverse Higgs constraints by the coordinate dimension of broken symmetries. Inverse Higgs constraints for spacetime symmetries with a higher dimension remove the redundant NG fields, whereas those for dimensionless symmetries can be further classified by the local symmetry breaking pattern. -

Diffeomorphisms and Spin Foam Models
Diffeomorphisms and spin foam models Laurent Freidel∗ Perimeter Institute for Theoretical Physics 35 King street North, Waterloo N2J-2G9,Ontario, Canada and Laboratoire de Physique, Ecole´ Normale Sup´erieure de Lyon 46 all´ee d’Italie, 69364 Lyon Cedex 07, France David Louapre† Laboratoire de Physique, Ecole´ Normale Sup´erieure de Lyon 46 all´ee d’Italie, 69364 Lyon Cedex 07, France‡ (Dated: February 7, 2008) Abstract We study the action of diffeomorphisms on spin foam models. We prove that in 3 dimensions, there is a residual action of the diffeomorphisms that explains the naive divergences of state sum models. We present the gauge fixing of this symmetry and show that it explains the original renormalization of Ponzano-Regge model. We discuss the implication this action of diffeomorphisms has on higher dimensional spin foam models and especially the finite ones. arXiv:gr-qc/0212001v2 29 Jan 2003 ∗Electronic address: [email protected] †Electronic address: [email protected] ‡UMR 5672 du CNRS 0 I. INTRODUCTION Spin foam models are an attempt to describe the geometry of spacetime at the quantum level. They give a construction of transition amplitudes between initial and final spatial geometries labeled by spin network states. A spin foam is a 2-dimensional cell complex F with polygonal faces labeled by representations jf and edges labeled by intertwining operators ie. Given a spin foam we associate an amplitude Af , Ae and Av to the faces, edges and vertices of the spin foam respectively. They depend only locally on the spins jf and intertwiners ıe, e-g the vertex amplitude is computed using the spins labeling the faces incident to that vertex and intertwiners on incident edges. -

Translational Symmetry. Rotational Symmetry
Physics and Material Science of Semiconductor Nanostructures PHYS 570P Prof. Oana Malis Email: [email protected] Course website: http://www.physics.purdue.edu/academic_programs/courses/phys570P/ Lecture Review of quantum mechanics, statistical physics, and solid state Band structure of materials Semiconductor band structure Semiconductor nanostructures Ref. Ihn Ch. 3, Yu&Cardona Ch. 2 The Bandstructure Problem • Begin with the one‐electron Hamiltonian: 2 H1e = (p) /(2mo) + V(r) p ‐iħ, V(r) Periodic Effective Potential • Solve the one‐electron Schrödinger Equation: H1eψn(r) = Enψn(r) In general, this is still a very complex, highly computational problem! The Bandstructure Problem (Many people’s careers over many years!) • Start with the 1 e‐ Hamiltonian: 2 H1e = ‐(iħ) /(2mo) + V(r) • Step 1: Determine the effective periodic potential V(r) • Step 2: Solve the one‐electron Schrödinger Equation: H1eψn(r) = Enψn(r) A complex, sophisticated, highly computational problem! • There are many schemes, methods, & theories to do this! • We’ll give a brief overview of only a few. • The 1 e‐ Hamiltonian is: 2 H1e = ‐(iħ) /(2mo) + V(r) NOTE Knowing the exact form of the effective periodic potential V(r) is itself a difficult problem! • However, we can go a long way towards understanding the physics behind the nature of bandstructures without specifying V(r). We can USE SYMMETRY. Group Theory A math tool which does this in detail. V(r) Periodic Crystal Potential. It has all of the symmetries of the crystal lattice. Translational symmetry. Rotational symmetry. Reflection symmetry • The most important symmetry is Translational Symmetry. • Using this considerably reduces the complexities of bandstructure calculations. -

1 General Impact of Translational Symmetry in Crystals on Solid State Physics
1 1 General Impact of Translational Symmetry in Crystals on Solid State Physics Atomic order in crystals. Local and translational symmetries. Symmetry impact on physical properties in crystals. Wave propagation in periodic media. Quasi-momentum conservation law. Reciprocal space. Wave diffraction conditions. Degeneracy of electron energy states at the Brillouin zone boundary. Diffraction of valence electrons and bandgap formation. In contrast to liquids or gases, atoms in a solid state, in average (over time), are located at fixed atomic positions. The thermally assisted movements around them or between them are strongly limited in space (as for thermal vibrations in potential wells) or have rather low probabilities (as for long-range atomic diffusion). Accord- ing to the types of the averaged long-range atomic arrangements, all solid materials can be sub-divided into the three following classes, i.e. regular crystals, amorphous materials, and quasicrystals. Most solid materials are regular (conventional) crystals with fully ordered and periodic atomic arrangements, which can be described by the set of translated elementary blocks (unit cells) densely covering the space with no voids. Nowadays, using the advanced characterization methods, such as high-resolution electron microscopy or scanning tunneling microscopy, it is possible to directly visualize this atomic periodicity (Figure 1.1). Due to the translational symmetry, the key phenomenon – namely, diffraction of short-wavelength quantum beams (electrons, X-rays, neutrons) – takes place. As we show in the following text, sharp diffraction peaks (or spots), which are the “visiting card” of crystalline state, are originated from the quasi-momentum (quasi-wavevector) conservation law in 3D. In contrary, amorphous materials, being characterized by some kind of short- range ordering, do not reveal atomic order on a long range (Figure 1.2). -

On One-Dimensional Crystals Earlier, We Saw Earlier That the Characters for the N Irreducible Representations Of
More on One-Dimensional Crystals Earlier, we saw earlier that the characters for the N irreducible representations of the one-dimensional translation group (TN) can be written as tt2 t3 tN1 tN = E 2 i(k•a) 2 i(k•2a) 2 i(k•3a) 2 i(k•a) (k) e e e e 1 Where k takes on exactly N discrete values within the range -1 (2a) < k 1(2a) and a is the unit cell length. This compressed “table” tells us all we need to know to discuss functions that form a basis for any of the irreducible representations of the TN group. For example, we know that if we operate on a function k that forms a basis for the irreducible representation (k) with the translation operator t , the result can be read directly from the character table: 2i(ka) tk = e k . m More generally, if we operate on k with any of the translation operators t , we obtain m 2i(kma) t k = e k . It is also useful to note that the representation (-k) (with a corresponding basis function k ) yields eigenvalues that are just the complex conjugates 2i(ka) m 2i(kma) tk = e k and t k = e k , where e2i(ka) = (e2i(k a) )* and e2i(kma) = (e2i(kma))* . But, because the operator t simply shifts the chain by one unit cell length (a ) along the x -axis, this means that as functions that belong to the (k) and (-k) representations, k and k have the important properties: 2i(k a) 2i(ka ) k (x + a) = e k (x) and k (x + a) = e k (x) . -

Lectures on “Introduction to the Group Theory” (I. Eremin, MPIPKS Dresden and TU Braunschweig)
Lectures on “Introduction to the Group Theory” (I. Eremin, MPIPKS Dresden and TU Braunschweig) Lecture1 (21.04.2006) Abstract Group Theory • What is a Group? • The Multiplication Table, Conjugate Eelements and Classes • Subgroups • The Direct Product of Groups • Homomorphism, Permutation Groups Lecture 2* (24.04.2006) Hilbert Spaces and Operators • Vector Spaces and Hilbert Spaces • Coordinate Geometry and Vector Algebra in a New Notation • Operators • Unitary Operators and Unitary Matrices Lecture 3 (26.04.2006) Representation of a Group I • Invariant Subspaces and Reducible Representations • The Schur’s Lemmas and OrthogonalityTheorem • The Characters of a Representation • The example of C4v Lecture 4 (28.04.2006) Representation of a Group II • The Regular Representation • Other Reducible Representations • The Direct Product of Reprsentations Lecture 5 (03.05.2006) Continuous Groups • Topological Groups and Lie Groups • The Axial Rotation Group O(2) • The three-dimensional Rotation Group O(3) • The Special Unitary Group SU(2) • Lie Algebra and Representations of a Lie Group Lecture 6 (05.05.2006) Group Theory in Quantum Mechanics I • Hilbert Spaces in Quantum Mechanics • Space and Time Displacements • Symmetry of the Hamiltonian • Reduction due to Symmetry Lecture 7* (08.05.2006) Group Theory in Quantum Mechanics II • Perturbation and Level Splitting • The Matrix Element Theorem and Selection Rules • Dynamical Symmetry • Time Reversal and Space Inversion Symmetries Lecture 8 (10.05.2006) Group Theory in Quantum Mechanics III • Atomic