2D Transformations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Projective Geometry: a Short Introduction
Projective Geometry: A Short Introduction Lecture Notes Edmond Boyer Master MOSIG Introduction to Projective Geometry Contents 1 Introduction 2 1.1 Objective . .2 1.2 Historical Background . .3 1.3 Bibliography . .4 2 Projective Spaces 5 2.1 Definitions . .5 2.2 Properties . .8 2.3 The hyperplane at infinity . 12 3 The projective line 13 3.1 Introduction . 13 3.2 Projective transformation of P1 ................... 14 3.3 The cross-ratio . 14 4 The projective plane 17 4.1 Points and lines . 17 4.2 Line at infinity . 18 4.3 Homographies . 19 4.4 Conics . 20 4.5 Affine transformations . 22 4.6 Euclidean transformations . 22 4.7 Particular transformations . 24 4.8 Transformation hierarchy . 25 Grenoble Universities 1 Master MOSIG Introduction to Projective Geometry Chapter 1 Introduction 1.1 Objective The objective of this course is to give basic notions and intuitions on projective geometry. The interest of projective geometry arises in several visual comput- ing domains, in particular computer vision modelling and computer graphics. It provides a mathematical formalism to describe the geometry of cameras and the associated transformations, hence enabling the design of computational ap- proaches that manipulates 2D projections of 3D objects. In that respect, a fundamental aspect is the fact that objects at infinity can be represented and manipulated with projective geometry and this in contrast to the Euclidean geometry. This allows perspective deformations to be represented as projective transformations. Figure 1.1: Example of perspective deformation or 2D projective transforma- tion. Another argument is that Euclidean geometry is sometimes difficult to use in algorithms, with particular cases arising from non-generic situations (e.g. -

Lecture 12: Camera Projection
Robert Collins CSE486, Penn State Lecture 12: Camera Projection Reading: T&V Section 2.4 Robert Collins CSE486, Penn State Imaging Geometry W Object of Interest in World Coordinate System (U,V,W) V U Robert Collins CSE486, Penn State Imaging Geometry Camera Coordinate Y System (X,Y,Z). Z X • Z is optic axis f • Image plane located f units out along optic axis • f is called focal length Robert Collins CSE486, Penn State Imaging Geometry W Y y X Z x V U Forward Projection onto image plane. 3D (X,Y,Z) projected to 2D (x,y) Robert Collins CSE486, Penn State Imaging Geometry W Y y X Z x V u U v Our image gets digitized into pixel coordinates (u,v) Robert Collins CSE486, Penn State Imaging Geometry Camera Image (film) World Coordinates Coordinates CoordinatesW Y y X Z x V u U v Pixel Coordinates Robert Collins CSE486, Penn State Forward Projection World Camera Film Pixel Coords Coords Coords Coords U X x u V Y y v W Z We want a mathematical model to describe how 3D World points get projected into 2D Pixel coordinates. Our goal: describe this sequence of transformations by a big matrix equation! Robert Collins CSE486, Penn State Backward Projection World Camera Film Pixel Coords Coords Coords Coords U X x u V Y y v W Z Note, much of vision concerns trying to derive backward projection equations to recover 3D scene structure from images (via stereo or motion) But first, we have to understand forward projection… Robert Collins CSE486, Penn State Forward Projection World Camera Film Pixel Coords Coords Coords Coords U X x u V Y y v W Z 3D-to-2D Projection • perspective projection We will start here in the middle, since we’ve already talked about this when discussing stereo. -

Point Sets up to Rigid Transformations Are Determined by the Distribution of Their Pairwise Distances
Point Sets Up to Rigid Transformations are Determined by the Distribution of their Pairwise Distances Daniel Chen December 6, 2008 Abstract This report is a summary of [BK06], which gives a simpler, albeit less general proof for the result of [BK04]. 1 Introduction [BK04] and [BK06] study the circumstances when sets of n-points in Euclidean space are determined up to rigid transformations by the distribution of unlabeled pairwise distances. In fact, they show the rather surprising result that any set of n-points in general position are determined up to rigid transformations by the distribution of unlabeled distances. 1.1 Practical Motivation The results of [BK04] and [BK06] are partly motivated by experimental results in [OFCD]. [OFCD] is an experimental study evaluating the use of shape distri- butions to classify 3D objects represented by point clouds. A shape distribution is a the distribution of a function on a randomly selected set of points from the point cloud. [OFCD] tested various such functions, including the angle be- tween three random points on the surface, the distance between the centroid and a random point, the distance between two random points, the square root of the area of the triangle between three random points, and the cube root of the volume of the tetrahedron between four random points. Then, the distri- butions are compared using dissimilarity measures, including χ2, Battacharyya, and Minkowski LN norms for both the pdf and cdf for N = 1; 2; 1. The experimental results showed that the shape distribution function that worked best for classification was the distance between two random points and the best dissimilarity measure was the pdf L1 norm. -

Draft Framework for a Teaching Unit: Transformations
Co-funded by the European Union PRIMARY TEACHER EDUCATION (PrimTEd) PROJECT GEOMETRY AND MEASUREMENT WORKING GROUP DRAFT FRAMEWORK FOR A TEACHING UNIT Preamble The general aim of this teaching unit is to empower pre-service students by exposing them to geometry and measurement, and the relevant pe dagogical content that would allow them to become skilful and competent mathematics teachers. The depth and scope of the content often go beyond what is required by prescribed school curricula for the Intermediate Phase learners, but should allow pre- service teachers to be well equipped, and approach the teaching of Geometry and Measurement with confidence. Pre-service teachers should essentially be prepared for Intermediate Phase teaching according to the requirements set out in MRTEQ (Minimum Requirements for Teacher Education Qualifications, 2019). “MRTEQ provides a basis for the construction of core curricula Initial Teacher Education (ITE) as well as for Continuing Professional Development (CPD) Programmes that accredited institutions must use in order to develop programmes leading to teacher education qualifications.” [p6]. Competent learning… a mixture of Theoretical & Pure & Extrinsic & Potential & Competent learning represents the acquisition, integration & application of different types of knowledge. Each type implies the mastering of specific related skills Disciplinary Subject matter knowledge & specific specialized subject Pedagogical Knowledge of learners, learning, curriculum & general instructional & assessment strategies & specialized Learning in & from practice – the study of practice using Practical learning case studies, videos & lesson observations to theorize practice & form basis for learning in practice – authentic & simulated classroom environments, i.e. Work-integrated Fundamental Learning to converse in a second official language (LOTL), ability to use ICT & acquisition of academic literacies Knowledge of varied learning situations, contexts & Situational environments of education – classrooms, schools, communities, etc. -

Half-Turns and Line Symmetric Motions
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by LSBU Research Open Half-turns and Line Symmetric Motions J.M. Selig Faculty of Business, Computing and Info. Management, London South Bank University, London SE1 0AA, U.K. (e-mail: [email protected]) and M. Husty Institute of Basic Sciences in Engineering Unit Geometry and CAD, Leopold-Franzens-Universit¨at Innsbruck, Austria. (e-mail: [email protected]) Abstract A line symmetric motion is the motion obtained by reflecting a rigid body in the successive generator lines of a ruled surface. In this work we review the dual quaternion approach to rigid body displacements, in particular the representation of the group SE(3) by the Study quadric. Then some classical work on reflections in lines or half-turns is reviewed. Next two new characterisations of line symmetric motions are presented. These are used to study a number of examples one of which is a novel line symmetric motion given by a rational degree five curve in the Study quadric. The rest of the paper investigates the connection between sets of half-turns and linear subspaces of the Study quadric. Line symmetric motions produced by some degenerate ruled surfaces are shown to be restricted to certain 2-planes in the Study quadric. Reflections in the lines of a linear line complex lie in the intersection of a the Study-quadric with a 4-plane. 1 Introduction In this work we revisit the classical idea of half-turns using modern mathematical techniques. In particular we use the dual quaternion representation of rigid-body motions. -

Rigid Transformations
Mathematical Principles in Vision and Graphics: Rigid Transformations Ass.Prof. Friedrich Fraundorfer SS 2018 Learning goals . Understand the problems of dealing with rotations . Understand how to represent rotations . Understand the terms SO(3) etc. Understand the use of the tangent space . Understand Euler angles, Axis-Angle, and quaternions . Understand how to interpolate, filter and optimize rotations 2 Outline . Rigid transformations . Problems with rotation matrices . Properties of rotation matrices . Matrix groups SO(3), SE(3) . Manifolds . Tangent space . Skew-symmetric matrices . Exponential map . Euler angles, angle-axis, quaternions . Interpolation . Filtering . Optimization 3 Motivation: 3D Viewer Rigid transformations 푧 푝 푋퐶 푍 푋푤 푥 퐶 푦 푂 푊 푇 푅 푂 푌 푥 ∈ ℝ푛 푋 푋푐 = 푅푋푤 + 푇 T ∈ ℝ푛 . Coordinates are related by: 푋푐 푅 푇 푋푤 = 푛×푛 1 0 1 1 푅 ∈ ℝ . Rigid transformation belong to the matrix group SE(3) . What does this mean? 5 Properties of rotation matrices Rotation matrix: 푧 푍 3×3 푅 = 푟1, 푟2, 푟3 ∈ ℝ 푟3 푦 푟2 푇 푅 푅 = 퐼, det 푅 = +1 푂 푌 푟1 푋 푥 Coordinates are related by: 푋푐 = 푅푋푤 . Rotation matrices belong to the matrix group SO(3) . What does this mean? 6 Problems with rotation matrices . Optimization of rotations (bundle adjustment) 푓(푥푛) ▫ Newton’s method 푥푛+1 = 푥푛 − 푓′(푥푛) . Linear interpolation . Filtering and averaging ▫ E.g. averaging rotation from IMU or camera pose tracker for AR/VR glasses 7 Matrix groups . The set of all the nxn invertible matrices is a group w.r.t. the matrix multiplication: 퐺퐿(푛) = 푀 ∈ ℝ푛×푛|det(푀) ≠ 0 ,× General linear group . -

Unit 5 Transformations in the Coordinate Plane
Coordinate Algebra: Unit 5 Transformations in the Coordinate Plane Learning Targets: I can… Important Understandings and Concepts • Define angles, circles, perpendicular lines, parallel lines, rays, and line segments precisely using the undefined terms and “if- then” and “if-and-only-if” statements. • Draw transformations of reflections, rotations, translations, and combinations of these using graph paper, transparencies, and /or geometry software. Transformational geometry is about the effects of rigid motions, rotations, • Determine the coordinates for the image (output) of a figure reflections and translations on figures. A reflection is a flip over a line. when a transformation rule is applied to the preimage (input). Reflections have the same shape and size as the original image. • Calculate the number of lines of reflection symmetry and the degree of rotational symmetry of any regular polygon. • Draw a specific transformation when given a geometric figure and a rotation, reflection, or translation. • Predict and verify the sequence of transformations (a composition) that will map a figure onto another. Vocabulary angle – is the figure formed by two rays, called the sides of the angle, sharing a common endpoint. A translation or “slide” is moving a shape, without rotating or flipping it. rigid transformation: is one in which the pre-image and the image The shape still looks exactly the same, just in a different place. both have the exact same size and shape (congruent). transformation: The mapping, or movement, of all the points of a figure in a plane according to a common operation. reflection: A transformation that "flips" a figure over a line of reflection. -
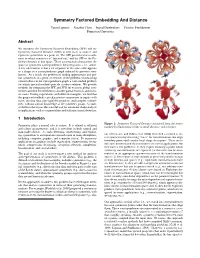
Symmetry Factored Embedding and Distance
Symmetry Factored Embedding And Distance Yaron Lipman Xiaobai Chen Ingrid Daubechies Thomas Funkhouser Princeton University Abstract We introduce the Symmetry Factored Embedding (SFE) and the Symmetry Factored Distance (SFD) as new tools to analyze and represent symmetries in a point set. The SFE provides new coordi- nates in which symmetry is “factored out,” and the SFD is the Eu- clidean distance in that space. These constructions characterize the space of symmetric correspondences between points – i.e., orbits. A key observation is that a set of points in the same orbit appears as a clique in a correspondence graph induced by pairwise simi- larities. As a result, the problem of finding approximate and par- tial symmetries in a point set reduces to the problem of measuring connectedness in the correspondence graph, a well-studied problem for which spectral methods provide a robust solution. We provide methods for computing the SFE and SFD for extrinsic global sym- metries and then extend them to consider partial extrinsic and intrin- sic cases. During experiments with difficult examples, we find that the proposed methods can characterize symmetries in inputs with noise, missing data, non-rigid deformations, and complex symme- tries, without a priori knowledge of the symmetry group. As such, we believe that it provides a useful tool for automatic shape analysis in applications such as segmentation and stationary point detection. 1 Introduction Figure 1: Symmetry Factored Distance measured from the points Symmetry plays a central role in nature. It is related to efficient marked by black arrows (blue is small distance, red is large). -

Transformations to Show Congruence and Similarity
California State University, San Bernardino CSUSB ScholarWorks Electronic Theses, Projects, and Dissertations Office of aduateGr Studies 6-2015 Discovering and Applying Geometric Transformations: Transformations to Show Congruence and Similarity Tamara V. Bonn California State University - San Bernardino Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd Part of the Science and Mathematics Education Commons Recommended Citation Bonn, Tamara V., "Discovering and Applying Geometric Transformations: Transformations to Show Congruence and Similarity" (2015). Electronic Theses, Projects, and Dissertations. 150. https://scholarworks.lib.csusb.edu/etd/150 This Thesis is brought to you for free and open access by the Office of aduateGr Studies at CSUSB ScholarWorks. It has been accepted for inclusion in Electronic Theses, Projects, and Dissertations by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. DISCOVERING AND APPLYING GEOMETRIC TRANSFORMATIONS: TRANSFORMATIONS TO SHOW CONGRUENCE AND SIMILARITY A Thesis Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degree Master of Arts in Teaching: Mathematics by Tamara Lee Voorhies Bonn June 2015 DISCOVERING AND APPLYING GEOMETRIC TRANSFORMATIONS: TRANSFORMATIONS TO SHOW CONGRUENCE AND SIMILARITY A Thesis Presented to the Faculty of California State University, San Bernardino by Tamara Lee Voorhies Bonn June 2015 Approved by: Dr. John Sarli, Committee Chair, Mathematics Dr. Davida Fischman, Committee Member Dr. Catherine Spencer, Committee Member Copyright 2015 Tamara Lee Voorhies Bonn ABSTRACT The use and application of geometric transformations is a fundamental standard for the Common Core State Standards. This study was developed to determine current high school teachers’ prior mathematical content knowledge and develop their content knowledge of transformations and their applications. -

Basic Transformation Geometry
Basic Transformation Geometry For transformation geometry there are two basic types: rigid transformations and non-rigid transformations. This page will deal with three rigid transformations known as translations, reflections and rotations. The Vocabulary of Transformation Geometry In short, a transformation is a copy of a geometric figure, where the copy holds certain properties. Think of when you copy/paste a picture on your computer. The original figure is called the pre-image; the new (copied) picture is called theimage of the transformation. A rigid transformation is one in which the pre-image and the image both have the exact same size and shape. Translations - Each Point is Moved the Same Way The most basic transformation is the translation. The formal definition of a translation is "every point of the pre-image is moved the same distance in the same direction to form the image." Take a look at the picture below for some clarification. Each translation follows a rule. In this case, the rule is "5 to the right and 3 up." You can also translate a pre-image to the left, down, or any combination of two of the four directions. More advanced transformation geometry is done on the coordinate plane. The transformation for this example would be T(x, y) = (x+5, y+3). Reflections - Like Looking in a Mirror A reflection is a "flip" of an object over a line. Let's look at two very common reflections: a horizontal reflection and a vertical reflection. Notice the colored vertices for each of the triangles. The line of reflection is equidistant from both red points, blue points, and green points. -

Review Rigid Transformations, Kinematics, and Dynamics Due: Thursday Feb
EE106b - Spring 2017 Assignment 1 Assignment 1: Review Rigid Transformations, Kinematics, and Dynamics Due: Thursday Feb. 2, 2017 at 9:30am This assignment covers material from MLS Chapters 2-4. Your homework will be submitted electronically through GradeScope. No hardcopies will be accepted. We don't mind if you work with other students on your homework. However, each student must write up and turn in their own assignment (i.e. no copy & paste). If you worked with other students, please acknowledge who you worked with at the top of your homework. Question 1. (10 points) Properties of rotation matrices. MLS Problem 2.3 Answer: 3 Part a. Let ! 2 R such that k!k2 = 1. Then 2 3 s !3 −!2 2 det(sI − !^) = det 4 −!3 s !1 5 = s(s − 1) !2 −!1 s 2 Solving s(s − 1) = 0 yields the eigenvalues s1 = 0; s2 = +i; s3 = −i. 3 Let (x1; x2;!) be a right-handed orthonormal basis for R . Then the eigenvectors are v1 = !, v2 = x1 + ix2 and v3 = x1 − ix2. Part b. Let vi be an eigenvector of! ^. The key idea is to expand out the exponential: 1 e!θ^ v = (I +!θ ^ + (^!θ)2 + :::)v i 2! i 1 = v + s θv + (s θ)2v + ::: i i i 2! i i siθ = e vi Thus the eigenvalues of e!θ^ are 1; eiθ, and e−iθ, and the eigenvector whose eigenvalues are 1 is !. Part c. Let 2 3 r11 r12 r13 R = 4 r21 r22 r23 5 r31 r32 r33 Using cofactors we get det(R) = r11(r22r33 − r23r32) + r21(r32r13 − r12r33) + r31(r12r23 − r22r13) = r1 · (r2 × r3) Question 2. -

3D Photography: Point Based Rigid Registration Homework Due: Wed., Oct
3D Photography: Point Based Rigid Registration Homework due: Wed., Oct. 9, in class. The subject of this homework is point based rigid registration. Registration is the task of finding a transformation from one coordinate system to another so that all features that appear in both data sets are aligned with each other. In this homework, we limit ourselves to rigid transformations with input given as points. THis means we need to find 3 translational parameters and 3 rotational parameters. Problem Definition Given the coordinates of points measured in two cartesian coordinate systems, find the rigid transformation between the two systems. Once we have this transformation, we can transform points in on coordinate system to the other. 1 Three Point Registration Given the coordinates of three points in two coordinate systems, let us call them \left" and \right". The points are pr1; pr2; pr3. We find the transformation between coordinate systems with the following construction: 1. Choose one of the points to be the origin, let us say p1. 2. Construct the x axis: p2 − p1 x = jp2 − p1j 3. Construct the y axis: y = (p3 − p1) − [(p3 − p1) · x]x y y = jyj 4. Construct the z axis: z = x × y 5. Build the rotation matrices for both point sets: Rl = [xl; yl; zl] Rr = [xr; yr; zr] 6. The rotation between the \right" coordinate system to the \left" is given by: t R = RlRr 7. The translation between the \right" coordinate system to the \left" is given by: t = pl1 − Rpr1 This assumes we have a \match" of the 3 points in each data set with the other.