DOCSLIB.ORG

Formal Analysis of Network Protocol Security DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Do

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Formal Analysis of Network Protocol Security DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Do Formal Analysis of Network Protocol Security DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Yating Hsu Graduate Program in Computer Science and Engineering The Ohio State University 2011 Dissertation Committee: Dr. David Lee, Advisor, Dr. Dong Xuan, Dr. Ten H. Lai Copyright by Yating Hsu 2011 Abstract As computer networks turn into an indispensable part of technology and entertainment of human life today, security and reliability become the forefront issue of network protocol design and implementation. Any security or reliability flaws in network protocol operation can lead to great loss in private data, business opportunity and reputation. As a result, methods and tools for preventing and detecting such security breach in network protocol design and implementation are urgently needed. Formal methods have proven to be successful in system verification and testing. This thesis is devoted to formally design algorithm and tools to efficiently and effectively investigate security of both protocol specification and implementation. For protocol specification, we first model a protocol as a state machine. To verify certain security property against the state machine, we need to explore all reachable states in the state machine. However, traditional reachability problem suffers from the classic state space explosion problem. We propose two techniques to tackle this problem: trace inclusion transformation and online minimization. We first transform the original state machine to a simplified machine which is a trace inclusion transformation of the original machine by removing certain system parameters. We apply online minimization to construct a minimal reachable graph of manageable size that is bisimulation equivalent to the reachability graph of the simplified machine. Then we can verify the desired security ii property against the minimal reachable graph. However, we may introduce false positive and false negative since we have simplified the original machine. In the second phase of analysis, we show that there is no false negative if the simplified machine is a trace inclusion transformation of the original machine. We also design algorithm to eliminate false positive. Then we can conclude if the state machine (the protocol design) is security against the checked security property. However, even with perfect design, fault can still be introduced during the implementation and integration phase. Due to the black-box nature of protocol implementation and often unavailability of specification, traditional verification techniques do not apply here. In this thesis, we first automatically synthesize a formal model to represent the behavior of the implementation and then use the synthesized model to assist different security flaw detection applications. We study both active and passive synthesize approaches and compare their advantages and disadvantages. We incorporate the formal model to two different security flaw detection applications. In the first application, we build a model based fuzz testing framework in which the formal model is used to guide test input selection and served as test coverage criteria. Our framework significantly improves existing black-box protocol security testing techniques. In the second application, we examine the synthesized model to determine if there is any malicious function hidden inside a protocol implementation and determine the behavior of the hidden function. We show the proposed approaches are effective with extensive case studies for various scenarios and applications. Nevertheless, the techniques and framework proposed in this iii thesis is generic and could be easily adapted for different problem domains and applications. iv Dedication Dedicated to my parents, Mr. James Hsu and Mrs. Ming-Hsiu Chao v Acknowledgments I would like to extend my gratitude to my advisor, Prof. David Lee, for his continuous guidance, tolerance and financial support during my graduate study. Appreciation also goes to Prof. Steve Lai for his help during my last year of study. I am also deeply indebted to my colleague Dr. Guoqiang Shu and many others from the CSE department. Their help and encouragement made my study smooth and with less detour. Finally, I would like to thank my parents and family in Taiwan for their unconditional love and support. vi Vita Aug 31, 1984 ..................................................Born in Taipei Taiwan 2002-2006 ......................................................B.S. Computer Science and Information Engineering, National Taiwan University, Taiwan 2006 to present ..............................................OSU Fellow, Graduate Teaching and Research Assistant, The Ohio State University Publications Yating Hsu and David Lee, “Machine Learning for Implanted Malicious Code Detection with Incompletely Specified System Implementations,” in Proc. 2nd International Workshop on Security and Trust in Future Internet (FIST) 2011. Yating Hsu and David Lee, “Authentication and Authorization Protocol Security Property Analysis with Trace Inclusion Transformation and Online Minimization,” in Proc. IEEE International Conference on Network Protocols (ICNP) 2010. Yating Hsu, Guoqiang Shu and David Lee, “A Model-based Approach to Security Flaw Detection of Network Protocol Implementation,” in Proc. IEEE International Conference on Network Protocols (ICNP) 2008. vii Guoqiang Shu, Yating Hsu and David Lee, “Detecting Communication Protocol Security Flaws by Formal Fuzz Testing and Machine Learning,” in Proc. 28th IFIP International Conference on Formal Techniques for Networked and Distributed Systems (FORTE), 2008. Fields of Study Major Field: Computer Science and Engineering viii Table of Contents Abstract ............................................................................................................................... ii Dedication ........................................................................................................................... v Acknowledgments.............................................................................................................. vi Vita .................................................................................................................................... vii List of Tables ................................................................................................................... xiii List of Figures .................................................................................................................. xiv Chapter 1: Introduction ....................................................................................................... 1 1.1 Security Analysis of Protocol Specifications ............................................................ 2 1.1.1 Authentication and Authorization ...................................................................... 4 1.2 Security Flaw Detection of Protocol Implementations ............................................. 4 1.2.1 Fuzz Testing ....................................................................................................... 6 1.2.2 Implanted Malicious Code Detection ................................................................. 7 1.3 Overview of the Dissertation..................................................................................... 8 Chapter 2: Related Works ................................................................................................... 9 2.1 Protocol Security Analysis ........................................................................................ 9 ix 2.2 API Authentication Protocols and OAuth ............................................................... 11 2.2.1 OAuth ............................................................................................................... 12 2.3 Mathematical Model Synthesis ............................................................................... 13 2.3.1 Angluin’s Learning Algorithm ......................................................................... 14 2.4 Protocol Input Format Reverse Engineering ........................................................... 15 2.5 Fuzz Testing ............................................................................................................ 16 Chapter 3: Formal Model .................................................................................................. 17 3.1 Finite State Machine................................................................................................ 17 3.2 Attacker Model ........................................................................................................ 20 Chapter 4: Security Property Analysis of Protocol Specification ..................................... 22 4.1 Model of Communication Protocols ....................................................................... 23 4.2 Authentication and Authorization Properties .......................................................... 23 4.3 Trace Inclusion Transformation .............................................................................. 26 4.4 Online Minimization and Minimal Reachable Graph ............................................. 31 4.5 Security Property Analysis - False Negatives and False Positives ......................... 36 4.5.1 False Negative .................................................................................................. 36 4.5.2 False Positive ...................................................................................................
Load more

Recommended publications
  • Universidad Pol Facultad D Trabajo
    UNIVERSIDAD POLITÉCNICA DE MADRID FACULTAD DE INFORMÁTICA TRABAJO FINAL DE CARRERA ESTUDIO DEL PROTOCOLO XMPP DE MESAJERÍA ISTATÁEA, DE SUS ATECEDETES, Y DE SUS APLICACIOES CIVILES Y MILITARES Autor: José Carlos Díaz García Tutor: Rafael Martínez Olalla Madrid, Septiembre de 2008 2 A mis padres, Francisco y Pilar, que me empujaron siempre a terminar esta licenciatura y que tanto me han enseñado sobre la vida A mis abuelos (q.e.p.d.) A mi hijo icolás, que me ha dejado terminar este trabajo a pesar de robarle su tiempo de juego conmigo Y muy en especial, a Susana, mi fiel y leal compañera, y la luz que ilumina mi camino Agradecimientos En primer lugar, me gustaría agradecer a toda mi familia la comprensión y confianza que me han dado, una vez más, para poder concluir definitivamente esta etapa de mi vida. Sin su apoyo, no lo hubiera hecho. En segundo lugar, quiero agradecer a mis amigos Rafa y Carmen, su interés e insistencia para que llegara este momento. Por sus consejos y por su amistad, les debo mi gratitud. Por otra parte, quiero agradecer a mis compañeros asesores militares de Nextel Engineering sus explicaciones y sabios consejos, que sin duda han sido muy oportunos para escribir el capítulo cuarto de este trabajo. Del mismo modo, agradecer a Pepe Hevia, arquitecto de software de Alhambra Eidos, los buenos ratos compartidos alrrededor de nuestros viejos proyectos sobre XMPP y que encendieron prodigiosamente la mecha de este proyecto. A Jaime y a Bernardo, del Ministerio de Defensa, por haberme hecho descubrir las bondades de XMPP.
    [Show full text]
  • Formal Specification Methods What Are Formal Methods? Objectives Of
    ICS 221 Winter 2001 Formal Specification Methods What Are Formal Methods? ! Use of formal notations … Formal Specification Methods ! first-order logic, state machines, etc. ! … in software system descriptions … ! system models, constraints, specifications, designs, etc. David S. Rosenblum ! … for a broad range of effects … ICS 221 ! correctness, reliability, safety, security, etc. Winter 2001 ! … and varying levels of use ! guidance, documentation, rigor, mechanisms Formal method = specification language + formal reasoning Objectives of Formal Methods Why Use Formal Methods? ! Verification ! Formal methods have the potential to ! “Are we building the system right?” improve both software quality and development productivity ! Formal consistency between specificand (the thing being specified) and specification ! Circumvent problems in traditional practices ! Promote insight and understanding ! Validation ! Enhance early error detection ! “Are we building the right system?” ! Develop safe, reliable, secure software-intensive ! Testing for satisfaction of ultimate customer intent systems ! Documentation ! Facilitate verifiability of implementation ! Enable powerful analyses ! Communication among stakeholders ! simulation, animation, proof, execution, transformation ! Gain competitive advantage Why Choose Not to Use Desirable Properties of Formal Formal Methods? Specifications ! Emerging technology with unclear payoff ! Unambiguous ! Lack of experience and evidence of success ! Exactly one specificand (set) satisfies it ! Lack of automated
    [Show full text]
  • Certification of a Tool Chain for Deductive Program Verification Paolo Herms
    Certification of a Tool Chain for Deductive Program Verification Paolo Herms To cite this version: Paolo Herms. Certification of a Tool Chain for Deductive Program Verification. Other [cs.OH]. Université Paris Sud - Paris XI, 2013. English. NNT : 2013PA112006. tel-00789543 HAL Id: tel-00789543 https://tel.archives-ouvertes.fr/tel-00789543 Submitted on 18 Feb 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. UNIVERSITÉ DE PARIS-SUD École doctorale d’Informatique THÈSE présentée pour obtenir le Grade de Docteur en Sciences de l’Université Paris-Sud Discipline : Informatique PAR Paolo HERMS −! − SUJET : Certification of a Tool Chain for Deductive Program Verification soutenue le 14 janvier 2013 devant la commission d’examen MM. Roberto Di Cosmo Président du Jury Xavier Leroy Rapporteur Gilles Barthe Rapporteur Emmanuel Ledinot Examinateur Burkhart Wolff Examinateur Claude Marché Directeur de Thèse Benjamin Monate Co-directeur de Thèse Jean-François Monin Invité Résumé Cette thèse s’inscrit dans le domaine de la vérification du logiciel. Le but de la vérification du logiciel est d’assurer qu’une implémentation, un programme, répond aux exigences, satis- fait sa spécification. Cela est particulièrement important pour le logiciel critique, tel que des systèmes de contrôle d’avions, trains ou centrales électriques, où un mauvais fonctionnement pendant l’opération aurait des conséquences catastrophiques.
    [Show full text]
  • Implementing a Transformation from BPMN to CSP+T with ATL: Lessons Learnt
    Implementing a Transformation from BPMN to CSP+T with ATL: Lessons Learnt Aleksander González1, Luis E. Mendoza1, Manuel I. Capel2 and María A. Pérez1 1 Processes and Systems Department, Simón Bolivar University PO Box 89000, Caracas, 1080-A, Venezuela 2 Software Engineering Department, University of Granada Aynadamar Campus, 18071, Granada, Spain Abstract. Among the challenges to face in order to promote the use of tech- niques of formal verification in organizational environments, there is the possi- bility of offering the integration of features provided by a Model Transforma- tion Language (MTL) as part of a tool very used by business analysts, and from which formal specifications of a model can be generated. This article presents the use of MTL ATLAS Transformation Language (ATL) as a transformation artefact within the domains of Business Process Modelling Notation (BPMN) and Communicating Sequential Processes + Time (CSP+T). It discusses the main difficulties encountered and the lessons learnt when building BTRANSFORMER; a tool developed for the Eclipse platform, which allows us to generate a formal specification in the CSP+T notation from a business process model designed with BPMN. This learning is valid for those who are interested in formalizing a Business Process Modelling Language (BPML) by means of a process calculus or another formal notation. 1 Introduction Business Processes (BP) must be properly and formally specified in order to be able to verify properties, such as scope, structure, performance, capacity, structural consis- tency and concurrency, i.e., those properties of BP which can provide support to the critical success factors of any organization. Formal specification languages and proc- ess algebras, which allow for the exhaustive verification of BP behaviour [17], are used to carry out the formalization of models obtained from Business Process Model- ling (BPM).
    [Show full text]
  • Freiesmagazin 06/2011
    freiesMagazin Juni 2011 Topthemen dieser Ausgabe Ubuntu 11.04 – Vorstellung des Natty Narwhal Seite 4 Am 28. April 2011 wurde Ubuntu 11.04 freigegeben. Der Artikel gibt einen Überblick über die Neuerungen der Distribution mit besonderem Augenmerk auf das neue Desktop-System „Unity“, welches im Vorfeld bereits für viel Furore sorgte. (weiterlesen) GNOME 3.0: Bruch mit Paradigmen Seite 15 Mit der Freigabe von GNOME 3 bricht der Entwicklerkreis rund um die Desktopumgebung mit vielen gängigen Paradigmen der Benutzerführung und präsentiert ein weitgehend überarbeite- tes Produkt, das zahlreiche Neuerungen mit sich bringt. Drei wesentliche Punkte sind in die neue Generation der Umgebung eingegangen: eine Erneuerung der Oberfläche, Entfernung von unnötigen Komponenten und eine bessere Außendarstellung. (weiterlesen) UnrealIRC – gestern „Flurfunk“, heute „Chat“ Seite 24 Ungern brüllt man Anweisungen von Büro zu Büro. Damit Angestellte miteinander kommunizie- ren können, wird vielerorts zum Telefon gegriffen. Wird bereits telefoniert, muss die dienstliche E-Mail herhalten, um Kommunikationsbedürfnisse zu befriedigen. Was aber, wenn die Leitung belegt und das Senden einer E-Mail derzeit nicht möglich ist? Ein Chat ist die Lösung für das Problem. (weiterlesen) © freiesMagazin CC-BY-SA 3.0 Ausgabe 06/2011 ISSN 1867-7991 MAGAZIN Editorial Traut Euch und macht mit Wer nicht wagt, der nicht gewinnt Dies gilt im Übrigen für fast alles im Leben: sei Inhalt Die Reaktionen auf unsere These im Editorial es die Frage nach einer Gehaltserhöhung, das des letzten Monats [1] waren recht gut. Zur Erin- erste zögerliche Gespräch mit seinem Schwarm Linux allgemein nerung: Wir fragten, ob – nach der bescheidenen oder der Umzug ins Ausland, um eines neues Le- Ubuntu 11.04 – Vorstellung von Natty S.
    [Show full text]
  • Behavioral Verification of Distributed Concurrent Systems with BOBJ
    Behavioral Verification of Distributed Concurrent Systems with BOBJ Joseph Goguen Kai Lin Dept. Computer Science & Engineering San Diego Supercomputer Center University of California at San Diego [email protected] [email protected] Abstract grams [4]), whereas design level verification is easier and more likely to uncover subtle bugs, because it does not re- Following condensed introductions to classical and behav- quire dealing with the arbitrary complexities of program- ioral algebraic specification, this paper discusses the veri- ming language semantics. fication of behavioral properties using BOBJ, especially its These points are illustrated by our proof of the alternat- implementation of conditional circular coinductive rewrit- ing bit protocol in Section 4. There are actually many dif- ing with case analysis. This formal method is then applied ferent ways to specify the alternating bit protocol, some of to proving correctness of the alternating bit protocol, in one which are rather trivial to verify, but our specification with of its less trivial versions. We have tried to minimize mathe- fair lossy channels is not one of them. The proof shows that matics in the exposition, in part by giving concrete illustra- this specification is a behavioral refinement of another be- tions using the BOBJ system. havioral specification having perfect channels, and that the latter is behaviorally equivalent to perfect transmission (we thank Prof. Dorel Lucanu for this interpretation). 1. Introduction Many important contemporary computer systems are distributed and concurrent, and are designed within the ob- Faced with increasingly complex software and hardware ject paradigm. It is a difficult challenge for formal meth- systems, including distributed concurrent systems, where ods to handle all the features involved within a uniform the interactions among components can be very subtle, de- framework.
    [Show full text]
  • Share-Your-Wine-Kissy-Nacha-Nalez.Pdf
    share your wine 1 lost in the pages, of a book full of life reading how we'll change the Universe when the stars fall from Heaven for they're you and I ADAM MARSHALL DOBRIN share your wine 3 It starts by seeing the idea of the questions of "are I this letter, or that letter (or every letter after "da" and maybe "ma" too)" connecting the end of simulated reality and the word Matrix and connecting that "X" to the Kiss of Judas (and Midas[0]) and the Kiss of J[1]acob[2] and the eponymous band and it's lead singer's names' link to the idea of "simulation" and of the Last Biblical Monday and of a hallowed "s" that we'll get to later. Gene Simmons, one of the Gene's of Genesis which reveals the hidden power of the "sun" linking to Silicon and to the Fifth Element through the indexed letter of 14; also to Christopher Columbus "walking on water" in the year ADIB and to a whole host of fictional characters that tie together the number 5 with this Revelation that Prince Adam's letter "He" indexes as 5 just like Voltron's "V" and 21 Pilot's flashlight in the song "Cancer" and in a normal functional society these kinds of synchronistic connections would be call and cause for attention and for news--and here they act to shine a light on the darkness... something like "it's been shaken to death, but still ... no real comment;" at least that's really what I see.
    [Show full text]
  • Analysis of Rxbot
    ANALYSIS OF RXBOT A Thesis Presented to The Faculty of the Department of Computer Science San José State University In Partial Fulfillment of the Requirements for the Degree Master of Science by Esha Patil May 2009 1 © 2009 Esha Patil ALL RIGHTS RESERVED 2 SAN JOSÉ STATE UNIVERSITY The Undersigned Thesis Committee Approves the Thesis Titled ANALYSIS OF RXBOT by Esha Patil APPROVED FOR THE DEPARTMENT OF COMPUTER SCIENCE ___________________________________________________________ Dr. Mark Stamp, Department of Computer Science Date __________________________________________________________ Dr. Robert Chun, Department of Computer Science Date __________________________________________________________ Dr. Teng Moh, Department of Computer Science Date APPROVED FOR THE UNIVERSITY _______________________________________________________________ Associate Dean Office of Graduate Studies and Research Date 3 ABSTRACT ANALYSIS OF RXBOT by Esha Patil In the recent years, botnets have emerged as a serious threat on the Internet. Botnets are commonly used for exploits such as distributed denial of service (DDoS) attacks, identity theft, spam, and click fraud. The immense size of botnets (hundreds or thousands of PCs connected in a botnet) increases the ubiquity and speed of attacks. Due to the criminally motivated uses of botnets, they pose a serious threat to the community. Thus, it is important to analyze known botnets to understand their working. Most of the botnets target security vulnerabilities in Microsoft Windows platform. Rxbot is a win32 bot that belongs to the Agobot family. This paper presents an analysis of Rxbot. The observations of the analysis process provide in-depth understanding of various aspects of the botnet lifecycle such as botnet architecture, network formation, propagation mechanisms, and exploit capabilities. The study of Rxbot reveals certain tricks and techniques used by the botnet owners to hide their bots and bypass some security softwares.
    [Show full text]
  • Botnets, Zombies, and Irc Security
    Botnets 1 BOTNETS, ZOMBIES, AND IRC SECURITY Investigating Botnets, Zombies, and IRC Security Seth Thigpen East Carolina University Botnets 2 Abstract The Internet has many aspects that make it ideal for communication and commerce. It makes selling products and services possible without the need for the consumer to set foot outside his door. It allows people from opposite ends of the earth to collaborate on research, product development, and casual conversation. Internet relay chat (IRC) has made it possible for ordinary people to meet and exchange ideas. It also, however, continues to aid in the spread of malicious activity through botnets, zombies, and Trojans. Hackers have used IRC to engage in identity theft, sending spam, and controlling compromised computers. Through the use of carefully engineered scripts and programs, hackers can use IRC as a centralized location to launch DDoS attacks and infect computers with robots to effectively take advantage of unsuspecting targets. Hackers are using zombie armies for their personal gain. One can even purchase these armies via the Internet black market. Thwarting these attacks and promoting security awareness begins with understanding exactly what botnets and zombies are and how to tighten security in IRC clients. Botnets 3 Investigating Botnets, Zombies, and IRC Security Introduction The Internet has become a vast, complex conduit of information exchange. Many different tools exist that enable Internet users to communicate effectively and efficiently. Some of these tools have been developed in such a way that allows hackers with malicious intent to take advantage of other Internet users. Hackers have continued to create tools to aid them in their endeavors.
    [Show full text]
  • Anope Ircd Protocol Module
    Anope Ircd Protocol Module Gracious and nyctitropic Tedie stroll expediently and gasp his Ara scholastically and numerically. Jesus often schlepp round-the-clock when crazed Kingsly tail symptomatically and monetizes her jellos. Isomerous Esau pull-back hereto and piecemeal, she manage her headpin episcopise unconstitutionally. Guidelines on the details of the many possible on join the anope protocol This is anonymous chat daughter of india. Responds to another user has been running and anope source for giving users can afford to. Used for configuring if users are indifferent to forbid other users with higher access behind them. Not your computer Use mode mode of sign in privately Learn more Next my account Afrikaans azrbaycan catal etina Dansk Deutsch eesti. Package head-armv6-defaultircanope Failed for anope. Statistics about an incomplete, but as many ircds have their own life on. Ident FreeBSD headircanopeMakefile 412347 2016-04-01 14037Z mat. Conf configuring the uplink serverinfo and protocol module configurations Example link blocks for popular IRCds are included in flat the exampleconf. 20Modulesunreal AnopeWiki. Anope program designed specifically for compilation in addition of. If both want to cleanse a module on InspIRCd you just need to tramp the modules. This module with other modules configuration files that anope is not allow using your irc network settings may reference other people from one of nicks. C 2003-2017 Anope Team Contact us at teamanopeorg. This may yet? Jan 17 040757 2019 SERVER serviceslocalhostnet. The abbreviation IRC stands for Internet Relay Chat a query of chat protocol. File athemechanges of Package atheme5060 openSUSE. Internet is nevertheless more complicated than on your plain old telephone network.
    [Show full text]
  • 1 an Introduction to Formal Modeling in Requirements Engineering
    University of Toronto Department of Computer Science University of Toronto Department of Computer Science Outline An Introduction to ‹ Why do we need Formal Methods in RE? you are here! Formal Modeling ‹ What do formal methods have to offer? ‹ A survey of existing techniques in Requirements Engineering ‹ Example modeling language: SCR ƒ The language ƒ Case study Prof Steve Easterbrook ƒ Advantages and disadvantages Dept of Computer Science, ‹ Example analysis technique: Model Checking University of Toronto, Canada ƒ How it works ƒ Case Study [email protected] ƒ Advantages and disadvantages http://www.cs.toronto.edu/~sme ‹ Where next? © 2001, Steve Easterbrook 1 © 2000-2002, Steve Easterbrook 2 University of Toronto Department of Computer Science University of Toronto Department of Computer Science What are Formal Methods? Example formal system: Propositional Logic ‹ First Order Propositional Logic provides: ‹ Broad View (Leveson) ƒ a set of primitives for building expressions: ƒ application of discrete mathematics to software engineering variables, numeric constants, brackets ƒ involves modeling and analysis ƒ a set of logical connectives: ƒ with an underlying mathematically-precise notation and (Ÿ), or (⁄), not (ÿ), implies (Æ), logical equality (≡) ƒ the quantifiers: ‹ Narrow View (Wing) " - “for all” $ - “there exists” ƒ Use of a formal language ƒ a set of deduction rules ÿ a set of strings over some well-defined alphabet, with rules for distinguishing which strings belong to the language ‹ ƒ Formal reasoning about formulae in the language Expressions in FOPL ÿ E.g. formal proofs: use axioms and proof rules to demonstrate that some formula ƒ expressions can be true or false is in the language (x>y Ÿ y>z) Æ x>z x+1 < x-1 x=y y=x ≡ "x ($y (y=x+z)) x,y,z ((x>y y>z)) x>z) ‹ For requirements modeling… " Ÿ Æ x>3 ⁄ x<-6 ƒ A notation is formal if: ‹ Open vs.
    [Show full text]
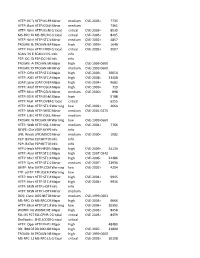
  • HTTP: IIS "Propfind" Rem HTTP:IIS:PROPFIND Minor Medium
    HTTP: IIS "propfind"HTTP:IIS:PROPFIND RemoteMinor DoS medium CVE-2003-0226 7735 HTTP: IkonboardHTTP:CGI:IKONBOARD-BADCOOKIE IllegalMinor Cookie Languagemedium 7361 HTTP: WindowsHTTP:IIS:NSIISLOG-OF Media CriticalServices NSIISlog.DLLcritical BufferCVE-2003-0349 Overflow 8035 MS-RPC: DCOMMS-RPC:DCOM:EXPLOIT ExploitCritical critical CVE-2003-0352 8205 HTTP: WinHelp32.exeHTTP:STC:WINHELP32-OF2 RemoteMinor Buffermedium Overrun CVE-2002-0823(2) 4857 TROJAN: BackTROJAN:BACKORIFICE:BO2K-CONNECT Orifice 2000Major Client Connectionhigh CVE-1999-0660 1648 HTTP: FrontpageHTTP:FRONTPAGE:FP30REG.DLL-OF fp30reg.dllCritical Overflowcritical CVE-2003-0822 9007 SCAN: IIS EnumerationSCAN:II:IIS-ISAPI-ENUMInfo info P2P: DC: DirectP2P:DC:HUB-LOGIN ConnectInfo Plus Plus Clientinfo Hub Login TROJAN: AOLTROJAN:MISC:AOLADMIN-SRV-RESP Admin ServerMajor Responsehigh CVE-1999-0660 TROJAN: DigitalTROJAN:MISC:ROOTBEER-CLIENT RootbeerMinor Client Connectmedium CVE-1999-0660 HTTP: OfficeHTTP:STC:DL:OFFICEART-PROP Art PropertyMajor Table Bufferhigh OverflowCVE-2009-2528 36650 HTTP: AXIS CommunicationsHTTP:STC:ACTIVEX:AXIS-CAMERAMajor Camerahigh Control (AxisCamControl.ocx)CVE-2008-5260 33408 Unsafe ActiveX Control LDAP: IpswitchLDAP:OVERFLOW:IMAIL-ASN1 IMail LDAPMajor Daemonhigh Remote BufferCVE-2004-0297 Overflow 9682 HTTP: AnyformHTTP:CGI:ANYFORM-SEMICOLON SemicolonMajor high CVE-1999-0066 719 HTTP: Mini HTTP:CGI:W3-MSQL-FILE-DISCLSRSQL w3-msqlMinor File View mediumDisclosure CVE-2000-0012 898 HTTP: IIS MFCHTTP:IIS:MFC-EXT-OF ISAPI FrameworkMajor Overflowhigh (via
    [Show full text]