Industrial Location, Spatial Discrete Choice Models and the Need to Account for Neighbourhood Effects
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Destination Region of Murcia
PRESS Destination Region of Murcia Region of Murcia The Region of Murcia is located in south-east Spain on what is known as the Mediterranean Arc. Set between two seas –the Mediterranean and the Mar Menor– as a region, it has succeeded in combining its extensive cultural heritage with innovation and avant-garde artistic tendencies. Its most important cities are Murcia, the capital, with more than 440,000 inhabitants, Cartagena with more than 214,000 and Lorca with more than 90,000. The Region of Murcia has a population of around one and a half million and covers an area of 11,300km2. Although it is not a very large region, it offers 252km of coast and an astonishing variety of different landscapes considering its size. Diverse and accessible, it only takes a few hours to travel the length and breadth of the region. Mountains, beaches and cities dot the landscape and visitors will find history at every turn. Another of the Region of Murcia’s main attractions is its particularly good weather, with average temperatures in excess of 19ºC and 315 days of sun a year. All these factors offer visitors the opportunity to choose between a wide range of alternatives when organising their stay in the Region of Murcia. It is a destination full of contrasts, where everything is close at hand and easily accessible. Although the driving force behind the Region of Murcia’s economy has traditionally been agriculture, the Regional Government has made a firm commitment to converting the tourist sector into one of the pillars of the region’s economy. -

PLAN DE VIGILANCIA ENTOMOLÓGICA Índice
PLAN DE VIGILANCIA ENTOMOLÓGICA 2019 Índice Muestreo 1.Semanas 16-18. 16-30 abril...................................................................................1 Muestreo 2.Semanas 18-20. 30 abril-14 mayo........................................................................3 Muestreo 3.Semanas 20-22. 14-28 mayo.................................................................................5 Muestreo 4.Semanas 22-24. 28 mayo-11 junio........................................................................7 Muestreo 5.Semanas 24-26. 11-25 junio..................................................................................9 Muestreo 6.Semanas 26-28. 25 junio-9 julio.........................................................................11 Muestreo 7.Semanas 28-30. 9-23 julio...................................................................................13 Muestreo 8.Semanas 30-32. 23 julio-6 agosto.......................................................................15 Muestreo 9.Semanas 32-34. 6-20 agosto................................................................................17 Muestreo 10.Semanas 34-36. 20 agosto-3 septiembre..........................................................19 Muestreo 11.Semanas 36-38. 3-17 septiembre......................................................................21 Muestreo 12.Semanas 38-40. 17 septiembre-1 octubre........................................................23 Muestreo 13.Semanas 40-42. 1-15 octubre............................................................................25 -
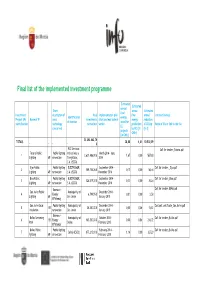
Final List of the Implemented Investment Programme
Final list of the implemented investment programme Estimated Estimated annual Short annual Estimated final Investment description of Real Implementation plan final annual contract Invoice Identification energy Project (IP) Name of IP area/ investments (start and end date of energy reduction of investor saved for identification technology carried out works) production of CO2eq Name of file or link to the file EE concerned by RES [in [in t] projects GWh] [in GWh] 33. 243 .682 ,74 TOTALS 28,88 4,01 10.502,39 € FCC Servicios Call for tenders_Totana.pdf Totana Public Public lighting Industriales y March 2014 – June 1 2.621.486,90 € 1,67 0,00 567,80 Lighting AP renovation Energéticos, 2014 S.A. (ESCO) Ojos Public Public lighting ELECTROMUR, September 2014 - Call for tenders _Oj¢s.pdf 2 109.156,26 € 0,17 0,00 56,44 Lighting AP renovation S.A. (ESCO) November 2014 Ulea Public Public lighting ELECTROMUR, September 2014 - Call for tenders_Ulea.pdf 3 124.519,30 € 0,33 0,00 38,24 Lighting AP renovation S.A. (ESCO) November 2014 Biomass + Call for tenders BORM.pdf San Javier Public Municipality of December 2014 - 4 Energy 6.799,95 € 0,01 0,00 2,50 Lighting AP San Javier January 2015 Efficiency San Javier Solar Public lighting Municipality of December 2014 - Contract certificate_San Javier.pdf 5 ER 30.250,00 € 0,00 0,06 15,12 instalation renovation San Javier January 2015 Biomass + Bullas Swimming Municipality of October 2014 - Call for tenders_Bullas.pdf 6 ER Energy 163.350,00 € 0,00 0,86 216,72 Pool Bullas February 2015 Efficiency Bullas Public Public lighting February 2014 - Call for tenders_Bullas.pdf 7 Cofely (ESCO) 877.215,10 € 1,14 0,00 327,20 lighting AP renovation February 2015 Las Torres de Public lighting FERROVIAL February 2015 - June Call for tenders_Las Torres de 8 Cotillas Public 2.351.597,54 € 1,59 0,00 540,45 AP renovation Servicios (ESCO) 2015 Cotillas.pdf Lighting Biomass + Yecla Swimming July 2014 - December INFO technical support 9 ER Energy CALFRICA, S.L. -

Characterization of Leachate from Different Landfills Sites of Morocco and Spain: a Comparative Study
European Scientific Journal Jume 2019 edition Vol.15, No.18 ISSN: 1857 – 7881 (Print) e - ISSN 1857- 7431 Characterization of Leachate from Different Landfills Sites of Morocco and Spain: A Comparative Study El Bied Oumaima, Bioscience Laboratory, University of science and technology Mohammedia, Hassan II University of Casablanca, Morocco Research group GARSA, Universidad Politécnica de Cartagena, Spain Angel Faz Cano, Jose Alberto Acosta Aviles, Research group GARSA, Universidad Politécnica de Cartagena, Spain Taoufiq Fechtali, Bioscience Laboratory, University of science and technology Mohammedia, Hassan II University of Casablanca, Morocco Doi: 10.19044/esj.2019.v15n18p183 URL:http://dx.doi.org/10.19044/esj.2019.v15n18p183 Abstract The socio-economic activities in Morocco and Spain as well as all the other countries around the world involving population growth and changes in consumption behavior have generated a substantial and important solid waste production. The decomposition of waste by microorganisms in landfills generates soluble compounds, which under the leaching action and water infiltration meteorites come to mix together forming “leachate juices”. Its composition varies widely depending on the age of the landfill and the type of waste it contains. The latter usually contains dissolved and suspended material. This study aims to characterize the physicochemical properties and evaluate the mineral and organic compounds of different leachates. It is worthy to note that this physicochemical characterization is arbitrary because those landfills will soon be equipped with an elimination center and treatment. The following objectives of this paper have been set for this work; on one hand, to determine the qualitative characteristics aspects of leachates that are essential for characterizing the pollutant load and, thus, estimating the risks that these leachates pose to the water quality of the surrounding groundwater. -

Región De Murcia Religious and Cultural Tourism
RELIGI US REGIÓN DE MURCIA RELIGIOUS AND CULTURAL TOURISM A JUBILEE 1 CITY PERPETUAL 1 JUBILEE YEAR RELIGIOUS FESTIVALS OF INTERNATIONAL TOURIST 4 INTEREST DAYS OF SUNSHINE 300 PER YEAR DEGREES (OUR AVERAGE 19 TEMPERATURE) MAKES YOU HAPPY MURCIA REGIÓN DE MURCIA PLACES OF PILGRIMAGE To explore the Region of Murcia, keep your feet on the ground. With each step, you'll experience emotions that elevate your spirit beyond the earthly. The Region of Murcia is a focal point of Christianity, evidenced by Pope John Paul II granting the privilege to celebrate the Jubilee Year In Perpetuum in Caravaca de la Cruz every 7 years since 2003. Thus, Caravaca became the fifth city in the world to celebrate the Perpetual Jubilee, together with Santiago de Composte- la, Santo Toribio de Liebana, Rome and Jerusalem, the next taking place in 2017. The religious tradition of the Region of Murcia not only dwells in every church and basilica: worship and fervour are rooted in every corner, town and city. Discover beautiful worship sites, places of pilgrimage, legends, religious festivals and heritage of incalculable value. RELIGIOUS AND CULTURAL CARAVACA DE LA CRUZ Holy Jubilee Year + Info www.turismocaravaca.org www.caminodelacruz.es Caravaca de la Cruz is a city located in a border enclave, a crossroads between the Region of Murcia and Granada. Iberians, Romans and Muslims passed through a community settled around its castle, which, although of Arab origin, was guarded by the Knights Templar and subsequently by the Order of Santiago. Caravaca is essentially the City of the Cross. According to legend, in 1232 the Moorish king Abu Zeid converted to Christianity when he witnessed two angels descending from heaven carrying a cross so that a priest imprisoned in the castle could say mass. -

Patrimonio Y Paisaje Cultural Del Agua En El Valle De Ricote (Murcia) Heritage and Cultural Landscapes of Water in the Ricote Valley (Murcia)
e-rph Concepto | Estudios | María Griñán M., Juan C. Trigueros M. Concepto| Estudios Patrimonio y paisaje cultural del agua en el Valle de Ricote (Murcia) Heritage and cultural landscapes of water in the Ricote Valley (Murcia) María Griñán Montealegre 5 Doctora en Historia del Arte. Profesora Titular en el Departamento Historia del Arte Juan Carlos Trigueros Molina Doctor en Historia del Arte. Universidad de Murcia Resumen El Valle de Ricote constituye un paisaje complejo vertebrado por el curso fluvial del río Segura en el Sudeste peninsular que se ha convertido en un espacio singular reflejo de la huella cultural de más de dos milenios, por lo que se debería proteger a través de un Plan Especial del Paisaje del Agua. Ello afectaría en diferente grado a los ocho municipios que componen el también llamado Valle Morisco por constituir uno de los últimos reductos de esta minoría étnica en la Península Ibérica hasta bien entrada la Edad Moderna. Este trabajo pretende aportar nuevos datos sobre un territorio en el que orografía, administración e historia le han otorgado un valor cultural y paisajístico protagonizado además de por una serie de construcciones, estructuras y artilugios hidráulicos, por ramblas y humedales, por tradiciones y sistemas de organización y gobernanza que hasta la fecha han quedado en un segundo plano y que resultan imprescindibles para comprender la pervivencia de la agricultura y regadíos tradicionales. Es el caso del papel que la Orden e-rph nº 22, junio 2018, pp. 5-36 e-rph Concepto | Estudios | María Griñán M., Juan C. Trigueros M. Militar de Santiago jugó en la trasformación del espacio y la forma de gobierno del agua, sistemas que se han adaptado perviviendo hasta la actualidad, y que a pesar de su importancia en la evolución del territorio son hoy poco conocidos no sólo para sus habitantes sino también para la administración local y regional. -

Actualidad Leader 28 Las Norias Del Valle Morisco
Vega del Segura (Murcia) Actualidad Leader 28 Las norias del valle morisco El río Segura ve una comarca s c. iastes pa sticos en la que altern zonas de fértite:. as con las áreas semidesérticas. ,a vega, los pueblc:- mbarán, Blanca, Ricote, Ojós, Ulea, ViRaL. eva, Archena, Ceutí, _,rquí y Alguazas, delimitan el territorio acogido al Programa LEADER, El Segura ha sido tradicionalmente el dina- denado un grave problema de retroceso econó- mizador de la economía de la comarca. En sus mico en la comarca, antes puntera en el desa- riberas han crecido desde antiguo las huertas y rrollo regional y que poco a poco se convierte los frutales y se han desarrollado las industrias en "zona dormitorio" de los grandes núcleos de manipulación y transfor- cercanos, Molina de Segura y Murcia. Hoy, la mación -especialmente con- Vega del Segura es la zona con menor renta de serveras- asociadas a las acti- la región. vidades agrícolas. La agricultura es, pues, la base económica sobre la que El LEADER comarcal colabora descansan el resto de las acti- vidades de la zona. La dimen- en la rehabilitación de las sión de las explotaciones agrarias es reducida: un 93% norias del Segura y en la tiene menos de 5 Ha. y entre el 92 y el 95% de aquellas no restauración paisajística del río tienen por sí solas viabilidad económica. El tejido indus- Otros indicadores ilustran en la misma trial es débil, con escaso nivel dirección: la tasa de analfabetismo es superior a- de inversiones y baja cualifi- la de la región en más de 5 puntos, 8 en el caso cación profesional de los tra- de las mujeres. -

VI+Congreso.Pdf
ASOCIACIÓN DE CRONISTAS OFICIALES DE LA REGIÓN DE MURCIA AYUNTAMIENTO DE ARCHENA ARCHENA 550 AÑOS DE HISTORIA Manuel Enrique Medina Tornero (Coord.) VI Congreso Regional de la Asociación de Cronistas de Murcia (Archena, 16 de Marzo de 2013) Edita: Ayuntamiento de Archena. Asociación de Cronistas Oficiales de la Región de Murcia. Diseño de portada y maquetación: Jesús Alcolea Martínez. Coordinación: Manuel Enrique Medina Tornero. Depósito Legal: MU-1214-2013 Nº ISBN: 978-84-616-7347-6 Imprime: Imprenta Garrido - Telf.: 679 956 316 E-mail: [email protected] ÍNDICE SALUTACIÓN DE LA ALCALDESA 9 Patricia Fernández López PRÓLOGO 11 José Antonio Melgares Guerrero DISCURSO DEL PRESIDENTE DE RAECO 15 Antonio Luis Galiano Pérez La Orden de san Juan de Jerusalén y Archena: concesión de carta de población en 1462 17 Manuel Enrique Medina Tornero Las bandas de música de Archena y valle de Ricote 47 Ricardo Montes Bernárdez Carmen Terry y el parque de la marquesa. Ulea (Murcia) 57 Ricardo Montes Bernárdez La implantación del retiro obrero en Archena, Lorquí, Ceutí, Alguazas, Cotillas, Molina y Fortuna. 67 José Antonio Marín Mateos Archena, san Javier y el mar menor 77 Miguel Gallego Zapata Pedro de Llamas y Molina (1737-1822). Esbozo biográfico de un militar y político del antiguo régimen 83 Dimas Ortega López 550 aniversario de la carta puebla de Archena y 572 de Puebla de Soto, con san Antón de la escudera al fondo 93 Juan José Franco Manzano 5 ARCHENA. 550 AÑOS DE HISTORIA Un curioso documento del siglo XVIII de la villa de Mula -

De Nombres, Casas Y Habitantes En El Valle De Ricote a Mediados Del Siglo XIX
De nombres, casas y habitantes en el Valle de Ricote a mediados del siglo XIX Ricardo Montes Bernárdez Doctor en Arqueología e Historia Antigua Académico C. de la Real de Alfonso X En torno a 1860 el Boletín Oficial de la Provincia de Murcia publicaba una serie de datos relativos al valle de Ricote en cuanto a su población, pedanías, caseríos y número de viviendas que venían a completar el trabajo de Pascual Madoz publicado en Madrid en 1850. Con esta información podemos hoy aproximarnos a ciertos aspectos de la vida cotidiana de agricultores, pastores e incluso algunos viajeros que todavía conocieron casas y parajes, hoy desaparecidos, pero presentes en el recuerdo y la memoria colectiva de las gentes de este bellísimo rincón de la geografía murciana. En cambio, otros sitios como Cañada del Rey, Oya del Comendador, Rincón del Comendador, Cara, Fontanilla, Ramel, Sobarbe..., si se han perdido irreparablemente; eran mencionados en 1755 en el Catastro del Marqués de la Ensenada y aparecían clasificados como lugares de cultivo cuyo número llegaba a 477 en todo el Valle (García:2000:48). En alguno de estos enclaves se estableció casa de labranza y hasta caserío. De todos ellos, todavía en 1860 pervivían algunos, pues bien, a estos últimos vamos a pasar revista en las páginas siguientes. Abarán Alrededor de 1846 contaba con 430 casas que constituían el casco urbano. Se hallaban dominadas por una ermita, en la cumbre del cerro, reconstruida entre 1834 y 1839 y dedicada a los santos Cosme y Damián. El término albergaba entonces a 2.455 habitantes. -

An Atlas of Commercial Geography
IO?-5 AN ATLAS OF COMMERCIAL GEOGRAPHY % % "i % ¥ .i. J- >- %t ST'' .T. CAMBRIDGE ^ UNIVERSITY PRESS a^^^^^^^^^^^ggSgfjSjSjSigHiasH^^^^^^^a^^^^^^^^^li^gigaa Dtate Collese of iKgricuUure m Cornell ^Hnibersitp Stfjaca, i5. g. ILibrarp """^'^'>y HF 1023.A4°'"^" Library llMl!™™,f,,°'<=°'"'"ei-cialc Cornell University Library V, The original of this book is in the Cornell University Library. There are no known copyright restrictions in the United States on the use of the text. http://www.archive.org/details/cu31924013803618 AN ATLAS OF COMMERCIAL GEOGRAPHY ; INTRODUCTION THIS Atlas is specially intended to be used with the for the tropics, but is useful as indicating the significance Elementary Commercial Geography published by the of the great lowland areas which characterise the tem- Cambridge University Press, but it is hoped that such perate zones. a series of maps, illustrating the elementary facts of eco- In the tropics, as mentioned, climatic conditions nomic geography, will be of general use to students. The favour the gi'owth of population rather on the highlands work falls into two broad divisions ; the first containing than the lowlands; but the difficulties of communication maps presenting facts on the world-scale, on which the retard the commercial development of the former areas. teaching of principles may be based ; the second giving a P. 4. In using these maps, it should first be made consistent series of maps for each continent, sufficiently clear that the temperatures shown are reduced to sea- detailed, it is hoped, to be of use for regional stud}'. level, and some idea of the effect of altitude on tempera- The object of this Introduction is to indicate a logical ture given—in general terms, that the latter diminishes method of study, by linking facts together in a natural by 1°F. -

Consolidation of Aedes Albopictus Surveillance Program in the Autonomous Community of the Region of Murcia, Spain
International Journal of Environmental Research and Public Health Article Consolidation of Aedes albopictus Surveillance Program in the Autonomous Community of the Region of Murcia, Spain Francisco Collantes 1,* , Manuel José Méndez 2, Caridad Soto-Castejón 2 and Eva María Muelas 2 1 Departamento de Zoología y Antropología Física, Facultad de Biología, Universidad de Murcia, 30100 Murcia, Spain 2 Servicio de Sanidad Ambiental, Consejería de Salud de la Región de Murcia, 30008 Murcia, Spain; [email protected] (M.J.M.); [email protected] (C.S.-C.); [email protected] (E.M.M.) * Correspondence: [email protected]; Tel.: +34-868-883-939 Received: 19 April 2020; Accepted: 10 June 2020; Published: 11 June 2020 Abstract: Background: Due to the Spanish legal framework, the national program for vector-borne diseases results from the agreement between national and regional governments, and it is the basis for the development of the regional programs, which should include the regional entomological surveillance program. Aedes albopictus was recorded for the first time in the Region of Murcia, in 2011. It gave rise to a new epidemiological scenario due to the presence of a competent vector of several arboviruses, which resulted in autochthonous cases of dengue in 2018. Methods: 40 out of 45 municipalities participated in the regional entomological surveillance program, and 266 sampling points were established, with two ovitraps at each site as pseudo-replications. The study period was from April 16th to November 26th, with bi-weekly sample collections: 16 regional samplings were carried out. Results: Regional participation was high, and data loss was low (1.26%). -

Key to Symbols
WHERE AM I TODAY? N-344 ROADS MOTORWAY / DUAL CARRIAGEWAY NATIONAL DISTRICT LOCAL OTHER ROADS NATURAL PARKS & PROTECTED AREAS REGIONAL PARKS CETE ALBA OF P PROTECTED LANDSCAPES E R C O IN V NATURAL AREAS V O IN R C NATURE RESERVES P E O F A L I C A N T E Alicante El Altet Airport P R O V IN C E O F G R A N Alicante El Altet Airport A D A (under construction) RM-E11 RM-C22 MEDITERRANEAN SEA P R O V IN C E O F A LM ER ÍA KEY TO SYMBOLS TOURIST OFFICE CAMP SITE BALNEOTHERAPY SPA AIRPORT MARINA SEA SPORTS RESORT SITE OF HISTORICAL / ARTISTIC INTEREST MUSEUM CASTLE ARCHAEOLOGICAL AREA WORLD HERITAGE ROCK ART ROMAN THEATRE WINERY NAUTICAL SPORTS ADVENTURE SPORTS GOLF THALASSOTHERAPY CENTRE PARADOR VISITOR CENTRE GREEN ROUTE GREEN PATH TODAY I FEEL LIKE A FISH TODAY I TODAY I FEEL CURIOUS LA MANGA & ÁGUILAS MAZARRÓN FEEL LIKE CARTAGENA LORCA CARAVACA DE MURCIA MAR MENOR GOLF LA CRUZ www.marmenor.net www.aguilas.es www.mazarron.es www.murciaturistica.es www.cartagenapuertodeculturas.com www.lorcatallerdeltiempo.es www.caravacajubilar.com www.murciaciudad.com Footsteps in the sand Emblematic buildings Magical landscapes Golf & sea Punic Cartagena Historical adventure Jubilee City Baroque route Discover small deserted coves and the A walk through Águilas's old town will By the extensive Bolnuevo beach, the Play a few holes at any of the following Cartagena Port of Cultures invites you Go on an adventure through time at the Caravaca de la Cruz is the fifth city in the The Cathedral (14th-18th C) features landscapes of Calblanque Natural Park.