Trigonometry Outline
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Division by Zero Calculus and Singular Integrals
Proceedings of International Conference on Mechanical, Electrical and Medical Intelligent System 2017 Division by Zero Calculus and Singular Integrals Tsutomu Matsuura1, a and Saburou Saitoh2,b 1Faculty of Science and Technology, Gunma University, 1-5-1 Tenjin-cho, Kiryu 376-8515, Japan 2Institute of Reproducing Kernels, Kawauchi-cho, 5-1648-16, Kiryu 376-0041, Japan [email protected], [email protected] Keywords: division by zero, point at infinity, singularity, Laurent expansion, Hadamard finite part Abstract. In this paper, we will introduce the formulas log 0= log ∞= 0 (not as limiting values) in the meaning of the one point compactification of Aleksandrov and their fundamental applications, and we will also examine the relationship between Laurent expansion and the division by zero. Based on those examinations we give the interpretation for the Hadamard finite part of singular integrals by means of the division by zero calculus. In particular, we will know that the division by zero is our elementary and fundamental mathematics. 1. Introduction By a natural extension of the fractions b (1) a for any complex numbers a and b , we found the simple and beautiful result, for any complex number b b = 0, (2) 0 incidentally in [1] by the Tikhonov regularization for the Hadamard product inversions for matrices and we discussed their properties and gave several physical interpretations on the general fractions in [2] for the case of real numbers. The result is very special case for general fractional functions in [3]. The division by zero has a long and mysterious story over the world (see, for example, H. -

Refresher Course Content
Calculus I Refresher Course Content 4. Exponential and Logarithmic Functions Section 4.1: Exponential Functions Section 4.2: Logarithmic Functions Section 4.3: Properties of Logarithms Section 4.4: Exponential and Logarithmic Equations Section 4.5: Exponential Growth and Decay; Modeling Data 5. Trigonometric Functions Section 5.1: Angles and Radian Measure Section 5.2: Right Triangle Trigonometry Section 5.3: Trigonometric Functions of Any Angle Section 5.4: Trigonometric Functions of Real Numbers; Periodic Functions Section 5.5: Graphs of Sine and Cosine Functions Section 5.6: Graphs of Other Trigonometric Functions Section 5.7: Inverse Trigonometric Functions Section 5.8: Applications of Trigonometric Functions 6. Analytic Trigonometry Section 6.1: Verifying Trigonometric Identities Section 6.2: Sum and Difference Formulas Section 6.3: Double-Angle, Power-Reducing, and Half-Angle Formulas Section 6.4: Product-to-Sum and Sum-to-Product Formulas Section 6.5: Trigonometric Equations 7. Additional Topics in Trigonometry Section 7.1: The Law of Sines Section 7.2: The Law of Cosines Section 7.3: Polar Coordinates Section 7.4: Graphs of Polar Equations Section 7.5: Complex Numbers in Polar Form; DeMoivre’s Theorem Section 7.6: Vectors Section 7.7: The Dot Product 8. Systems of Equations and Inequalities (partially included) Section 8.1: Systems of Linear Equations in Two Variables Section 8.2: Systems of Linear Equations in Three Variables Section 8.3: Partial Fractions Section 8.4: Systems of Nonlinear Equations in Two Variables Section 8.5: Systems of Inequalities Section 8.6: Linear Programming 10. Conic Sections and Analytic Geometry (partially included) Section 10.1: The Ellipse Section 10.2: The Hyperbola Section 10.3: The Parabola Section 10.4: Rotation of Axes Section 10.5: Parametric Equations Section 10.6: Conic Sections in Polar Coordinates 11. -
Algebra/Geometry/Trigonometry App Samples
Algebra/Geometry/Trigonometry App Samples Holt McDougal Algebra 1 HMH Fuse: Algebra 1- HMH Fuse is the first core K-12 education solution developed exclusively for the iPad. The portability of a complete classroom course on an iPad enables students to learn in the classroom, on the bus, or at home—anytime, anywhere—with engaging content that provides an individually-tailored learning experience. Students and educators using HMH Fuse: will benefit from: •Instructional videos that teach or re-teach all key concepts •Math Motion is a step-by-step interactive demonstration that displays the process to solve complex equations •Homework Help provides at-home support for intricate problems by providing hints for each step in the solution •Vocabulary support throughout with links to a complete glossary that includes audio definitions •Tips, hints, and links that enable students to acquire the help they need to understand the lessons every step of the way •Quizzes that assess student’s skills before they begin a concept and at strategic points throughout the chapters. Instant, automatic grading of quizzes lets students know exactly how they have performed •Immediate assessment results sent to teachers so they can better differentiate instruction. Sample- Cost is Free, Complete App price- $59.99 Holt McDougal HMH Fuse: Geometry- Following our popular HMH Fuse: Algebra 1 app, HMH Fuse: Geometry is the newest offering in the HMH Fuse series. HMH Fuse: Geometry will allow you a sneak peek at the future of mobile geometry curriculum and includes a FREE sample chapter. HMH Fuse is the first core K-12 education solution developed exclusively for the iPad. -
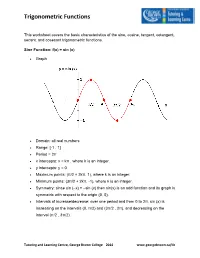
Trigonometric Functions
Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer. -

Lecture 5: Complex Logarithm and Trigonometric Functions
LECTURE 5: COMPLEX LOGARITHM AND TRIGONOMETRIC FUNCTIONS Let C∗ = C \{0}. Recall that exp : C → C∗ is surjective (onto), that is, given w ∈ C∗ with w = ρ(cos φ + i sin φ), ρ = |w|, φ = Arg w we have ez = w where z = ln ρ + iφ (ln stands for the real log) Since exponential is not injective (one one) it does not make sense to talk about the inverse of this function. However, we also know that exp : H → C∗ is bijective. So, what is the inverse of this function? Well, that is the logarithm. We start with a general definition Definition 1. For z ∈ C∗ we define log z = ln |z| + i argz. Here ln |z| stands for the real logarithm of |z|. Since argz = Argz + 2kπ, k ∈ Z it follows that log z is not well defined as a function (it is multivalued), which is something we find difficult to handle. It is time for another definition. Definition 2. For z ∈ C∗ the principal value of the logarithm is defined as Log z = ln |z| + i Argz. Thus the connection between the two definitions is Log z + 2kπ = log z for some k ∈ Z. Also note that Log : C∗ → H is well defined (now it is single valued). Remark: We have the following observations to make, (1) If z 6= 0 then eLog z = eln |z|+i Argz = z (What about Log (ez)?). (2) Suppose x is a positive real number then Log x = ln x + i Argx = ln x (for positive real numbers we do not get anything new). -

An Appreciation of Euler's Formula
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 1 Article 17 An Appreciation of Euler's Formula Caleb Larson North Dakota State University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Larson, Caleb (2017) "An Appreciation of Euler's Formula," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 1 , Article 17. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss1/17 Rose- Hulman Undergraduate Mathematics Journal an appreciation of euler's formula Caleb Larson a Volume 18, No. 1, Spring 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 [email protected] a scholar.rose-hulman.edu/rhumj North Dakota State University Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 1, Spring 2017 an appreciation of euler's formula Caleb Larson Abstract. For many mathematicians, a certain characteristic about an area of mathematics will lure him/her to study that area further. That characteristic might be an interesting conclusion, an intricate implication, or an appreciation of the impact that the area has upon mathematics. The particular area that we will be exploring is Euler's Formula, eix = cos x + i sin x, and as a result, Euler's Identity, eiπ + 1 = 0. Throughout this paper, we will develop an appreciation for Euler's Formula as it combines the seemingly unrelated exponential functions, imaginary numbers, and trigonometric functions into a single formula. To appreciate and further understand Euler's Formula, we will give attention to the individual aspects of the formula, and develop the necessary tools to prove it. -

Unit Circle Trigonometry
UNIT CIRCLE TRIGONOMETRY The Unit Circle is the circle centered at the origin with radius 1 unit (hence, the “unit” circle). The equation of this circle is xy22+ =1. A diagram of the unit circle is shown below: y xy22+ = 1 1 x -2 -1 1 2 -1 -2 We have previously applied trigonometry to triangles that were drawn with no reference to any coordinate system. Because the radius of the unit circle is 1, we will see that it provides a convenient framework within which we can apply trigonometry to the coordinate plane. Drawing Angles in Standard Position We will first learn how angles are drawn within the coordinate plane. An angle is said to be in standard position if the vertex of the angle is at (0, 0) and the initial side of the angle lies along the positive x-axis. If the angle measure is positive, then the angle has been created by a counterclockwise rotation from the initial to the terminal side. If the angle measure is negative, then the angle has been created by a clockwise rotation from the initial to the terminal side. θ in standard position, where θ is positive: θ in standard position, where θ is negative: y y Terminal side θ Initial side x x Initial side θ Terminal side Unit Circle Trigonometry Drawing Angles in Standard Position Examples The following angles are drawn in standard position: y y 1. θ = 40D 2. θ =160D θ θ x x y 3. θ =−320D Notice that the terminal sides in examples 1 and 3 are in the same position, but they do not represent the same angle (because x the amount and direction of the rotation θ in each is different). -

Developing Creative Thinking in Mathematics: Trigonometry
Secondary Mathematics Developing creative thinking in mathematics: trigonometry Teacher Education through School-based Support in India www.TESS-India.edu.in http://creativecommons.org/licenses/ TESS-India (Teacher Education through School-based Support) aims to improve the classroom practices of elementary and secondary teachers in India through the provision of Open Educational Resources (OERs) to support teachers in developing student-centred, participatory approaches. The TESS-India OERs provide teachers with a companion to the school textbook. They offer activities for teachers to try out in their classrooms with their students, together with case studies showing how other teachers have taught the topic and linked resources to support teachers in developing their lesson plans and subject knowledge. TESS-India OERs have been collaboratively written by Indian and international authors to address Indian curriculum and contexts and are available for online and print use (http://www.tess-india.edu.in/). The OERs are available in several versions, appropriate for each participating Indian state and users are invited to adapt and localise the OERs further to meet local needs and contexts. TESS-India is led by The Open University UK and funded by UK aid from the UK government. Video resources Some of the activities in this unit are accompanied by the following icon: . This indicates that you will find it helpful to view the TESS-India video resources for the specified pedagogic theme. The TESS-India video resources illustrate key pedagogic techniques in a range of classroom contexts in India. We hope they will inspire you to experiment with similar practices. They are intended to complement and enhance your experience of working through the text-based units, but are not integral to them should you be unable to access them. -

Division by Zero in Logic and Computing Jan Bergstra
Division by Zero in Logic and Computing Jan Bergstra To cite this version: Jan Bergstra. Division by Zero in Logic and Computing. 2021. hal-03184956v2 HAL Id: hal-03184956 https://hal.archives-ouvertes.fr/hal-03184956v2 Preprint submitted on 19 Apr 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. DIVISION BY ZERO IN LOGIC AND COMPUTING JAN A. BERGSTRA Abstract. The phenomenon of division by zero is considered from the per- spectives of logic and informatics respectively. Division rather than multi- plicative inverse is taken as the point of departure. A classification of views on division by zero is proposed: principled, physics based principled, quasi- principled, curiosity driven, pragmatic, and ad hoc. A survey is provided of different perspectives on the value of 1=0 with for each view an assessment view from the perspectives of logic and computing. No attempt is made to survey the long and diverse history of the subject. 1. Introduction In the context of rational numbers the constants 0 and 1 and the operations of addition ( + ) and subtraction ( − ) as well as multiplication ( · ) and division ( = ) play a key role. When starting with a binary primitive for subtraction unary opposite is an abbreviation as follows: −x = 0 − x, and given a two-place division function unary inverse is an abbreviation as follows: x−1 = 1=x. -

IEEE Standard 754 for Binary Floating-Point Arithmetic
Work in Progress: Lecture Notes on the Status of IEEE 754 October 1, 1997 3:36 am Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic Prof. W. Kahan Elect. Eng. & Computer Science University of California Berkeley CA 94720-1776 Introduction: Twenty years ago anarchy threatened floating-point arithmetic. Over a dozen commercially significant arithmetics boasted diverse wordsizes, precisions, rounding procedures and over/underflow behaviors, and more were in the works. “Portable” software intended to reconcile that numerical diversity had become unbearably costly to develop. Thirteen years ago, when IEEE 754 became official, major microprocessor manufacturers had already adopted it despite the challenge it posed to implementors. With unprecedented altruism, hardware designers had risen to its challenge in the belief that they would ease and encourage a vast burgeoning of numerical software. They did succeed to a considerable extent. Anyway, rounding anomalies that preoccupied all of us in the 1970s afflict only CRAY X-MPs — J90s now. Now atrophy threatens features of IEEE 754 caught in a vicious circle: Those features lack support in programming languages and compilers, so those features are mishandled and/or practically unusable, so those features are little known and less in demand, and so those features lack support in programming languages and compilers. To help break that circle, those features are discussed in these notes under the following headings: Representable Numbers, Normal and Subnormal, Infinite -

Trigonometric Functions
Hy po e te t n C i u s se o b a p p O θ A c B Adjacent Math 1060 ~ Trigonometry 4 The Six Trigonometric Functions Learning Objectives In this section you will: • Determine the values of the six trigonometric functions from the coordinates of a point on the Unit Circle. • Learn and apply the reciprocal and quotient identities. • Learn and apply the Generalized Reference Angle Theorem. • Find angles that satisfy trigonometric function equations. The Trigonometric Functions In addition to the sine and cosine functions, there are four more. Trigonometric Functions: y Ex 1: Assume � is in this picture. P(cos(�), sin(�)) Find the six trigonometric functions of �. x 1 1 Ex 2: Determine the tangent values for the first quadrant and each of the quadrant angles on this Unit Circle. Reciprocal and Quotient Identities Ex 3: Find the indicated value, if it exists. a) sec 30º b) csc c) cot (2) d) tan �, where � is any angle coterminal with 270 º. e) cos �, where csc � = -2 and < � < . f) sin �, where tan � = and � is in Q III. 2 Generalized Reference Angle Theorem The values of the trigonometric functions of an angle, if they exist, are the same, up to a sign, as the corresponding trigonometric functions of the reference angle. More specifically, if α is the reference angle for θ, then cos θ = ± cos α, sin θ = ± sin α. The sign, + or –, is determined by the quadrant in which the terminal side of θ lies. Ex 4: Determine the reference angle for each of these. Then state the cosine and sine and tangent of each. -

4.2 – Trigonometric Functions: the Unit Circle
Warm Up Warm Up 1 The hypotenuse of a 45◦ − 45◦ − 90◦ triangle is 1 unit in length. What is the measure of each of the other two sides of the triangle? 2 The hypotenuse of a 30◦ − 60◦ − 90◦ triangle is 1 unit in length. What is the measure of each of the other two sides of the triangle? Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 1 / 27 4.2 { Trigonometric Functions: The Unit Circle Pre-Calculus Mr. Niedert Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 2 / 27 2 Trigonometric Functions 3 Domain and Period of Sine and Cosine 4 Evaluating Trigonometric Functions with a Calculator 4.2 { Trigonometric Functions: The Unit Circle 1 The Unit Circle Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 3 / 27 3 Domain and Period of Sine and Cosine 4 Evaluating Trigonometric Functions with a Calculator 4.2 { Trigonometric Functions: The Unit Circle 1 The Unit Circle 2 Trigonometric Functions Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 3 / 27 4 Evaluating Trigonometric Functions with a Calculator 4.2 { Trigonometric Functions: The Unit Circle 1 The Unit Circle 2 Trigonometric Functions 3 Domain and Period of Sine and Cosine Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 3 / 27 4.2 { Trigonometric Functions: The Unit Circle 1 The Unit Circle 2 Trigonometric Functions 3 Domain and Period of Sine and Cosine 4 Evaluating Trigonometric Functions with a Calculator Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr.