The Endgame in Poker
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

MJ GONZALES: Ankush Mandavia Talks DANIEL NEGREANU’S About Triumphant Return to Live COACH SEEKS out Tournament Circuit
www.CardPlayer.com Vol. 34/No. 9 April 21, 2021 MJ GONZALES: Ankush Mandavia Talks DANIEL NEGREANU’S About Triumphant Return To Live COACH SEEKS OUT Tournament Circuit HEADS-UP ACTION Twitch Streamer Vanessa Kade Gets Last OF HIS OWN Laugh, Wins Sunday High-Stakes Pro Talks Upcoming Million For $1.5M $3M Freezeout, Private Games, And New Coaching Platform Tournament Strategy: Position And Having The Lead PLAYER_34_08_Cover.indd 1 3/31/21 9:29 AM PLAYER_08_GlobalPoker_DT.indd 2 3/16/21 9:39 AM PLAYER_08_GlobalPoker_DT.indd 3 3/16/21 9:39 AM Masthead - Card Player Vol. 34/No. 9 PUBLISHERS Barry Shulman | Jeff Shulman Editorial Corporate Office EDITORIAL DIRECTOR Julio Rodriguez 6940 O’Bannon Drive TOURNAMENT CONTENT MANAGER Erik Fast Las Vegas, Nevada 89117 ONLINE CONTENT MANAGER Steve Schult (702) 871-1720 Art [email protected] ART DIRECTOR Wendy McIntosh Subscriptions/Renewals 1-866-LVPOKER Website And Internet Services (1-866-587-6537) CHIEF TECHNOLOGY OFFICER Jaran Hardman PO Box 434 DATA COORDINATOR Morgan Young Congers, NY 10920-0434 Sales [email protected] ADVERTISING MANAGER Mary Hurbi Advertising Information NATIONAL SALES MANAGER Barbara Rogers [email protected] LAS VEGAS AND COLORADO SALES REPRESENTATIVE (702) 856-2206 Rich Korbin Distribution Information cardplayer Media LLC [email protected] CHAIRMAN AND CEO Barry Shulman PRESIDENT AND COO Jeff Shulman Results GENERAL COUNSEL Allyn Jaffrey Shulman [email protected] VP INTL. BUSINESS DEVELOPMENT Dominik Karelus CONTROLLER Mary Hurbi Schedules FACILITIES MANAGER Jody Ivener [email protected] Follow us www.facebook.com/cardplayer @CardPlayerMedia Card Player (ISSN 1089-2044) is published biweekly by Card Player Media LLC, 6940 O’Bannon Drive, Las Vegas, NV 89117. -

Download the Full Tilt Poker Strategy Guide
The Full Tilt Poker Strategy Guide: Tournament Edition, Andy Bloch, Richard Brodie, Chris Ferguson, Ted Forrest, Rafe Furst, Phil Gordon, David Grey, Howard Lederer, Mike Matusow, Huckleberry Seed, Gavin Smith, Keith Sexton, Grand Central Publishing, 2007, 0446196916, 9780446196918, . The professionals of Full Tilt Poker include the best and most famous poker players in the world. Their accomplishments are unparalleled, with countless World Series of Poker and World Poker Tour championships to their names and well in excess of $100 million in winnings in private games. Now, this group of poker legends has banded together to create THE FULL TILT POKER STRATEGY GUIDE, which will stand as an instant classic of the genre and is sure to become the industry standard.. DOWNLOAD HERE http://bit.ly/1eusMy2 Play Poker Like the Pros , Phil Hellmuth, Jr., Mar 17, 2009, Games, 416 pages. In Play Poker Like the Pros, poker master Phil Hellmuth, Jr., demonstrates exactly how to play and win -- even if you have never picked up a deck of cards -- the modern games .... Killer Poker by the Numbers The Mathematical Edge for Winning Play, Tony Guerrera, Dec 26, 2006, Games, 310 pages. The first and only poker book to thoroughly cover the mathematical concepts behind every hand of poker and do it in an easy and accessible manner. At its root poker is a .... Poker The Real Deal, Phil Gordon, Jonathan Grotenstein, Oct 7, 2004, Games, 304 pages. Like a secret society, poker has its own language and customs -- its own governing logic and rules of etiquette that the uninitiated may find intimidating. -

ISA-GUIDE Täglicher Newsletter Hallo Newsletter-Abonnent! Hier Ist Die Tägliche Zusammenfassung Neuer Beiträge Auf ISA- GUIDE
ISA-GUIDE Täglicher Newsletter Hallo Newsletter-Abonnent! Hier ist die tägliche Zusammenfassung neuer Beiträge auf ISA- GUIDE. ISA-CASINOS Negreanu verpasst siebtes Bracelet Die Bracelet-Durststrecke von Daniel Negreanu geht weiter. Die Poker-Legende muss sich beim Seven Card Stud im Heads-Up einem US-Amerikaner geschlagen geben. Poker-Legende Daniel Negreanu hat bei der WSOP 2019 nur knapp sein siebtes Siegerarmband bei einer Poker-WM in seinem Wohnort Las Vegas verpasst. 2019 World Series of Poker: Dan “centrfieldr’ Lupo gewinnt Event #46 Heute Nacht endete Event #46, das $500 WSOP.com ONLINE No- Limit Hold’em Turbo Deepstack Turnier der 2019 World Series of Poker. An den Start gingen 1181 Spieler, alle mit der Hoffnung auf das begehrte Schmuckstück. 2019 World Series of Poker: John Hennigan gewinnt Bracelet Nr.6 bei Event #41 Heute Vormittag ging auch Event #41, die $10,000 Seven Card Stud Championship der 2019 World Series of Poker zu Ende. An den Start gingen 88 Spieler, darunter Scott Seiver, Eli Elezra, Scott Clements, Greg Mueller, Michael Mizrachi, Tom Koral, Max Pescatori, Daniel Negreanu, David „ODB“ Baker, Frank Kassela, John Monnette, Brian Hastings und Paul Volpe. 2019 World Series of Poker: Ismael Bojang gewinnt Event #40 Heute Morgen ging auch Event #40, das $1,500 Pot-Limit Omaha Turnier der 2019 World Series of Poker zu Ende. An den Start gingen 1216 Spieler, darunter Steve Sung, James Little, Norbert Szecsi, Anton Wigg, Erik Seidel, Mike Matusow, Barny Boatman, Matt Glantz, Kenny Hallaert, Ismael Bojang, Brock Parker, Jan Collado, Varahram Vardjavand, Tobias Peters, Tom Marchese und Sven Reichardt. -

MOTION to Dismiss. Document Filed by Andrew Bloch, Allen Cunningham, Christopher Ferguson, Filco, Ltd., Jennifer Harman-Traniel
Segal et al v. Bitar et al Doc. 62 IN THE UNITED STATES DISTRICT COURT FOR THE SOUTHERN DISTRICT OF NEW YORK __________________________________________ ) STEVEN SEGAL, NICK HAMMER, ROBIN ) HOUGDAHL, and TODD TERRY, on behalf of ) themselves and all other similarly situated ) ) Plaintiffs, ) Civil Action No.: 11-CV-4521 (LBS) ) v. ) ) RAYMOND BITAR; NELSON BURTNICK; ) FULL TILT POKER, LTD.; TILTWARE, LLC; ) VANTAGE, LTD; FILCO, LTD.; KOLYMA ) CORP. A.V.V.; POCKET KINGS LTD.; ) POCKET KINGS CONSULTING LTD.; ) RANSTON LTD.; MAIL MEDIA LTD.; ) HOWARD LEDERER; PHILLIP IVEY JR.; ) CHRISTOPHER FERGUSON; JOHNSON ) JUANDA; JENNIFER HARMAN-TRANIELLO; ) PHILLIP GORDON; ERICK LINDGREN; ) ERIK SEIDEL; ANDREW BLOCH; MIKE ) MATUSOW; GUS HANSON; ALLEN ) CUNNINGHAM; PATRICK ANTONIUS and ) JOHN DOES 1-100 ) Defendant. ) ) __________________________________________) DEFENDANTS’ NOTICE OF MOTION TO DISMISS PLAINTIFFS’ COMPLAINT PLEASE TAKE NOTICE that Defendants, TILTWARE, LLC; VANTAGE, LTD.; FILCO, LTD.; POCKET KINGS LTD.; POCKET KINGS CONSULTING LTD.; HOWARD LEDERER; CHRISTOPHER FERGUSON; JENNIFER HARMAN-TRANIELLO, ERICK LINDGREN; ERICK SEIDEL; ANDREW BLOCH; MIKE MATUSOW; and ALLEN CUNNINGHAM, respectfully submit their Motion to Dismiss Plaintiffs’ Complaint. Specifically, Defendants move to dismiss Plaintiffs’ Complaint in its entirety pursuant to Federal Rule of Civil Procedure 12(b)(2) for lack of personal jurisdiction and Rule 12(b)(6) for failure to state a claim upon which relief can be granted under the Racketeering Influenced and Corrupt Dockets.Justia.com Organizations Act (“RICO”), 18 U.S.C. § 1961, et seq., and for failure to state a conversion claim. The grounds for Defendants’ Motion to Dismiss Plaintiffs’ Complaint are more fully set forth in the accompanying Memorandum of Law filed contemporaneously herewith. -

9Jml1,#W') T2 Vs
Case 2:11-cv-08591-MMM-AGR Document 1 Filed 10/17/11 Page 1 of 15 Page ID #:1 c, Ci; - i'a 'n € Sanai, SB#150387 1 Cyrus M. f< SANAIS -{ C:'= (r:r.;: i,' (a 2 433 North Camden Drive r !1 { -r'l "-. Suite 600 l'il:? -l 7 t:r.. t r 3 Beverly Hills, Californiq 90210 .->-{--| rfl Telephone: (irO) 7 17 -9840 - i, T lrr a't C] 4 cyrus@)sanalslaw.com ,.| oc ;.(.'5f) (., for Lary Kennedy and Greg Omotoy 5 Counsel 7tt { 6 1 8 UNITED STATES DISTRICT COURT OF TT{E CENTRAL DISTRICT OF CALIFORNIA 9 LARY KENNEDY, an individual, and GREG ) Case No.: 1_0 oMoroY'anindividuar 11 Plaintiffs, r iC"u-L1",o$"[9Jml1,#w') t2 vs. (I) MONEY HAD AND RECEIVED (2) I.INruST ENRICHMENT 13 CHRIS FERGUSON, an individual; (3) RELIEF UNDER CONSUMERS LEGAL HOWARD LEDERER, an individual; REMEDY ACT, CALIFORNIA CIVIL CODE 74 RAYMOND BITA& an individual; PHILLP SECTION I75O; GORDON, an individual; ANDY BLOCH, an (4) FRAUD 15 individual; PHIL IVEY, an individual;, (5) RELIEF UNDER CALIFORNIA PERRY FRIEDMAN, an individual; JOHN BUSINESS A}ID PROFESSIONS CODE L6 ruANDA, an individual; ERIK LINDGREN, SECTTON 17200 ET SEQ. an individual; ERIK SEIDEL, an individual; (6) RELIEF UNDER THE RACKETEER. 77 MCIIAEL MATUSOW, an individual; INFLUENCED CORRUPT ALLEN CUNNINGHAIVI, an individual; GUS oRGANIZATIONS ACT (',RICO*), 18 U.S.C. 18 HANSEN, an individual; PATRIK $ le64 ET SEQ; ANTOMUS, an individual; RAFE FURST, an (7) CONSTRUCTTVE TRUST 19 individual; TILTWARE LLC, a California limited liability company; POCKET KINGS JURY DEMAND 20 LTD, an Irish limited company; KOLYMA CORPORATION A. -

Media Guide World Series of Poker Main Event Final Table November 10-11, 2014
*JACOBSON*LARRABE*NEWHOUSE*PAPPACONSTANTINOU*POLITANO*SINDELAR*STEPHENSEN*TONKING*VAN HOOF* Media Guide World Series of Poker Main Event Final Table November 10-11, 2014 Live on ESPN2 at 5 pm PT Monday Live on ESPN at 6 pm PT Tuesday Penn & Teller Theater Rio® All-Suite Hotel & Casino *JACOBSON*LARRABE*NEWHOUSE*PAPPACONSTANTINOU*POLITANO*SINDELAR*STEPHENSEN*TONKING*VAN HOOF* 1 2014 WSOP NOVEMBER NINE Media Guide Documents: Cover Page……………………………………………………………………………………………………1 Table of Contents……………………………………………………………………………………………..2 Important Notes for Media……………………………………………………………………………………3 FINAL TABLE INFORMATION Where We Are and Where We Left Off……………………………………………………………………….4 Schedule of Events……………………………………………………………………………………………5-6 Final Table Odds Sheet………………………………………………………………………………………..7 Final Table Fact Sheet…………………………………………………………………………………………8 ESPN TV Schedule……………………………………………………………………………………………9 November Nine Chip Counts by Day…………………………………………………………………………10 Final Table Seating Chart……………………………………………………………………………………...11 Updated Payouts………………………………………………………………………………………………12 All You Need is a Chip and a Pair……………………………………………………………………………..13 MEET THE NOVEMBER NINE Seat 1: Billy Pappaconstantinou………………………………………………………………………………..14 Seat 2: Felix Stephensen……………………………………………………………………………………......15 Seat 3: Jorryt van Hoof…………………………………………………………………………………………16 Seat 4: Mark Newhouse………………………………………………………………………………………...17 Seat 5: Andoni Larrabe………………………………………………………………………………………....18 Seat 6: William Tonking………………………………………………………………………………………..19 Seat 7: Dan -

Official Media Guide
OFFICIAL MEDIA GUIDE 40th ANNUAL WORLD SERIES OF POKER May 26th- July 15, 2009 Rio Hotel, Las Vegas November Nine – November 7-10 www.worldseriesofpoker.com 1 2009 Media Guide Documents: COVER PAGE ................................................................................................................................................................................................ 1 TABLE OF CONTENTS ................................................................................................................................................................................. 2 PR CONTACT SHEET ................................................................................................................................................................................... 3 GENERAL EVENT INFORMATION: FACT SHEET .................................................................................................................................................................................................. 4 SCHEDULE..................................................................................................................................................................................................... 5 SCHEDULE..................................................................................................................................................................................................... 6 SCHEDULE.................................................................................................................................................................................................... -

Daniel Negreanu Breaks 7-Year Title Drought to Win the Inaugural Pokergo Cup Hall of Famer Says His Poker Game Is Better Than Ever
www.CardPlayer.com Vol. 34/No. 18 August 25, 2021 Daniel Negreanu Breaks 7-Year Title Drought To Win The Inaugural PokerGO Cup Hall Of Famer Says His Poker Game Is Better Than Ever SixTime Bracelet WSOP Champ Greg Tournament Strategy: Winner Layne Flack Raymer Explains How To Street By Street Passes Away Prep For The Main Event Bet Sizing PLAYER_34_17B_Cover.indd 1 8/3/21 11:13 AM PLAYER_17_GlobalPoker_DT.indd 2 7/19/21 3:58 PM PLAYER_17_GlobalPoker_DT.indd 3 7/19/21 3:58 PM Masthead - Card Player Vol. 34/No. 18 PUBLISHERS Barry Shulman | Jeff Shulman Editorial Corporate Office EDITORIAL DIRECTOR Julio Rodriguez 6940 O’Bannon Drive TOURNAMENT CONTENT MANAGER Erik Fast Las Vegas, Nevada 89117 ONLINE CONTENT MANAGER Steve Schult (702) 871-1720 Art [email protected] ART DIRECTOR Wendy McIntosh Subscriptions/Renewals 1-866-LVPOKER Website And Internet Services (1-866-587-6537) CHIEF TECHNOLOGY OFFICER Jaran Hardman PO Box 434 DATA COORDINATOR Morgan Young Congers, NY 10920-0434 Sales [email protected] ADVERTISING MANAGER Mary Hurbi Advertising Information NATIONAL SALES MANAGER Barbara Rogers [email protected] LAS VEGAS AND COLORADO SALES REPRESENTATIVE (702) 856-2206 Rich Korbin Distribution Information cardplayer Media LLC [email protected] CHAIRMAN AND CEO Barry Shulman PRESIDENT AND COO Jeff Shulman Results GENERAL COUNSEL Allyn Jaffrey Shulman [email protected] VP INTL. BUSINESS DEVELOPMENT Dominik Karelus CONTROLLER Mary Hurbi Schedules FACILITIES MANAGER Jody Ivener [email protected] Follow us www.facebook.com/cardplayer @CardPlayerMedia Card Player (ISSN 1089-2044) is published biweekly by Card Player Media LLC, 6940 O’Bannon Drive, Las Vegas, NV 89117. -
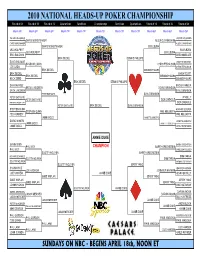
2010 Nhupc Brackets
2010 NATIONAL HEADS-UP POKER CHAMPIONSHIP Round of 64 Round of 32 Round of 16 Quarterfinals Semifinals Championship Semifinals Quarterfinals Round of 16 Round of 32 Round of 64 March 5th March 6th March 6th March 7th March 7th March 7th March 7th March 7th March 6th March 6th March 5th PATRIK ANTONIUS JESPER HOUGAARD CHRIS MONEYMAKER ALLEN CUNNINGHAM CHRIS MONEYMAKER ALLEN CUNNINGHAM CHRIS MONEYMAKER ELI ELEZRA LEO WOLPERT ELI ELEZRA LEO WOLPERT ELI ELEZRA ERIC BALDWIN GREG MUELLER ERIK SEIDEL DENNIS PHILLIPS DAVID WILLIAMS ANNETTE DWORSKI DAVID WILLIAMS CHRIS FERGUSON JOE CADA CHRIS FERGUSON ERIK SEIDEL DENNIS PHILLIPS ERIK SEIDEL KARA SCOTT ERIK SEIDEL DENNIS PHILLIPS HUCK SEED DENNIS PHILLIPS ERIK SEIDEL DENNIS PHILLIPS DAN RAMIREZ BROCK PARKER ERICK LINDGREN DOYLE BRUNSON ERICK LINDGREN DOYLE BRUNSON PETER EASTGATE DOYLE BRUNSON PETER EASTGATE JP KELLY PETER EASTGATE DON CHEADLE BERTRAND GROSPELLIER DON CHEADLE PETER EASTGATE ERIK SEIDEL DOYLE BRUNSON STEPHEN QUINN HOWARD LEDERER STEPHEN QUINN PHIL HELLMUTH TED FORREST PHIL HELLMUTH JAMIE GOLD ANNETTE OBRESTAD DARIO MINIERI ANNETTE OBRESTAD JAMIE GOLD ANNETTE OBRESTAD JAMIE GOLD OREL HERSHISER ANNIE DUKE GAVIN SMITH BARRY GREENSTEIN PHIL IVEY CHAMPION BARRY GREENSTEIN PHIL IVEY VANESSA ROUSSO SCOTTY NGUYEN BARRY GREENSTEIN RICHARD EDWARDS SAM FARHA SCOTTY NGUYEN SAM FARHA SCOTTY NGUYEN ANTONIO ESFANDIARI SCOTTY NGUYEN JERRY YANG SHAWN RICE JENNIFER HARMAN JOE HACHEM JENNIFER HARMAN JOE HACHEM ANNIE DUKE JENNIFER TILLY GABE KAPLAN JERRY YANG GABE KAPLAN JERRY YANG GABE KAPLAN JERRY YANG JOHNNY CHAN MIKE MATUSOW SCOTTY NGUYEN ANNIE DUKE DANIEL NEGREANU DARVIN MOON JASON MERCIER DARVIN MOON JASON MERCIER BILL HUNTRESS JASON MERCIER ANNIE DUKE PIETER de KORVER ANDY BLOCH PIETER de KORVER ANNIE DUKE MIKE SEXTON ANNIE DUKE JASON MERCIER ANNIE DUKE PHIL GORDON ANDREW WILSON PHIL GORDON PAUL WASICKA TOM DWAN PAUL WASICKA PHIL LAAK PAUL WASICKA PHIL LAAK GUS HANSEN PHIL LAAK GUS HANSEN JOHN JUANDA GREG RAYMER SUNDAYS ON NBC - BEGINS APRIL 18th, NOON ET. -

Can Poker Pro Freddy Deeb Win the HORSE Event at the 2008 WSO
Can poker pro Freddy Deeb win the HORSE Event at the 2008 WSOP? ... http://onlinesportshandicapping.com/news/Poker/Can-poker-pro-Freddy... Home NFL MLB NBA NHL NCAAF NCAAB Boxing MMA Soccer Other Lines search... CAPPER NEWS & DAILY PICKS POPULAR MAIN MENU NBA Playoff Picks: San Antonio Spurs at Los Angeles Cage Fury Fighting Championship: Ray Mercer vs Kimbo Home Lakers (05-23-08) Slice UFC 84 Betting Odds: B.J. Penn vs Sean Sherk Fight Kentucky Derby Betting Odds - Longshot Eight Belles Buy Sports Picks Pick and Preview (05-23-08) has chance at Kentucky Derby (04-30-08) Sports News NBA Playoffs Picks: Detroit vs Boston Game 2 Betting Illinois vs USC Rose Bowl Betting Picks Preview Predictions (05-22-08) (12-31-2007) Directory UFC 84 Betting Odds: Tito Ortiz vs. Lyoto Machida Fight "UNDEFEATED" The Hatton vs Mayweather Boxing Picks Preview (05-21-08) Picks Betting Preview! (12-03-2007) Contact Us The Chicago Bulls receive #1 pick in the NBA Draft The College Football Heisman Trophy will go to Darren Search Lottery (05-22-08) McFadden or Tim Tebow (11-25-2007) OSH Banners Home Sports News Poker Can poker pro Freddy Deeb win the HORSE Event at the 2008 WSOP? (05-22-08) About Us Can poker pro Freddy Deeb win the HORSE Event at the 2008 WSOP? (05-22-08) Terms of Service Written by Kosmo Philyako Service Map Sports Belmont Bet On Belmont Free WSOP Poker Triple Crown NBA Newsletters Betting Odds NBA Picks Qualifier Picks Playoffs WHO'S ONLINE We have 12 guests online Thursday, 22 May 2008 Username Freddy Deeb is another poker professional that came to United States to get an education and ended up becoming a Digg Password force to be reckoned with in the world of poker. -

Hidden Logic
Hidden logic In a great book, well worth reading, The“ Logic of Life”, the author, Tim Harford, has a beautiful chapter on game theory. “It is hard to say where the check-in line ends and the casino crowds begin. The bars, restaurants, and public spaces of the hotel lobby seem to ooze into the gambling floors. Even in the quiet midmorning hours, as the guests sleep off the night’s excesses or enjoy breakfast, the hotel’s lobby boasts a bewildering array of flashing lights and garish displays. Elderly gamblers in the middle-American uniform of baseball caps, slack khaki shorts, and bulging T-shirts sit and feed quarters into the maw of the nearest slot machines. Sometimes the machines form a cocooning embrace as the seniors ride them like motorized wheelchairs. Occasionally-just often enough- the machines vomit coins into the laps of their riders. Despite every effort to stimulate the senses, this is a tedious place, but the monotony is interrupted by a strange procession: A long-limbed man, his face concealed by a wall of facial hair, mirror shades, and a cowboy hat, strides across the lobby. He is pursued by admirers and stops whenever requested-which is every ten yards or so-to sign an autograph or pose with a fan for a cell phone photo. Known to poker lovers as “Jesus,” he is Chris Ferguson, one of the most recognizable and successful players in the world. He’s in Las Vegas to try to reclaim his crown as World Poker Champion. Ferguson, who is reported to have won more than five million dollars in tournament play, is the best of a new generation of players trying to conquer poker with the branch of economics known as “game theory.” It is a curious struggle, one that has pitted bespectacled geeks against hardened gamblers. -

World Series of Poker (Wsop)
OFFICIAL MEDIA GUIDE 42nd ANNUAL WORLD SERIES OF POKER May 31 - July 19, 2011 Rio All-Suite Hotel & Casino, Las Vegas November Nine – November 5-7 www.WSOP.com 1 2011 Media Guide Documents: COVER PAGE ................................................................................................................................................................................................1 TABLE OF CONTENTS............................................................................................................................................................................. 2-3 WSOP COMMUNICATIONS TEAM ............................................................................................................................................................4 2011 WSOP INFORMATION: DAILY TIME SCHEDULE ...................................................................................................................................................................... 6-10 ABOUT THE WSOP.....................................................................................................................................................................................11 FACT SHEET – 2011 WSOP........................................................................................................................................................................12 2011 ESPN TV SCHEDULE.........................................................................................................................................................................13