DOCSLIB.ORG

Evidence from Exercises of Executive Stock Options

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Evidence from Exercises of Executive Stock Options This article was downloaded by: [128.255.246.218] On: 08 September 2017, At: 11:21 Publisher: Institute for Operations Research and the Management Sciences (INFORMS) INFORMS is located in Maryland, USA Management Science Publication details, including instructions for authors and subscription information: http://pubsonline.informs.org Do Stock Options Overcome Managerial Risk Aversion? Evidence from Exercises of Executive Stock Options Randall A. Heron, Erik Lie To cite this article: Randall A. Heron, Erik Lie (2017) Do Stock Options Overcome Managerial Risk Aversion? Evidence from Exercises of Executive Stock Options. Management Science 63(9):3057-3071. https://doi.org/10.1287/mnsc.2016.2485 Full terms and conditions of use: http://pubsonline.informs.org/page/terms-and-conditions This article may be used only for the purposes of research, teaching, and/or private study. Commercial use or systematic downloading (by robots or other automatic processes) is prohibited without explicit Publisher approval, unless otherwise noted. For more information, contact [email protected]. The Publisher does not warrant or guarantee the article’s accuracy, completeness, merchantability, fitness for a particular purpose, or non-infringement. Descriptions of, or references to, products or publications, or inclusion of an advertisement in this article, neither constitutes nor implies a guarantee, endorsement, or support of claims made of that product, publication, or service. Copyright © 2016, INFORMS Please scroll down for article—it is on subsequent pages INFORMS is the largest professional society in the world for professionals in the fields of operations research, management science, and analytics. For more information on INFORMS, its publications, membership, or meetings visit http://www.informs.org MANAGEMENT SCIENCE Vol. 63, No. 9, September 2017, pp. 3057–3071 http://pubsonline.informs.org/journal/mnsc/ ISSN 0025-1909 (print), ISSN 1526-5501 (online) Do Stock Options Overcome Managerial Risk Aversion? Evidence from Exercises of Executive Stock Options Randall A. Heron,a Erik Lieb a Kelley School of Business, Indiana University, Indianapolis, Indiana 46202; b Henry B. Tippie College of Business, University of Iowa, Iowa City, Iowa 52242 Contact: [email protected] (RAH); [email protected] (EL) Received: June 24, 2014 Abstract. We report that the probability that executives exercise options early decreases Revised: May 19, 2015; December 17, 2015; with the volatility of the underlying stock return. We interpret this to mean that executives’ February 2, 2016 subjective option value increases with volatility and that option grants increase executives’ Accepted: February 15, 2016 risk appetite. Further decomposition reveals that the results are most pronounced for Published Online in Articles in Advance: idiosyncratic volatility, consistent with our conjecture that executives believe they can July 14, 2016 better predict or influence the resolution of idiosyncratic uncertainty than systematic https://doi.org/10.1287/mnsc.2016.2485 uncertainty and, thus, favor the former. Copyright: © 2016 INFORMS History: Accepted by Wei Jiang, finance. Keywords: finance • corporate finance • management • executive compensation 1. Introduction Bettis et al. (2005) explore ESO values and incentives Jensen and Meckling (1976) describe how the interests further, with a particular emphasis on the role of exer- of executives and shareholders diverge when executives cises. In their utility-based valuation model (which is maximize their own utility rather than shareholders’ an extension of Carpenter 1998), executives exercise if wealth. Without proper incentives, executives generally the stock price reaches a “threshold price,” such that prefer to consume perquisites and undertake less risk the utility from locking in the gain exceeds the util- than what optimizes firm value. Jensen and Meckling ity from holding the option. Bettis et al. (2005) esti- suggest that one solution to reduce the divergence of mate that an increase in the stock price volatility from interests is “to establish incentive compensation sys- the base-case parameterization of 39% to 58% is asso- tems for the manager or to give him stock options which ciated with a higher stock price upon exercise and in effect give him a claim on the upper tail of the out- a higher subjective valuation. Thus, it appears that come distribution” (p. 353). Other studies, including higher volatility raises the threshold price as executives Smith and Stulz (1985) and Guay (1999), support the place greater value on holding the options. They fur- ther calibrate their model to a sample of option grants view that option-based compensation mitigates man- in the Execucomp database between 1992 and 2002 and agerial risk aversion and induces greater risk-taking report that the average subjective convexity is positive. behavior. The underpinning for these studies is that Overall, the theoretical studies provide equivocal the objective option value, e.g., the Black–Scholes value, predictions on the effect of ESOs on executives’ risk is a convex function of the stock value and therefore appetite. Past empirical studies provide evidence using increases with stock price volatility. two different testing frameworks, and thus we place However, two factors complicate the application of the studies in two different camps. The first camp, objective value functions for executive stock options to which our study belongs, examines the effect of (ESOs). First, ESOs are not easily transferable; i.e., stock return volatility on the timing of ESO exercises. executives cannot sell ESOs nor fully hedge their If risk enhances executives’ subjective ESO valuation exposure without violating company policies. Second, (meaning that ESOs increase risk appetite), higher risk executives are inherently undiversified, with dispro- should discourage executives from early exercise. Con- portionate financial and human capital invested in the Downloaded from informs.org by [128.255.246.218] on 08 September 2017, at 11:21 . For personal use only, all rights reserved. sistent with this view, Carpenter et al. (2013) report company. On this backdrop, Lambert et al. (1991), that employees retain their options when volatility Carpenter (2000), Hall and Murphy (2002), and Ross is high, with the caveat that the employees in their (2004) show that risk-averse executives place a lower sample include nonexecutives, whereas Izhakian and value on their ESOs than do diversified investors and Yermack (2016) find that executives retain options in that the concavity of executives’ utility functions could the presence of high volatility. In addition, Huddart eclipse the convexity of the option payoffs, in which and Lang (1996) document evidence, albeit statistically case ESOs would encourage less risk-taking behavior. weak, that the top five percent level employees retain 3057 Heron and Lie: Do Stock Options Overcome Managerial Risk Aversion? 3058 Management Science, 2017, vol. 63, no. 9, pp. 3057–3071, © 2016 INFORMS options when volatility is high. Conversely, Hemmer the original grants. The advantage of this approach et al. (1996), Bettis et al. (2005), and Klein and Maug is that we get valuable information about the options (2011) find that executives are more likely to exercise from the original grant filings (including the total num- their options early in the presence of high volatility.1 ber of options granted, years to maturity, and vesting However, unlike the former three studies, these lat- dates) and can track what happens to the options over ter three studies compare early exercises to late exer- time. Also, our approach allows us to compare the deci- cises, which makes their results susceptible to secular sion to exercise options to contemporaneous decisions not trends. As an example, stock prices are often described to exercise options rather than to later decisions to exer- as a stochastic process with a positive drift. It follows cise options. Thus, we mitigate the concern caused by that, all else equal, later exercises will be associated systematic time-trends in the covariates. with higher moneyness than early exercises, yielding We find that high volatility discourages executives the potentially misleading inference that executives from exercising their options. We also show that the are more likely to exercise options early when they difference in results in our study versus those in earlier are less in-the-money. Another possibility is that stock studies is primarily attributable to our methodology of price volatility naturally declines as firms mature, such comparing early exercises to nonexercises rather than that early exercises are associated with higher volatil- to late exercises. We interpret our results as evidence ity. Indeed, in our sample, both total and idiosyncratic that executives place a higher value on ESOs when volatility tends to decline from the year of the option volatility is high. Thus, to the extent that the execu- grants through the maturity year. tives are inherently risk averse, the convexity of the The second empirical camp leaps the question of option payoff overcomes the concavity of their utility whether ESOs increase risk appetite to the ques- functions. tion of whether ESOs lead to greater risk taking. We further examine the differential effects of Numerous studies report that ESOs (often measured idiosyncratic volatility and systematic volatility. by their objective convexity) lead to riskier corpo- Armstrong and Vashishtha (2012) argue
Load more

Recommended publications
  • FINANCIAL DERIVATIVES SAMPLE QUESTIONS Q1. a Strangle Is an Investment Strategy That Combines A. a Call and a Put for the Same
    FINANCIAL DERIVATIVES SAMPLE QUESTIONS Q1. A strangle is an investment strategy that combines a. A call and a put for the same expiry date but at different strike prices b. Two puts and one call with the same expiry date c. Two calls and one put with the same expiry dates d. A call and a put at the same strike price and expiry date Answer: a. Q2. A trader buys 2 June expiry call options each at a strike price of Rs. 200 and Rs. 220 and sells two call options with a strike price of Rs. 210, this strategy is a a. Bull Spread b. Bear call spread c. Butterfly spread d. Calendar spread Answer c. Q3. The option price will ceteris paribus be negatively related to the volatility of the cash price of the underlying. a. The statement is true b. The statement is false c. The statement is partially true d. The statement is partially false Answer: b. Q 4. A put option with a strike price of Rs. 1176 is selling at a premium of Rs. 36. What will be the price at which it will break even for the buyer of the option a. Rs. 1870 b. Rs. 1194 c. Rs. 1140 d. Rs. 1940 Answer b. Q5 A put option should always be exercised _______ if it is deep in the money a. early b. never c. at the beginning of the trading period d. at the end of the trading period Answer a. Q6. Bermudan options can only be exercised at maturity a.
    [Show full text]
  • Up to EUR 3,500,000.00 7% Fixed Rate Bonds Due 6 April 2026 ISIN
    Up to EUR 3,500,000.00 7% Fixed Rate Bonds due 6 April 2026 ISIN IT0005440976 Terms and Conditions Executed by EPizza S.p.A. 4126-6190-7500.7 This Terms and Conditions are dated 6 April 2021. EPizza S.p.A., a company limited by shares incorporated in Italy as a società per azioni, whose registered office is at Piazza Castello n. 19, 20123 Milan, Italy, enrolled with the companies’ register of Milan-Monza-Brianza- Lodi under No. and fiscal code No. 08950850969, VAT No. 08950850969 (the “Issuer”). *** The issue of up to EUR 3,500,000.00 (three million and five hundred thousand /00) 7% (seven per cent.) fixed rate bonds due 6 April 2026 (the “Bonds”) was authorised by the Board of Directors of the Issuer, by exercising the powers conferred to it by the Articles (as defined below), through a resolution passed on 26 March 2021. The Bonds shall be issued and held subject to and with the benefit of the provisions of this Terms and Conditions. All such provisions shall be binding on the Issuer, the Bondholders (and their successors in title) and all Persons claiming through or under them and shall endure for the benefit of the Bondholders (and their successors in title). The Bondholders (and their successors in title) are deemed to have notice of all the provisions of this Terms and Conditions and the Articles. Copies of each of the Articles and this Terms and Conditions are available for inspection during normal business hours at the registered office for the time being of the Issuer being, as at the date of this Terms and Conditions, at Piazza Castello n.
    [Show full text]
  • Launch Announcement and Supplemental Listing Document for Callable Bull/Bear Contracts Over Single Equities
    6 August 2021 Hong Kong Exchanges and Clearing Limited (“HKEX”), The Stock Exchange of Hong Kong Limited (the “Stock Exchange”) and Hong Kong Securities Clearing Company Limited take no responsibility for the contents of this document, make no representation as to its accuracy or completeness and expressly disclaim any liability whatsoever for any loss howsoever arising from or in reliance upon the whole or any part of the contents of this document. This document, for which we and our Guarantor accept full responsibility, includes particulars given in compliance with the Rules Governing the Listing of Securities on the Stock Exchange of Hong Kong Limited (the “Rules”) for the purpose of giving information with regard to us and our Guarantor. We and our Guarantor, having made all reasonable enquiries, confirm that to the best of our knowledge and belief the information contained in this document is accurate and complete in all material respects and not misleading or deceptive, and there are no other matters the omission of which would make any statement herein or this document misleading. This document is for information purposes only and does not constitute an invitation or offer to acquire, purchase or subscribe for the CBBCs. The CBBCs are complex products. Investors should exercise caution in relation to them. Investors are warned that the price of the CBBCs may fall in value as rapidly as it may rise and holders may sustain a total loss of their investment. Prospective purchasers should therefore ensure that they understand the nature of the CBBCs and carefully study the risk factors set out in the Base Listing Document (as defined below) and this document and, where necessary, seek professional advice, before they invest in the CBBCs.
    [Show full text]
  • Estimation of Employee Stock Option Exercise Rates and Firm Cost⇤
    Estimation of Employee Stock Option Exercise Rates and Firm Cost⇤ Jennifer N. Carpenter Richard Stanton Nancy Wallace New York University U.C. Berkeley U.C. Berkeley December 1, 2017 Abstract We develop the first empirical model of employee-stock-option exercise that is suitable for valu- ation and allows for behavioral channels in the determination of employee option cost. We estimate exercise rates as functions of option, stock and employee characteristics in a sample of all employee exercises at 89 firms. Increasing vesting date frequency from annual to monthly reduces option value by 10-16%. Men exercise faster than women, reducing option value by 2-4%. Top employees exercise more slowly than lower-ranked, increasing value by 2-10%. Finally, we develop an analytic valuation approximation that is much more accurate than methods used in practice. ⇤Financial support from the Fisher Center for Real Estate and Urban Economics and the Society of Actuaries is gratefully acknowledged. For helpful comments and suggestions, we thank Daniel Abrams, Terry Adamson, Xavier Gabaix, Wenxuan Hou, James Lecher, Kai Li, Ulrike Malmendier, Kevin Mur- phy, Terry Odean, Nicholas Reitter, Jun Yang, David Yermack, and seminar participants at Cheung Kong Graduate School of Business, Erasmus University, Federal Reserve Bank of New York, Fudan University, Lancaster University, McGill University, New York University, The Ohio State University, Oxford Univer- sity, Peking University, Rice University, Securities and Exchange Commission, Shanghai Advanced Institute of Finance, Temple University, Tilburg University, Tsinghua University, and the 2017 Western Finance As- sociation meetings. We thank Terry Adamson at AON Consulting for providing some of the data used in this study.
    [Show full text]
  • RT Options Scanner Guide
    RT Options Scanner Introduction Our RT Options Scanner allows you to search in real-time through all publicly traded US equities and indexes options (more than 170,000 options contracts total) for trading opportunities involving strategies like: - Naked or Covered Write Protective Purchase, etc. - Any complex multi-leg option strategy – to find the “missing leg” - Calendar Spreads Search is performed against our Options Database that is updated in real-time and driven by HyperFeed’s Ticker-Plant and our Implied Volatility Calculation Engine. We offer both 20-minute delayed and real-time modes. Unlike other search engines using real-time quotes data only our system takes advantage of individual contracts Implied Volatilities calculated in real-time using our high-performance Volatility Engine. The Scanner is universal, that is, it is not confined to any special type of option strategy. Rather, it allows determining the option you need in the following terms: – Cost – Moneyness – Expiry – Liquidity – Risk The Scanner offers Basic and Advanced Search Interfaces. Basic interface can be used to find options contracts satisfying, for example, such requirements: “I need expensive Calls for Covered Call Write Strategy. They should expire soon and be slightly out of the money. Do not care much as far as liquidity, but do not like to bear high risk.” This can be done in five seconds - set the search filters to: Cost -> Dear Moneyness -> OTM Expiry -> Short term Liquidity -> Any Risk -> Moderate and press the “Search” button. It is that easy. In fact, if your request is exactly as above, you can just press the “Search” button - these values are the default filtering criteria.
    [Show full text]
  • Valuation of Stock Options
    VALUATION OF STOCK OPTIONS The right to buy or sell a given security at a specified time in the future is an option. Options are “derivatives’, i.e. they derive their value from the security that is to be traded in accordance with the option. Determining the value of publicly traded stock options is not a problem as the market sets the price. The value of a non-publicly traded option, however, depends on a number of factors: the price of the underlying security at the time of valuation, the time to exercise the option, the volatility of the underlying security, the risk free interest rate, the dividend rate, and the strike price. In addition to these financial variables, subjective variables also play a role. For example, in the case of employee stock options, the employee and the employer have different reasons for valuation, and, therefore, differing needs result in a different valuation for each party. This appendix discusses the reasons for the valuation of non-publicly traded options, explores and compares the two predominant valuation models, and attempts to identify the appropriate valuation methods for a variety of situations. We do not attempt to explain option-pricing theory in depth nor do we attempt mathematical proofs of the models. We focus on the practical aspects of option valuation, directing the reader to the location of computer calculators and sources of the data needed to enter into those calculators. Why Value? The need for valuation arises in a variety of circumstances. In the valuation of a business, for example, options owned by that business must be valued like any other investment asset.
    [Show full text]
  • 11 Option Payoffs and Option Strategies
    11 Option Payoffs and Option Strategies Answers to Questions and Problems 1. Consider a call option with an exercise price of $80 and a cost of $5. Graph the profits and losses at expira- tion for various stock prices. 73 74 CHAPTER 11 OPTION PAYOFFS AND OPTION STRATEGIES 2. Consider a put option with an exercise price of $80 and a cost of $4. Graph the profits and losses at expiration for various stock prices. ANSWERS TO QUESTIONS AND PROBLEMS 75 3. For the call and put in questions 1 and 2, graph the profits and losses at expiration for a straddle comprising these two options. If the stock price is $80 at expiration, what will be the profit or loss? At what stock price (or prices) will the straddle have a zero profit? With a stock price at $80 at expiration, neither the call nor the put can be exercised. Both expire worthless, giving a total loss of $9. The straddle breaks even (has a zero profit) if the stock price is either $71 or $89. 4. A call option has an exercise price of $70 and is at expiration. The option costs $4, and the underlying stock trades for $75. Assuming a perfect market, how would you respond if the call is an American option? State exactly how you might transact. How does your answer differ if the option is European? With these prices, an arbitrage opportunity exists because the call price does not equal the maximum of zero or the stock price minus the exercise price. To exploit this mispricing, a trader should buy the call and exercise it for a total out-of-pocket cost of $74.
    [Show full text]
  • The Promise and Peril of Real Options
    1 The Promise and Peril of Real Options Aswath Damodaran Stern School of Business 44 West Fourth Street New York, NY 10012 [email protected] 2 Abstract In recent years, practitioners and academics have made the argument that traditional discounted cash flow models do a poor job of capturing the value of the options embedded in many corporate actions. They have noted that these options need to be not only considered explicitly and valued, but also that the value of these options can be substantial. In fact, many investments and acquisitions that would not be justifiable otherwise will be value enhancing, if the options embedded in them are considered. In this paper, we examine the merits of this argument. While it is certainly true that there are options embedded in many actions, we consider the conditions that have to be met for these options to have value. We also develop a series of applied examples, where we attempt to value these options and consider the effect on investment, financing and valuation decisions. 3 In finance, the discounted cash flow model operates as the basic framework for most analysis. In investment analysis, for instance, the conventional view is that the net present value of a project is the measure of the value that it will add to the firm taking it. Thus, investing in a positive (negative) net present value project will increase (decrease) value. In capital structure decisions, a financing mix that minimizes the cost of capital, without impairing operating cash flows, increases firm value and is therefore viewed as the optimal mix.
    [Show full text]
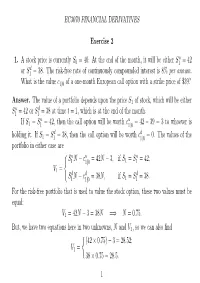
  • EC3070 FINANCIAL DERIVATIVES Exercise 2 1. a Stock Price Is Currently S0 = 40. at the End of the Month, It Will Be Either S = 42
    EC3070 FINANCIAL DERIVATIVES Exercise 2 u 1. A stock price is currently S0 = 40. At the end of the month, it will be either S1 =42 d or S1 = 38. The risk-free rate of continuously compounded interest is 8% per annum. What is the value c1|0 of a one-month European call option with a strike price of $39? Answer. The value of a portfolio depends upon the price S1 of stock, which will be either u d S1 =42orS1 = 38 at time t = 1, which is at the end of the month. u u − If S1 = S1 = 42, then the call option will be worth c1|0 =42 39 = 3 to whoever is d d holding it. If S1 = S1 = 38, then the call option will be worth c1|0 = 0. The values of the portfolio in either case are u − u − u S1 N c1|0 =42N 3, if S1 = S1 = 42; V = 1 d − d d S1 N c1|0 =38N, if S1 = S1 = 38. For the risk-free portfolio that is used to value the stock option, these two values must be equal: V1 =42N − 3=38N =⇒ N =0.75. But, we have two equations here in two unknowns, N and V , so we can also find 1 (42 × 0.75) − 3=28.52; V1 = 38 × 0.75 = 28.5. 1 EC3070 Exercise 2 When this is discounted to its present value, it must be equal to the value of the portfolio at time t =0: −r/12 V0 = S0N − c1|0 = V1e . Therefore, using exp{−8/(12 × 100)} =0.993356, we get −r/12 c | = S N − V e 1 0 0 1 = (40 × 0.75) − 28.5 × e−8/{12×100} =1.69 For an alternative solution, recall that the probability that the stock price will increase is erτ − D S (erτ − D) S erτ − Sd p = = 0 = 0 1 U − D S (U − D) Su − Sd 0 1 1 40 × e8/{12×100} − 38 = =0.5669, 42 − 38 where we have used exp{8/(12 × 100)} =1.00669.
    [Show full text]
  • Stock Options and Credit Default Swaps in Risk Management
    Stock Options and Credit Default Swaps in Risk Management Bassam Al-Own Faculty of Finance and Business Administration Al al-Bayt University Mafraq 25113, Jordan Email: [email protected] Marizah Minhat* The Business School Edinburgh Napier University Edinburgh EH14 1DJ, United Kingdom Email: [email protected] Simon Gao The Business School Edinburgh Napier University Edinburgh EH14 1DJ, United Kingdom Email: [email protected] Journal of International Financial Markets, Institutions and Money (forthcoming) * Corresponding author. Acknowledgement: This paper was presented at the 2016 Cross Country Perspectives of Finance conferences held in Taiyuan and Pu’er, China. The authors would like to thank Professor Gady Jacoby, Professor Zhenyu Wu, anonymous reviewers, and the conferences’ participants. i Stock Options and Credit Default Swaps in Risk Management 1 ABSTRACT The use of stock options and credit default swaps (CDS) in banks is not uncommon. Stock options can induce risk-taking incentives, while CDS can be used to hedge against credit risk. Building on the existing literature on executive compensation and risk management, our study contributes novel empirical support for the role of stock options in restraining the use of CDS for hedging purposes. Based on data of CEO stock options and CDS held by 60 European banks during the period 2006-2011, we find a negative relationship between option-induced risk- taking incentives (vega) and the proportion of CDS held for hedging. However, the extent of CDS held for hedging is found to be positively related to default risk in the period leading to the financial crisis that erupted in 2007.
    [Show full text]
  • LECTURE 15: AMERICAN OPTIONS 1. Introduction All of the Options That
    LECTURE 15: AMERICAN OPTIONS 1. Introduction All of the options that we have considered thus far have been of the European variety: exercise is permitted only at the termination of the contract. These are, by and large, relatively simple to price and hedge, at least under the hypotheses of the Black-Sholes model, as pricing entails only the evaluation of a single expectation. American options, which may be exercised at any time up to expiration, are considerably more complicated, because to price or hedge these options one must account for many (infinitely many!) different possible exercise policies. For certain options with convex payoff functions, such as call options on stocks that pay no dividends, the optimal policy is to exercise only at expiration. In most other cases, including put options, there is also an optimal exercise policy; however, this optimal policy is rarely simple or easily computable. We shall consider the pricing and optimal exercise of American options in the simplest nontrivial setting, the Black-Sholes model, where the underlying asset Stock pays no dividends and has a price process St that behaves, under the risk-neutral measure Q, as a simple geometric Brownian motion: 2 (1) St = S0 exp σWt + (r − σ =2)t Here r ≥ 0, the riskless rate of return, is constant, and Wt is a standard Wiener process under Q. For any American option on the underlying asset Stock, the admissible exercise policies must be stopping times with respect to the natural filtration (Ft)0≤t≤T of the Wiener process Wt. If F (s) is the payoff of an American option exercised when the stock price is s, and if T is the expiration date of the option, then its value Vt at time t ≤ T is −r(τ−t) (2) Vt = sup E(F (Sτ )e j Ft): τ:t≤τ≤T 2.
    [Show full text]
  • Derivative Securities
    2. DERIVATIVE SECURITIES Objectives: After reading this chapter, you will 1. Understand the reason for trading options. 2. Know the basic terminology of options. 2.1 Derivative Securities A derivative security is a financial instrument whose value depends upon the value of another asset. The main types of derivatives are futures, forwards, options, and swaps. An example of a derivative security is a convertible bond. Such a bond, at the discretion of the bondholder, may be converted into a fixed number of shares of the stock of the issuing corporation. The value of a convertible bond depends upon the value of the underlying stock, and thus, it is a derivative security. An investor would like to buy such a bond because he can make money if the stock market rises. The stock price, and hence the bond value, will rise. If the stock market falls, he can still make money by earning interest on the convertible bond. Another derivative security is a forward contract. Suppose you have decided to buy an ounce of gold for investment purposes. The price of gold for immediate delivery is, say, $345 an ounce. You would like to hold this gold for a year and then sell it at the prevailing rates. One possibility is to pay $345 to a seller and get immediate physical possession of the gold, hold it for a year, and then sell it. If the price of gold a year from now is $370 an ounce, you have clearly made a profit of $25. That is not the only way to invest in gold.
    [Show full text]