DOCSLIB.ORG

LU Factorization LU Decomposition LU Decomposition: Motivation LU Decomposition

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
LU Factorization LU Decomposition LU Decomposition: Motivation LU Decomposition LU Factorization LU Decomposition To further improve the efficiency of solving linear systems Factorizations of matrix A : LU and QR A matrix A can be decomposed into a lower triangular matrix L and upper triangular matrix U so that LU Factorization Methods: Using basic Gaussian Elimination (GE) A = LU ◦ Factorization of Tridiagonal Matrix ◦ LU decomposition is performed once; can be used to solve multiple Using Gaussian Elimination with pivoting ◦ right hand sides. Direct LU Factorization ◦ Similar to Gaussian elimination, care must be taken to avoid roundoff Factorizing Symmetrix Matrices (Cholesky Decomposition) ◦ errors (partial or full pivoting) Applications Special Cases: Banded matrices, Symmetric matrices. Analysis ITCS 4133/5133: Intro. to Numerical Methods 1 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 2 LU/QR Factorization LU Decomposition: Motivation LU Decomposition Forward pass of Gaussian elimination results in the upper triangular ma- trix 1 u12 u13 u1n 0 1 u ··· u 23 ··· 2n U = 0 0 1 u3n . ···. 0 0 0 1 ··· We can determine a matrix L such that LU = A , and l11 0 0 0 l l 0 ··· 0 21 22 ··· L = l31 l32 l33 0 . ···. . l l l 1 n1 n2 n3 ··· ITCS 4133/5133: Intro. to Numerical Methods 3 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 4 LU/QR Factorization LU Decomposition via Basic Gaussian Elimination LU Decomposition via Basic Gaussian Elimination: Algorithm ITCS 4133/5133: Intro. to Numerical Methods 5 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 6 LU/QR Factorization LU Decomposition of Tridiagonal Matrix Banded Matrices Matrices that have non-zero elements close to the main diagonal Example: matrix with a bandwidth of 3 (or half band of 1) a11 a12 0 0 0 a21 a22 a23 0 0 0 a32 a33 a34 0 0 0 a43 a44 a45 0 0 0 a a 54 55 Efficiency: Reduced pivoting needed, as elements below bands are zero. Iterative techniques are generally more efficient for sparse matrices, such as banded systems. ITCS 4133/5133: Intro. to Numerical Methods 7 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 8 LU/QR Factorization LU Decomposition via GE with Pivoting LU Decomposition of Tridiagonal Matrix: Algorithm ITCS 4133/5133: Intro. to Numerical Methods 9 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 10 LU/QR Factorization LU Decomposition via GE with Pivoting: Algorithm Direct LU Decomposition l11 0 0 0 1 u12 u13 u1n a11 a12 a13 a1n l l 0 ··· 0 0 1 u ··· u a a a ··· a 21 22 ··· 23 ··· 2n 21 22 23 ··· 2n l31 l32 l33 0 0 0 1 u3n = a31 a32 a33 a2n . ···. ···. . ···. . . ln1 ln2 ln3 1 0 0 0 1 an1 an2 an3 ann ··· ··· ··· The above equation shows the coefficient matrix A can be decomposed into L and U; L and U can be determined by the computing the product and equating like terms. ITCS 4133/5133: Intro. to Numerical Methods 11 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 12 LU/QR Factorization Direct LU Decomposition: Example Determining L and U li1 = ai1, i = 1, 2, . , n a1j u1j = , j = 2, 3, . , n l11 j 1 − l = a l u , ij ij − ik kj k=1 for j X= 2, 3, . , n 1 and i = j, j + 1, . , n j 1 − a − l u u = ji − k=1 jk ki , ji l Pjj for j = 2, 3, . , n 1 and i = j + 1, j + 2, . , n n 1 − − l = a l u nn nn − nk kn k=1 X ITCS 4133/5133: Intro. to Numerical Methods 13 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 14 LU/QR Factorization Direct LU Decomposition: Algorithm Symmetric Matrices Symmetric square matrices - common in engineering, for example stiffness matrix (stiffness properties of structures). For a symmetric matrix A A = AT where AT is the transpose of A. Hence For a symmetric matrix A A = LLT ITCS 4133/5133: Intro. to Numerical Methods 15 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 16 LU/QR Factorization LU (Cholesky) Decomposition of Symmetric Matrices Symmetric Matrices: LU Decomposition We can use Cholesky Decomposition to compute the LU decompo- sition of A l11 = √a11 i 1 − l = a l2 , for i = 2, 3, . , n ii v ii − ik u k=1 u Xj 1 taij − likljk l = − k=1 , for j = 2, 3, . , i 1, and j < 1 ij l − Pjj ITCS 4133/5133: Intro. to Numerical Methods 17 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 18 LU/QR Factorization LU (Cholesky) Decomposition: Algorithm Applications of LU Decomposition:Solving Linear systems [A]X~ = [L][U][X~ ] = C = [L]~e = C where ~e = [U]X~ Solve for ~e using L (forward substitution) Solve for X~ using U (back substitution) ITCS 4133/5133: Intro. to Numerical Methods 19 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 20 LU/QR Factorization Solving Linear Systems: Example Solving Linear Systems Forward Substitution Solve for ~e, C1 e1 = l11 n Ci j=1 lijej ei = − , for i = 2, 3, . n Plii Back Substitution Solve for X~ Xn = en n X = e u X , for i = n 1, n 2,... 1 i i − ij j − − j=i+1 X ITCS 4133/5133: Intro. to Numerical Methods 21 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 22 LU/QR Factorization Solving Linear Systems: Algorithm Application 2: Tridiagonal Systems ITCS 4133/5133: Intro. to Numerical Methods 23 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 24 LU/QR Factorization Application 3: Matrix Inverse Analysis: LU Decomposition Why does LU decomposition work? Consider the first elimination step: 1 0 0 a11 a12 a13 a11 a12 a13 0 0 m21 1 0 a21 a22 a23 = 0 a22 a23 0 0 m31 0 1 a31 a32 a33 0 a32 a33 Define 1 0 0 1 0 0 M = m 1 0 ,M = 0 1 0 1 21 2 m31 0 1 0 m32 1 Hence 1 0 0 1 0 0 1 1 M1− = m21 1 0 ,M2− = 0 1 0 , −m 0 1 0 m 1 − 31 − 32 ITCS 4133/5133: Intro. to Numerical Methods 25 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 26 LU/QR Factorization Analysis:LU Decomposition with Pivoting Decomposition results in the factorization of PA, where P is the Analysis: LU Decomposition permutation matrix. 1 0 0 a11 a12 a13 a11 a12 a13 0 1 0 a21 a22 a23 = a21 a22 a23 Gradual tranformation of I towards LU: 0 0 1 a31 a32 a33 a31 a32 a33 I.A = A Assume no pivoting in column 1, pivoting in column 2: 1 I.M1− .M1.A = A 1 1 I.A = A I.M1− .M2− .M2.M1.A = A 1 I.M1− .M1.A = A 1 1 1 M2.M1.A is U and I.M1− .M2− is L, given by I.M1− .P.P.M1.A = A 1 1 I.M1− .P.M2− .M2.P.M1.A = A 1 0 0 m 1 0 1 1 21 M2.P.M1.A is upper triangular, but I.M1− .P.M2− is not lower tri- −m m 1 − 31 − 32 angular. Premultiply both sides by P : 1 1 PM1− .P.M2− .M2.P.M1.A = P.A ITCS 4133/5133: Intro. to Numerical Methods 27 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 28 LU/QR Factorization ITCS 4133/5133: Intro. to Numerical Methods 29 LU/QR Factorization.
Load more

Recommended publications
  • Recursive Approach in Sparse Matrix LU Factorization
    51 Recursive approach in sparse matrix LU factorization Jack Dongarra, Victor Eijkhout and the resulting matrix is often guaranteed to be positive Piotr Łuszczek∗ definite or close to it. However, when the linear sys- University of Tennessee, Department of Computer tem matrix is strongly unsymmetric or indefinite, as Science, Knoxville, TN 37996-3450, USA is the case with matrices originating from systems of Tel.: +865 974 8295; Fax: +865 974 8296 ordinary differential equations or the indefinite matri- ces arising from shift-invert techniques in eigenvalue methods, one has to revert to direct methods which are This paper describes a recursive method for the LU factoriza- the focus of this paper. tion of sparse matrices. The recursive formulation of com- In direct methods, Gaussian elimination with partial mon linear algebra codes has been proven very successful in pivoting is performed to find a solution of Eq. (1). Most dense matrix computations. An extension of the recursive commonly, the factored form of A is given by means technique for sparse matrices is presented. Performance re- L U P Q sults given here show that the recursive approach may per- of matrices , , and such that: form comparable to leading software packages for sparse ma- LU = PAQ, (2) trix factorization in terms of execution time, memory usage, and error estimates of the solution. where: – L is a lower triangular matrix with unitary diago- nal, 1. Introduction – U is an upper triangular matrix with arbitrary di- agonal, Typically, a system of linear equations has the form: – P and Q are row and column permutation matri- Ax = b, (1) ces, respectively (each row and column of these matrices contains single a non-zero entry which is A n n A ∈ n×n x where is by real matrix ( R ), and 1, and the following holds: PPT = QQT = I, b n b, x ∈ n and are -dimensional real vectors ( R ).
    [Show full text]
  • Lecture 5 - Triangular Factorizations & Operation Counts
    Lecture 5 - Triangular Factorizations & Operation Counts LU Factorization We have seen that the process of GE essentially factors a matrix A into LU. Now we want to see how this factorization allows us to solve linear systems and why in many cases it is the preferred algorithm compared with GE. Remember on paper, these methods are the same but computationally they can be different. First, suppose we want to solve A~x = ~b and we are given the factorization A = LU. It turns out that the system LU~x = ~b is \easy" to solve because we do a forward solve L~y = ~b and then back solve U~x = ~y. We have seen that we can easily implement the equations for the back solve and for homework you will write out the equations for the forward solve. Example If 0 2 −1 2 1 0 1 0 0 1 0 2 −1 2 1 A = @ 4 1 9 A = LU = @ 2 1 0 A @ 0 3 5 A 8 5 24 4 3 1 0 0 1 solve the linear system A~x = ~b where ~b = (0; −5; −16)T . ~ We first solve L~y = b to get y1 = 0, 2y1 +y2 = −5 implies y2 = −5 and 4y1 +3y2 +y3 = −16 T implies y3 = −1. Now we solve U~x = ~y = (0; −5; −1) . Back solving yields x3 = −1, 3x2 + 5x3 = −5 implies x2 = 0 and finally 2x1 − x2 + 2x3 = 0 implies x1 = 1 giving the solution (1; 0; −1)T . If GE and LU factorization are equivalent on paper, why would one be computationally advantageous in some settings? Recall that when we solve A~x = ~b by GE we must also multiply the right hand side by the Gauss transformation matrices.
    [Show full text]
  • LU-Factorization 1 Introduction 2 Upper and Lower Triangular Matrices
    MAT067 University of California, Davis Winter 2007 LU-Factorization Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 12, 2007) 1 Introduction Given a system of linear equations, a complete reduction of the coefficient matrix to Reduced Row Echelon (RRE) form is far from the most efficient algorithm if one is only interested in finding a solution to the system. However, the Elementary Row Operations (EROs) that constitute such a reduction are themselves at the heart of many frequently used numerical (i.e., computer-calculated) applications of Linear Algebra. In the Sections that follow, we will see how EROs can be used to produce a so-called LU-factorization of a matrix into a product of two significantly simpler matrices. Unlike Diagonalization and the Polar Decomposition for Matrices that we’ve already encountered in this course, these LU Decompositions can be computed reasonably quickly for many matrices. LU-factorizations are also an important tool for solving linear systems of equations. You should note that the factorization of complicated objects into simpler components is an extremely common problem solving technique in mathematics. E.g., we will often factor a polynomial into several polynomials of lower degree, and one can similarly use the prime factorization for an integer in order to simply certain numerical computations. 2 Upper and Lower Triangular Matrices We begin by recalling the terminology for several special forms of matrices. n×n A square matrix A =(aij) ∈ F is called upper triangular if aij = 0 for each pair of integers i, j ∈{1,...,n} such that i>j. In other words, A has the form a11 a12 a13 ··· a1n 0 a22 a23 ··· a2n A = 00a33 ··· a3n .
    [Show full text]
  • LU, QR and Cholesky Factorizations Using Vector Capabilities of Gpus LAPACK Working Note 202 Vasily Volkov James W
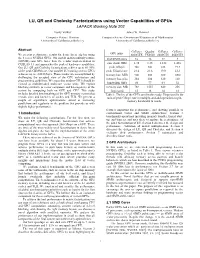
    LU, QR and Cholesky Factorizations using Vector Capabilities of GPUs LAPACK Working Note 202 Vasily Volkov James W. Demmel Computer Science Division Computer Science Division and Department of Mathematics University of California at Berkeley University of California at Berkeley Abstract GeForce Quadro GeForce GeForce GPU name We present performance results for dense linear algebra using 8800GTX FX5600 8800GTS 8600GTS the 8-series NVIDIA GPUs. Our matrix-matrix multiply routine # of SIMD cores 16 16 12 4 (GEMM) runs 60% faster than the vendor implementation in CUBLAS 1.1 and approaches the peak of hardware capabilities. core clock, GHz 1.35 1.35 1.188 1.458 Our LU, QR and Cholesky factorizations achieve up to 80–90% peak Gflop/s 346 346 228 93.3 of the peak GEMM rate. Our parallel LU running on two GPUs peak Gflop/s/core 21.6 21.6 19.0 23.3 achieves up to ~300 Gflop/s. These results are accomplished by memory bus, MHz 900 800 800 1000 challenging the accepted view of the GPU architecture and memory bus, pins 384 384 320 128 programming guidelines. We argue that modern GPUs should be viewed as multithreaded multicore vector units. We exploit bandwidth, GB/s 86 77 64 32 blocking similarly to vector computers and heterogeneity of the memory size, MB 768 1535 640 256 system by computing both on GPU and CPU. This study flops:word 16 18 14 12 includes detailed benchmarking of the GPU memory system that Table 1: The list of the GPUs used in this study. Flops:word is the reveals sizes and latencies of caches and TLB.
    [Show full text]
  • LU and Cholesky Decompositions. J. Demmel, Chapter 2.7
    LU and Cholesky decompositions. J. Demmel, Chapter 2.7 1/14 Gaussian Elimination The Algorithm — Overview Solving Ax = b using Gaussian elimination. 1 Factorize A into A = PLU Permutation Unit lower triangular Non-singular upper triangular 2/14 Gaussian Elimination The Algorithm — Overview Solving Ax = b using Gaussian elimination. 1 Factorize A into A = PLU Permutation Unit lower triangular Non-singular upper triangular 2 Solve PLUx = b (for LUx) : − LUx = P 1b 3/14 Gaussian Elimination The Algorithm — Overview Solving Ax = b using Gaussian elimination. 1 Factorize A into A = PLU Permutation Unit lower triangular Non-singular upper triangular 2 Solve PLUx = b (for LUx) : − LUx = P 1b − 3 Solve LUx = P 1b (for Ux) by forward substitution: − − Ux = L 1(P 1b). 4/14 Gaussian Elimination The Algorithm — Overview Solving Ax = b using Gaussian elimination. 1 Factorize A into A = PLU Permutation Unit lower triangular Non-singular upper triangular 2 Solve PLUx = b (for LUx) : − LUx = P 1b − 3 Solve LUx = P 1b (for Ux) by forward substitution: − − Ux = L 1(P 1b). − − 4 Solve Ux = L 1(P 1b) by backward substitution: − − − x = U 1(L 1P 1b). 5/14 Example of LU factorization We factorize the following 2-by-2 matrix: 4 3 l 0 u u = 11 11 12 . (1) 6 3 l21 l22 0 u22 One way to find the LU decomposition of this simple matrix would be to simply solve the linear equations by inspection. Expanding the matrix multiplication gives l11 · u11 + 0 · 0 = 4, l11 · u12 + 0 · u22 = 3, (2) l21 · u11 + l22 · 0 = 6, l21 · u12 + l22 · u22 = 3.
    [Show full text]
  • Math 2270 - Lecture 27 : Calculating Determinants
    Math 2270 - Lecture 27 : Calculating Determinants Dylan Zwick Fall 2012 This lecture covers section 5.2 from the textbook. In the last lecture we stated and discovered a number of properties about determinants. However, we didn’t talk much about how to calculate them. In fact, the only general formula was the nasty formula mentioned at the beginning, namely n det(A)= sgn(σ) a . X Y iσ(i) σ∈Sn i=1 We also learned a formula for calculating the determinant in a very special case. Namely, if we have a triangular matrix, the determinant is just the product of the diagonals. Today, we’re going to discuss how that special triangular case can be used to calculate determinants in a very efficient manner, and we’ll derive the nasty formula. We’ll also go over one other way of calculating a deter- minnat, the “cofactor expansion”, that, to be honest, is not all that useful computationally, but can be very useful when you need to prove things. The assigned problems for this section are: Section 5.2 - 1, 3, 11, 15, 16 1 1 Calculating the Determinant from the Pivots In practice, the easiest way to calculate the determinant of a general matrix is to use elimination to get an upper-triangular matrix with the same de- terminant, and then just calculate the determinant of the upper-triangular matrix by taking the product of the diagonal terms, a.k.a. the pivots. If there are no row exchanges required for the LU decomposition of A, then A = LU, and det(A)= det(L)det(U).
    [Show full text]
  • LU Decomposition S = LU, Then We Can  1 0 0   2 4 −2   2 4 −2  Use It to Solve Sx = F
    LU-Decomposition Example 1 Compare with Example 1 in gaussian elimination.pdf. Consider I The Gaussian elimination for the solution of the linear system Sx = f transforms the augmented matrix (Sjf) into (Ujc), where U 0 2 4 −21 is upper triangular. The transformations are determined by the S = 4 9 −3 : (1) matrix S only. @ A If we have to solve a system Sx = f~ with a different right hand side −2 −3 7 f~, then we start over. Most of the computations that lead us from We express Gaussian Elimination using Matrix-Matrix-multiplications (Sjf~) into (Ujc~), depend only on S and are identical to the steps that we executed when we applied Gaussian elimination to Sx = f. 0 1 0 0 1 0 2 4 −2 1 0 2 4 −2 1 We now express Gaussian elimination as a sequence of matrix-matrix I @ −2 1 0 A @ 4 9 −3 A = @ 0 1 1 A multiplications. This representation leads to the decomposition of S 1 0 1 −2 −3 7 0 1 5 into a product of a lower triangular matrix L and an upper triangular | {z } | {z } | {z } matrix U, S = LU. This is known as the LU-Decomposition of S. =E1 =S =E1S I If we have computed the LU decomposition S = LU, then we can 0 1 0 0 1 0 2 4 −2 1 0 2 4 −2 1 use it to solve Sx = f. @ 0 1 0 A @ 0 1 1 A = @ 0 1 1 A I We replace S by LU, 0 −1 1 0 1 5 0 0 4 LUx = f; | {z } | {z } | {z } and introduce y = Ux.
    [Show full text]
  • Scalable Sparse Symbolic LU Factorization on Gpus
    JOURNAL OF LATEX CLASS FILES, VOL. 14, NO. 8, AUGUST 2015 1 GSOFA: Scalable Sparse Symbolic LU Factorization on GPUs Anil Gaihre, Xiaoye Sherry Li and Hang Liu Abstract—Decomposing a matrix A into a lower matrix L and an upper matrix U, which is also known as LU decomposition, is an essential operation in numerical linear algebra. For a sparse matrix, LU decomposition often introduces more nonzero entries in the L and U factors than in the original matrix. A symbolic factorization step is needed to identify the nonzero structures of L and U matrices. Attracted by the enormous potentials of the Graphics Processing Units (GPUs), an array of efforts have surged to deploy various LU factorization steps except for the symbolic factorization, to the best of our knowledge, on GPUs. This paper introduces GSOFA, the first GPU-based symbolic factorization design with the following three optimizations to enable scalable LU symbolic factorization for nonsymmetric pattern sparse matrices on GPUs. First, we introduce a novel fine-grained parallel symbolic factorization algorithm that is well suited for the Single Instruction Multiple Thread (SIMT) architecture of GPUs. Second, we tailor supernode detection into a SIMT friendly process and strive to balance the workload, minimize the communication and saturate the GPU computing resources during supernode detection. Third, we introduce a three-pronged optimization to reduce the excessive space consumption problem faced by multi-source concurrent symbolic factorization. Taken together, GSOFA achieves up to 31× speedup from 1 to 44 Summit nodes (6 to 264 GPUs) and outperforms the state-of-the-art CPU project, on average, by 5×.
    [Show full text]
  • LU, QR and Cholesky Factorizations Using Vector Capabilities of Gpus LAPACK Working Note 202 Vasily Volkov James W
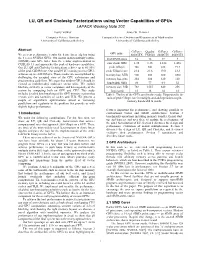
    LU, QR and Cholesky Factorizations using Vector Capabilities of GPUs LAPACK Working Note 202 Vasily Volkov James W. Demmel Computer Science Division Computer Science Division and Department of Mathematics University of California at Berkeley University of California at Berkeley Abstract GeForce Quadro GeForce GeForce GPU name We present performance results for dense linear algebra using 8800GTX FX5600 8800GTS 8600GTS the 8-series NVIDIA GPUs. Our matrix-matrix multiply routine # of SIMD cores 16 16 12 4 (GEMM) runs 60% faster than the vendor implementation in CUBLAS 1.1 and approaches the peak of hardware capabilities. core clock, GHz 1.35 1.35 1.188 1.458 Our LU, QR and Cholesky factorizations achieve up to 80–90% peak Gflop/s 346 346 228 93.3 of the peak GEMM rate. Our parallel LU running on two GPUs peak Gflop/s/core 21.6 21.6 19.0 23.3 achieves up to ~300 Gflop/s. These results are accomplished by memory bus, MHz 900 800 800 1000 challenging the accepted view of the GPU architecture and memory bus, pins 384 384 320 128 programming guidelines. We argue that modern GPUs should be viewed as multithreaded multicore vector units. We exploit bandwidth, GB/s 86 77 64 32 blocking similarly to vector computers and heterogeneity of the memory size, MB 768 1535 640 256 system by computing both on GPU and CPU. This study flops:word 16 18 14 12 includes detailed benchmarking of the GPU memory system that Table 1: The list of the GPUs used in this study. Flops:word is the reveals sizes and latencies of caches and TLB.
    [Show full text]
  • Gaussian Elimination and Lu Decomposition (Supplement for Ma511)
    GAUSSIAN ELIMINATION AND LU DECOMPOSITION (SUPPLEMENT FOR MA511) D. ARAPURA Gaussian elimination is the go to method for all basic linear classes including this one. We go summarize the main ideas. 1. Matrix multiplication The rule for multiplying matrices is, at first glance, a little complicated. If A is m × n and B is n × p then C = AB is defined and of size m × p with entries n X cij = aikbkj k=1 The main reason for defining it this way will be explained when we talk about linear transformations later on. THEOREM 1.1. (1) Matrix multiplication is associative, i.e. A(BC) = (AB)C. (Henceforth, we will drop parentheses.) (2) If A is m × n and Im×m and In×n denote the identity matrices of the indicated sizes, AIn×n = Im×mA = A. (We usually just write I and the size is understood from context.) On the other hand, matrix multiplication is almost never commutative; in other words generally AB 6= BA when both are defined. So we have to be careful not to inadvertently use it in a calculation. Given an n × n matrix A, the inverse, if it exists, is another n × n matrix A−1 such that AA−I = I;A−1A = I A matrix is called invertible or nonsingular if A−1 exists. In practice, it is only necessary to check one of these. THEOREM 1.2. If B is n × n and AB = I or BA = I, then A invertible and B = A−1. Proof. The proof of invertibility of A will need to wait until we talk about deter- minants.
    [Show full text]
  • Effective GPU Strategies for LU Decomposition H
    Effective GPU Strategies for LU Decomposition H. M. D. M. Bandara* & D. N. Ranasinghe University of Colombo School of Computing, Sri Lanka [email protected], [email protected] Abstract— GPUs are becoming an attractive computing approaches, Section 5 shows the results and platform not only for traditional graphics computation performance studies obtained on our test environment but also for general-purpose computation because of the and then finally Section 6 concludes the paper. computational power, programmability and comparatively low cost of modern GPUs. This has lead to II. RELATED WORK a variety of complex GPGPU applications with significant performance improvements. The LU A few research works on LU decomposition with decomposition represents a fundamental step in many the support of highly parallel GPU environments have computationally intensive scientific applications and it is been carried out and had not been able to accelerate it often the costly step in the solution process because of the much. In [4] Ino et al. they have developed and impact of size of the matrix. In this paper we implement evaluated some implementation methods for LU three different variants of the LU decomposition algorithm on a Tesla C1060 and the most significant LU Decomposition in terms of (a) loop processing (b) decomposition that fits the highly parallel architecture of branch processing and (c) vector processing. In [5] modern GPUs is found to be Update through Column Gappalo et al. have reduced matrix decomposition and with shared memory access implementation. row operations to a series of rasterization problems on GPU. They have mapped the problem to GPU Keywords—LU decomposition, CUDA, GPGPU architecture based on the fact that fundamental I.
    [Show full text]
  • Triangular Factorization and Inversion by Fast Matrix Multiplication*
    mathematics of computation, volume 28, number 125, January, 1974 Triangular Factorization and Inversion by Fast Matrix Multiplication* By James R. Bunch and John E. Hopcroft Abstract. The fast matrix multiplication algorithm by Strassen is used to obtain the triangular factorization of a permutation of any nonsingular matrix of ordern in <Cxnlos'7 operations, and, hence, the inverse of any nonsingular matrix in <Cürtlog'7 operations. 1. Introduction. Strassen [3] has given an algorithm using noncommutative multiplication which computes the product of two matrices of order 2 by 7 multi- plications and 18 additions. Then the product of two matrices of order mlk could be computed by m3lk multiplications and (5 + m)m2lk — 6(m2k)2 additions. Let an operation be a multiplication, division, addition, or subtraction. Strassen showed that the product of two matrices could be computed by < (4.7)«logl 7 opera- tions. The usual method for matrix multiplication requires 2n3 operations. Thus, (4.7)n'°g*7 < 2«3 if and only if n3-'oga7 > 2.35, i.e. if n > (2.35)5 « 100. Strassen uses block LDU factorization (Householder [2, p. 126]) recursively to compute the inverse of a matrix of order «22* by mlk divisions, g (6/5)m37* — mlk multiplications, and ;£ (6/5)(5 + m)m2lk — 7(m2k)2 additions. The inverse of a matrix of order n could then be computed by ^ (5.64)«logi'7 arithmetic operations. Let A as Axx AX2 Axx 0 1 Axx AX2 _A2X A22_ _A2X Ax 0 A 0 / where A = A22 — A2XAxx'1Al2, and / 0~ A~ = I Axx Ax2 An 0 _0 / 0 A"1 A%\ ^11 /_ Axx -- Axx Ax2 A A2XAX1 — Axx AX2 A -A^AnAÏÎ A-1 if Axx and A are nonsingular.
    [Show full text]