Development of CFD Thermal Hydraulics and Neutron Kinetics Coupling Methodologies for the Prediction of Local Safety Parameters for Light Water Reactors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Champion Brands to My Wife, Mercy the ‘Made in Germany’ Champion Brands Nation Branding, Innovation and World Export Leadership
The ‘Made in Germany’ Champion Brands To my wife, Mercy The ‘Made in Germany’ Champion Brands Nation Branding, Innovation and World Export Leadership UGESH A. JOSEPH First published 2013 by Gower Publishing Published 2016 by Routledge 2 Park Square, Milton Park, Abingdon, Oxon OX14 4RN 711 Third Avenue, New York, NY 10017, USA Routledge is an imprint of the Taylor & Francis Group, an informa business Copyright © Ugesh A. Joseph 2013 Ugesh A. Joseph has asserted his right under the Copyright, Designs and Patents Act, 1988, to be identified as the author of this work. Gower Applied Business Research Our programme provides leaders, practitioners, scholars and researchers with thought provoking, cutting edge books that combine conceptual insights, interdisciplinary rigour and practical relevance in key areas of business and management. All rights reserved. No part of this book may be reprinted or reproduced or utilised in any form or by any electronic, mechanical, or other means, now known or hereafter invented, including photocopying and recording, or in any information storage or retrieval system, without permission in writing from the publishers. Notice: Product or corporate names may be trademarks or registered trademarks, and are used only for identification and explanation without intent to infringe. British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library. The Library of Congress has cataloged the printed edition as follows: Joseph, Ugesh A. The ‘Made in Germany’ champion brands: nation branding, innovation and world export leadership / by Ugesh A. Joseph. pages cm Includes bibliographical references and index. ISBN 978-1-4094-6646-8 (hardback: alk. -

World Boxing Association
WORLD BOXING ASSOCIATION GILBERTO MENDOZA PRESIDENT OFFICIAL RATINGS AS OF AUGUST 2011 th th Based on results held from August 05 To August 29 , 2011 CHAIRMAN MEMBERS Edificio Ocean Business Plaza, Ave. JOSE OLIVER GOMEZ E-mail: [email protected] Aquilino de la Guardia con Calle 47, BARTOLOME TORRALBA (SPAIN) Oficina 1405, Piso 14 JOSE EMILIO GRAGLIA (A RGENTINA) Cdad. de Panamá, Panamá VICE CHAIRMAN ALAN KIM (KOREA) Phone: + (507) 340-6425 GEORG E MARTINEZ E-mail: [email protected] Web Site: www.wbanews.com HEAVYWEIGHT (Over 200 Lbs / 90.71 Kgs) CRUISERWEIGHT (200 Lbs / 90.71 Kgs) LIGHT HEAVYWEIGHT (175 Lbs / 79.38 Kgs) SUPER CHAMPION: WLADIMIR KLITSCHKO UKR World Champion: GUILLERMO JONES PAN World Cham pion: BEIBU T SHUMENOV KAZ World Champion: Won Title: 09- 27-08 Won Title: 01-29- 10 ALEXANDER POVETKIN RUS Last Mandatory: 10- 02-10 Last Mandatory: 07-23- 10 Won Title: 08-27-11 Last Defense: 10-02-10 Last Defense: 07-29-11 Last Mandatory: INTERIM CHAMPION: YOAN PABLO HERNANDEZ CUB Last Defense: IBF: STEVE CUNNINGHAM - WBO: MARCO HUCK WBC: BERNARD HOPKINS - IBF: TAVORIS CLOUD WBC: KRZYSZTOF WLODARCZYK WBC: VITALY KLITSCHKO - IBF:WLADIMIR KLITSCHKO WBO: NATHAN CLEVERLY WBO : WLADIMIR KLITSCHKO 1. HASIM RAHMAN USA 1. LATEEF KAYODE (NABA) NIG 1. GABRIEL CAMPILLO (OC) SPA 2. DAVID HAYE U.K. 2. PAWEL KOLODZIEJ (WBA INT) POL 2. GAYRAT AMEDOV (WB A INT) UZB 3. ROBERT HELENIUS (WBA I/C) FIN 3. OLA AFOLABI U.K. 3. DAWID KOSTECKY (WBA I/C) POL 4. ALEXANDER USTINO V (EBA) RUS 4. STEVE HERELIUS FRA 4. -

SERGIO MARTINEZ (ARGENTINA) WON TITLE: September 15, 2012 LAST DEFENCE: April 27, 2013 LAST COMPULSORY : September 15, 2012 by Chavez
WORLD BOXING COUNCIL R A T I N G S JULY 2013 José Sulaimán Chagnon President VICEPRESITENTS EXECUTIVE DIRECTOR TREASURER KOVID BHAKDIBHUMI, THAILAND CHARLES GILES, GREAT BRITAIN HOUCINE HOUICHI, TUNISIA MAURICIO SULAIMÁN, MEXICO JUAN SANCHEZ, USA REX WALKER, USA JU HWAN KIM, KOREA BOB LOGIST, BELGIUM LEGAL COUNSELORS EXECUTIVE LIFETIME HONORARY ROBERT LENHARDT, USA VICE PRESIDENTS Special Legal Councel to the Board of Governors JOHN ALLOTEI COFIE, GHANA of the WBC NEWTON CAMPOS, BRAZIL ALBERTO LEON, USA BERNARD RESTOUT, FRANCE BOBBY LEE, HAWAII YEWKOW HAYASHI, JAPAN Special Legal Councel to the Presidency of the WBC WORLD BOXING COUNCIL 2013 RATINGS JULY 2013 HEAVYWEIGHT +200 Lbs +90.71 Kgs VITALI KLITSCHKO (UKRAINE) WON TITLE: October 11, 2008 LAST DEFENCE: September 8, 2012 LAST COMPULSORY : September 10, 2011 WBA CHAMPION: Wladimir Klitschko Ukraine IBF CHAMPION: Wladimir Klitschko Ukraine WBO CHAMPION: Wladimir Klitschko Ukraine Contenders: WBC SILVER CHAMPION: Bermane Stiverne Canada WBC INT. CHAMPION: Seth Mitchell US 1 Bermane Stiverne (Canada) SILVER 2 Seth Mitchell (US) INTL 3 Chris Arreola (US) 4 Magomed Abdusalamov (Russia) USNBC 5 Tyson Fury (GB) 6 David Haye (GB) 7 Manuel Charr (Lebanon/Syria) INTL SILVER / MEDITERRANEAN/BALTIC 8 Kubrat Pulev (Bulgaria) EBU 9 Tomasz Adamek (Poland) 10 Johnathon Banks (US) 11 Fres Oquendo (P. Rico) 12 Franklin Lawrence (US) 13 Odlanier Solis (Cuba) 14 Eric Molina (US) NABF 15 Mark De Mori (Australia) 16 Luis Ortiz (Cuba) FECARBOX 17 Juan Carlos Gomez (Cuba) 18 Vyacheslav Glazkov (Ukraine) -

Ranking As of Sept. 10, 2012
Ranking as of Sept. 10, 2012 HEAVYWEIGHT JR. HEAVYWEIGHT LT. HEAVYWEIGHT (Over 201 lbs.)(Over 91,17 kgs) (200 lbs.)(90,72 kgs) (175 lbs.)(79,38 kgs) CHAMPION CHAMPION CHAMPION WLADIMIR KLITSCHKO (Sup Champ) UKR MARCO HUCK GER NATHAN CLEVERLY GB OLA AFOLABI (Interim) GB 1. Denis Boytsov RUS 1. BJ Flores USA 1. Robin Krasniqi (International) GER 2. Seth Mitchell (NABO) USA 2. Aleksandr Alekseev RUS 2. Braimah Kamoko (WBO Africa) GHA 3. David Haye (International) GB 3. Mateusz Masternak POL 3. Juergen Braehmer GER 4. Alexander Ustinov RUS 4. Nenad Borovcanin (WBO Europe Int.) SER 4. Dustin Dirks GER 5. Chris Arreola USA 5. Nuri Seferi (WBO Europe) ALB 5. Eduard Gutknecht GER 6. Carlos Takam (WBO Africa) CAM 6. Pawel Kolodziej POL 6. Bernard Hopkins USA 7. Luis Ortiz (Latino) CUB 7. Steve Cunningham USA 7. Vyacheslav Uzelkov (Int-Cont) UKR 8. Tyson Fury (Int-Cont) GB 8. Firat Arslan GER 8. Andrzej Fonfara POL 9. Robert Helenius FIN 9. Lateef Kayode NIG 9. Cornelius White USA 10. Francesco Pianeta ITA 10. Laudelino Barros (Latino) BRA 10. Karo Murat GER 11. Shane Cameron (Asia-Pac) (Oriental) NZ 11. Krzysztof Glowacki (Int-Cont) POL 11. Denis Simcic SVN 12. Sherman Williams (China)(Asia-Pac Int) BAH 12. Tony Conquest (International) GB 12. Jackson Junior (Latino) BRA 13. Kubrat Pulev BUL 13. Rakhim Chakhkiev RUS 13. Isaac Chilemba MAL 14. Joe Hanks USA 14. Danny Green AUST 14. Tony Bellew GB 15. Mariusz Wach POL 15. Agron Dzila SWI 15. Eleider Alvarez (NABO) COL CHAMPIONS CHAMPIONS CHAMPIONS WLADIMIR KLITSCHKO WBA GUILLERMO JONES WBA BEIBUT SHUMENOV WBA WLADIMIR KLITSCHKO IBF YOAN PABLO HERNANDEZ IBF TAVORIS CLOUD IBF VITALI KLITSCHKO WBC KRZYSZTOF WLODARCZYK WBC CHAD DAWSON WBC SUP. -

World Boxing Association Gilberto Mendoza
WORLD BOXING ASSOCIATION GILBERTO MENDOZA PRESIDENT OFFICIAL RATINGS AS OF NOVEMBER 2010 th th Based on results held from November 17 , 2010 to December 16 , 2010 MEMBERS CHAIRMAN Edificio Ocean Business Plaza, Ave. JOSE OLIVER GOMEZ E-mail: [email protected] BARTOLOME TORRALBA (SPAIN) Aquilino de la Guardia con Calle 47, JOSE EMILIO GRAGLIA (ARGENTINA) Oficina 1405, Piso 14 VICE CHAIRMAN Cdad. de Panamá, Panamá ALAN KIM (KOREA) Phone: + (507) 340-6425 GEORGE MARTINEZ E-mail: [email protected] GONZALO LOPEZ SILVERO (USA) Web Site: www.wbanews.com HEAVYWEIGHT (Over 200 Lbs / 90.71 Kgs) CRUISERWEIGHT (200 Lbs / 90.71 Kgs) LIGHT HEAVYWEIGHT (175 Lbs / 79.38 Kgs) World Champion: DAVID HAYE U.K. World Champion: GUILLERMO JONES PAN World Champion: BEIBUT SHUMENOV KAZ Won Title: 11-07-09 Won Title: 09-27-08 Won Title: 01-29-10 Last Mandatory: 04-03-10 Last Mandatory: 10-02-10 Last Mandatory: 07-23-10 Last Defense: 11-13-10 Last Defense: 10-02-10 Last Defense: 07-23-10 INTERIM CHAMPION: STEVE HERELIUS FRA WBC:VITALY KLITSCHKO- IBF:WLADIMIR KLITSCHKO IBF: STEVE CUNNINGHAM - WBO: MARCO HUCK WBC: JEAN PASCAL - IBF: TAVORIS CLOUD WBO : WLADIMIR KLITSCHKO WBC: KRZYSZTOF WLODARCZYK WBO: JURGEN BRAEHMER 1. RUSLAN CHAGAEV (OC) UZB 1. ALEXANDER FRENKEL GER 1. GABRIEL CAMPILLO (OC) SPA 2. DENNIS BOYTSOV (WBA I/C) RUS 2. YOAN PABLO HERNANDEZ CUB 2. ZOLT ERDEI HUN 3. ALEXANDER POVETKIN RUS 3. ALI ISMAILOV (PABA) AZE 3. VYACHESLAV UZELKOV UKR 4. ALEXANDER USTINOV (EBA) RUS 4. LATEEF KAYODE NIG 4. DAWID KOSTECKI POL 5. HASIM RAHMAN USA 5. -

Ranking As of Dec. 15, 2012
Ranking as of Dec. 15, 2012 HEAVYWEIGHT JR. HEAVYWEIGHT LT. HEAVYWEIGHT (Over 201 lbs.)(Over 91,17 kgs) (200 lbs.)(90,72 kgs) (175 lbs.)(79,38 kgs) CHAMPION CHAMPION CHAMPION WLADIMIR KLITSCHKO (Sup Champ) UKR MARCO HUCK GER NATHAN CLEVERLY GB OLA AFOLABI (Interim) GB 1. Robert Helenius FIN 1. BJ Flores (NABO) USA 1. Robin Krasniqi (International) GER 2. Denis Boytsov RUS 2. Aleksandr Alekseev RUS 2. Juergen Braehmer GER 3. David Haye (International) GB 3. Firat Arslan GER 3. Dustin Dirks GER 4. Chris Arreola USA 4. Mateusz Masternak POL 4. Braimah Kamoko (WBO Africa) GHA 5. Jonathon Banks (NABO) USA 5. Nuri Seferi (WBO Europe) ALB 5. Vyacheslav Uzelkov (Int-Cont) UKR 6. Tyson Fury (Int-Cont) GB 6. Steve Cunningham USA 6. Cornelius White USA 7. Luis Ortiz CUB 7. Lateef Kayode NIG 7. Karo Murat GER 8. Carlos Takam (WBO Africa) CAM 8. Krzysztof Glowacki (Int-Cont) POL 8. Andrzej Fonfara POL 9. Francesco Pianeta ITA 9. Laudelino Barros (Latino) BRA 9. Eduard Gutknecht GER 10. Shane Cameron (Asia-Pac.) (Oriental) NZ 10. Tony Conquest (International) GB 10. Bernard Hopkins USA 11. Kubrat Pulev BUL 11. Pawel Kolodziej POL 11. Marcus Vincinis De Oliveira BRA 12. Christian Hammer (WBO Europe) ROM 12. Rakhim Chakhkiev RUS 12. Isaac Chilemba MAL 13. Joe Hanks USA 13. Danny Green AUST 13. Jackson Junior (Latino) BRA 14. David Price GB 14. Dmytro Kucher UKR 14. Vikapita Meroro NAM 15. Andriy Rudenko UKR 15. Agron Dzila SWI 15. Eleider Alvarez (NABO) COL **Mark Flanagan (Oriental) AUST CHAMPIONS CHAMPIONS CHAMPIONS WLADIMIR KLITSCHKO WBA GUILLERMO JONES WBA BEIBUT SHUMENOV WBA WLADIMIR KLITSCHKO IBF YOAN PABLO HERNANDEZ IBF TAVORIS CLOUD IBF VITALI KLITSCHKO WBC KRZYSZTOF WLODARCZYK WBC CHAD DAWSON WBC SUP. -

Annual Report 2010 // Key Figures at a Glance
// fascinating people Annual Report 2010 // Key fiGureS at a Glance ProSiebenSat.1 Group: Key figures for 2010 EUR m Q4 2010 Q4 2009 Q4 20089) Q4 20078) Q4 2006 Revenue 954.1 880.4 876.8 989.3 657.2 Total costs 654.5 651.8 915.8 772.3 471.6 Recurring costs1) 599.9 576.2 621.6 695.1 460.3 Consumption of programming assets 311.2 290.1 327.5 395.6 264.2 Recurring EBITDA2) 358.6 307.2 279.3 296.9 200.8 Recurring EBITDA margin (in %) 37.6 34.9 31.9 30.0 30.6 EBITDA 338.9 293.0 251.7 281.1 200.2 Non-recurring items3) -19.7 -14.2 -27.6 -15.8 -0.6 EBIT 304.2 239.2 3.5 222.1 189.4 Financial result -65.1 -67.3 -133.3 -79.6 -11.0 Profit/loss before income taxes 239.0 171.9 -128.0 142.5 178.4 Consolidated net profit/loss (after non-controlling interests)4) 181.5 113.4 -170.0 39.5 113.4 Underlying net income5) 194.3 137.1 78.2 75.3 114.4 Investments in programming assets 279.6 267.8 329.3 366.9 261.1 EUR m 2010 2009 20089) 20078) 2006 Revenue 3,000.0 2,760.8 3,054.2 2,710.4 2,104.6 Total costs 2,341.7 2,310.7 2,851.0 2,341.9 1,672.4 Recurring costs1) 2,105.2 2,077.5 2,413.1 2,063.1 1,629.7 Consumption of programming assets 1,077.7 1,068.6 1,247.1 1,145.8 946.0 Recurring EBITDA2) 905.9 696.5 674.5 662.9 487.0 Recurring EBITDA margin (in %) 30.2 25.2 22.1 24.5 23.1 EBITDA 807.6 623.0 618.3 522.3 484.3 Non-recurring items3) -98.3 -73.5 -56.2 -140.6 -2.7 EBIT 669.6 475.1 263.5 385.3 444.3 Financial result -240.5 -242.47) -334.9 -135.5 -57.6 Profit/loss before income taxes 429.0 233.17) -68.4 249.8 386.7 Consolidated net profit/loss (after non-controlling -

The Irish Boxing Review
THE IRISH BOXING REVIEW 2013 EDITION STEVE WELLINGS Copyright © 2013 Steve Wellings All rights reserved. The scanning, uploading and distribution of this book via the Internet or any other means without the permission of the publisher is illegal and punishable by law. Please purchase only authorised electronic editions, and do not participate in or encourage electronic piracy of copyrighted materials. Your support of the author's rights is appreciated. Typeset by SML Publishing Services www.smlpubservices.com CONTENTS INTRODUCTION ‘Descending From Ireland’ by James Howard ‘It’s Been a Generally Positive Year for Our Fighters’ by David Mohan ‘Highs, Lows and Predictions – Boxing from 2012 to Present and Future’ by James Slater ‘The End for Hatton, But A New Beginning for Lennox Lewis’ by Marc Stockings ‘It’s Been An Enjoyable Year of Boxing’ by Paddy Appleton ‘Promoter Wars, Social Media Madness, Over-Hyped Prospects – Modern Day British Boxing in a Nut Shell’ by James Bairstow ‘McDonnell World Title Victory Was a Moment to Treasure’ by Jon Briggs ‘I Never Get Tired Writing About Boxing’ by Peter Wells ‘A Concise Review of Another Successful Year for Irish Amateur Boxing’ by Louis O’Meara ‘Let’s Look at the Current Standing of Some of the Most Significant Fighters on the Irish Boxing Scene Today’ by Jeremy O’Connell ‘Mike Stafford Will Be a Major Force Behind US Boxing Success’ by Jose Santana Jnr Irish Boxing News Round-Up – 15th January 2012 Rigondeaux Returns for Ramos Test − 16th January 2012 Fighter of the Year Magee Planning for Danish -
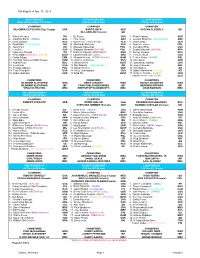
Ranking As of Apr. 10, 2013
Ranking as of Apr. 10, 2013 HEAVYWEIGHT JR. HEAVYWEIGHT LT. HEAVYWEIGHT (Over 201 lbs.)(Over 91,17 kgs) (200 lbs.)(90,72 kgs) (175 lbs.)(79,38 kgs) CHAMPION CHAMPION CHAMPION WLADIMIR KLITSCHKO (Sup Champ) UKR MARCO HUCK GER NATHAN CLEVERLY GB OLA AFOLABI (Interim) GB 1. Robert Helenius FIN 1. BJ Flores USA 1. Robin Krasniqi GER 2. Jonathon Banks (NABO) USA 2. Firat Arslan GER 2. Juergen Braehmer (International) GER 3. Denis Boytsov RUS 3. Nuri Seferi (WBO Europe) ALB 3. Dustin Dirks GER 4. David Haye (International) GB 4. Aleksandr Alekseev RUS 4. Andrzej Fonfara POL 5. Tyson Fury GB 5. Mateusz Masternak POL 5. Cornelius White USA 6. Luis Ortiz CUB 6. Krzysztof Glowacki (Int-Cont) POL 6. Doudou Ngumbu (Int-Cont) FRA 7. Francesco Pianeta ITA 7. Braimah Kamoko (WBO Africa) GHA 7. Sergey Kovalev RUS 8. Alex Leapai (Asia-Pac.) (Oriental) AUST 8. Laudelino Barros (Latino) BRA 8. Travoris Cloud USA 9. Carlos Takam CAM 9. Vikapita Meroro (WBO Africa Int.) NAM 9. Eleider Alvarez (NABO) COL 10. Christian Hammer (WBO Europe) ROM 10. Rakhim Chakhkiev RUS 10. Karo Murat GER 11. Kubrat Pulev BUL 11. Danny Green AUST 11. Vyacheslav Uzelkov UKR 12. Joe Hanks USA 12. Nell Dawson (International) GB 12. Isaac Chilemba MAL 13. Tomasz Adamek POL 13. Dmytro Kucher UKR 13. Tony Bellew GB 14. Tony Thompson USA 14. Steve Cunningham USA 14. Daniel MacKinnon (Oriental) NZ 15. Andriy Rudenko UKR 15. Brad Pitt AUST 15. Umberto Savigne (Latino) CUB ** Dominic Böesel (WBO Youth) GER CHAMPIONS CHAMPIONS CHAMPIONS WLADIMIR KLITSCHKO WBA DENIS LEBEDEV WBA BEIBUT SHUMENOV WBA WLADIMIR KLITSCHKO IBF YOAN PABLO HERNANDEZ IBF BERNARD HOPKINS IBF VITALI KLITSCHKO WBC KRZYSZTOF WLODARCZYK WBC CHAD DAWSON WBC SUP. -

WBA Continental Ranking February 2017
2017 Edificio Ocean Business Plaza, Ave. Aquilino de la Guardia con Calle 47, Oficina 1405, Piso 14 Cdad. de Panamá, Panamá Phone: + (507) 340-6425 Web Site: www.wbanews.com WORLD BOXING ASSOCIATION GILBERTO JESUS MENDOZA PRESIDENT OFFICIAL RATINGS AS OF FEBRUARY 2017 CHAIRMAN MEMBERS JESPER JENSEN DEN E-mail: [email protected] MARIANA BORISSOVA BUL THOMAS PUTZ GER PER AAKE PERSSON SWE Over HEAVYWEIGHT 200 Lbs / CRUISERWEIGHT 200 Lbs / LIGHT HEAVYWEIGHT 175 Lbs / 90.71 Kgs 90.71 Kgs 79.38 Kgs CONTINETAL CHAMPION ; CONTINENTAL CHAMPION : CONTINENTAL CHAMPION : VACANT VACANT DOMINIK BOESEL GER 1. WLADIMIR KLITSCHKO UKR 1. MARCO HUCK GER 2. ALEXANDER USTINOV RUS 2. ARSEN GOULAMARIAN ARM 1. DMITRY BIVOL RUS 3. DAVID HAYE UKR 3. MATZHEUS MASTERNAK ( WBA I/C ) POL 2. SERGEI KOVALEV RUS 4. MANUEL CHARR GER 4. NOEL GEVOR GER 3. ARTUR BETERBIEV RUS 5. KUBRAT PULEV BUL 5. RYAD MERHY BEL 4. JURGEN BRAEHMER GER 6. ANDREY FEDOSOV RUS 6. KRZYSTOF WLODARZYK POL 5. ENRICO KOELLING GER 7. DAVID PRICE GBR 7. MAKSIM VLASOV RUS 6. FRANK BUGLIONI GBR 8. ANTHONY JOSHUA GBR 8. RUSLAN FAYFER RUS 7. AVNI YILDIRIM TUR 9. ROBERT HELENIUS FIN 9. ISSA AKBERBAYEV KAZ 8. ERIK SKOGLUND SWE 10. HUGH FURY GBR 10. OLEKSANDER USYK UKR 9. ROBERT STIEGLITZ GER 11. JOHAN DUHAUPAS FRA 11. MICKI NIELSEN DEN 10. HAKIN ZOULIKA FRA 12. ALEXANDER POVETKIN RUS 12. DMITRY KUCHER RUS 11. KARO MURAT ARM 13. ADRIAN GRANAT SWE 13. KRZYSTOF GLOWACKI POL 12. MEHDI AMAR FRA 14. OTTO WALIN SWE 14. AGRON DZILA SUI 13. EMANUELLE BARLETTA ITA 14. -

Heavyweight Cruiserweight
WBA RATINGS COMMITTEE OCTOBER 2014 MOVEMENTS REPORT th th Based on results held from 05 October to November 12 , 2014 Miguel Prado Sanchez Chairman Gustavo Padilla Vice Chairman HEAVYWEIGHT DATE PLACE BOXER A RESULT BOXER B TITLE REMARKS 10-11-2014 Greenwich, U. K Anthony Joshua KOT2 Denis Bakhtov Vacant WBC Inter. C. Beloton 100-90 10-16-2014 Auckland, New Zealand Joseph Parker UD10 Sherman Williams PABA, WBO Oriental G. Borges 100-90 K. Bell 99-94 10-18-2014 Philadelphia, Pennsylvania Steve Cunningham TD 7 Natu Visina MOVEMENT OUT N° 3 Deontay Wilder goes out of the ratings because he is going to fight another organization title (WBC) IN Alexander Povetkin enters at position N° 3 at the criteria to the rating committee PROMOTIONS N° 11 Joseph Parker goes up to position N° 10 after defending his regional title successfully (PABA) DEMOTIONS N° 10 Antonio Tarver goes down to position N° 11 due to inactivity (334 days) CRUISERWEIGHT DATE PLACE BOXER A RESULT BOXER B TITLE REMARKS 10-18-2014 Now Dwor, Poland Krysztof Glowacki KO5 Thierry Kasrl WBO I/C 10-24-2014 Moscow, Russia Rakhim Chakhkiev KO4 Giacobbe Fragomeni Vacant EBU MOVEMENT OUT NOT CHANGES 1 IN NOT CHANGES PROMOTIONS NOT CHANGES DEMOTIONS NOT CHANGES LIGHT HEAVYWEIGHT DATE PLACE BOXER A RESULT BOXER B TITLE REMARKS B. Garry 60-53 10-03-2014 Tampa, Florida Radivoje Kalajdzic UD6 Rayco Saunders R. Green 60-53 J. O’connors 60-53 10-03-2014 Ardennes, France Mehdi Amar TD4 Jevgenijs Belitcenko 11-08-2014 Atlantic City, New Jersey Nadjib Mohammedi KO1 Demetrius Walker I. -

Strong Group of Mexican-Americans Carries on Enduring Tradition
LETTERS FROM EUROPE FROCH-KESSLER IS A COMPELLING REMATCH STRONG GROUP OF MEXICAN-AMERICANS CARRIES ON ENDURING TRADITION VICTOR ORTIZ ROBERT GUERRERO LEO SANTA CRUZ UNHAPPY RETURNS BOXERS OFTEN HAVE A TOUGH TIME STAYING RETIRED FATHER-SON ACT ANGEL GARCIA FIRES OFF WORDS, SON DANNY PUNCHES HOMECOMING MAY 2013 MAY SERGIO MARTINEZ RETURNS TO ARGENTINA A HERO TOO YOUNG TO DIE $8.95 OMAR HENRY NEVER HAD A CHANCE TO BLOSSOM CONTENTS / MAY 2013 38 64 70 FEATURES COVER STORY PACKAGE 58 | OVERSTAYED WELCOMES 76 | A LIFE CUT SHORT BOXERS HAVE A SELF-DESTRUCTIVE OMAR HENRY DIED OF CANCER BEFORE 38 | ENDURING TRADITION HABIT OF STICKING AROUND TOO LONG HE COULD REALIZE HIS POTENTIAL MEXICAN-AMERICAN BOXERS’ RECORD By Bernard Fernandez By Gary Andrew Poole OF SUCCESS CONTINUES By Don Stradley 64 | BARK AND BITE 82 | UNTAPPED SOURCE? ANGEL AND DANNY GARCIA ARE AN OLYMPIC CHAMPION 46 | NEW SHERIFF IN TOWN EFFECTIVE FATHER-SON TEAM ZOU SHIMING COULD MIKEY GARCIA’S BLEND OF POWER, By Ron Borges BE THE FIRST STAR SAVVY IS PROVING FORMIDABLE FROM CHINA 7O WELCOME HOME By Norm Frauenheim | By Tim Smith SERGIO MARTINEZ RETURNS TO 52 | BEST IN THE BIZ ARGENTINA A CONQUERING HERO TOP 10 MEXICAN-AMERICAN BOXERS By Bart Barry By Doug Fischer AT RINGTV.COM DEPARTMENTS 4 | RINGSIDE 94 | RINGSIDE REPORTS 5 | OPENING SHOTS 100 | WORLDWIDE RESULTS 10 | COME OUT WRITING 102 | COMING UP 11 | READY TO GRUMBLE 104 | NEW FACES: TERENCE CRAWFORD By David Greisman By Mike Coppinger 15 | ROLL WITH THE PUNCHES 106 | SIX PACK Jabs and Straight Writes by Thomas Hauser By T.K.