DOCSLIB.ORG

Minimum Mean Squared Error Estimation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Minimum Mean Squared Error Estimation MINIMUM MEAN SQUARED ERROR ESTIMATION by Victor Charles Drastik Submitted for the degree of Doctor of Philosophy, School of Mathematics, University of New South Wales. August, 1983 2. Abstract Let x1, x2, ... ,Xn be independent and identically distributed random variables, each with distribution depending on one or more para­ meters. The random vector ~ usually depends on a parameter e in a nonlinear fashion. We define a linearising transformation for e to be a function g(X) such that the dependence of g(X) on e is linear in the sense that E g(X) is proportional to e If we can find m · such transformations g1, g2 , .. ,gm we may construct an estimator of e as a compound linearising transformation A m e = . l c. g. ( X) 1 =1 1 1 - The optimal estimator of this form may then be found by minimising the mean squared error of e with respect to the constants c1, c2, ... ,cm. We will call the combination of these two stages the Method of Minimum Mean Squared Error Estimation. In this thesis, we discuss some approaches to finding linearising transformations. The resulting techniques are applied to several parametric problems, including a computer simulation study of estimators of scale parameters, in which a modification to the MLE is revealed to be almost optimal. Finally, we discuss distribution-free estimation of the centre of a syrrmetric distribution. I~ a computer simulation study, the estimators resulting from the MMSEE approach are found to be superior to the best estimators from the Princeton Robustness Study. 3. Acknowledgement I would like to express my gratitude to Dr. Peter Cooke, my supervisor and friend, whose guidance and encouragement have been of immeasurable value to me in the course of my research. 4. Contents Page Title Page 1 Abstract 2 Acknowledgement 3 Table of Contents 4 Notation 5 Chapter I In troduc ti on 8 Chapter II Theoretical Development 14 Chapter II I Scale Parameter Simulation Results 39 Chapter IV Distribution-free MMSEE 48 Appendix 74 Bibliography 76 5. Notation exp(x), ln(x) natural exponent and natural logarithm of x r(n) gamma function of n , defined as 00 n-1 -u r (n ) = J u e du for n > 0 0 B(m,n) beta function of m and n , defined as 1 B(m,n) = J um-1( 1-u )n-1 du= r(m)r(n) for 0 r(m+n) m > 0 , n > 0 n'. factori a 1 n , defined as n'. = r(n+l) for n -> 0 . When n is integral, n'. = n(n-1) ... 2.1 binomial coefficient of n and r , defined as (n) n'. f 0 r = r'. (n-r} '. or < r < n [xJ integer part of x , defined as the largest integer less than or equal to x the inverse function of h , defined as the value of x such that y = h(x) -X , A vector x , matrix A T X , AT transpose of ~, transpose of A J , l , n integration, summation, product operators a d ax , dx partial derivative, differentiation operators (f1 (x) = 1x f(x)) E , Var, Cov, MSE expectation, variance, covariance, mean squared error operators 6. random variable x. observed value of X. 1 1 x(l) ~ x(2) < ~ \n) order statistics based on x1, x2, ... ,Xn x(l) ~ x(2) < ordered observations sample mean, defined as = x x ln . 1 x.1 1= 1 1 n 2 s2 sample variance, defined as s2 = - l (X.-X) n-1 . 1 1= 1 F(xl~) cumulative distribution function of the random variable X, depending on the parameter vector e f(xl~) probability density function of the random variable X ~ depending on e 2 N(µ,o) Nonnal random variable with mean µ and variance o2 U[a,bJ Unifonn random variable over the interval [a,bJ a, a, y location, scale and shape parameters. <P, e lower, upper endpoints µ, a mean, standard deviation e,"' -e estimators of e C* quantity c distinguished in some way (usually optimal value of c) n sample size LT Linearising Transfonnation MLE Maximum Likelihood Estimation or Estimator or Estimate 7. MSE Mean Squared Error MMSEE Minimum MSE Estimation or Estjmator or Estimate V, E, ~ for all, belongs to, approximately equals is distributed as Character type use Lower case Greek scalars, parameters (Examples : w, µ) Lower case Roman vectors, constants or coefficients, observations, functions (Examples: C, a, X, f) Upper case Roman matrices, random variables, functions (Examples: A-1 , -X, F(x I~) ) Upper case Greek spaces, operators (Examples: 0, l: ) 8. Chapter I: Introduction In the classical problem of estimation of a single parameter e, the estimator is a function of independent and identically distributed random variables x1, x2, ... ,Xn each with distribution depending on e (and possibly other parameters). We would like to find an estimator ,.. e which is 11 close 11 to e . An ideal (or most concentrated) estimator is one which has its probability mass concentrated as closely as possible about the true parameter value e . Unfortunately, although the property of most concentrated is highly desirable, ideal estimators seldom exist. There are just too many possible estimators for any one of them to be most concentrated, so the concept of ideal estimation is not usable in practice. We need to find a criterion of closeness which also leads to estimators which are highly concentrated about e . The Mean Squared Error (MSE) of an estimator e(X) of the para­ meter e based on the sample ~ = (X 1, x2, ... ,Xn) is defined to be the average squared deviation of e from e and can be written as the ,.. variance of e plus the square of its bias; that is, MSE(e) = E{e(~)-e} 2 = Var(e) + {E(e-e)}2 The principal advantage of the MSE criterion is that it severely A penalises large deviations of e from e , that is, the frequency of large errors is greatly reduced. Another advantage is that consistency in MSE implies asymptotic unbiasedness and consistency in probability. Asymptotically the estimator is concentrated arbitrarily closely to e (but perhaps not optimally so). 9. Let 0 represent the set of all possible estimators e of e. A A uniformly MSE-optimal estimator among all members of 0 cannot exist because 0 is too large. It includes estimators such as 8(X)-- = 0 V X which are extremely prejudiced in favour of a particular e value. Therefore an estimator which has uniformly smallest MSE would necessarily have zero MSE for all e . This is clearly impossible except for trivial cases. We must therefore restrict our attention to some suitable subset of 0. The estimators in such a subset should possess some desirable property, usually by satisfying a constraint equation. The two most corrmon constraints are (1) unbiasedness, with constraint equation E(e) = e V0E0 and (2) invariance, expressed as location: 8( X+c) = 0(X) + C scale e(cX) = ea( X) 1 V -X , V c ER The MSE-optimal estimators in the first subset are Uniformly Minimum Variance Unbiased Estimators and in the second are Pitman [16J estimators of location and scale. In this thesis we consider estimators in a third subset of 0 that defined by the constraint m a(X) = l c. g.(X) 1=. 1 1 1 - where {ci} is a set of undetermined coefficients and {gi} is a set of functions of the sample data. This constraint has the advantage 10. that, unlike the other constraints, it immediately gives us a functional fonn for the estimator. Like the others it is not a strong restriction and often the three methods develop fonnulae which differ only in constants. Another advantage is that once the functions {gi} are chosen, the selection of the MSE-optimal member of the set is usually a matter of some elementary calculus, whereas the optimal estimators for the other methods are not at all obvious. The Method of Minimum Mean Squared Error Estimation (MMSEE) is one of a class of methods of optimal algorithm selection generally known as "methods of undetennined coefficients" (see, for example, Gerald, [BJ). The principle behind these methods is that first we choose a class of formulae that are likely to be effective in solving a given problem, then we choose a particular member of the class by referring to some appropriate criterion of efficiency. For example, a problem in numerical analysis is to find the area under a curve between two given points by approximate integration. The method of undetennined coef­ ficients used by Gauss to solve this problem is as follows: first we select a class of fonnulae by considering the characteristics of the problem. We can write the value of the integral as b I = f f(x)dx = (b-a)f a where f is the average value of f over the domain [a,bJ. One reasonable fonnula to approximate an average function value is a linear combination of several function values. Thus " m I = w. f(x .) . l 1 , 1 1= is an approximation to I , where {xi} is a set of points in [a,bJ and {wi} is a set of undetermined coefficients. Next, we select a 11. criterion for deciding which "I is the best one for our purposes. There are several reasonable criteria available, but the one usually chosen is that I should be exact for as many low-order polynomials as possible. Since we have 2m undetermined quantities, it must be " possible to choose the {wi} and {xi} such that I correctly evaluates the integrals of all polynomials of degree less than or equal to 2m-1 • Thus, in general, in order to select a class of formulae, we apply some prior knowledge about what sort of formula is.likely to be suit­ able.
Load more

Recommended publications
  • Lecture 13: Simple Linear Regression in Matrix Format
    11:55 Wednesday 14th October, 2015 See updates and corrections at http://www.stat.cmu.edu/~cshalizi/mreg/ Lecture 13: Simple Linear Regression in Matrix Format 36-401, Section B, Fall 2015 13 October 2015 Contents 1 Least Squares in Matrix Form 2 1.1 The Basic Matrices . .2 1.2 Mean Squared Error . .3 1.3 Minimizing the MSE . .4 2 Fitted Values and Residuals 5 2.1 Residuals . .7 2.2 Expectations and Covariances . .7 3 Sampling Distribution of Estimators 8 4 Derivatives with Respect to Vectors 9 4.1 Second Derivatives . 11 4.2 Maxima and Minima . 11 5 Expectations and Variances with Vectors and Matrices 12 6 Further Reading 13 1 2 So far, we have not used any notions, or notation, that goes beyond basic algebra and calculus (and probability). This has forced us to do a fair amount of book-keeping, as it were by hand. This is just about tolerable for the simple linear model, with one predictor variable. It will get intolerable if we have multiple predictor variables. Fortunately, a little application of linear algebra will let us abstract away from a lot of the book-keeping details, and make multiple linear regression hardly more complicated than the simple version1. These notes will not remind you of how matrix algebra works. However, they will review some results about calculus with matrices, and about expectations and variances with vectors and matrices. Throughout, bold-faced letters will denote matrices, as a as opposed to a scalar a. 1 Least Squares in Matrix Form Our data consists of n paired observations of the predictor variable X and the response variable Y , i.e., (x1; y1);::: (xn; yn).
    [Show full text]
  • In This Segment, We Discuss a Little More the Mean Squared Error
    MITOCW | MITRES6_012S18_L20-04_300k In this segment, we discuss a little more the mean squared error. Consider some estimator. It can be any estimator, not just the sample mean. We can decompose the mean squared error as a sum of two terms. Where does this formula come from? Well, we know that for any random variable Z, this formula is valid. And if we let Z be equal to the difference between the estimator and the value that we're trying to estimate, then we obtain this formula here. The expected value of our random variable Z squared is equal to the variance of that random variable plus the square of its mean. Let us now rewrite these two terms in a more suggestive way. We first notice that theta is a constant. When you add or subtract the constant from a random variable, the variance does not change. So this term is the same as the variance of theta hat. This quantity here, we will call it the bias of the estimator. It tells us whether theta hat is systematically above or below than the unknown parameter theta that we're trying to estimate. And using this terminology, this term here is just equal to the square of the bias. So the mean squared error consists of two components, and these capture different aspects of an estimator's performance. Let us see what they are in a concrete setting. Suppose that we're estimating the unknown mean of some distribution, and that our estimator is the sample mean. In this case, the mean squared error is the variance, which we know to be sigma squared over n, plus the bias term.
    [Show full text]
  • Minimum Mean Squared Error Model Averaging in Likelihood Models
    Statistica Sinica 26 (2016), 809-840 doi:http://dx.doi.org/10.5705/ss.202014.0067 MINIMUM MEAN SQUARED ERROR MODEL AVERAGING IN LIKELIHOOD MODELS Ali Charkhi1, Gerda Claeskens1 and Bruce E. Hansen2 1KU Leuven and 2University of Wisconsin, Madison Abstract: A data-driven method for frequentist model averaging weight choice is developed for general likelihood models. We propose to estimate the weights which minimize an estimator of the mean squared error of a weighted estimator in a local misspecification framework. We find that in general there is not a unique set of such weights, meaning that predictions from multiple model averaging estimators might not be identical. This holds in both the univariate and multivariate case. However, we show that a unique set of empirical weights is obtained if the candidate models are appropriately restricted. In particular a suitable class of models are the so-called singleton models where each model only includes one parameter from the candidate set. This restriction results in a drastic reduction in the computational cost of model averaging weight selection relative to methods which include weights for all possible parameter subsets. We investigate the performance of our methods in both linear models and generalized linear models, and illustrate the methods in two empirical applications. Key words and phrases: Frequentist model averaging, likelihood regression, local misspecification, mean squared error, weight choice. 1. Introduction We study a focused version of frequentist model averaging where the mean squared error plays a central role. Suppose we have a collection of models S 2 S to estimate a population quantity µ, this is the focus, leading to a set of estimators fµ^S : S 2 Sg.
    [Show full text]
  • Calibration: Calibrate Your Model
    DUE TODAYCOMPUTER FILES AND QUESTIONS for Assgn#6 Assignment # 6 Steady State Model Calibration: Calibrate your model. If you want to conduct a transient calibration, talk with me first. Perform calibration using UCODE. Be sure your report addresses global, graphical, and spatial measures of error as well as common sense. Consider more than one conceptual model and compare the results. Remember to make a prediction with your calibrated models and evaluate confidence in your prediction. Be sure to save your files because you will want to use them later in the semester. Suggested Calibration Report Outline Title Introduction describe the system to be calibrated (use portions of your previous report as appropriate) Observations to be matched in calibration type of observations locations of observations observed values uncertainty associated with observations explain specifically what the observation will be matched to in the model Calibration Procedure Evaluation of calibration residuals parameter values quality of calibrated model Calibrated model results Predictions Uncertainty associated with predictions Problems encountered, if any Comparison with uncalibrated model results Assessment of future work needed, if appropriate Summary/Conclusions Summary/Conclusions References submit the paper as hard copy and include it in your zip file of model input and output submit the model files (input and output for both simulations) in a zip file labeled: ASSGN6_LASTNAME.ZIP Calibration (Parameter Estimation, Optimization, Inversion, Regression) adjusting parameter values, boundary conditions, model conceptualization, and/or model construction until the model simulation matches field observations We calibrate because 1. the field measurements are not accurate reflecti ons of the model scale properties, and 2.
    [Show full text]
  • Bayes Estimator Recap - Example
    Recap Bayes Risk Consistency Summary Recap Bayes Risk Consistency Summary . Last Lecture . Biostatistics 602 - Statistical Inference Lecture 16 • What is a Bayes Estimator? Evaluation of Bayes Estimator • Is a Bayes Estimator the best unbiased estimator? . • Compared to other estimators, what are advantages of Bayes Estimator? Hyun Min Kang • What is conjugate family? • What are the conjugate families of Binomial, Poisson, and Normal distribution? March 14th, 2013 Hyun Min Kang Biostatistics 602 - Lecture 16 March 14th, 2013 1 / 28 Hyun Min Kang Biostatistics 602 - Lecture 16 March 14th, 2013 2 / 28 Recap Bayes Risk Consistency Summary Recap Bayes Risk Consistency Summary . Recap - Bayes Estimator Recap - Example • θ : parameter • π(θ) : prior distribution i.i.d. • X1, , Xn Bernoulli(p) • X θ fX(x θ) : sampling distribution ··· ∼ | ∼ | • π(p) Beta(α, β) • Posterior distribution of θ x ∼ | • α Prior guess : pˆ = α+β . Joint fX(x θ)π(θ) π(θ x) = = | • Posterior distribution : π(p x) Beta( xi + α, n xi + β) | Marginal m(x) | ∼ − • Bayes estimator ∑ ∑ m(x) = f(x θ)π(θ)dθ (Bayes’ rule) | α + x x n α α + β ∫ pˆ = i = i + α + β + n n α + β + n α + β α + β + n • Bayes Estimator of θ is ∑ ∑ E(θ x) = θπ(θ x)dθ | θ Ω | ∫ ∈ Hyun Min Kang Biostatistics 602 - Lecture 16 March 14th, 2013 3 / 28 Hyun Min Kang Biostatistics 602 - Lecture 16 March 14th, 2013 4 / 28 Recap Bayes Risk Consistency Summary Recap Bayes Risk Consistency Summary . Loss Function Optimality Loss Function Let L(θ, θˆ) be a function of θ and θˆ.
    [Show full text]
  • An Analysis of Random Design Linear Regression
    An Analysis of Random Design Linear Regression Daniel Hsu1,2, Sham M. Kakade2, and Tong Zhang1 1Department of Statistics, Rutgers University 2Department of Statistics, Wharton School, University of Pennsylvania Abstract The random design setting for linear regression concerns estimators based on a random sam- ple of covariate/response pairs. This work gives explicit bounds on the prediction error for the ordinary least squares estimator and the ridge regression estimator under mild assumptions on the covariate/response distributions. In particular, this work provides sharp results on the \out-of-sample" prediction error, as opposed to the \in-sample" (fixed design) error. Our anal- ysis also explicitly reveals the effect of noise vs. modeling errors. The approach reveals a close connection to the more traditional fixed design setting, and our methods make use of recent ad- vances in concentration inequalities (for vectors and matrices). We also describe an application of our results to fast least squares computations. 1 Introduction In the random design setting for linear regression, one is given pairs (X1;Y1);:::; (Xn;Yn) of co- variates and responses, sampled from a population, where each Xi are random vectors and Yi 2 R. These pairs are hypothesized to have the linear relationship > Yi = Xi β + i for some linear map β, where the i are noise terms. The goal of estimation in this setting is to find coefficients β^ based on these (Xi;Yi) pairs such that the expected prediction error on a new > 2 draw (X; Y ) from the population, measured as E[(X β^ − Y ) ], is as small as possible.
    [Show full text]
  • Review of Basic Statistics and the Mean Model for Forecasting
    Review of basic statistics and the simplest forecasting model: the sample mean Robert Nau Fuqua School of Business, Duke University August 2014 Most of what you need to remember about basic statistics Consider a random variable called X that is a time series (a set of observations ordered in time) consisting of the following 20 observations: 114, 126, 123, 112, 68, 116, 50, 108, 163, 79, 67, 98, 131, 83, 56, 109, 81, 61, 90, 92. 180 160 140 120 100 80 60 40 20 0 0 5 10 15 20 25 How should we forecast what will happen next? The simplest forecasting model that we might consider is the mean model,1 which assumes that the time series consists of independently and identically distributed (“i.i.d.”) values, as if each observation is randomly drawn from the same population. Under this assumption, the next value should be predicted to be equal to the historical sample mean if the goal is to minimize mean squared error. This might sound trivial, but it isn’t. If you understand the details of how this works, you are halfway to understanding linear regression. (No kidding: see section 3 of the regression notes handout.) To set the stage for using the mean model for forecasting, let’s review some of the most basic concepts of statistics. Let: X = a random variable, with its individual values denoted by x1, x2, etc. N = size of the entire population of values of X (possibly infinite)2 n = size of a finite sample of X 1 This might also be called a “constant model” or an “intercept-only regression.” 2 The term “population” does not refer to the number of distinct values of X.
    [Show full text]
  • Linear Regression
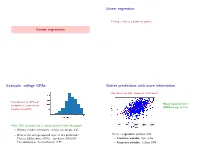
    Linear regression Fitting a line to a bunch of points. Linear regression Example: college GPAs Better predictions with more information We also have SAT scores of all students. Distribution of GPAs of Mean squared error students at a certain Ivy (MSE) drops to 0.43. League university. What GPA to predict for a random student from this group? • Without further information, predict the mean, 2.47. • What is the average squared error of this prediction? This is a regression problem with: 2 That is, E[((student's GPA) − (predicted GPA)) ]? • Predictor variable: SAT score The variance of the distribution, 0.55. • Response variable: College GPA Parametrizing a line The line fitting problem (1) (1) (n) (n) Pick a line (a; b) based on (x ; y );:::; (x ; y ) 2 R × R A line can be parameterized as y = ax + b (a: slope, b: intercept). • x(i); y (i) are predictor and response variables. E.g. SAT score, GPA of ith student. • Minimize the mean squared error, n 1 X MSE(a; b) = (y (i) − (ax(i) + b))2: n i=1 This is the loss function. Minimizing the loss function Multivariate regression: diabetes study Given (x(1); y (1));:::; (x(n); y (n)), minimize n Data from n = 442 diabetes patients. X L(a; b) = (y (i) − (ax(i) + b))2: i=1 For each patient: • 10 features x = (x1;:::; x10) age, sex, body mass index, average blood pressure, and six blood serum measurements. • A real value y: the progression of the disease a year later. Regression problem: • response y 2 R 10 • predictor variables x 2 R Least-squares regression Back to the diabetes data 10 Linear function of 10 variables: for x 2 R , • No predictor variables: mean squared error (MSE) = 5930 f (x) = w1x1 + w2x2 + ··· + w10x10 + b = w · x + b • One predictor ('bmi'): MSE = 3890 where w = (w1; w2;:::; w10).
    [Show full text]
  • Lecture 9 Estimators
    Lecture 9: Estimators 1 of 13 Course: Mathematical Statistics Term: Fall 2018 Instructor: Gordan Žitkovi´c Lecture 9 Estimators We defined an estimator as any function of the data which is not allowed to depend on the value of the unknown parameters. Such a broad definition allows for very silly examples. To rule out bad estimators and to find the ones that will provide us with the most “bang for the buck”, we need to discuss, first, what it means for an estimator to be “good”. There is no one answer to this question, and a large part of entire discipline (decision theory) tries to answer it. Some desirable properties of estimators are, however, hard to argue with, so we start from those. 9.1 Unbiased estimators Definition 9.1.1. We say that an estimator qˆ is unbiased for the pa- rameter q if E[qˆ] = q. We also define the bias E[qˆ] − q of qˆ, and denote it by bias(qˆ). In words, qˆ is unbiased if we do not expect qˆ to be systematically above or systematically below q. Clearly, in order to talk about the bias of an estimator, we need to specify what that estimator is trying to estimate. We will see below that same estimator can be unbiased as an estimator for one parameter, but biased when used to estimate another parameter. Another important question that needs to be asked about Definition 9.1.1 above is: what does it mean to take the expected value of qˆ, when we do not know what its distribution is.
    [Show full text]
  • MS&E 226: Fundamentals of Data Science
    MS&E 226: Fundamentals of Data Science Lecture 6: Bias and variance Ramesh Johari 1 / 49 Our plan today In general, when creating predictive models, we are trading off two different goals: I On one hand, we want models to fit the training data well. I On the other hand, we want to avoid models that become so finely tuned to the training data that they perform poorly on new data. In this lecture we develop a systematic vocabulary for talking about this kind of trade off, through the notions of bias and variance. 2 / 49 Conditional expectation 3 / 49 Conditional expectation Given the population model for X~ and Y , suppose we are allowed to choose any predictive model f^ we want. What is the best one? ^ ~ 2 minimize EX;Y~ [(Y − f(X)) ]: (Here expectation is over (X;Y~ ).) Theorem The predictive model that minimizes squared error is ^ ~ ~ f(X) = EY [Y jX]. 4 / 49 Conditional expectation Proof: ^ ~ 2 EX;Y~ [(Y − f(X)) ] ~ ~ ^ ~ 2 = EX;Y~ [(Y − EY [Y jX] + EY [Y jX] − f(X)) ] ~ 2 ~ ^ ~ 2 = EX;Y~ [(Y − EY [Y jX]) ] + EY [(E[Y jX] − f(X)) ] ~ ~ ^ ~ + 2EX;Y~ [(Y − EY [Y jX])(EY [Y jX] − f(X))]: The first two terms are positive, and minimized if ^ ~ ~ f(X) = EY [Y jX]. For the third term, using the tower property of conditional expectation: ~ ~ ^ ~ EX;Y~ [(Y − EY [Y jX])(EY [Y jX] − f(X))] h ~ ~ ~ ^ ~ i = EX~ EY [Y − EY [Y jX]jX](EY [Y jX] − f(X)) = 0: So the squared error minimizing solution is to choose ^ ~ ~ f(X) = EY [Y jX].
    [Show full text]
  • R2 Is Rescaled Mean Squared Error
    R2 is rescaled mean squared error Brendan O’Connor September 3, 2009 R2 – “the coefficient of determination” – is a rescaling of MSE (relative to the dataset in question). Alternative definitions are (1) the regression’s proportion of total sum of squares, or (2) the squared correlation between predictions and responses. Setup: items xi and we’re targeting real-valued responses yi by fitting a function f(x). Let’s be vague on training vs. test sets; all that matters is we want to evaluate the prediction function’s accuracy on these items. Then 2 MSE = X(f(xi) − yi) /N i Let’s use definition #1 of (1−R2), that it’s the “sum of squared error divided by total sum of squares”. These terms are 2 • SStot = (yi −E[y]) : total sum of squares, which is a rescaling of response variance 2 • SSerr = (yi−f(xi)) : sum of squared errors, a.k.a. “residual sum of squares”, a rescaling of the model’s predictions’ MSE So we have: 2 SSerr 1 − R = SStot − 2 P(yi f(xi)) /N = − 2 P(yi E[y]) /N MSE = V ar(y) (Mean)SqErr of predictions = (Mean)SqErr of guessing the mean R2 can be thought of as a rescaling of MSE, comparing it to the variance of the outcome response. It’s nice to interpret because it’s bounded between 0 and 1. Higher is better. If MSE=0, then R2 = 100%: you have perfect predictions. 1 If MSE is as bad as just guessing the mean for everything, then R2 = 0%: about as bad as possible.
    [Show full text]
  • A Simulation Study of the Robustness of the Least Median of Squares Estimator of Slope in a Regression Through the Origin Model
    A SIMULATION STUDY OF THE ROBUSTNESS OF THE LEAST MEDIAN OF SQUARES ESTIMATOR OF SLOPE IN A REGRESSION THROUGH THE ORIGIN MODEL by THILANKA DILRUWANI PARANAGAMA B.Sc., University of Colombo, Sri Lanka, 2005 A REPORT submitted in partial fulfillment of the requirements for the degree MASTER OF SCIENCE Department of Statistics College of Arts and Sciences KANSAS STATE UNIVERSITY Manhattan, Kansas 2010 Approved by: Major Professor Dr. Paul Nelson Abstract The principle of least squares applied to regression models estimates parameters by minimizing the mean of squared residuals. Least squares estimators are optimal under normality but can perform poorly in the presence of outliers. This well known lack of robustness motivated the development of alternatives, such as least median of squares estimators obtained by minimizing the median of squared residuals. This report uses simulation to examine and compare the robustness of least median of squares estimators and least squares estimators of the slope of a regression line through the origin in terms of bias and mean squared error in a variety of conditions containing outliers created by using mixtures of normal and heavy tailed distributions. It is found that least median of squares estimation is almost as good as least squares estimation under normality and can be much better in the presence of outliers. Table of Contents List of Figures ................................................................................................................................ iv List of Tables .................................................................................................................................
    [Show full text]