A Novel Lossless Encoding Algorithm for Data Compression
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Package 'Brotli'
Package ‘brotli’ May 13, 2018 Type Package Title A Compression Format Optimized for the Web Version 1.2 Description A lossless compressed data format that uses a combination of the LZ77 algorithm and Huffman coding. Brotli is similar in speed to deflate (gzip) but offers more dense compression. License MIT + file LICENSE URL https://tools.ietf.org/html/rfc7932 (spec) https://github.com/google/brotli#readme (upstream) http://github.com/jeroen/brotli#read (devel) BugReports http://github.com/jeroen/brotli/issues VignetteBuilder knitr, R.rsp Suggests spelling, knitr, R.rsp, microbenchmark, rmarkdown, ggplot2 RoxygenNote 6.0.1 Language en-US NeedsCompilation yes Author Jeroen Ooms [aut, cre] (<https://orcid.org/0000-0002-4035-0289>), Google, Inc [aut, cph] (Brotli C++ library) Maintainer Jeroen Ooms <[email protected]> Repository CRAN Date/Publication 2018-05-13 20:31:43 UTC R topics documented: brotli . .2 Index 4 1 2 brotli brotli Brotli Compression Description Brotli is a compression algorithm optimized for the web, in particular small text documents. Usage brotli_compress(buf, quality = 11, window = 22) brotli_decompress(buf) Arguments buf raw vector with data to compress/decompress quality value between 0 and 11 window log of window size Details Brotli decompression is at least as fast as for gzip while significantly improving the compression ratio. The price we pay is that compression is much slower than gzip. Brotli is therefore most effective for serving static content such as fonts and html pages. For binary (non-text) data, the compression ratio of Brotli usually does not beat bz2 or xz (lzma), however decompression for these algorithms is too slow for browsers in e.g. -
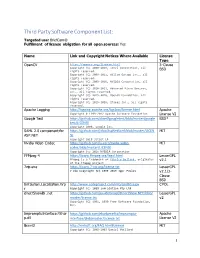
Third Party Software Component List: Targeted Use: Briefcam® Fulfillment of License Obligation for All Open Sources: Yes
Third Party Software Component List: Targeted use: BriefCam® Fulfillment of license obligation for all open sources: Yes Name Link and Copyright Notices Where Available License Type OpenCV https://opencv.org/license.html 3-Clause Copyright (C) 2000-2019, Intel Corporation, all BSD rights reserved. Copyright (C) 2009-2011, Willow Garage Inc., all rights reserved. Copyright (C) 2009-2016, NVIDIA Corporation, all rights reserved. Copyright (C) 2010-2013, Advanced Micro Devices, Inc., all rights reserved. Copyright (C) 2015-2016, OpenCV Foundation, all rights reserved. Copyright (C) 2015-2016, Itseez Inc., all rights reserved. Apache Logging http://logging.apache.org/log4cxx/license.html Apache Copyright © 1999-2012 Apache Software Foundation License V2 Google Test https://github.com/abseil/googletest/blob/master/google BSD* test/LICENSE Copyright 2008, Google Inc. SAML 2.0 component for https://github.com/jitbit/AspNetSaml/blob/master/LICEN MIT ASP.NET SE Copyright 2018 Jitbit LP Nvidia Video Codec https://github.com/lu-zero/nvidia-video- MIT codec/blob/master/LICENSE Copyright (c) 2016 NVIDIA Corporation FFMpeg 4 https://www.ffmpeg.org/legal.html LesserGPL FFmpeg is a trademark of Fabrice Bellard, originator v2.1 of the FFmpeg project 7zip.exe https://www.7-zip.org/license.txt LesserGPL 7-Zip Copyright (C) 1999-2019 Igor Pavlov v2.1/3- Clause BSD Infralution.Localization.Wp http://www.codeproject.com/info/cpol10.aspx CPOL f Copyright (C) 2018 Infralution Pty Ltd directShowlib .net https://github.com/pauldotknopf/DirectShow.NET/blob/ LesserGPL -

The Perceptual Impact of Different Quantization Schemes in G.719
The perceptual impact of different quantization schemes in G.719 BOTE LIU Master’s Degree Project Stockholm, Sweden May 2013 XR-EE-SIP 2013:001 Abstract In this thesis, three kinds of quantization schemes, Fast Lattice Vector Quantization (FLVQ), Pyramidal Vector Quantization (PVQ) and Scalar Quantization (SQ) are studied in the framework of audio codec G.719. FLVQ is composed of an RE8 -based low-rate lattice vector quantizer and a D8 -based high-rate lattice vector quantizer. PVQ uses pyramidal points in multi-dimensional space and is very suitable for the compression of Laplacian-like sources generated from transform. SQ scheme applies a combination of uniform SQ and entropy coding. Subjective tests of these three versions of audio codecs show that FLVQ and PVQ versions of audio codecs are both better than SQ version for music signals and SQ version of audio codec performs well on speech signals, especially for male speakers. I Acknowledgements I would like to express my sincere gratitude to Ericsson Research, which provides me with such a good thesis work to do. I am indebted to my supervisor, Sebastian Näslund, for sparing time to communicate with me about my work every week and giving me many valuable suggestions. I am also very grateful to Volodya Grancharov and Eric Norvell for their advice and patience as well as consistent encouragement throughout the thesis. My thanks are extended to some other Ericsson researchers for attending the subjective listening evaluation in the thesis. Finally, I want to thank my examiner, Professor Arne Leijon of Royal Institute of Technology (KTH) for reviewing my report very carefully and supporting my work very much. -

Compressed Transitive Delta Encoding 1. Introduction
Compressed Transitive Delta Encoding Dana Shapira Department of Computer Science Ashkelon Academic College Ashkelon 78211, Israel [email protected] Abstract Given a source file S and two differencing files ∆(S; T ) and ∆(T;R), where ∆(X; Y ) is used to denote the delta file of the target file Y with respect to the source file X, the objective is to be able to construct R. This is intended for the scenario of upgrading soft- ware where intermediate releases are missing, or for the case of file system backups, where non consecutive versions must be recovered. The traditional way is to decompress ∆(S; T ) in order to construct T and then apply ∆(T;R) on T and obtain R. The Compressed Transitive Delta Encoding (CTDE) paradigm, introduced in this paper, is to construct a delta file ∆(S; R) working directly on the two given delta files, ∆(S; T ) and ∆(T;R), without any decompression or the use of the base file S. A new algorithm for solving CTDE is proposed and its compression performance is compared against the traditional \double delta decompression". Not only does it use constant additional space, as opposed to the traditional method which uses linear additional memory storage, but experiments show that the size of the delta files involved is reduced by 15% on average. 1. Introduction Differential file compression represents a target file T with respect to a source file S. That is, both the encoder and decoder have available identical copies of S. A new file T is encoded and subsequently decoded by making use of S. -

Table of Contents Modules and Packages
Table of Contents Modules and Packages...........................................................................................1 Software on NAS Systems..................................................................................................1 Using Software Packages in pkgsrc...................................................................................4 Using Software Modules....................................................................................................7 Modules and Packages Software on NAS Systems UPDATE IN PROGRESS: Starting with version 2.17, SGI MPT is officially known as HPE MPT. Use the command module load mpi-hpe/mpt to get the recommended version of MPT library on NAS systems. This article is being updated to reflect this change. Software programs on NAS systems are managed as modules or packages. Available programs are listed in tables below. Note: The name of a software module or package may contain additional information, such as the vendor name, version number, or what compiler/library is used to build the software. For example: • comp-intel/2016.2.181 - Intel Compiler version 2016.2.181 • mpi-sgi/mpt.2.15r20 - SGI MPI library version 2.15r20 • netcdf/4.4.1.1_mpt - NetCDF version 4.4.1.1, built with SGI MPT Modules Use the module avail command to see all available software modules. Run module whatis to view a short description of every module. For more information about a specific module, run module help modulename. See Using Software Modules for more information. Available Modules (as -

Implementing Compression on Distributed Time Series Database
Implementing compression on distributed time series database Michael Burman School of Science Thesis submitted for examination for the degree of Master of Science in Technology. Espoo 05.11.2017 Supervisor Prof. Kari Smolander Advisor Mgr. Jiri Kremser Aalto University, P.O. BOX 11000, 00076 AALTO www.aalto.fi Abstract of the master’s thesis Author Michael Burman Title Implementing compression on distributed time series database Degree programme Major Computer Science Code of major SCI3042 Supervisor Prof. Kari Smolander Advisor Mgr. Jiri Kremser Date 05.11.2017 Number of pages 70+4 Language English Abstract Rise of microservices and distributed applications in containerized deployments are putting increasing amount of burden to the monitoring systems. They push the storage requirements to provide suitable performance for large queries. In this paper we present the changes we made to our distributed time series database, Hawkular-Metrics, and how it stores data more effectively in the Cassandra. We show that using our methods provides significant space savings ranging from 50 to 95% reduction in storage usage, while reducing the query times by over 90% compared to the nominal approach when using Cassandra. We also provide our unique algorithm modified from Gorilla compression algorithm that we use in our solution, which provides almost three times the throughput in compression with equal compression ratio. Keywords timeseries compression performance storage Aalto-yliopisto, PL 11000, 00076 AALTO www.aalto.fi Diplomityön tiivistelmä Tekijä Michael Burman Työn nimi Pakkausmenetelmät hajautetussa aikasarjatietokannassa Koulutusohjelma Pääaine Computer Science Pääaineen koodi SCI3042 Työn valvoja ja ohjaaja Prof. Kari Smolander Päivämäärä 05.11.2017 Sivumäärä 70+4 Kieli Englanti Tiivistelmä Hajautettujen järjestelmien yleistyminen on aiheuttanut valvontajärjestelmissä tiedon määrän kasvua, sillä aikasarjojen määrä on kasvanut ja niihin talletetaan useammin tietoa. -

Metadefender Core V4.12.2
MetaDefender Core v4.12.2 © 2018 OPSWAT, Inc. All rights reserved. OPSWAT®, MetadefenderTM and the OPSWAT logo are trademarks of OPSWAT, Inc. All other trademarks, trade names, service marks, service names, and images mentioned and/or used herein belong to their respective owners. Table of Contents About This Guide 13 Key Features of Metadefender Core 14 1. Quick Start with Metadefender Core 15 1.1. Installation 15 Operating system invariant initial steps 15 Basic setup 16 1.1.1. Configuration wizard 16 1.2. License Activation 21 1.3. Scan Files with Metadefender Core 21 2. Installing or Upgrading Metadefender Core 22 2.1. Recommended System Requirements 22 System Requirements For Server 22 Browser Requirements for the Metadefender Core Management Console 24 2.2. Installing Metadefender 25 Installation 25 Installation notes 25 2.2.1. Installing Metadefender Core using command line 26 2.2.2. Installing Metadefender Core using the Install Wizard 27 2.3. Upgrading MetaDefender Core 27 Upgrading from MetaDefender Core 3.x 27 Upgrading from MetaDefender Core 4.x 28 2.4. Metadefender Core Licensing 28 2.4.1. Activating Metadefender Licenses 28 2.4.2. Checking Your Metadefender Core License 35 2.5. Performance and Load Estimation 36 What to know before reading the results: Some factors that affect performance 36 How test results are calculated 37 Test Reports 37 Performance Report - Multi-Scanning On Linux 37 Performance Report - Multi-Scanning On Windows 41 2.6. Special installation options 46 Use RAMDISK for the tempdirectory 46 3. Configuring Metadefender Core 50 3.1. Management Console 50 3.2. -

Reduced-Complexity End-To-End Variational Autoencoder for on Board Satellite Image Compression
remote sensing Article Reduced-Complexity End-to-End Variational Autoencoder for on Board Satellite Image Compression Vinicius Alves de Oliveira 1,2,* , Marie Chabert 1 , Thomas Oberlin 3 , Charly Poulliat 1, Mickael Bruno 4, Christophe Latry 4, Mikael Carlavan 5, Simon Henrot 5, Frederic Falzon 5 and Roberto Camarero 6 1 IRIT/INP-ENSEEIHT, University of Toulouse, 31071 Toulouse, France; [email protected] (M.C.); [email protected] (C.P.) 2 Telecommunications for Space and Aeronautics (TéSA) Laboratory, 31500 Toulouse, France 3 ISAE-SUPAERO, University of Toulouse, 31055 Toulouse, France; [email protected] 4 CNES, 31400 Toulouse, France; [email protected] (M.B.); [email protected] (C.L.) 5 Thales Alenia Space, 06150 Cannes, France; [email protected] (M.C.); [email protected] (S.H.); [email protected] (F.F.) 6 ESA, 2201 AZ Noordwijk, The Netherlands; [email protected] * Correspondence: [email protected] Abstract: Recently, convolutional neural networks have been successfully applied to lossy image compression. End-to-end optimized autoencoders, possibly variational, are able to dramatically outperform traditional transform coding schemes in terms of rate-distortion trade-off; however, this is at the cost of a higher computational complexity. An intensive training step on huge databases allows autoencoders to learn jointly the image representation and its probability distribution, pos- sibly using a non-parametric density model or a hyperprior auxiliary autoencoder to eliminate the need for prior knowledge. However, in the context of on board satellite compression, time and memory complexities are submitted to strong constraints. -

Data Compression for Remote Laboratories
Paper—Data Compression for Remote Laboratories Data Compression for Remote Laboratories https://doi.org/10.3991/ijim.v11i4.6743 Olawale B. Akinwale Obafemi Awolowo University, Ile-Ife, Nigeria [email protected] Lawrence O. Kehinde Obafemi Awolowo University, Ile-Ife, Nigeria [email protected] Abstract—Remote laboratories on mobile phones have been around for a few years now. This has greatly improved accessibility of these remote labs to students who cannot afford computers but have mobile phones. When money is a factor however (as is often the case with those who can’t afford a computer), the cost of use of these remote laboratories should be minimized. This work ad- dressed this issue of minimizing the cost of use of the remote lab by making use of data compression for data sent between the user and remote lab. Keywords—Data compression; Lempel-Ziv-Welch; remote laboratory; Web- Sockets 1 Introduction The mobile phone is now the de facto computational device of choice. They are quite powerful, connected devices which are almost always with us. This is so much so that about every important online service has a mobile version or at least a version compatible with mobile phones and tablets (for this paper we would adopt the phrase mobile device to represent mobile phones and tablets). This has caused online labora- tory developers to develop online laboratory solutions which are mobile device- friendly [1, 2, 3, 4, 5, 6, 7, 8]. One of the main benefits of online laboratories is the possibility of using fewer re- sources to serve more people i.e. -

A Novel Coding Architecture for Multi-Line Lidar Point Clouds
This article has been accepted for inclusion in a future issue of this journal. Content is final as presented, with the exception of pagination. IEEE TRANSACTIONS ON INTELLIGENT TRANSPORTATION SYSTEMS 1 A Novel Coding Architecture for Multi-Line LiDAR Point Clouds Based on Clustering and Convolutional LSTM Network Xuebin Sun , Sukai Wang , Graduate Student Member, IEEE, and Ming Liu , Senior Member, IEEE Abstract— Light detection and ranging (LiDAR) plays an preservation of historical relics, 3D sensing for smart city, indispensable role in autonomous driving technologies, such as well as autonomous driving. Especially for autonomous as localization, map building, navigation and object avoidance. driving systems, LiDAR sensors play an indispensable role However, due to the vast amount of data, transmission and storage could become an important bottleneck. In this article, in a large number of key techniques, such as simultaneous we propose a novel compression architecture for multi-line localization and mapping (SLAM) [1], path planning [2], LiDAR point cloud sequences based on clustering and convolu- obstacle avoidance [3], and navigation. A point cloud consists tional long short-term memory (LSTM) networks. LiDAR point of a set of individual 3D points, in accordance with one or clouds are structured, which provides an opportunity to convert more attributes (color, reflectance, surface normal, etc). For the 3D data to 2D array, represented as range images. Thus, we cast the 3D point clouds compression as a range image instance, the Velodyne HDL-64E LiDAR sensor generates a sequence compression problem. Inspired by the high efficiency point cloud of up to 2.2 billion points per second, with a video coding (HEVC) algorithm, we design a novel compression range of up to 120 m. -

In-Place Reconstruction of Delta Compressed Files
In-Place Reconstruction of Delta Compressed Files Randal C. Burns Darrell D. E. Long’ IBM Almaden ResearchCenter Departmentof Computer Science 650 Harry Rd., San Jose,CA 95 120 University of California, SantaCruz, CA 95064 [email protected] [email protected] Abstract results in high latency and low bandwidth to web-enabled clients and prevents the timely delivery of software. We present an algorithm for modifying delta compressed Differential or delta compression [5, 11, compactly en- files so that the compressedversions may be reconstructed coding a new version of a file using only the changedbytes without scratchspace. This allows network clients with lim- from a previous version, can be usedto reducethe size of the ited resources to efficiently update software by retrieving file to be transmitted and consequently the time to perform delta compressedversions over a network. software update. Currently, decompressingdelta encoded Delta compressionfor binary files, compactly encoding a files requires scratch space,additional disk or memory stor- version of data with only the changedbytes from a previous age, used to hold a required second copy of the file. Two version, may be used to efficiently distribute software over copiesof the compressedfile must be concurrently available, low bandwidth channels, such as the Internet. Traditional as the delta file contains directives to read data from the old methods for rebuilding these delta files require memory or file version while the new file version is being materialized storagespace on the target machinefor both the old and new in another region of storage. This presentsa problem. Net- version of the file to be reconstructed. -

Compresso: Efficient Compression of Segmentation Data for Connectomics
Compresso: Efficient Compression of Segmentation Data For Connectomics Brian Matejek, Daniel Haehn, Fritz Lekschas, Michael Mitzenmacher, Hanspeter Pfister Harvard University, Cambridge, MA 02138, USA bmatejek,haehn,lekschas,michaelm,[email protected] Abstract. Recent advances in segmentation methods for connectomics and biomedical imaging produce very large datasets with labels that assign object classes to image pixels. The resulting label volumes are bigger than the raw image data and need compression for efficient stor- age and transfer. General-purpose compression methods are less effective because the label data consists of large low-frequency regions with struc- tured boundaries unlike natural image data. We present Compresso, a new compression scheme for label data that outperforms existing ap- proaches by using a sliding window to exploit redundancy across border regions in 2D and 3D. We compare our method to existing compression schemes and provide a detailed evaluation on eleven biomedical and im- age segmentation datasets. Our method provides a factor of 600-2200x compression for label volumes, with running times suitable for practice. Keywords: compression, encoding, segmentation, connectomics 1 Introduction Connectomics|reconstructing the wiring diagram of a mammalian brain at nanometer resolution|results in datasets at the scale of petabytes [21,8]. Ma- chine learning methods find cell membranes and create cell body labelings for every neuron [18,12,14] (Fig. 1). These segmentations are stored as label volumes that are typically encoded in 32 bits or 64 bits per voxel to support labeling of millions of different nerve cells (neurons). Storing such data is expensive and transferring the data is slow. To cut costs and delays, we need compression methods to reduce data sizes.