Engineering-Based Problem Solving Strategies in AP Calculus
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

APPM 1350 - Calculus 1
APPM 1350 - Calculus 1 Course Objectives: This class will form the basis for many of the standard skills required in all of Engineering, the Sciences, and Mathematics. Specically, students will: • Understand the concepts, techniques and applications of dierential and integral calculus including limits, rate of change of functions, and derivatives and integrals of algebraic and transcendental functions. • Improve problem solving and critical thinking Textbook: Essential Calculus, 2nd Edition by James Stewart. We will cover Chapters 1-5. You will also need an access code for WebAssign’s online homework system. The access code can also be purchased separately. Schedule and Topics Covered Day Section Topics 1 Appendix A Trigonometry 2 1.1 Functions and Their Representation 3 1.2 Essential Functions 4 1.3 The Limit of a Function 5 1.4 Calculating Limits 6 1.5 Continuity 7 1.5/1.6 Continuity/Limits Involving Innity 8 1.6 Limits Involving Innity 9 2.1 Derivatives and Rates of Change 10 Exam 1 Review Exam 1 Topics 11 2.2 The Derivative as a Function 12 2.3 Basic Dierentiation Formulas 13 2.4 Product and Quotient Rules 14 2.5 Chain Rule 15 2.6 Implicit Dierentiation 16 2.7 Related Rates 17 2.8 Linear Approximation and Dierentials 18 3.1 Max and Min Values 19 3.2 The Mean Value Theorem 20 3.3 Derivatives and Shapes of Graphs 21 3.4 Curve Sketching 22 Exam 2 Review Exam 2 Topics 23 3.4/3.5 Curve Sketching/Optimization Problems 24 3.5 Optimization Problems 25 3.6/3.7 Newton’s Method/Antiderivatives 26 3.7/Appendix B Sigma Notation 27 Appendix B, -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

CHAPTER 3: Derivatives
CHAPTER 3: Derivatives 3.1: Derivatives, Tangent Lines, and Rates of Change 3.2: Derivative Functions and Differentiability 3.3: Techniques of Differentiation 3.4: Derivatives of Trigonometric Functions 3.5: Differentials and Linearization of Functions 3.6: Chain Rule 3.7: Implicit Differentiation 3.8: Related Rates • Derivatives represent slopes of tangent lines and rates of change (such as velocity). • In this chapter, we will define derivatives and derivative functions using limits. • We will develop short cut techniques for finding derivatives. • Tangent lines correspond to local linear approximations of functions. • Implicit differentiation is a technique used in applied related rates problems. (Section 3.1: Derivatives, Tangent Lines, and Rates of Change) 3.1.1 SECTION 3.1: DERIVATIVES, TANGENT LINES, AND RATES OF CHANGE LEARNING OBJECTIVES • Relate difference quotients to slopes of secant lines and average rates of change. • Know, understand, and apply the Limit Definition of the Derivative at a Point. • Relate derivatives to slopes of tangent lines and instantaneous rates of change. • Relate opposite reciprocals of derivatives to slopes of normal lines. PART A: SECANT LINES • For now, assume that f is a polynomial function of x. (We will relax this assumption in Part B.) Assume that a is a constant. • Temporarily fix an arbitrary real value of x. (By “arbitrary,” we mean that any real value will do). Later, instead of thinking of x as a fixed (or single) value, we will think of it as a “moving” or “varying” variable that can take on different values. The secant line to the graph of f on the interval []a, x , where a < x , is the line that passes through the points a, fa and x, fx. -

A Gallery of Visualization DEMOS for Related Rate Problems The
A Gallery of Visualization DEMOS for Related Rate Problems The following is a gallery of demos for visualizing common related rate situations. These animations can be used by instructors in a classroom setting or by students to aid in acquiring a visualization background relating to the steps for solving related problems. Two file formats, gif and mov (QuickTime) are available. 1. The gif animations should run on most systems and the file sizes are relatively small. 2. The mov animations require the QuickTime Player which is a free download available by clicking here; these file are also small. (The mov files may not execute properly in old versions of QuickTime.) 3. The collection of animations in gif and mov format can be downloaded; see the 'bulk' zipped download category at the bottom of the following table. General problem Click to view the Animation Sample Click to view the gif file. description. QuickTime file. Click to see gif Click to see mov Filling a conical tank. animation animation Searchlight rotates to Click to see gif Click to see mov follow a walker. animation animation Filling a cylindrical tank, Click to see gif Click to see mov two ways. animation animation Airplane & observer. Click to see gif Click to see mov animation animation Click to see gif Click to see mov Conical sand pile. animation animation Click to see gif Click to see mov Sliding ladder. animation animation Click to see gif Click to see mov Raising ladder. animation animation Shadow of a walking Click to see gif Click to see mov figure. -
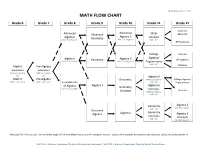
Math Flow Chart
Updated November 12, 2014 MATH FLOW CHART Grade 6 Grade 7 Grade 8 Grade 9 Grade 10 Grade 11 Grade 12 Calculus Advanced Advanced Advanced Math AB or BC Algebra II Algebra I Geometry Analysis MAP GLA-Grade 8 MAP EOC-Algebra I MAP - ACT AP Statistics College Calculus Algebra/ Algebra I Geometry Algebra II AP Statistics MAP GLA-Grade 8 MAP EOC-Algebra I Trigonometry MAP - ACT Math 6 Pre-Algebra Statistics Extension Extension MAP GLA-Grade 6 MAP GLA-Grade 7 or or Algebra II Math 6 Pre-Algebra Geometry MAP EOC-Algebra I College Algebra/ MAP GLA-Grade 6 MAP GLA-Grade 7 MAP - ACT Foundations Trigonometry of Algebra Algebra I Algebra II Geometry MAP GLA-Grade 8 Concepts Statistics Concepts MAP EOC-Algebra I MAP - ACT Geometry Algebra II MAP EOC-Algebra I MAP - ACT Discovery Geometry Algebra Algebra I Algebra II Concepts Concepts MAP - ACT MAP EOC-Algebra I Additional Full Year Courses: General Math, Applied Technical Mathematics, and AP Computer Science. Calculus III is available for students who complete Calculus BC before grade 12. MAP GLA – Missouri Assessment Program Grade Level Assessment; MAP EOC – Missouri Assessment Program End-of-Course Exam Mathematics Objectives Calculus Mathematical Practices 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning. Linear and Nonlinear Functions • Write equations of linear and nonlinear functions in various formats. -

Math 31A Review
Suggestions Differential calculus Integral Calculus Parting thoughts (from Piet Hein) The road to wisdom? Well it’s plain and simple to express: err and err and err again but less and less and less. Problems worthy of attack prove their worth by fighting back. Suggestions Differential calculus Integral Calculus Math 31A Review Steve 12 March 2010 Suggestions Differential calculus Integral Calculus About the final Thursday March 18, 8am-11am, Haines 39 No notes, no book, no calculator Ten questions ≈Four review questions (Chapters 3,4) ≈Five new questions (Chapters 5,6) ≈One essay question No limits, curve sketching, Riemann sums, or density Office hours: Monday 8:30am - 1:30pm Wednesday 10:30am - 3:30pm Suggestions Differential calculus Integral Calculus Start studying well in advance. If you haven’t started yet, start today! The best way to remember anything is through repetition. One of the best ways to help remember things is through regular short review sessions; as compared to one last minute cram session1. Study what ideas and techniques we have gone over this quarter. It is one thing to be able to know an identity or a procedure; it is an entirely different thing to be able to use that identity at the right time and in the right way. 1Also make sure to get plenty of sleep the night before the final. It will help you to focus on the arithmetic and keep you from falling asleep during the final! Suggestions Differential calculus Integral Calculus Learn from your mistakes, otherwise you will repeat them! Look back over your midterms, particularly those where you were not able to complete the problem, and ask “where did I get stuck and how can I avoid getting stuck like that again?” It is helpful to look at the solutions and ask “how would I have thought of that?” or “what about the problem would have told me to do such and such a technique?” Fool me once, shame on you. -

AP Calculus BC Scope & Sequence
AP Calculus BC Scope & Sequence Grading Period Unit Title Learning Targets Throughout the *Apply mathematics to problems in everyday life School Year *Use a problem-solving model that incorporates analyzing information, formulating a plan, determining a solution, justifying the solution and evaluating the reasonableness of the solution *Select tools to solve problems *Communicate mathematical ideas, reasoning and their implications using multiple representations *Create and use representations to organize, record and communicate mathematical ideas *Analyze mathematical relationships to connect and communicate mathematical ideas *Display, explain and justify mathematical ideas and arguments First Grading Preparation for Pre Calculus Review Period Calculus Limits and Their ● An introduction to limits, including an intuitive understanding of the limit process and the Properties formal definition for limits of functions ● Using graphs and tables of data to determine limits of functions and sequences ● Properties of limits ● Algebraic techniques for evaluating limits of functions ● Comparing relative magnitudes of functions and their rates of change (comparing exponential growth, polynomial growth and logarithmic growth) ● Continuity and one-sided limits ● Geometric understanding of the graphs of continuous functions ● Intermediate Value Theorem ● Infinite limits ● Understanding asymptotes in terms of graphical behavior ● Using limits to find the asymptotes of a function, vertical and horizontal Differentiation ● Tangent line to a curve and -

Calculus BC Syllabus
Calculus BC Syllabus Unit Information Unit Name (Timeframe): I. Limits and Continuity (3 weeks) Content and /or Skills Taught: -Intuitive understanding of limits - Using graphs and tables to understand limits - Finding limits analytically - Use limits to justify horizontal and vertical asymptotes - Connect the limits to justify horizontal and vertical asymptotes - Connect the limit as x approaches infinity to global behavior of function - Intuitive understanding of continuity - Definition of continuity - Types of continuity (removable, jump, and infinite) - Prove functions continuous or discontinuous - Intermediate Value Theorem II. Differentiation (3 weeks) Content and /or Skills Taught: - Definition of derivative - Derivative as slope of tangent line - Find derivatives using definition - Use the definition to discover the power rule for finding derivatives - Power rule, sum/difference rule, product rule, quotient rule, chain rule - Location linearization (see curves as locally linear) - Use local linearization to estimate functional values - Derivative as a rate of change - Relationship between differentiability and continuity - Prove functions differentiable or not differentiable - Three cases where the derivative does not exist (discontinuous, vertical tangent, cusp) - Derivatives of the trig functions III. Applications of Derivative (3 weeks) Content and /or Skills Taught: - First derivative test for relative extrema - Justify increasing, decreasing, and relative extrema - justify concavity and inflection points with second derivative -

Unit #5 - Implicit Differentiation, Related Rates
Unit #5 - Implicit Differentiation, Related Rates Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Implicit Differentiation 1. Consider the graph implied by the equation (c) Setting the y value in both equations equal to xy2 = 1. each other and solving to find the intersection point, the only solution is x = 0 and y = 0, so What is the equation of the line through ( 1 ; 2) 4 the two normal lines will intersect at the origin, which is also tangent to the graph? (x; y) = (0; 0). Differentiating both sides with respect to x, Solving process: dy 3 3 y2 + x 2y = 0 (x − 4) + 3 = − (x − 4) − 3 dx 4 4 3 3 so x − 3 + 3 = − x + 3 − 3 4 4 dy −y2 3 3 = x = − x dx 2xy 4 4 6 x = 0 4 dy At the point ( 1 ; 2), = −4, so we can use the x = 0 4 dx point/slope formula to obtain the tangent line y = −4(x − 1=4) + 2 Subbing back into either equation to find y, e.g. y = 3 (0 − 4) + 3 = −3 + 3 = 0. 2. Consider the circle defined by x2 + y2 = 25 4 3. Calculate the derivative of y with respect to x, (a) Find the equations of the tangent lines to given that the circle where x = 4. (b) Find the equations of the normal lines to x4y + 4xy4 = x + y this circle at the same points. (The normal line is perpendicular to the tangent line.) Let x4y + 4xy4 = x + y. Then (c) At what point do the two normal lines in- dy dy dy 4x3y + x4 + (4x) 4y3 + 4y4 = 1 + tersect? dx dx dx hence Differentiating both sides, dy 4yx3 + 4y4 − 1 = : dx 1 − x4 − 16xy3 d d x2 + y2 = (25) dx dx 4. -

A Collection of Problems in Differential Calculus
A Collection of Problems in Differential Calculus Problems Given At the Math 151 - Calculus I and Math 150 - Calculus I With Review Final Examinations Department of Mathematics, Simon Fraser University 2000 - 2010 Veselin Jungic · Petra Menz · Randall Pyke Department Of Mathematics Simon Fraser University c Draft date December 6, 2011 To my sons, my best teachers. - Veselin Jungic Contents Contents i Preface 1 Recommendations for Success in Mathematics 3 1 Limits and Continuity 11 1.1 Introduction . 11 1.2 Limits . 13 1.3 Continuity . 17 1.4 Miscellaneous . 18 2 Differentiation Rules 19 2.1 Introduction . 19 2.2 Derivatives . 20 2.3 Related Rates . 25 2.4 Tangent Lines and Implicit Differentiation . 28 3 Applications of Differentiation 31 3.1 Introduction . 31 3.2 Curve Sketching . 34 3.3 Optimization . 45 3.4 Mean Value Theorem . 50 3.5 Differential, Linear Approximation, Newton's Method . 51 i 3.6 Antiderivatives and Differential Equations . 55 3.7 Exponential Growth and Decay . 58 3.8 Miscellaneous . 61 4 Parametric Equations and Polar Coordinates 65 4.1 Introduction . 65 4.2 Parametric Curves . 67 4.3 Polar Coordinates . 73 4.4 Conic Sections . 77 5 True Or False and Multiple Choice Problems 81 6 Answers, Hints, Solutions 93 6.1 Limits . 93 6.2 Continuity . 96 6.3 Miscellaneous . 98 6.4 Derivatives . 98 6.5 Related Rates . 102 6.6 Tangent Lines and Implicit Differentiation . 105 6.7 Curve Sketching . 107 6.8 Optimization . 117 6.9 Mean Value Theorem . 125 6.10 Differential, Linear Approximation, Newton's Method . 126 6.11 Antiderivatives and Differential Equations . -

Implicit Differentiation and Related Rates
Implicit Differentiation and Related Rates Implicit means “implied or understood though not directly expressed” PART I: Implicit Differentiation The equation has an implicit meaning. It implicitly describes y as a function of x. The equation can be made explicit when we solve it for y so that we have . Here is another “implicit” equation: . This one cannot be made explicit for y in terms of x, even though the values Explicit means “fully revealed, expressed without of y are still dependent upon inputs for x. You cannot solve this vagueness or ambiguity” equation for y. Yet there is still a relationship such that y is a function of x. y still depends on the input for x. And since we are able to define y as a function of x, albeit implicitly, we can still endeavor to find the rate of change of y with respect to x. When we do so, the process is called “implicit differentiation.” Note: All of the “regular” derivative rules apply, with the one special case of using the chain rule whenever the derivative of function of y is taken (see example #2) Example 1 (Real simple one …) Notice that in both examples the a) Find the derivative for the explicit equation . derivative of y is equal to dy/dx. This is a result of the chain rule where we first take the derivative 1 of the general function (y) resulting which just equals 1, followed by the derivative of b) Find the derivative for the implicit equation . the “inside function” y (with respect of x), which is just dy/dx. -

Calculus Overview of the West Virginia College- and Career-Readiness Standards for Mathematics
Calculus Overview of the West Virginia College- and Career-Readiness Standards for Mathematics Included in Policy 2520.2B, the West Virginia College- and Career-Readiness Standards for Mathematics are two types of standards: the Mathematical Habits of Mind and the grade- level Mathematics Content Standards. These standards address the skills, knowledge, and dispositions that students should develop to foster mathematical understanding and expertise, as well as concepts, skills, and knowledge – what students need to understand, know, and be able to do. The standards also require that the Mathematical Habits of Mind and the grade-level Mathematics Content Standards be connected. These connections are essential to support the development of students’ broader mathematical understanding, as students who lack understanding of a topic may rely too heavily on procedures. The Mathematical Habits of Mind must be taught as carefully and practiced as intentionally as the grade-level Mathematics Content Standards are. Neither type should be isolated from the other; mathematics instruction is most effective when these two aspects of the West Virginia College- and Career-Readiness Standards for Mathematics come together as a powerful whole. Mathematical Habits of Mind Overarching Habits of Mind of a Productive Mathematical Thinker MHM1 Make senses of problems and persevere in solving them MHM6 Attend to precision Reasoning Modeling Seeing Structure and Explaining and Using Tools and Generalizing MHM2 MHM4 MHM4 Reason abstracting and Model with mathematics Model with mathematics quantitatively MHM5 MHM5 MHM3 Use appropriate tools Use appropriate tools Construct viable arguments strategically strategically and critique the reasoning of others The eight Mathematical Habits of Mind (MHM) describe the attributes of mathematically proficient students and the expertise that mathematics educators at all levels should seek to develop in their students.