A New Robust Partial Least Squares Re- Gression Method Based on a Robust and an Efficient Adaptive Reweighted Esti- Mator of Covariance
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Curriculum Vitae: Michael W. Trosset
Curriculum Vitae: Michael W. Trosset Department of Statistics Telephone: (812) 856-1178 Indiana University E-mail: [email protected] Bloomington, IN 47401 Web Page: http://www.math.wm.edu/∼trosset/ Education • University of California, Berkeley (Department of Statistics); Fannie & John Hertz Foundation Fellow, September 1978 to December 1981; Dissertation: Minimax Estimation With Side Conditions, directed by Peter J. Bickel; Ph.D., December 1983. • Rice University (Mathematics and Mathematical Sciences); B.A., summa cum laude, May 1978. Employment • Professor, Department of Statistics, Indiana University. August 2006 to present. • Director, Indiana Statistical Consulting Center. August 2006 to present. • Associate Professor, Department of Mathematics, College of William & Mary. August 1998 to June 2006. Promoted to Professor in April 2006. • Formerly Visiting Associate Professor and Adjunct Lecturer, Departments of Mathematics, Statistics, and Psychology, University of Arizona (August 1993 to July 1998); Senior Postdoctoral Fellow, W.M. Keck Center for Computational Biology and Visiting Lecturer, Department of Statistics, Rice Uni- versity (September 1996 to June 1997); Visiting Lecturer, Department of Computational & Applied Mathematics, Rice University (Spring 1993); Consultant (June 1988 to July 1998); Assistant Pro- fessor, Department of Statistics, University of Arizona (August 1984 to December 1988); Instructor, Department of Mathematical Sciences, Rice University (January 1982 to May 1984); Research Assis- tant, Division of -

Newsletter of the Department of Mathematics and Statistics, UMBC
News@Math&Stat Department of Mathematics and Statistics University of Maryland, Baltimore County 1000 Hilltop Circle, Baltimore, MD 21250, 410-455-2412, www.math.umbc.edu Spring 2012, Volume 7, Issue 1, Editor: Angela McNulty ([email protected]) Welcome by Department Chair Nagaraj K. Neerchal It is a pleasure to bring to you the Spring 2012 issue of the department newsletter. The Mathematics and Statistics Department hosted two large conferences; the Infinite Possibilities Conference, which is designed to support minority women in mathematics, and our 6th annual Probability and Statistics Day Conference. Both were a huge success! We’ve also had a number of students recognized throughout the semester at URCAD, the Graduate Research Conference, and Student Recognition Day for their academic and research achievements. Several faculty members have also been recognized this semester for their achievements in teaching and research. I am proud to say that we have a very talented and dedicated group of faculty and students in this department, and it showed this semester! Thank you to everyone who helped to make this spring yet another successful semester for the department. News from the Graduate Program by Program Directors Muruhan Rathinam and Junyong Park Congratulations to the following students who have completed their Master of Science degrees in Applied Mathematics or Statistics in May 2012! In Applied Mathematics: Jesse Haas, Jonathan McHenry*, Jyoti Saraswat*, Serap Tay*, and Ting Wang*. In Statistics: Joshua Betz, Paula Borrego Garza, Sungwoo Choi*, and Merve Gurlu. The students with asterisks beside their names will be continuing their studies in the PhD program. -

Xin-Tu-CV.Pdf
UNIVERSITY OF ROCHESTER Curriculum Vitae December 2013 Xin Ming Tu, Ph.D. Office Address: Department of Biostatistics and Computational Biology University of Rochester 601 Elmwood Ave., Box 630 Rochester, NY 14642 Telephone: (585) 275-0413 (Office) FAX: (585) 573-4865 Email: [email protected] Education: 1982 B.S. Fudan University, Shanghai, People’s Republic of China (Mathematics) 1986 M.A. Duke University, (Statistics and Numerical Analysis) 1989 Ph.D. Duke University, (Statistics and Applied Mathematics) Postgraduate Training and Fellowship Appointments: 1990-1992 Post Doctoral Fellow, Department of Biostatistics, Harvard School of Public Health Military Service: None Faculty Appointments: 1992-1998 Assistant Professor of Statistics and Psychiatry, Department of Statistics and Department of Psychiatry, University of Pittsburgh 1998-1998 Associate Professor of Statistics and Psychiatry, Department of Statistics and Department of Psychiatry, University of Pittsburgh Xin Ming Tu, Ph.D. 2 1998-2003 Associate Professor of Biostatistics, Department of Biostatistics and Epidemiology, University of Pennsylvania, School of Medicine 2003-present Professor of Biostatistics and Psychiatry, Department of Biostatistics and Computational Biology and Department of Psychiatry, University of Rochester School of Medicine 2003-present Director, Statistical Consulting Services (http://www.urmc.rochester.edu/biostat/consulting/) 2007-present Director, Division of Psychiatric Statistics (http://www.urmc.rochester.edu/biostat/dps/) 2007-present Director, -

Area13 ‐ Riviste Di Classe A
Area13 ‐ Riviste di classe A SETTORE CONCORSUALE / TITOLO 13/A1‐A2‐A3‐A4‐A5 ACADEMY OF MANAGEMENT ANNALS ACADEMY OF MANAGEMENT JOURNAL ACADEMY OF MANAGEMENT LEARNING & EDUCATION ACADEMY OF MANAGEMENT PERSPECTIVES ACADEMY OF MANAGEMENT REVIEW ACCOUNTING REVIEW ACCOUNTING, AUDITING & ACCOUNTABILITY JOURNAL ACCOUNTING, ORGANIZATIONS AND SOCIETY ADMINISTRATIVE SCIENCE QUARTERLY ADVANCES IN APPLIED PROBABILITY AGEING AND SOCIETY AMERICAN ECONOMIC JOURNAL. APPLIED ECONOMICS AMERICAN ECONOMIC JOURNAL. ECONOMIC POLICY AMERICAN ECONOMIC JOURNAL: MACROECONOMICS AMERICAN ECONOMIC JOURNAL: MICROECONOMICS AMERICAN JOURNAL OF AGRICULTURAL ECONOMICS AMERICAN POLITICAL SCIENCE REVIEW AMERICAN REVIEW OF PUBLIC ADMINISTRATION ANNALES DE L'INSTITUT HENRI POINCARE‐PROBABILITES ET STATISTIQUES ANNALS OF PROBABILITY ANNALS OF STATISTICS ANNALS OF TOURISM RESEARCH ANNU. REV. FINANC. ECON. APPLIED FINANCIAL ECONOMICS APPLIED PSYCHOLOGICAL MEASUREMENT ASIA PACIFIC JOURNAL OF MANAGEMENT AUDITING BAYESIAN ANALYSIS BERNOULLI BIOMETRICS BIOMETRIKA BIOSTATISTICS BRITISH JOURNAL OF INDUSTRIAL RELATIONS BRITISH JOURNAL OF MANAGEMENT BRITISH JOURNAL OF MATHEMATICAL & STATISTICAL PSYCHOLOGY BROOKINGS PAPERS ON ECONOMIC ACTIVITY BUSINESS ETHICS QUARTERLY BUSINESS HISTORY REVIEW BUSINESS HORIZONS BUSINESS PROCESS MANAGEMENT JOURNAL BUSINESS STRATEGY AND THE ENVIRONMENT CALIFORNIA MANAGEMENT REVIEW CAMBRIDGE JOURNAL OF ECONOMICS CANADIAN JOURNAL OF ECONOMICS CANADIAN JOURNAL OF FOREST RESEARCH CANADIAN JOURNAL OF STATISTICS‐REVUE CANADIENNE DE STATISTIQUE CHAOS CHAOS, SOLITONS -

Rank Full Journal Title Journal Impact Factor 1 Journal of Statistical
Journal Data Filtered By: Selected JCR Year: 2019 Selected Editions: SCIE Selected Categories: 'STATISTICS & PROBABILITY' Selected Category Scheme: WoS Rank Full Journal Title Journal Impact Eigenfactor Total Cites Factor Score Journal of Statistical Software 1 25,372 13.642 0.053040 Annual Review of Statistics and Its Application 2 515 5.095 0.004250 ECONOMETRICA 3 35,846 3.992 0.040750 JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION 4 36,843 3.989 0.032370 JOURNAL OF THE ROYAL STATISTICAL SOCIETY SERIES B-STATISTICAL METHODOLOGY 5 25,492 3.965 0.018040 STATISTICAL SCIENCE 6 6,545 3.583 0.007500 R Journal 7 1,811 3.312 0.007320 FUZZY SETS AND SYSTEMS 8 17,605 3.305 0.008740 BIOSTATISTICS 9 4,048 3.098 0.006780 STATISTICS AND COMPUTING 10 4,519 3.035 0.011050 IEEE-ACM Transactions on Computational Biology and Bioinformatics 11 3,542 3.015 0.006930 JOURNAL OF BUSINESS & ECONOMIC STATISTICS 12 5,921 2.935 0.008680 CHEMOMETRICS AND INTELLIGENT LABORATORY SYSTEMS 13 9,421 2.895 0.007790 MULTIVARIATE BEHAVIORAL RESEARCH 14 7,112 2.750 0.007880 INTERNATIONAL STATISTICAL REVIEW 15 1,807 2.740 0.002560 Bayesian Analysis 16 2,000 2.696 0.006600 ANNALS OF STATISTICS 17 21,466 2.650 0.027080 PROBABILISTIC ENGINEERING MECHANICS 18 2,689 2.411 0.002430 BRITISH JOURNAL OF MATHEMATICAL & STATISTICAL PSYCHOLOGY 19 1,965 2.388 0.003480 ANNALS OF PROBABILITY 20 5,892 2.377 0.017230 STOCHASTIC ENVIRONMENTAL RESEARCH AND RISK ASSESSMENT 21 4,272 2.351 0.006810 JOURNAL OF COMPUTATIONAL AND GRAPHICAL STATISTICS 22 4,369 2.319 0.008900 STATISTICAL METHODS IN -

Ronald Christensen
Ronald Christensen Professor of Statistics University of New Mexico Department of Mathematics and Statistics EDUCATION: Ph.D., Statistics, University of Minnesota, 1983. M.S., Statistics, University of Minnesota, 1976. B.A., Mathematics, University of Minnesota, 1974. EXPERIENCE: 1994- Professor, Department of Mathematics and Statistics, University of New Mexico. 1998-2001, 2003- Founding Director, Statistics Clinic, University of New Mexico. 1988-1994 Associate Professor, Department of Mathematics and Statistics, University of New Mexico. 1982-1988 Assistant Professor, Department of Mathematical Sciences, Montana State Uni- versity. 1994 Visiting Professor, Department of Mathematics and Statistics, University of Canterbury, Chch., N.Z. 1987 Visiting Assistant Professor, Department of Theoretical Statistics, University of Minnesota. RESEARCH INTERESTS: Linear Models Bayesian Inference Log-linear and Logistic Regression Models Statistical Methods SOCIETIES AND HONORS: Fellow of the American Statistical Association, 1996 Fellow of the Institute of Mathematical Statistics, 1998 International Biometric Society American Society for Quality Phi Beta Kappa 1 PUBLICATIONS: 1. Christensen, Ronald (2007). \Notes on the decompostion of effects in full factorial experimental designs." Quality Engineering, accepted. (Letter.) 2. Yang, Mingan, Hanson, Timothy, and Christensen, Ronald (2007). \Nonparametric Bayesian estimation of a bivariate density with interval censored data." Statistics in Medicine, under review. 3. Christensen, Ronald (2007). \Discussion: Dimension reduction, nonparametric regres- sion, and multivariate linear models." Statistical Science, accepted. 4. Christensen, Ronald and Johnson, Wesley (2007). \A Conversation with Seymour Geisser." Statistical Science, accepted. 5. Christensen, Ronald (2006). \Comment on Monahan (2006)." The American Statisti- cian, 60, 295. 6. Christensen, Ronald (2006). \General prediction theory and the role of R2." The American Statistician, under revision. -

2018 Journal Citation Reports Journals in the 2018 Release of JCR 2 Journals in the 2018 Release of JCR
2018 Journal Citation Reports Journals in the 2018 release of JCR 2 Journals in the 2018 release of JCR Abbreviated Title Full Title Country/Region SCIE SSCI 2D MATER 2D MATERIALS England ✓ 3 BIOTECH 3 BIOTECH Germany ✓ 3D PRINT ADDIT MANUF 3D PRINTING AND ADDITIVE MANUFACTURING United States ✓ 4OR-A QUARTERLY JOURNAL OF 4OR-Q J OPER RES OPERATIONS RESEARCH Germany ✓ AAPG BULL AAPG BULLETIN United States ✓ AAPS J AAPS JOURNAL United States ✓ AAPS PHARMSCITECH AAPS PHARMSCITECH United States ✓ AATCC J RES AATCC JOURNAL OF RESEARCH United States ✓ AATCC REV AATCC REVIEW United States ✓ ABACUS-A JOURNAL OF ACCOUNTING ABACUS FINANCE AND BUSINESS STUDIES Australia ✓ ABDOM IMAGING ABDOMINAL IMAGING United States ✓ ABDOM RADIOL ABDOMINAL RADIOLOGY United States ✓ ABHANDLUNGEN AUS DEM MATHEMATISCHEN ABH MATH SEM HAMBURG SEMINAR DER UNIVERSITAT HAMBURG Germany ✓ ACADEMIA-REVISTA LATINOAMERICANA ACAD-REV LATINOAM AD DE ADMINISTRACION Colombia ✓ ACAD EMERG MED ACADEMIC EMERGENCY MEDICINE United States ✓ ACAD MED ACADEMIC MEDICINE United States ✓ ACAD PEDIATR ACADEMIC PEDIATRICS United States ✓ ACAD PSYCHIATR ACADEMIC PSYCHIATRY United States ✓ ACAD RADIOL ACADEMIC RADIOLOGY United States ✓ ACAD MANAG ANN ACADEMY OF MANAGEMENT ANNALS United States ✓ ACAD MANAGE J ACADEMY OF MANAGEMENT JOURNAL United States ✓ ACAD MANAG LEARN EDU ACADEMY OF MANAGEMENT LEARNING & EDUCATION United States ✓ ACAD MANAGE PERSPECT ACADEMY OF MANAGEMENT PERSPECTIVES United States ✓ ACAD MANAGE REV ACADEMY OF MANAGEMENT REVIEW United States ✓ ACAROLOGIA ACAROLOGIA France ✓ -

Allegato 1 MC(1)
ALLEGATO 1 - ELENCO DELLE RIVISTE DA ESPUNGERE RIVISTA JR EcLit SIE ASIA PACIFIC JOURNAL OF MANAGEMENT D NP BUSINESS ETHICS QUARTERLY D NP BUSINESS HORIZONS D NP COMPUTATIONAL OPTIMIZATION AND APPLICATIONS D NP CORPORATE GOVERNANCE: AN INTERNATIONAL REVIEW D NP EUROPEAN JOURNAL OF WORK AND ORGANIZATIONAL PSYCHOLOGY D NP INTERNATIONAL JOURNAL OF INFORMATION TECHNOLOGY & DECISION MAKING D NP INZINERINE EKONOMIKA - Engineering Economic D NP JOURNAL OF BUSINESS RESEARCH D NP JOURNAL OF MANAGEMENT DEVELOPMENT D NP JOURNAL OF MANAGERIAL PSYCHOLOGY D NP JOURNAL OF MULTIVARIATE ANALYSIS D NP JOURNAL OF NURSING MANAGEMENT D NP JOURNAL OF PUBLIC POLICY & MARKETING D NP JOURNAL OF SERVICE RESEARCH D NP JOURNAL OF SERVICES MARKETING D NP JOURNAL OF THE OPERATIONAL RESEARCH SOCIETY D NP NONLINEAR ANALYSIS: Real World Applications D NP SOCIAL POLICY & ADMINISTRATION D NP NAVAL RESEARCH LOGISTIC E NP ACADEMY OF MANAGEMENT LEARNING & EDUCATION NP NP ACADEMY OF MANAGEMENT PERSPECTIVES NP NP ACCOUNTING, AUDITING & ACCOUNTABILITY JOURNAL NP NP ACCOUNTING, ORGANIZATIONS AND SOCIETY NP NP ADVANCES IN APPLIED PROBABILITY NP NP AGEING AND SOCIETY NP NP AMERICAN REVIEW OF PUBLIC ADMINISTRATION NP NP ANNALES DE L'INSTITUT HENRI POINCARE-PROBABILITES ET STATISTIQUES NP NP ANNALS OF APPLIED PROBABILITY NP NP ANNALS OF APPLIED STATISTICS NP NP ANNALS OF PROBABILITY NP NP ANNALS OF STATISTICS NP NP APPLIED PSYCHOLOGICAL MEASUREMENT NP NP AUDITING NP NP BAYESIAN ANALYSIS NP NP BERNOULLI NP NP BIOMETRICS NP NP BIOMETRIKA NP NP BIOSTATISTICS NP NP BRITISH JOURNAL OF -

Listado De Revistas 2018 Revista Nombre Completo Clasificacion 1 Abstr
LISTADO DE REVISTAS 2018 REVISTA NOMBRE COMPLETO CLASIFICACION 1 ABSTR. APPL. ANAL. ABSTRACT AND APPLIED ANALYSIS R 2 ACTA APPL. MATH. ACTA APPLICANDAE MATHEMATICAE B 3 ACTA ARITH. ACTA ARITHMETICA B 4 ACTA MATH. ACTA MATHEMATICA MB 5 ACTA MATH. HUNGAR. ACTA MATHEMATICA HUNGARICA R 6 ACTA MATH. SCI. SER. B ENGL. ED. ACTA MATHEMATICA SCIENTIA. SERIES B. ENGLISH EDITION R 7 ACTA MATH. SIN. (ENGL. SER.) ACTA MATHEMATICA SINICA (ENGLISH SERIES) R 8 ACTA NUMER. ACTA NUMERICA MB 9 ADV. MODEL. OPTIM. ADVANCED MODELING AND OPTIMIZATION R 10 ADV. NONLINEAR STUD. ADVANCED NONLINEAR STUDIES B 11 ADV. APPL. CLIFFORD ALGEBR. ADVANCES IN APPLIED CLIFFORD ALGEBRAS R 12 ADV. IN APPL. MATH. ADVANCES IN APPLIED MATHEMATICS B 13 AAMM ADVANCES IN APPLIED MATHEMATICS AND MECHANICS R 14 ADV. IN APPL. PROBAB. ADVANCES IN APPLIED PROBABILITY B 15 ADV. IN CALCULUS OF VARIATIONS ADVANCES IN CALCULUS OF VARIATIONS B 16 ADV COMPUT MATH ADVANCES IN COMPUTATIONAL MATHEMATICS B 17 ADV. DIFFERENCE EQU. ADVANCES IN DIFFERENCE EQUATIONS R 18 ADV. DIFFERENTIAL EQUATIONS ADVANCES IN DIFFERENTIAL EQUATIONS B 19 ADV. GEOM. ADVANCES IN GEOMETRY B 20 ADV. MATH. SCI. APPL. ADVANCES IN MATHEMATICAL SCIENCES AND APPLICATIONS R 21 ADV. MATH. ADVANCES IN MATHEMATICS MB 22 ADVANCES IN PURE MATHEMATICS ADVANCES IN PURE MATHEMATICS R 23 AEQUATIONES MATH. AEQUATIONES MATHEMATICAE R ALEA LAT. AM. J. PROBAB. MATH. 24 ALEA. LATIN AMERICAN JOURNAL OF PROBABILITY AND MATHEMATICAL STATISTICS B STAT. 25 ALGEBR NUMBER THEORY ALGEBRA AND NUMBER THEORY MB 26 ALGEBRA COLLOQ. ALGEBRA COLLOQUIUM B 27 ALGEBRA UNIVERSALIS ALGEBRA UNIVERSALIS B 28 ALGEBR. GEOM. TOPOL. -

TITLE TITLE20 COUNTRY SCIENCE SOCIAL SCIENCE Journal Of
2016 SOCIAL TITLE TITLE20 COUNTRY SCIENCE SCIENCE Journal of Breast Cancer J BREAST CANCER SOUTH KOREA TRUE FALSE Journal of Breath Research J BREATH RES ENGLAND TRUE FALSE Journal of Bridge Engineering J BRIDGE ENG UNITED STATES TRUE FALSE JOURNAL OF BRITISH STUD- J BRIT STUD UNITED STATES FALSE TRUE IES JOURNAL OF BROADCASTING J BROADCAST ELEC- UNITED STATES FALSE TRUE & ELECTRONIC MEDIA TRON JOURNAL OF BRYOLOGY J BRYOL ENGLAND TRUE FALSE Journal of Building Performance J BUILD PERFORM ENGLAND TRUE FALSE Simulation SIMU Journal of Building Physics J BUILD PHYS ENGLAND TRUE FALSE Journal of BUON J BUON GREECE TRUE FALSE Journal of Burn Care & Re- J BURN CARE RES UNITED STATES TRUE FALSE search JOURNAL OF BUSINESS & J BUS ECON STAT UNITED STATES TRUE TRUE ECONOMIC STATISTICS JOURNAL OF BUSINESS & J BUS IND MARK UNITED STATES FALSE TRUE INDUSTRIAL MARKETING JOURNAL OF BUSINESS AND J BUS PSYCHOL UNITED STATES FALSE TRUE PSYCHOLOGY JOURNAL OF BUSINESS AND J BUS TECH COMMUN UNITED STATES FALSE TRUE TECHNICAL COMMUNICATION Journal of Business Economics J BUS ECON MANAG LITHUANIA FALSE TRUE and Management JOURNAL OF BUSINESS ETH- J BUS ETHICS NETHERLANDS FALSE TRUE ICS Journal of Business Finance & J BUS FINAN ACCOUNT ENGLAND FALSE TRUE Accounting Journal of Business Logistics J BUS LOGIST UNITED STATES FALSE TRUE JOURNAL OF BUSINESS RE- J BUS RES UNITED STATES FALSE TRUE SEARCH JOURNAL OF BUSINESS VEN- J BUS VENTURING UNITED STATES FALSE TRUE TURING Journal of Business-to-Business J BUS-BUS MARK UNITED STATES FALSE TRUE Marketing Journal of -
Statistics Promotion and Tenure Guidelines
Approved by Department 12/05/2013 Approved by Faculty Relations May 20, 2014 UFF Notified May 21, 2014 Effective Spring 2016 2016-17 Promotion Cycle Department of Statistics Promotion and Tenure Guidelines The purpose of these guidelines is to give explicit definitions of what constitutes excellence in teaching, research and service for tenure-earning and tenured faculty. Research: The most common outlet for scholarly research in statistics is in journal articles appearing in refereed publications. Based on the five-year Impact Factor (IF) from the ISI Web of Knowledge Journal Citation Reports, the top 50 journals in Probability and Statistics are: 1. Journal of Statistical Software 26. Journal of Computational Biology 2. Econometrica 27. Annals of Probability 3. Journal of the Royal Statistical Society 28. Statistical Applications in Genetics and Series B – Statistical Methodology Molecular Biology 4. Annals of Statistics 29. Biometrical Journal 5. Statistical Science 30. Journal of Computational and Graphical Statistics 6. Stata Journal 31. Journal of Quality Technology 7. Biostatistics 32. Finance and Stochastics 8. Multivariate Behavioral Research 33. Probability Theory and Related Fields 9. Statistical Methods in Medical Research 34. British Journal of Mathematical & Statistical Psychology 10. Journal of the American Statistical 35. Econometric Theory Association 11. Annals of Applied Statistics 36. Environmental and Ecological Statistics 12. Statistics in Medicine 37. Journal of the Royal Statistical Society Series C – Applied Statistics 13. Statistics and Computing 38. Annals of Applied Probability 14. Biometrika 39. Computational Statistics & Data Analysis 15. Chemometrics and Intelligent Laboratory 40. Probabilistic Engineering Mechanics Systems 16. Journal of Business & Economic Statistics 41. Statistica Sinica 17. -
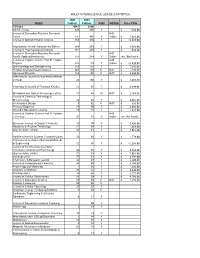
Wiley Interscience Usage Statistics
WILEY INTERSCIENCE USAGE STATISTICS 2006 2007 WILEY Fulltext Fulltext NJKI NOTES Price FY08 TOTALS 4647 5166 AIChE Journal 426 496 Y $ 1,789.00 Journal of Biomedical Materials Research A+B Part A 191 482 Y Online $ 7,982.00 Journal of Applied Polymer Science 759 470 Y $ 19,935.00 Angewandte Chemie International Edition 164 264 Y $ 6,568.00 Journal of Pharmaceutical Sciences 161 239 Y $ 1,539.00 Journal of Biomedical Materials Research A+B Part B: Applied Biomaterials 113 214 Y Online see JBM Part A Journal of Polymer Science Part B: Polymer A+B Physics 323 179 Y Online $ 15,820.00 Biotechnology and Bioengineering 112 136 Y $ 7,345.00 Polymer Engineering and Science 467 129 N NJIT $ 1,273.00 Advanced Materials 188 126 N NJIT $ 4,990.00 International Journal for Numerical Methods in Fluids 22 102 Y $ 5,655.00 International Journal of Chemical Kinetics 37 97 Y $ 4,099.00 Microwave and Optical Technology Letters 17 84 N NJIT $ 2,764.00 Journal of Chemical Technology & Biotechnology 49 82 Y $ 2,205.00 Architectural Design 0 82 N NJIT $ 335.00 Prenatal Diagnosis 18 80 Y $ 2,662.00 Strategic Management Journal 18 72 Y $ 1,917.00 Journal of Polymer Science Part A: Polymer A+B Chemistry 97 71 Y Online see JPS Part B European Journal of Organic Chemistry 15 70 Y $ 5,896.00 Advances in Polymer Technology 47 64 Y $ 1,358.00 physica status solidi b 35 61 Y $ 7,063.00 Particle & Particle Systems Characterization 26 60 Y $ 1,779.00 International Journal for Numerical Methods in Engineering 12 56 Y $ 11,259.00 Journal of the American Society for Information