DOCSLIB.ORG

A Dynamic Survey of Graph Labeling

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Dynamic Survey of Graph Labeling A Dynamic Survey of Graph Labeling Joseph A. Gallian Department of Mathematics and Statistics University of Minnesota Duluth Duluth, Minnesota 55812 [email protected] Submitted: September 1, 1996; Accepted: November 14, 1997 Fifteenth edition, December 7, 2012 Mathematics Subject Classifications: 05C78 Abstract A graph labeling is an assignment of integers to the vertices or edges, or both, subject to certain conditions. Graph labelings were first introduced in the late 1960s. In the intervening years dozens of graph labelings techniques have been studied in over 1500 papers. Finding out what has been done for any particular kind of labeling and keeping up with new discoveries is difficult because of the sheer number of papers and because many of the papers have appeared in journals that are not widely available. In this survey I have collected everything I could find on graph labeling. For the convenience of the reader the survey includes a detailed table of contents and index. the electronic journal of combinatorics 16 (2010), #DS6 1 Contents 1 Introduction 5 2 Graceful and Harmonious Labelings 7 2.1 Trees . 7 2.2 Cycle-Related Graphs . 9 2.3 Product Related Graphs . 14 2.4 Complete Graphs . 16 2.5 Disconnected Graphs . 18 2.6 Joins of Graphs . 20 2.7 Miscellaneous Results . 21 2.8 Summary . 24 Table 1: Summary of Graceful Results . 26 Table 2: Summary of Harmonious Results . 30 3 Variations of Graceful Labelings 33 3.1 α-labelings . 33 Table 3: Summary of Results on α-labelings . 39 3.2 k-graceful Labelings . 40 3.3 γ-Labelings . 42 3.4 Skolem-Graceful Labelings . 42 3.5 Odd-Graceful Labelings . 44 3.6 Graceful-like Labelings . 46 3.7 Cordial Labelings . 51 3.8 The Friendly Index{Balance Index . 59 3.9 Hamming-graceful Labelings . 65 4 Variations of Harmonious Labelings 65 4.1 Sequential and Strongly c-harmonious Labelings . 65 4.2 (k; d)-arithmetic Labelings . 68 4.3 (k; d)-indexable Labelings . 69 4.4 Elegant Labelings . 71 4.5 Felicitous Labelings . 72 4.6 Odd Harmonious and Even Harmonious Labelings . 74 5 Magic-type Labelings 75 5.1 Magic Labelings . 75 Table 4: Summary of Magic Labelings . 80 5.2 Edge-magic Total and Super Edge-magic Total Labelings . 82 Table 5: Summary of Edge-magic Total Labelings . 94 Table 6: Summary of Super Edge-magic Labelings . 97 5.3 Vertex-magic Total Labelings . 101 Table 7: Summary of Vertex-magic Total Labelings . 107 Table 8: Summary of Super Vertex-magic Total Labelings . 109 Table 9: Summary of Totally Magic Labelings . 109 5.4 Magic Labelings of Type (a; b; c) ...........................110 the electronic journal of combinatorics 16 (2010), #DS6 2 Table 10: Summary of Magic Labelings of Type (a; b; c) . 111 5.5 Sigma Labelings/1-vertex magic labelings . 112 5.6 Other Types of Magic Labelings . 112 6 Antimagic-type Labelings 119 6.1 Antimagic Labelings . 119 Table 11: Summary of Antimagic Labelings . 124 Table 12: Summary of (a; d)-Edge-Antimagic Vertex Labelings . 125 Table 13: Summary of (a; d)-Antimagic Labelings . 126 6.2 (a; d)-Antimagic Total Labelings . 127 Table 14: Summary of (a; d)-Vertex-Antimagic Total and Super (a; d)-Vertex- Antimagic Total Labelings . 135 Table 15: Summary of (a; d)-Edge-Antimagic Total Labelings . 136 Table 16: Summary of (a; d)-Super-Edge-Antimagic Total Labelings . 138 6.3 Face Antimagic Labelings and d-antimagic Labeling of Type (1,1,1) . 139 Table 17: Summary of Face Antimagic Labelings . 141 Table 18: Summary of d-antimagic Labelings of Type (1,1,1) . 142 6.4 Product Antimagic Labelings . 143 7 Miscellaneous Labelings 144 7.1 Sum Graphs . 144 Table 19: Summary of Sum Graph Labelings . 150 7.2 Prime and Vertex Prime Labelings . 151 Table 20: Summary of Prime Labelings . 155 Table 21: Summary of Vertex Prime Labelings . 158 7.3 Edge-graceful Labelings . 159 Table 22: Summary of Edge-graceful Labelings . 166 7.4 Radio Labelings . 167 7.5 Line-graceful Labelings . 168 7.6 Representations of Graphs modulo n . 169 7.7 k-sequential Labelings . 170 7.8 IC-colorings . 170 7.9 Product Cordial Labelings . 171 7.10 Prime Cordial Labelings . 174 7.11 Geometric Labelings . 175 7.12 Strongly Multiplicative Graphs . 176 7.13 Mean Labelings . 177 7.14 Irregular Total Labelings . 180 7.15 Minimal k-rankings . 182 7.16 Set Graceful and Set Sequential Graphs . 183 7.17 Vertex Equitable Graphs . 184 7.18 Sequentially Additive Graphs . 184 7.19 Difference Graphs . 185 7.20 Square Sum Labelings . 185 7.21 Permutation and Combination Graphs . 185 7.22 Strongly *-graphs . 186 the electronic journal of combinatorics 16 (2010), #DS6 3 7.23 Triangular Sum Graphs . 186 7.24 Divisor Graphs . 186 References 186 Index 268 the electronic journal of combinatorics 16 (2010), #DS6 4 1 Introduction Most graph labeling methods trace their origin to one introduced by Rosa [1033] in 1967, or one given by Graham and Sloane [503] in 1980. Rosa [1033] called a function f a β-valuation of a graph G with q edges if f is an injection from the vertices of G to the set f0; 1; : : : ; qg such that, when each edge xy is assigned the label jf(x) − f(y)j, the resulting edge labels are distinct. Golomb [494] subsequently called such labelings graceful and this is now the popular term. Rosa introduced β-valuations as well as a number of other labelings as tools for decomposing the complete graph into isomorphic subgraphs. In particular, β-valuations originated as a means of attacking the conjecture of Ringel [1022] that K2n+1 can be decomposed into 2n + 1 subgraphs that are all isomorphic to a given tree with n edges. Although an unpublished result of Erd}os says that most graphs are not graceful (see [503]), most graphs that have some sort of regularity of structure are graceful. Sheppard [1130] has shown that there are exactly q! gracefully labeled graphs with q edges. Rosa [1033] has identified essentially three reasons why a graph fails to be graceful: (1) G has \too many vertices" and \not enough edges," (2) G \has too many edges," and (3) G \has the wrong parity." The disjoint union of trees is a case where there are too many vertices for the number of edges. An infinite class of graphs that are not graceful for the second reason is given in [236]. As an example of the third condition Rosa [1033] has shown that if every vertex has even degree and the number of edges is congruent to 1 or 2 (mod 4) then the graph is not graceful. In particular, the cycles C4n+1 and C4n+2 are not graceful. Acharya [12] proved that every graph can be embedded as an induced subgraph of a graceful graph and a connected graph can be embedded as an induced subgraph of a graceful connected graph. Acharya, Rao, and Arumugam [30] proved: every triangle-free graph can be embedded as an induced subgraph of a triangle-free graceful graph; every planar graph can be embedded as an induced subgraph of a planar graceful graph; and every tree can be embedded as an induced subgraph of a graceful tree. These results demonstrate that there is no forbidden subgraph characterization of these particular kinds of graceful graphs. Harmonious graphs naturally arose in the study by Graham and Sloane [503] of modular versions of additive bases problems stemming from error-correcting codes. They defined a graph G with q edges to be harmonious if there is an injection f from the vertices of G to the group of integers modulo q such that when each edge xy is assigned the label f(x) + f(y) (mod q), the resulting edge labels are distinct. When G is a tree, exactly one label may be used on two vertices. They proved that almost all graphs are not harmonious. Analogous to the \parity" necessity condition for graceful graphs, Graham and Sloane proved that if a harmonious graph has an even number of edges q and the degree of every vertex is divisible by 2k then q is divisible by 2k+1. Thus, for example, a book with seven pages (i.e., the cartesian product of the complete bipartite graph K1;7 and a path of length 1) is not harmonious. Liu and Zhang [854] have generalized this condition as follows: if a harmonious graph with q edges has degree sequence d1; d2; : : : ; dp then gcd(d1; d2; : : : dp; q) divides q(q−1)=2. They have also proved that every graph is a subgraph of a harmonious graph. More generally, Sethuraman and Elumalai [1100] have shown that any given set of graphs G1;G2;:::;Gt can be embedded in a graceful or harmonious graph. Determining whether a graph has a harmonious labeling was shown to be NP-complete by Auparajita, Dulawat, and Rathore in 2001 (see [715]). In the early 1980s Bloom and Hsu [245], [246],[230] extended graceful labelings to directed graphs by defining a graceful labeling on a directed graph D(V; E) as a one-to-one map θ from V to f0; 1; 2;:::; jEjg such that θ(y) − θ(x) mod (jEj + 1) is distinct for every edge xy in E. the electronic journal of combinatorics 16 (2010), #DS6 5 Graceful labelings of directed graphs also arose in the characterization of finite neofields by.
Load more

Recommended publications
  • COMPUTING the TOPOLOGICAL INDICES for CERTAIN FAMILIES of GRAPHS 1Saba Sultan, 2Wajeb Gharibi, 2Ali Ahmad 1Abdus Salam School of Mathematical Sciences, Govt
    Sci.Int.(Lahore),27(6),4957-4961,2015 ISSN 1013-5316; CODEN: SINTE 8 4957 COMPUTING THE TOPOLOGICAL INDICES FOR CERTAIN FAMILIES OF GRAPHS 1Saba Sultan, 2Wajeb Gharibi, 2Ali Ahmad 1Abdus Salam School of Mathematical Sciences, Govt. College University, Lahore, Pakistan. 2College of Computer Science & Information Systems, Jazan University, Jazan, KSA. [email protected], [email protected], [email protected] ABSTRACT. There are certain types of topological indices such as degree based topological indices, distance based topological indices and counting related topological indices etc. Among degree based topological indices, the so-called atom-bond connectivity (ABC), geometric arithmetic (GA) are of vital importance. These topological indices correlate certain physico-chemical properties such as boiling point, stability and strain energy etc. of chemical compounds. In this paper, we compute formulas of General Randi´c index ( ) for different values of α , First zagreb index, atom-bond connectivity (ABC) index, geometric arithmetic GA index, the fourth ABC index ( ABC4 ) , fifth GA index ( GA5 ) for certain families of graphs. Key words: Atom-bond connectivity (ABC) index, Geometric-arithmetic (GA) index, ABC4 index, GA5 index. 1. INTRODUCTION AND PRELIMINARY RESULTS Cheminformatics is a new subject which relates chemistry, is connected graph with vertex set V(G) and edge set E(G), du mathematics and information science in a significant manner. The is the degree of vertex and primary application of cheminformatics is the storage, indexing and search of information relating to compounds. Graph theory has provided a vital role in the aspect of indexing. The study of ∑ Quantitative structure-activity (QSAR) models predict biological activity using as input different types of structural parameters of where .
    [Show full text]
  • Some Families of Convex Polytopes Labeled by 3-Total Edge Product Cordial Labeling
    Punjab University Journal of Mathematics (ISSN 1016-2526) Vol. 49(3)(2017) pp. 119-132 Some Families of Convex Polytopes Labeled by 3-Total Edge Product Cordial Labeling Umer Ali Department of Mathematics, UMT Lahore, Pakistan. Email: [email protected] Muhammad bilal Department of Mathematics, UMT Lahore, Pakistan. Email: [email protected] Sohail Zafar Department of Mathematics, UMT Lahore, Pakistan. Email: [email protected] Zohaib Zahid Department of Mathematics, UMT Lahore, Pakistan. Email: zohaib [email protected] Received: 03 January, 2017 / Accepted: 10 April, 2017 / Published online: 18 August, 2017 Abstract. For a graph G = (VG;EG), consider a mapping h : EG ! ∗ f0; 1; 2; : : : ; k − 1g, 2 ≤ k ≤ jEGj which induces a mapping h : VG ! ∗ Qn f0; 1; 2; : : : ; k − 1g such that h (v) = i=1 h(ei)( mod k), where ei is an edge incident to v. Then h is called k-total edge product cordial ( k- TEPC) labeling of G if js(i) − s(j)j ≤ 1 for all i; j 2 f1; 2; : : : ; k − 1g: Here s(i) is the sum of all vertices and edges labeled by i. In this paper, we study k-TEPC labeling for some families of convex polytopes for k = 3. AMS (MOS) Subject Classification Codes: 05C07 Key Words: 3-TEPC labeling, The graphs of convex polytopes. 119 120 Umer Ali, Muhammad Bilal, Sohail Zafar and Zohaib Zahid 1. INTRODUCTION AND PRELIMINARIES Let G be an undirected, simple and finite graph with vertex-set VG and edge-set EG. Order of a graph G is the number of vertices and size of a graph G is the number of edges.
    [Show full text]
  • Odd Harmonious Labeling on Pleated of the Dutch Windmill Graphs
    CAUCHY – JURNAL MATEMATIKA MURNI DAN APLIKASI Volume 4 (4) (2017), Pages 161-166 p-ISSN: 2086-0382; e-ISSN: 2477-3344 Odd Harmonious Labeling on Pleated of the Dutch Windmill Graphs Fery Firmansah1, Muhammad Ridlo Yuwono2 1, 2Mathematics Edu. Depart. University of Widya Dharma Klaten, Indonesia Email: [email protected], [email protected] ABSTRACT A graph 퐺(푉(퐺), 퐸(퐺)) is called graph 퐺(푝, 푞) if it has 푝 = |푉(퐺)| vertices and 푞 = |퐸(퐺)| edges. The graph 퐺(푝, 푞) is said to be odd harmonious if there exist an injection 푓: 푉(퐺) → {0,1,2, … ,2푞 − 1} such that the induced function 푓∗: 퐸(퐺) → {1,3,5, … ,2푞 − 1} defined by 푓∗(푢푣) = 푓(푢) + 푓(푣). The function 푓∗ is a bijection and 푓 is said to be odd harmonious labeling of 퐺(푝, 푞). In this paper we prove that pleated of the (푘) Dutch windmill graphs 퐶4 (푟) with 푘 ≥ 1 and 푟 ≥ 1 are odd harmonious graph. Moreover, we also give odd (푘) (푘) harmonious labeling construction for the union pleated of the Dutch windmill graph 퐶4 (푟) ∪ 퐶4 (푟) with 푘 ≥ 1 and 푟 ≥ 1. Keywords: odd harmonious labeling, pleated graph, the Dutch windmill graph INTRODUCTION In this paper we consider simple, finite, connected and undirected graph. A graph 퐺(푝, 푞) with 푝 = |푉(퐺)| vertices and 푞 = |퐸(퐺)| edges. A graph labeling which has often been motivated by practical problems is one of fascinating areas of research. Labeled graphs serves as useful mathematical models for many applications in coding theory, communication networks, and mobile telecommunication system.
    [Show full text]
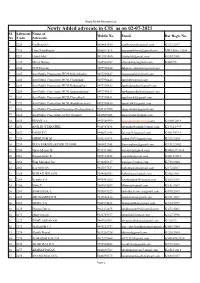
  • Newly Added Advocate in CIS As on 02-07-2021 Sl Advocate Name of Mobile No
    Newly Added Advocate List Newly Added advocate in CIS as on 02-07-2021 Sl Advocate Name of Mobile No. Email Bar Regn. No. No Code Advocate 1 2225 Pradheep K U 9656653590 [email protected] K/333/2017 2 2226 Lijan Panjikkaran 8606511519 [email protected] MH/1405-c /2004 3 2227 Lloyd Arby 9611951080 [email protected] K/539/2016 4 2228 Oliver Dantes 9388530767 [email protected] K/608/98 5 2246 DDP,Thrissur 9497990424 [email protected] 6 2247 Asst Public Prosecutor(JFCM,Irinjalakuda)) 9497990427 [email protected] 7 2248 Asst Public Prosecutor(JFCM,Chalakudy) 9497990428 [email protected] 8 2249 Asst Public Prosecutor(JFCM,Kodungallur) 9497990432 [email protected] 9 2250 Asst Public Prosecutor(JFCM,Kunnamkulam) 9497990429 [email protected] 10 2251 Asst Public Prosecutor(JFCM,Chavakkad) 9797990431 [email protected] 11 2252 Asst Public Prosecutor(JFCM,Wadakkanchery) 9497990430 [email protected] 12 2253 Asst Public Prosecutor(Nyayalaya,Pazhayannur)) 9947337090 [email protected] 13 2254 Asst Public Prosecutor(ACJM,Thrissur) 8547829086 [email protected] 14 2255 SUNNY A L 9995509999 [email protected] K/1069/2019 15 2256 ANIL KOTTARATHIL 9946947496 [email protected] K/1914/1999 16 2257 DAVIS T.G 9446872146 [email protected] K/001347/19 17 2258 MIDHUN M M 9656118195 [email protected] K/429/2020 18 2259 DIXO VARGHESE PORUTHOOR 9880031346 [email protected] K/1512/2002 19 2260 Surya Menon. K 8943733002 [email protected] K/000139/2018 20 2261 Rajasekharan K 9496125452
    [Show full text]
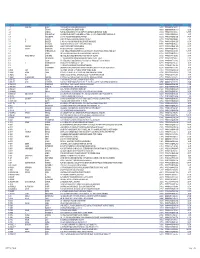
  • SR NO First Name Middle Name Last Name Address Pincode Folio
    SR NO First Name Middle Name Last Name Address Pincode Folio Amount 1 A SPRAKASH REDDY 25 A D REGIMENT C/O 56 APO AMBALA CANTT 133001 0000IN30047642435822 22.50 2 A THYAGRAJ 19 JAYA CHEDANAGAR CHEMBUR MUMBAI 400089 0000000000VQA0017773 135.00 3 A SRINIVAS FLAT NO 305 BUILDING NO 30 VSNL STAFF QTRS OSHIWARA JOGESHWARI MUMBAI 400102 0000IN30047641828243 1,800.00 4 A PURUSHOTHAM C/O SREE KRISHNA MURTY & SON MEDICAL STORES 9 10 32 D S TEMPLE STREET WARANGAL AP 506002 0000IN30102220028476 90.00 5 A VASUNDHARA 29-19-70 II FLR DORNAKAL ROAD VIJAYAWADA 520002 0000000000VQA0034395 405.00 6 A H SRINIVAS H NO 2-220, NEAR S B H, MADHURANAGAR, KAKINADA, 533004 0000IN30226910944446 112.50 7 A R BASHEER D. NO. 10-24-1038 JUMMA MASJID ROAD, BUNDER MANGALORE 575001 0000000000VQA0032687 135.00 8 A NATARAJAN ANUGRAHA 9 SUBADRAL STREET TRIPLICANE CHENNAI 600005 0000000000VQA0042317 135.00 9 A GAYATHRI BHASKARAAN 48/B16 GIRIAPPA ROAD T NAGAR CHENNAI 600017 0000000000VQA0041978 135.00 10 A VATSALA BHASKARAN 48/B16 GIRIAPPA ROAD T NAGAR CHENNAI 600017 0000000000VQA0041977 135.00 11 A DHEENADAYALAN 14 AND 15 BALASUBRAMANI STREET GAJAVINAYAGA CITY, VENKATAPURAM CHENNAI, TAMILNADU 600053 0000IN30154914678295 1,350.00 12 A AYINAN NO 34 JEEVANANDAM STREET VINAYAKAPURAM AMBATTUR CHENNAI 600053 0000000000VQA0042517 135.00 13 A RAJASHANMUGA SUNDARAM NO 5 THELUNGU STREET ORATHANADU POST AND TK THANJAVUR 614625 0000IN30177414782892 180.00 14 A PALANICHAMY 1 / 28B ANNA COLONY KONAR CHATRAM MALLIYAMPATTU POST TRICHY 620102 0000IN30108022454737 112.50 15 A Vasanthi W/o G
    [Show full text]
  • Advertisement
    REPUBLIC OF KENYA SELECTION PANEL FOR THE APPOINTMENT OF COMMISSIONERS OF THE INDEPENDENT ELECTORAL AND BOUNDARIES COMMISSION ADVERTISEMENT PUBLICATION OF NAMES AND QUALIFICATIONS OF ALL APPLICANTS FOR THE POSITIONS OF CHAIRPERSON AND MEMBER OF THE INDEPENDENT ELECTORAL AND BOUNDARIES COMMISSION PURSUANT to Articles 88, 166(3) and 250 of the Constitution of Kenya, 2010, sections 5 and 6 of the Independent Electoral and Boundaries Commission Act, 2011 and Paragraph 3 of the First Schedule thereto, and the First Schedule of the Election Laws (Amendment) Act, 2016, the Selection Panel for the Appointment of Commissioners of the Independent Electoral and Boundaries Commission (IEBC) hereby publishes the names of all applicants who have applied for the positions of Chairperson and Member of the IEBC and their qualifications.* *This is a summary of the qualifications of these applicants. The applicants may have other qualifications. 1. APPLICATIONS FOR CHAIRPERSON OF THE IEBC (Ref. SP/IEBC/1/2016) S/NO NAME GENDER I.D/ COUNTY QUALIFICATIONS PP NO. 1. Andrew M 440999706 American PhD, International Law, New Jonathan York Law School Franklin BBA, Bernard M. Baruch College, City University of NY 2. David Mukii M 343680 Murang’a LLM, UON Mereka LLB, UON Page 1 of 119 S/NO NAME GENDER I.D/ COUNTY QUALIFICATIONS PP NO. 3. John Kangu M 0675657 Kakamega PhD Law, University of the Mutakha ( Dr.) Western Cape LLM, UNISA LLB, UON Dip. Legal Practice, KSL 4. John Tentemo M 9743660 Kajiado MA (Economics), UON Ole Moyaki BA, Moi University 5. Joshua M 23647427 Nyeri MBA, Strategic Management, Kamwere UON Wanjiku B.Comm (Accounting), CUEA CPA (K), KASNEB 6.
    [Show full text]
  • Strong Edge Graceful Labeling of Windmill Graphs ∑
    International Journal of Mathematics Research. ISSN 0976-5840 Volume 5, Number 1 (2013), pp. 19-26 © International Research Publication House http://www.irphouse.com Strong Edge Graceful Labeling of Windmill Graphs Dr. M. Subbiah VKS College Of Engineering& Technology Desiyamangalam, Karur - 639120 [email protected]. Abstract A (p, q) graph G is said to have strong edge graceful labeling if there 3q exists an injection f from the edge set to 1,2, ... so that the 2 induced mapping f+ defined on the vertex set given by f x fxy xy EG mod 2p are distinct. A graph G is said to be strong edge graceful if it admits a strong edge graceful labeling. In this paper we investigate strong edge graceful labeling of Windmill graph. (n) Definition: The windmill graphs Km (n >3) to be the family of graphs consisting of n copies of Km with a vertex in common. (n) Theorem: 1. The windmill graph K4 is strong edge graceful for all n 3 when n is even. (n) Proof: Let {v1, v2, v3, ..., v3n, } be the vertices of K4 and {e1, e2, e3, ...,e3n- (n) 1, e3n, , f1, ,f2, ,f3, . .f3n-1, f3n. } be the edges of K4 which are denoted as in the following Fig. 1. 20 Dr. M. Subbiah . v e 3 3 n n -1 . -1 . v . 3 n f . 3 n -2 f 3 e n . 3 -1 n e 3 2 n n -2 f v v 3 3n 0 2 v 3 . n-2 f v 1 . 2 f 2 f 3 f .
    [Show full text]
  • 5Th Lecture : Modular Decomposition MPRI 2013–2014 Schedule A
    5th Lecture : Modular decomposition MPRI 2013–2014 5th Lecture : Modular decomposition MPRI 2013–2014 Schedule 5th Lecture : Modular decomposition Introduction MPRI 2013–2014 Graph searches Michel Habib Applications of LBFS on structured graph classes [email protected] http://www.liafa.univ-Paris-Diderot.fr/~habib Chordal graphs Cograph recognition Sophie Germain, 22 octobre 2013 A nice conjecture 5th Lecture : Modular decomposition MPRI 2013–2014 5th Lecture : Modular decomposition MPRI 2013–2014 Introduction A hierarchy of graph models 1. Undirected graphs (graphes non orient´es) 2. Tournaments (Tournois), sometimes 2-circuits are allowed. 3. Signed graphs (Graphes sign´es) each edge is labelled + or - (for example friend or enemy) Examen le mardi 26 novembre de 9h `a12h 4. Oriented graphs (Graphes orient´es), each edge is given a Salle habituelle unique direction (no 2-circuits) An interesting subclass are the DAG Directed Acyclic Graphs (graphes sans circuit), for which the transitive closure is a partial order (ordre partiel) 5. Partial orders and comparability graphs an intersting particular case. Duality comparability – cocomparability (graphes de comparabilit´e– graphes d’incomparabilit´e) 6. Directed graphs or digraphs (Graphes dirig´es) 5th Lecture : Modular decomposition MPRI 2013–2014 5th Lecture : Modular decomposition MPRI 2013–2014 Introduction Introduction The problem has to be defined in each model and sometimes it could be hard. ◮ What is the right notion for a coloration in a directed graph ? For partial orders, comparability graphs or uncomparability graphs ◮ No directed cycle unicolored, seems to be the good one. the independant set and maximum clique problems are polynomial. ◮ It took 20 years to find the right notion of oriented matro¨ıd ◮ What is the right notion of treewidth for directed graphs ? ◮ Still an open question.
    [Show full text]
  • CIN/BCIN Company/Bank Name Date of AGM(DD-MON-YYYY)
    Note: This sheet is applicable for uploading the particulars related to the unclaimed and unpaid amount pending with company. Make sure that the details are in accordance with the information already provided in e-form IEPF-2 L85195TG1984PLC004507 Date Of AGM(DD-MON-YYYY) CIN/BCIN Prefill Company/Bank Name DR.REDDY'S LABORATORIES LTD 27-JUL-2018 Sum of unpaid and unclaimed dividend 5729595.00 Sum of interest on matured debentures 0.00 Sum of matured deposit 0.00 Sum of interest on matured deposit 0.00 Sum of matured debentures 0.00 Sum of interest on application money due for refund 0.00 Sum of application money due for refund 0.00 Redemption amount of preference shares 0.00 Sales proceed for fractional shares 0.00 Validate Clear Proposed Date of Investor First Investor Middle Investor Last Father/Husband Father/Husband Father/Husband Last DP Id-Client Id- Amount Address Country State District Pin Code Folio Number Investment Type transfer to IEPF Name Name Name First Name Middle Name Name Account Number transferred (DD-MON-YYYY) NEETA NARENDRA SHAH NA NA NA CHANDRIKA APT.,SHINGADA TALAV,W.NO.4016,,NASIKINDIA MAHARASHTRA NASIK DPID-CLID-1201750200019180Amount for unclaimed and unpaid dividend150.00 30-AUG-2020 ARUN KUMAR RADHAKRISHAN A-40,(60.MEATER),POCKET-00,,SECTOR-2,ROHINI,DELHIINDIA Delhi Delhi FOLIOA00001 Amount for unclaimed and unpaid dividend180.00 30-AUG-2020 AVINASH BALWANT DEV BALWANT 1 JASMIN APARTMENTS,NEW PANDITINDIA COLONY GANGAPURMAHARASHTRA ROAD,NASIK,NASIK NASIK FOLIOA00403 Amount for unclaimed and unpaid dividend60.00 30-AUG-2020 A RAVI KUMAR A KAMESWAR RAO DR.
    [Show full text]
  • Ifu Aur Main
    IRRFAN AND I Written by Vishal BhardwajTimes Delhi INT. MY HOME - DAY SUPER: 29TH APRIL 2020 It’s lockdown in Mumbai. I have been working from home for the past one month. The phone rings. It flashes M.P’s name on the screen. It gives me tremors. M.P is supposed to be my informer in Irrfan’s agency. I let the phone ring for a while and then take the call fearing the worst. A beat. M.P. He has started improving. Man, this guy is a hell of a fighter. Doctors are hopeful that he will bounce back. I take a deep breath and cut the line. LITTLE LATER I argue with Rekha for serving me less PANEER in last night’s dinner. I complain to her of being biased when it comes to choosing between me and Aasmaan. My phone beeps. I check my WhatsApp messenger (still bickering with Rekha). It’s a message from a friend from America. It reads - ‘Saddened to hear about Irrfan Khan’. I check my Twitter (Still squabbling fiercely with Rekha) to verify the authenticity of it. No news. I rule out the possibility. Times I bring myself to hear what Rekha is saying with tears in her eyes. REKHA What kind of pettiness is this? The phone rings again. It’s M.P once more. I pick it up hurriedly this time. There are sobs on the other side. A bomb explodesDelhi in my heart. CUT TO: EXT. ROAD TO GRAVEYARD - DAY Face masked with a N95 mask and hands covered with a pair of surgical gloves, I travel in my car on the deserted road leading to the Muslim cemetery.
    [Show full text]
  • Probable Deletions (PDF
    LIST OF PROBABLE ENTRIES IDENTIFIED TO BE DELETED FROM ELECTORAL ROLL DISTRICT NO & NAME :- 8 ERNAKULAM LAC NO & NAME :- 81 THRIPUNITHURA STATUS - S- SHIFT, E-EXPIRED , R- REPLICATION, M-MISSING, Q-DISQUALIFIED. LIST OF PROBABLE ENTRIES IDENTIFIED TO BE DELETED FROM ELECTORAL ROLL DISTRICT NO & NAME :- 8 ERNAKULAM LAC NO & NAME :- 81 THRIPUNITHURA PS NO & NAME :- 1 J.B.S Kundannoor (East side of Main Building) SL.NO NAME OF ELECTOR RLN RELATION NAME SEXAGEIDCARD_NO STATUS 3 Kevin J Pallan F Joyson M 22AFJ0317495 S 4 Lalitha H Purushan F 64KL/11/074/501616 S 5 Viju Kumar P P F Purushan M 40JGQ1509991 E 9 Mini H Surendran F 33JGQ1826536 R 23 Vimal N V F Varghese M 23AFJ0580050 R 41 Anilatmajan F Sivasankaran M 52KL/11/074/501064 S 42 Prameela H Anilatmajan F 45KL/11/074/501386 S 43 Akhil P A F Anilathmajan M 25AFJ0181446 S 44 Vanitha Babu F Babu Gopalan F 23AFJ0214544 R 76 Nalini H Sreedharan F 81KL/11/074/501463 E 104 Sanitha Sabu F Sabu F 24AFJ0279364 R 105 Chakkammu H Kocheetto F 84KL/11/074/501497 E 150 Karthikeyan F Ayichan M 79KL/11/074/501320 E 205Karuppan F Koran M 82KL/11/074/501618 E 225 ribin raj .P M regini.K.T M 25AFJ0193110 S 250 Mary Michael H Michael F 60AFJ0211797 S 280 Prabhakaran F Sankaran M 63KL/11/074/501101 S 281 Anandavalli H Prabhakaran F 57KL/11/074/501267 S 368 Govindharam K F Krishnan M 26AFJ0131110 S 382 Delish Raymond F Raymond M 24AFJ0181586 S 402Vimal F Viswanathan M 28JGQ1366806 S 403Vipin K.A.
    [Show full text]
  • (45-48) Devi to Diva
    GAP GYAN A GLOBAL JOURNAL OF SOCIAL SCIENCES ( ISSN – 2581-5830 ) Impact Factor – SJIF – 4.998, IIFS - 4.375 Globally peer-reviewed and open access journal. DEVI TO DIVA - A TRANSFORMATIONAL JOURNEY PORTRAYING WOMEN IN MAINSTREAM BOLLYWOOD Prof. Ms. Shivani Ahluwalia Orora, Sinhgad College of Commerce, Mumbai Abstract Bollywood is a major influence on Indian culture. It has shaped and expressed the changing scenarios of modern India .Hindi cinema has influenced the way in which people recognize various aspects of their own lives. Hindi cinema is largely been about stereotypes. The characters, situations and plots have been largely based on stereotypical ideologies. The audience reads the characters based on how they look, dress and talk. Over the years Indian cinema has portrayed women being ‘ The Satti Savitri, The Abla Nari ,The Sanskari ,The Wamp, to The Item Girls ,The Trophies ,The Bold beautiful and empathetic to The Ridiculed Modern women. “The paper begins with how bollywood is instrumental in shaping the culture and how it sketches womanhood. It also undertakes some glimpses from popular films to analyze the process of typecasting. A section is dedicated to the discussion on modern realistic women. In conclusion, a debate ensues on whether the mainstream cinema has been successful in portraying Indian women of different shades in a society dominated by patriarchal values. Keywords: Bollywood, Culture, Modern India, Stereotype, Womanhood, Patriarchal values. INTRODUCTION Women’s participation, performance and portrayal in media are the three important dimensions of study for the social science researchers of modern time, especially for the feminists. Because for the empowerment and development of the women section, it is very important to give them proper environment where they can raise their voices against the inequalities and the gender-gap they are experiencing in our male dominated or patriarchal societies.
    [Show full text]