DOCSLIB.ORG

18.04 Complex Analysis with Applications

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
18.04 Complex Analysis with Applications 18.04 Complex analysis with applications Spring 2019 lecture notes Instructor: J¨ornDunkel This PDF is an adaption and extension of the original by Andre Nachbin and Jeremy Orloff. Credit for course design and content should go to them; responsibility for typos and errors lies with me. 1 Contents 1 Brief course description 7 1.1 Topics needed from prerequisite math classes . .7 1.2 Level of mathematical rigor . .7 1.3 Speed of the class . .7 2 Complex algebra and the complex plane 8 2.1 Motivation . .8 2.2 Fundamental theorem of algebra . .8 2.3 Terminology and basic arithmetic . .9 2.4 The complex plane . 10 2.4.1 The geometry of complex numbers . 10 2.4.2 The triangle inequality . 10 2.5 Polar coordinates . 11 2.6 Euler's Formula . 12 2.6.1 eiθ behaves like a true exponential . 12 2.6.2 Complex exponentials and polar form . 13 2.6.3 Complexification or complex replacement . 15 2.6.4 Nth roots . 16 2.6.5 The geometry of Nth roots . 17 2.7 Inverse Euler formula . 18 2.8 de Moivre's formula . 18 2.9 Representing complex multiplication as matrix multiplication . 18 3 Complex functions 19 3.1 The exponential function . 19 3.2 Complex functions as mappings . 20 3.3 The function arg(z)............................... 25 3.3.1 Many-to-one functions . 25 3.3.2 Branches of arg(z)............................ 26 3.3.3 The principal branch of arg(z)..................... 28 3.4 Concise summary of branches and branch cuts . 29 3.5 The function log(z)................................ 29 3.5.1 Figures showing w = log(z) as a mapping . 30 3.5.2 Complex powers . 32 4 Analytic functions 33 4.1 The derivative: preliminaries . 33 4.2 Open disks, open deleted disks, open regions . 34 4.3 Limits and continuous functions . 35 4.3.1 Properties of limits . 36 4.3.2 Continuous functions . 36 4.3.3 Properties of continuous functions . 37 4.4 The point at infinity . 38 4.4.1 Limits involving infinity . 38 2 4.4.2 Stereographic projection from the Riemann sphere . 39 4.5 Derivatives . 40 4.5.1 Derivative rules . 40 4.6 Cauchy-Riemann equations . 41 4.6.1 Partial derivatives as limits . 41 4.6.2 The Cauchy-Riemann equations . 42 4.6.3 Using the Cauchy-Riemann equations . 43 4.6.4 f 0(z) as a 2 2 matrix . 44 × 4.7 Geometric interpretation & linear elasticity theory . 45 4.8 Cauchy-Riemann all the way down . 46 4.9 Gallery of functions . 47 4.9.1 Gallery of functions, derivatives and properties . 47 4.9.2 A few proofs . 51 4.10 Branch cuts and function composition . 52 4.11 Appendix: Limits . 54 4.11.1 Limits of sequences . 54 4.11.2 lim f(z)................................. 56 z!z0 4.11.3 Connection between limits of sequences and limits of functions . 56 5 Line integrals and Cauchy's theorem 56 5.1 Complex line integrals . 57 5.2 Fundamental theorem for complex line integrals . 58 5.3 Path independence . 59 5.4 Examples . 60 5.5 Cauchy's theorem . 61 5.6 Extensions of Cauchy's theorem . 64 6 Cauchy's integral formula 67 6.1 Cauchy's integral for functions . 67 6.2 Cauchy's integral formula for derivatives . 69 6.2.1 Another approach to some basic examples . 70 6.2.2 More examples . 70 6.2.3 The triangle inequality for integrals . 73 6.3 Proof of Cauchy's integral formula . 75 6.3.1 A useful theorem . 75 6.3.2 Proof of Cauchy's integral formula . 76 6.4 Proof of Cauchy's integral formula for derivatives . 77 6.5 Consequences of Cauchy's integral formula . 78 6.5.1 Existence of derivatives . 78 6.5.2 Cauchy's inequality . 78 6.5.3 Liouville's theorem . 79 6.5.4 Maximum modulus principle . 80 3 7 Introduction to harmonic functions 82 7.1 Harmonic functions . 83 7.2 Del notation . 83 7.2.1 Analytic functions have harmonic pieces . 83 7.2.2 Harmonic conjugates . 85 7.3 A second proof that u and v are harmonic . 85 7.4 Maximum principle and mean value property . 86 7.5 Orthogonality of curves . 86 8 Two dimensional hydrodynamics and complex potentials 90 8.1 Velocity fields . 91 8.2 Stationary flows . 91 8.3 Physical assumptions, mathematical consequences . 92 8.3.1 Physical assumptions . 92 8.3.2 Examples . 93 8.3.3 Summary . 94 8.4 Complex potentials . 94 8.4.1 Analytic functions give us incompressible, irrotational flows . 94 8.4.2 Incompressible, irrotational flows always have complex potential func- tions . 95 8.5 Stream functions . 96 8.5.1 Examples . 97 8.5.2 Stagnation points . 99 8.6 More examples . 99 9 Taylor and Laurent series 102 9.1 Geometric series . 103 9.1.1 Connection to Cauchy's integral formula . 104 9.2 Convergence of power series . 104 9.2.1 Ratio test and root test . 105 9.3 Taylor series . 106 9.3.1 Order of a zero . 106 9.3.2 Taylor series examples . 107 9.3.3 Proof of Taylor's theorem . 111 9.4 Singularities . 112 9.5 Laurent series . 112 9.5.1 Examples of Laurent series . 115 9.6 Digression to differential equations . 117 9.7 Poles . 118 9.7.1 Examples of poles . 119 9.7.2 Residues . 120 4 10 Residue Theorem 121 10.1 Poles and zeros . 121 10.2 Words: Holomorphic and meromorphic . 122 10.3 Behavior of functions near zeros and poles . 122 10.3.1 Picard's theorem and essential singularities . 123 10.3.2 Quotients of functions . 123 10.4 Residues . 124 10.4.1 Residues at simple poles ..
Load more

Recommended publications
  • Integration in the Complex Plane (Zill & Wright Chapter
    Integration in the Complex Plane (Zill & Wright Chapter 18) 1016-420-02: Complex Variables∗ Winter 2012-2013 Contents 1 Contour Integrals 2 1.1 Definition and Properties . 2 1.2 Evaluation . 3 1.2.1 Example: R z¯ dz ............................. 3 C1 1.2.2 Example: R z¯ dz ............................. 4 C2 R 2 1.2.3 Example: C z dz ............................. 4 1.3 The ML Limit . 5 1.4 Circulation and Flux . 5 2 The Cauchy-Goursat Theorem 7 2.1 Integral Around a Closed Loop . 7 2.2 Independence of Path for Analytic Functions . 8 2.3 Deformation of Closed Contours . 9 2.4 The Antiderivative . 10 3 Cauchy's Integral Formulas 12 3.1 Cauchy's Integral Formula . 12 3.1.1 Example #1 . 13 3.1.2 Example #2 . 13 3.2 Cauchy's Integral Formula for Derivatives . 14 3.3 Consequences of Cauchy's Integral Formulas . 16 3.3.1 Cauchy's Inequality . 16 3.3.2 Liouville's Theorem . 16 ∗Copyright 2013, John T. Whelan, and all that 1 Tuesday 18 December 2012 1 Contour Integrals 1.1 Definition and Properties Recall the definition of the definite integral Z xF X f(x) dx = lim f(xk) ∆xk (1.1) ∆xk!0 xI k We'd like to define a similar concept, integrating a function f(z) from some point zI to another point zF . The problem is that, since zI and zF are points in the complex plane, there are different ways to get between them, and adding up the value of the function along one path will not give the same result as doing it along another path, even if they have the same endpoints.
    [Show full text]
  • Informal Lecture Notes for Complex Analysis
    Informal lecture notes for complex analysis Robert Neel I'll assume you're familiar with the review of complex numbers and their algebra as contained in Appendix G of Stewart's book, so we'll pick up where that leaves off. 1 Elementary complex functions In one-variable real calculus, we have a collection of basic functions, like poly- nomials, rational functions, the exponential and log functions, and the trig functions, which we understand well and which serve as the building blocks for more general functions. The same is true in one complex variable; in fact, the real functions we just listed can be extended to complex functions. 1.1 Polynomials and rational functions We start with polynomials and rational functions. We know how to multiply and add complex numbers, and thus we understand polynomial functions. To be specific, a degree n polynomial, for some non-negative integer n, is a function of the form n n−1 f(z) = cnz + cn−1z + ··· + c1z + c0; 3 where the ci are complex numbers with cn 6= 0. For example, f(z) = 2z + (1 − i)z + 2i is a degree three (complex) polynomial. Polynomials are clearly defined on all of C. A rational function is the quotient of two polynomials, and it is defined everywhere where the denominator is non-zero. z2+1 Example: The function f(z) = z2−1 is a rational function. The denomina- tor will be zero precisely when z2 = 1. We know that every non-zero complex number has n distinct nth roots, and thus there will be two points at which the denominator is zero.
    [Show full text]
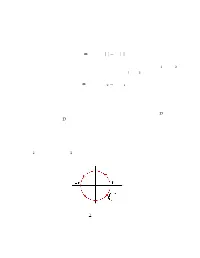
  • MATH 305 Complex Analysis, Spring 2016 Using Residues to Evaluate Improper Integrals Worksheet for Sections 78 and 79
    MATH 305 Complex Analysis, Spring 2016 Using Residues to Evaluate Improper Integrals Worksheet for Sections 78 and 79 One of the interesting applications of Cauchy's Residue Theorem is to find exact values of real improper integrals. The idea is to integrate a complex rational function around a closed contour C that can be arbitrarily large. As the size of the contour becomes infinite, the piece in the complex plane (typically an arc of a circle) contributes 0 to the integral, while the part remaining covers the entire real axis (e.g., an improper integral from −∞ to 1). An Example Let us use residues to derive the formula p Z 1 x2 2 π 4 dx = : (1) 0 x + 1 4 Note the somewhat surprising appearance of π for the value of this integral. z2 First, let f(z) = and let C = L + C be the contour that consists of the line segment L z4 + 1 R R R on the real axis from −R to R, followed by the semi-circle CR of radius R traversed CCW (see figure below). Note that C is a positively oriented, simple, closed contour. We will assume that R > 1. Next, notice that f(z) has two singular points (simple poles) inside C. Call them z0 and z1, as shown in the figure. By Cauchy's Residue Theorem. we have I f(z) dz = 2πi Res f(z) + Res f(z) C z=z0 z=z1 On the other hand, we can parametrize the line segment LR by z = x; −R ≤ x ≤ R, so that I Z R x2 Z z2 f(z) dz = 4 dx + 4 dz; C −R x + 1 CR z + 1 since C = LR + CR.
    [Show full text]
  • 1 the Complex Plane
    Math 135A, Winter 2012 Complex numbers 1 The complex numbers C are important in just about every branch of mathematics. These notes present some basic facts about them. 1 The Complex Plane A complex number z is given by a pair of real numbers x and y and is written in the form z = x+iy, where i satisfies i2 = −1. The complex numbers may be represented as points in the plane, with the real number 1 represented by the point (1; 0), and the complex number i represented by the point (0; 1). The x-axis is called the \real axis," and the y-axis is called the \imaginary axis." For example, the complex numbers 1, i, 3 + 4i and 3 − 4i are illustrated in Fig 1a. 3 + 4i 6 + 4i 2 + 3i imag i 4 + i 1 real 3 − 4i Fig 1a Fig 1b Complex numbers are added in a natural way: If z1 = x1 + iy1 and z2 = x2 + iy2, then z1 + z2 = (x1 + x2) + i(y1 + y2) (1) It's just vector addition. Fig 1b illustrates the addition (4 + i) + (2 + 3i) = (6 + 4i). Multiplication is given by z1z2 = (x1x2 − y1y2) + i(x1y2 + x2y1) Note that the product behaves exactly like the product of any two algebraic expressions, keeping in mind that i2 = −1. Thus, (2 + i)(−2 + 4i) = 2(−2) + 8i − 2i + 4i2 = −8 + 6i We call x the real part of z and y the imaginary part, and we write x = Re z, y = Im z.(Remember: Im z is a real number.) The term \imaginary" is a historical holdover; it took mathematicians some time to accept the fact that i (for \imaginary," naturally) was a perfectly good mathematical object.
    [Show full text]
  • Arxiv:1207.1472V2 [Math.CV]
    SOME SIMPLIFICATIONS IN THE PRESENTATIONS OF COMPLEX POWER SERIES AND UNORDERED SUMS OSWALDO RIO BRANCO DE OLIVEIRA Abstract. This text provides very easy and short proofs of some basic prop- erties of complex power series (addition, subtraction, multiplication, division, rearrangement, composition, differentiation, uniqueness, Taylor’s series, Prin- ciple of Identity, Principle of Isolated Zeros, and Binomial Series). This is done by simplifying the usual presentation of unordered sums of a (countable) family of complex numbers. All the proofs avoid formal power series, double series, iterated series, partial series, asymptotic arguments, complex integra- tion theory, and uniform continuity. The use of function continuity as well as epsilons and deltas is kept to a mininum. Mathematics Subject Classification: 30B10, 40B05, 40C15, 40-01, 97I30, 97I80 Key words and phrases: Power Series, Multiple Sequences, Series, Summability, Complex Analysis, Functions of a Complex Variable. Contents 1. Introduction 1 2. Preliminaries 2 3. Absolutely Convergent Series and Commutativity 3 4. Unordered Countable Sums and Commutativity 5 5. Unordered Countable Sums and Associativity. 9 6. Sum of a Double Sequence and The Cauchy Product 10 7. Power Series - Algebraic Properties 11 8. Power Series - Analytic Properties 14 References 17 arXiv:1207.1472v2 [math.CV] 27 Jul 2012 1. Introduction The objective of this work is to provide a simplification of the theory of un- ordered sums of a family of complex numbers (in particular, for a countable family of complex numbers) as well as very easy proofs of basic operations and properties concerning complex power series, such as addition, scalar multiplication, multipli- cation, division, rearrangement, composition, differentiation (see Apostol [2] and Vyborny [21]), Taylor’s formula, principle of isolated zeros, uniqueness, principle of identity, and binomial series.
    [Show full text]
  • The Integral Resulting in a Logarithm of a Complex Number Dr. E. Jacobs in first Year Calculus You Learned About the Formula: Z B 1 Dx = Ln |B| − Ln |A| a X
    The Integral Resulting in a Logarithm of a Complex Number Dr. E. Jacobs In first year calculus you learned about the formula: Z b 1 dx = ln jbj ¡ ln jaj a x It is natural to want to apply this formula to contour integrals. If z1 and z2 are complex numbers and C is a path connecting z1 to z2, we would expect that: Z 1 dz = log z2 ¡ log z1 C z However, you are about to see that there is an interesting complication when we take the formula for the integral resulting in logarithm and try to extend it to the complex case. First of all, recall that if f(z) is an analytic function on a domain D and C is a closed loop in D then : I f(z) dz = 0 This is referred to as the Cauchy-Integral Theorem. So, for example, if C His a circle of radius r around the origin we may conclude immediately that 2 2 C z dz = 0 because z is an analytic function for all values of z. H If f(z) is not analytic then C f(z) dz is not necessarily zero. Let’s do an 1 explicit calculation for f(z) = z . If we are integrating around a circle C centered at the origin, then any point z on this path may be written as: z = reiθ H 1 iθ Let’s use this to integrate C z dz. If z = re then dz = ireiθ dθ H 1 Now, substitute this into the integral C z dz.
    [Show full text]
  • Complex Sinusoids Copyright C Barry Van Veen 2014
    Complex Sinusoids Copyright c Barry Van Veen 2014 Feel free to pass this ebook around the web... but please do not modify any of its contents. Thanks! AllSignalProcessing.com Key Concepts 1) The real part of a complex sinusoid is a cosine wave and the imag- inary part is a sine wave. 2) A complex sinusoid x(t) = AejΩt+φ can be visualized in the complex plane as a vector of length A that is rotating at a rate of Ω radians per second and has angle φ relative to the real axis at time t = 0. a) The projection of the complex sinusoid onto the real axis is the cosine A cos(Ωt + φ). b) The projection of the complex sinusoid onto the imaginary axis is the cosine A sin(Ωt + φ). AllSignalProcessing.com 3) The output of a linear time invariant system in response to a com- plex sinusoid input is a complex sinusoid of the of the same fre- quency. The system only changes the amplitude and phase of the input complex sinusoid. a) Arbitrary input signals are represented as weighted sums of complex sinusoids of different frequencies. b) Then, the output is a weighted sum of complex sinusoids where the weights have been multiplied by the complex gain of the system. 4) Complex sinusoids also simplify algebraic manipulations. AllSignalProcessing.com 5) Real sinusoids can be expressed as a sum of a positive and negative frequency complex sinusoid. 6) The concept of negative frequency is not physically meaningful for real data and is an artifact of using complex sinusoids.
    [Show full text]
  • Complex Logarithm
    Complex Analysis Math 214 Spring 2014 Fowler 307 MWF 3:00pm - 3:55pm c 2014 Ron Buckmire http://faculty.oxy.edu/ron/math/312/14/ Class 14: Monday February 24 TITLE The Complex Logarithm CURRENT READING Zill & Shanahan, Section 4.1 HOMEWORK Zill & Shanahan, §4.1.2 # 23,31,34,42 44*; SUMMARY We shall return to the murky world of branch cuts as we expand our repertoire of complex functions when we encounter the complex logarithm function. The Complex Logarithm log z Let us define w = log z as the inverse of z = ew. NOTE Your textbook (Zill & Shanahan) uses ln instead of log and Ln instead of Log . We know that exp[ln |z|+i(θ+2nπ)] = z, where n ∈ Z, from our knowledge of the exponential function. So we can define log z =ln|z| + i arg z =ln|z| + i Arg z +2nπi =lnr + iθ where r = |z| as usual, and θ is the argument of z If we only use the principal value of the argument, then we define the principal value of log z as Log z, where Log z =ln|z| + i Arg z = Log |z| + i Arg z Exercise Compute Log (−2) and log(−2), Log (2i), and log(2i), Log (−4) and log(−4) Logarithmic Identities z = elog z but log ez = z +2kπi (Is this a surprise?) log(z1z2) = log z1 + log z2 z1 log = log z1 − log z2 z2 However these do not neccessarily apply to the principal branch of the logarithm, written as Log z. (i.e. is Log (2) + Log (−2) = Log (−4)? 1 Complex Analysis Worksheet 14 Math 312 Spring 2014 Log z: the Principal Branch of log z Log z is a single-valued function and is analytic in the domain D∗ consisting of all points of the complex plane except for those lying on the nonpositive real axis, where d 1 Log z = dz z Sketch the set D∗ and convince yourself that it is an open connected set.
    [Show full text]
  • Complex Analysis
    Complex Analysis Andrew Kobin Fall 2010 Contents Contents Contents 0 Introduction 1 1 The Complex Plane 2 1.1 A Formal View of Complex Numbers . .2 1.2 Properties of Complex Numbers . .4 1.3 Subsets of the Complex Plane . .5 2 Complex-Valued Functions 7 2.1 Functions and Limits . .7 2.2 Infinite Series . 10 2.3 Exponential and Logarithmic Functions . 11 2.4 Trigonometric Functions . 14 3 Calculus in the Complex Plane 16 3.1 Line Integrals . 16 3.2 Differentiability . 19 3.3 Power Series . 23 3.4 Cauchy's Theorem . 25 3.5 Cauchy's Integral Formula . 27 3.6 Analytic Functions . 30 3.7 Harmonic Functions . 33 3.8 The Maximum Principle . 36 4 Meromorphic Functions and Singularities 37 4.1 Laurent Series . 37 4.2 Isolated Singularities . 40 4.3 The Residue Theorem . 42 4.4 Some Fourier Analysis . 45 4.5 The Argument Principle . 46 5 Complex Mappings 47 5.1 M¨obiusTransformations . 47 5.2 Conformal Mappings . 47 5.3 The Riemann Mapping Theorem . 47 6 Riemann Surfaces 48 6.1 Holomorphic and Meromorphic Maps . 48 6.2 Covering Spaces . 52 7 Elliptic Functions 55 7.1 Elliptic Functions . 55 7.2 Elliptic Curves . 61 7.3 The Classical Jacobian . 67 7.4 Jacobians of Higher Genus Curves . 72 i 0 Introduction 0 Introduction These notes come from a semester course on complex analysis taught by Dr. Richard Carmichael at Wake Forest University during the fall of 2010. The main topics covered include Complex numbers and their properties Complex-valued functions Line integrals Derivatives and power series Cauchy's Integral Formula Singularities and the Residue Theorem The primary reference for the course and throughout these notes is Fisher's Complex Vari- ables, 2nd edition.
    [Show full text]
  • Complex Analysis (Princeton Lectures in Analysis, Volume
    COMPLEX ANALYSIS Ibookroot October 20, 2007 Princeton Lectures in Analysis I Fourier Analysis: An Introduction II Complex Analysis III Real Analysis: Measure Theory, Integration, and Hilbert Spaces Princeton Lectures in Analysis II COMPLEX ANALYSIS Elias M. Stein & Rami Shakarchi PRINCETON UNIVERSITY PRESS PRINCETON AND OXFORD Copyright © 2003 by Princeton University Press Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540 In the United Kingdom: Princeton University Press, 6 Oxford Street, Woodstock, Oxfordshire OX20 1TW All Rights Reserved Library of Congress Control Number 2005274996 ISBN 978-0-691-11385-2 British Library Cataloging-in-Publication Data is available The publisher would like to acknowledge the authors of this volume for providing the camera-ready copy from which this book was printed Printed on acid-free paper. ∞ press.princeton.edu Printed in the United States of America 5 7 9 10 8 6 To my grandchildren Carolyn, Alison, Jason E.M.S. To my parents Mohamed & Mireille and my brother Karim R.S. Foreword Beginning in the spring of 2000, a series of four one-semester courses were taught at Princeton University whose purpose was to present, in an integrated manner, the core areas of analysis. The objective was to make plain the organic unity that exists between the various parts of the subject, and to illustrate the wide applicability of ideas of analysis to other fields of mathematics and science. The present series of books is an elaboration of the lectures that were given. While there are a number of excellent texts dealing with individual parts of what we cover, our exposition aims at a different goal: pre- senting the various sub-areas of analysis not as separate disciplines, but rather as highly interconnected.
    [Show full text]
  • On Bounds of the Sine and Cosine Along Straight Lines on the Complex Plane
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 19 September 2018 doi:10.20944/preprints201809.0365.v1 Peer-reviewed version available at Acta Universitatis Sapientiae, Mathematica 2019, 11, 371-379; doi:10.2478/ausm-2019-0027 ON BOUNDS OF THE SINE AND COSINE ALONG STRAIGHT LINES ON THE COMPLEX PLANE FENG QI Institute of Mathematics, Henan Polytechnic University, Jiaozuo, Henan, 454010, China College of Mathematics, Inner Mongolia University for Nationalities, Tongliao, Inner Mongolia, 028043, China Department of Mathematics, College of Science, Tianjin Polytechnic University, Tianjin, 300387, China E-mail: [email protected], [email protected] URL: https: // qifeng618. wordpress. com Abstract. In the paper, the author discusses and computes bounds of the sine and cosine along straight lines on the complex plane. 1. Motivations In the theory of complex functions, the sine and cosine on the complex plane C are denoted and defined by eiz − e−iz e−iz + e−iz sin z = and cos z = ; 2i 2 where z = x + iy and x; y 2 R. When z = x 2 R, these two functions become sin x and cos x which satisfy the periodicity and boundedness sin(x + 2kπ) = sin x; cos(x + 2kπ) = cos x; j sin xj ≤ 1; j cos xj ≤ 1 for k 2 Z. On the other hand, when z = iy for y 2 R, e−y − ey e−y + ey sin(iy) = ! ±i1 and cos(iy) = ! +1 2i 2 as y ! ±∞. These imply that the sine and cosine are bounded on the real x-axis, but unbounded on the imaginary y-axis. Motivated by the above boundedness, we naturally guess that the complex func- tions sin z and cos z for z 2 C are (1) bounded on all straight lines parallel to the real x-axis, (2) unbounded on all straight lines whose slopes are not horizontal.
    [Show full text]
  • 4 Complex Analysis
    4 Complex Analysis “He is not a true man of science who does not bring some sympathy to his studies, and expect to learn something by behavior as well as by application. It is childish to rest in the discovery of mere coincidences, or of partial and extraneous laws. The study of geometry is a petty and idle exercise of the mind, if it is applied to no larger system than the starry one. Mathematics should be mixed not only with physics but with ethics; that is mixed mathematics. The fact which interests us most is the life of the naturalist. The purest science is still biographical.” Henry David Thoreau (1817 - 1862) We have seen that we can seek the frequency content of a signal f (t) defined on an interval [0, T] by looking for the the Fourier coefficients in the Fourier series expansion In this chapter we introduce complex numbers and complex functions. We a ¥ 2pnt 2pnt will later see that the rich structure of f (t) = 0 + a cos + b sin . 2 ∑ n T n T complex functions will lead to a deeper n=1 understanding of analysis, interesting techniques for computing integrals, and The coefficients can be written as integrals such as a natural way to express analog and dis- crete signals. 2 Z T 2pnt an = f (t) cos dt. T 0 T However, we have also seen that, using Euler’s Formula, trigonometric func- tions can be written in a complex exponential form, 2pnt e2pint/T + e−2pint/T cos = . T 2 We can use these ideas to rewrite the trigonometric Fourier series as a sum over complex exponentials in the form ¥ 2pint/T f (t) = ∑ cne , n=−¥ where the Fourier coefficients now take the form Z T −2pint/T cn = f (t)e dt.
    [Show full text]