Self-Generating Structures in Nature Based on Pneumatics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chassis Design for SAE Racer
University of Southern Queensland Faculty of Engineering and Surveying Chassis Design for SAE Racer A dissertation submitted by: Anthony M O’Neill In fulfilment of the requirements of ENG 4111/2 Research Project Towards the degree of Bachelor of Engineering (Mechanical) Submitted: October 2005 1 Abstract This dissertation concerns the design and construction of a chassis for the Formula SAE-Aust race vehicle – to be entered by the Motorsport Team of the University of Southern Queensland. The chassis chosen was the space frame – this was selected over the platform and unitary styles due to ease of manufacture, strength, reliability and cost. A platform chassis can be very strong, but at the penalty of excessive weight. The unitary chassis / body is very expensive to set up, and is generally used for large production runs or Formula 1 style vehicles. The space frame is simple to design and easy to fabricate – requiring only the skills and equipment found in a normal small engineering / welding workshop. The choice of material from which to make the space frame was from plain low carbon steel, AISI-SAE 4130 (‘chrome-moly’) or aluminium. The aluminium, though light, suffered from potential fatigue problems, and required precise heat / aging treatment after welding. The SAE 4130, though strong, is very expensive and also required proper heat treatment after welding, lest the joints be brittle. The plain low carbon steel met the structural requirements, did not need any heat treatments, and had the very real benefits of a low price and ready availability. It was also very economical to purchase in ERW (electric resistance welded) form, though CDS (cold drawn seamless) or DOM (drawn over mandrel) would have been preferable – though, unfortunately, much more expensive. -

The Making of the Sainsbury Centre the Making of the Sainsbury Centre
The Making of the Sainsbury Centre The Making of the Sainsbury Centre Edited by Jane Pavitt and Abraham Thomas 2 This publication accompanies the exhibition: Unless otherwise stated, all dates of built projects SUPERSTRUCTURES: The New Architecture refer to their date of completion. 1960–1990 Sainsbury Centre for Visual Arts Building credits run in the order of architect followed 24 March–2 September 2018 by structural engineer. First published in Great Britain by Sainsbury Centre for Visual Arts Norwich Research Park University of East Anglia Norwich, NR4 7TJ scva.ac.uk © Sainsbury Centre for Visual Arts, University of East Anglia, 2018 The moral rights of the authors have been asserted. All rights reserved. No part of this publication may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the publisher. British Library Cataloguing-in-Publication Data. A catalogue record is available from the British Library. ISBN 978 0946 009732 Exhibition Curators: Jane Pavitt and Abraham Thomas Book Design: Johnson Design Book Project Editor: Rachel Giles Project Curator: Monserrat Pis Marcos Printed and bound in the UK by Pureprint Group First edition 10 9 8 7 6 5 4 3 2 1 Superstructure The Making of the Sainsbury Centre for Visual Arts Contents Foreword David Sainsbury 9 Superstructures: The New Architecture 1960–1990 12 Jane Pavitt and Abraham Thomas Introduction 13 The making of the Sainsbury Centre 16 The idea of High Tech 20 Three early projects 21 The engineering tradition 24 Technology transfer and the ‘Kit of Parts’ 32 Utopias and megastructures 39 The corporate ideal 46 Conclusion 50 Side-slipping the Seventies Jonathan Glancey 57 Under Construction: Building the Sainsbury Centre 72 Bibliography 110 Acknowledgements 111 Photographic credits 112 6 Fo reword David Sainsbury Opposite. -
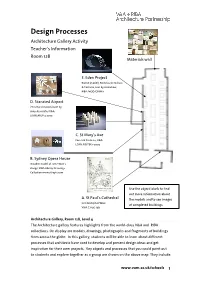
Exploring Skylines
Design Processes Architecture Gallery Activity Teacher’s Information Room 128 Materials wall E. Eden Project Biome (model), Nicholas Grimshaw & Partners, Lent by Grimshaw, RIBA: MOD/GRIM/1 D. Stansted Airport (Structural models) Lent by Arup Associates V&A: LOAN:ARUP.3-2003 C. St Mary’s Axe Foster & Partners, V&A: LOAN:FOSTER.1-2003 B. Sydney Opera House Wooden model of Jorn Utzon's design. RIBA Library Drawings Collection www.ribapix.com Use the object labels to find out more information about A. St Paul’s Cathedral the models and to see images Sir Christopher Wren of completed buildings. V&A: E.1195-1931 Architecture Gallery, Room 128, Level 4 The Architecture gallery features highlights from the world-class V&A and RIBA collections. On display are models, drawings, photographs and fragments of buildings from across the globe. In this gallery, students will be able to learn about different processes that architects have used to develop and present design ideas and get inspiration for their own projects. Key objects and processes that you could point out to students and explore together as a group are shown on the above map. They include: www.vam.ac.uk/schools 1 A. St Paul's Cathedral Drawing 1923-8 by R. B. Brook-Greaves (isometric projection) and W. Godfrey Allen London, England Pen and ink on paper, 3943 x 2747 mm Built 1675-1711 Given by Sir Mervyn Macartney Sir Christopher Wren (1632-1723) V&A: E.1195-1931 St Paul's Cathedral took 36 years to build. This magnificent drawing (which took draughtsmen more than four years to complete) shows how it is constructed. -

RIBA Annual Report 2019
A SUSTAINABLE FUTURE ANNUAL REPORT AND FINANCIAL STATEMENTS 31 DECEMBER 2019 RIBA was founded in 1834 for “the general advancement of civil architecture”. Our purpose is to deliver sustainable buildings and places, stronger communities and an inclusive environment for all. We rely on our members, supporters and charitable trading operations to make our work possible. We uphold the highest standards of professionalism and best practice. We value inclusion, collaboration, knowledge and progression, qualities that will enable our members to succeed, now and in the future. Our purpose is to deliver sustainable buildings and places, stronger communities and an inclusive environment for all. RIBA Annual Report and Financial Statements 2019 2 CONTENTS 1 2 A STRONG ORGANISATION A STRONG PROFESSION FOR WITH A BRIGHT FUTURE 10 A SUSTAINABLE SECTOR 20 Governance for a sustainable future 11 Leading the profession on climate 22 Maintaining financial strength 12 A Plan of Work for sustainable projects 23 A year of membership growth 13 Progress in continuing professional Supporting and developing our people 14 development 24 Digital investment for the long term 16 Creating new business for members 25 Becoming a truly global organisation 18 Fire safety for future generations 27 A brand for the future 19 Standing up for equality 28 Education for tomorrow’s profession 31 Engaging with architects everywhere 32 Setting the professional standard 37 3 4 A STRONG VOICE FOR FINANCIAL LASTING CHANGE 38 REVIEW 64 Speaking up for change 40 Financial review 64 Awards -

Structural Design of a Geodesic-Inspired Structure for Oculus: Solar Decathlon Africa 2019
Structural Design of a Geodesic-inspired Structure for Oculus: Solar Decathlon Africa 2019 A Major Qualifying Project submitted to the faculty of WORCESTER POLYTECHNIC INSTITUTE in partial fulfillment of the requirements for the Degree of Bachelor of Science Submitted By: Sara Cardona Mary Sheehan Alana Sher December 14, 2018 Submitted To: Tahar El-Korchi Nima Rahbar Steven Van Dessel Abstract The goal of this project was to create the structural design for a lightweight dome frame structure for the 2019 Solar Decathlon Africa competition in Morocco. The design consisted of developing member sizes and joint connections using both wood and steel. In order to create an innovative and competitive design we incorporated local construction materials and Moroccan architectural features. The result was a structure that would be a model for geodesic inspired homes that are adaptable and incorporate sustainable features. ii Acknowledgements Sincere thanks to our advisors Professors Tahar El-Korchi, Nima Rahbar, and Steven Van Dessel for providing us with feedback throughout our project process. Thank you to Professor Leonard Albano for assisting us with steel design and joint design calculations. Additionally, thank you to Kenza El-Korchi, a visiting student from Morocco, for helping with project coordination. iii Authorship This written report, as well as the design development process, was a collaborative effort. All team members, Sara Cardona, Mary Sheehan, and Alana Sher contributed equal efforts to this project. iv Capstone Design Statement This Major Qualifying Project (MQP) investigated the structural design of a lightweight geodesic-dome inspired structure for the Solar Decathlon Africa 2019 competition. The main design components of this project included: member sizing and verification using a steel and wood buckling analysis, and joint sizing using shear and bearing analysis. -

Design Method for Adaptive Daylight Systems for Buildings Covered by Large (Span) Roofs
Design method for adaptive daylight systems for buildings covered by large (span) roofs Citation for published version (APA): Heinzelmann, F. (2018). Design method for adaptive daylight systems for buildings covered by large (span) roofs. Technische Universiteit Eindhoven. Document status and date: Published: 12/06/2018 Document Version: Publisher’s PDF, also known as Version of Record (includes final page, issue and volume numbers) Please check the document version of this publication: • A submitted manuscript is the version of the article upon submission and before peer-review. There can be important differences between the submitted version and the official published version of record. People interested in the research are advised to contact the author for the final version of the publication, or visit the DOI to the publisher's website. • The final author version and the galley proof are versions of the publication after peer review. • The final published version features the final layout of the paper including the volume, issue and page numbers. Link to publication General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal. -

Governing Equations for Simulations of Soap Bubbles
University of California Merced Capstone Project Governing Equations For Simulations Of Soap Bubbles Author: Research Advisor: Ivan Navarro Fran¸cois Blanchette 1 Introduction The capstone project is an extension of work previously done by Fran¸coisBlanchette and Terry P. Bigioni in which they studied the coalescence of drops with either a hori- zontal reservoir or a drop of a different size (Blanchette and Bigioni, 2006). Specifically, they looked at the partial coalescence of a drop, which leaves behind a smaller "daugh- ter" droplet due to the incomplete merging process. Numerical simulations were used to study coalescence of a drop slowly coming into contact with a horizontal resevoir in which the fluid in the drop is the same fluid as that below the interface (Blanchette and Bigioni, 2006). The research conducted by Blanchette and Bigioni starts with a drop at rest on a flat interface. A drop of water will then merge with an underlying resevoir (water in this case), forming a single interface. Our research involves using that same numerical ap- proach only this time a soap bubble will be our fluid of interest. Soap bubbles differ from water drops on the fact that rather than having just a single interface, we now have two interfaces to take into account; the air inside the soap bubble along with the soap film on the boundary, and the soap film with any other fluid on the outside. Due to this double interface, some modifications will now be imposed on the boundary conditions involving surface tension along the interface. Also unlike drops, soap bubble thickness is finite which will mean we must keep track of it. -

Weighted Transparency: Literal and Phenomenal
Frei Otto soap bubble model (top left), Antonio Gaudi gravity model (bottom left), Miguel Fisac fabric form concrete wall (right) Weighted Transparency: Literal and Phenomenal SPRING 2020, OPTION STUDIO VISITING ASSOCIATE PROFESSOR NAOMI FRANGOS “As soon as we adventure on the paths of the physicist, we learn to weigh and to measure, to deal with time and space and mass and their related concepts, and to find more and more our knowledge expressed and our needs satisfied through the concept of number, as in the dreams and visions of Plato and Pythagoras; for modern chemistry would have gladdened the hearts of those great philosophic dreamers.” On Growth and Form, D’Arcy Wentworth Thompson Today’s maker architect is such a dreamt physicist. What is at stake is the ability to balance critical form-finding informed by the behavior of matter itself with the rigor of precision afforded by computational thinking. This studio transposes ideas of cross- disciplinarity in design, art, science, engineering and material studies pioneered by our forerunner master-builders into built prototypes by studying varying degrees of literal and phenomenal transparency achieved through notions of weight. Working primarily with a combination of plaster/concrete and glass/porcelain, juxtapositions are provoked between solid and void, heavy and light, opaque and transparent, smooth and textured, volume and surface. How can the actual weight of a material affect its sense of mass? How can mass capture the phenomena of weightlessness? How can physical material properties dictate appearances beyond optical transparency? Using dynamic matter/flexible formwork (i.e. salt, sand, gravel, fabric), suspended/submerged and compression/ expansion systems, weight plays a major role in deriving methods of fabrication and determining experiential qualities of made artifacts. -

Now on View in the Entrance of Art Los Angeles Contemporary, Ramada Santa Monica Is the Fourth Iteration in Mark Hagen's Serie
Now on view in the entrance of Art Los Angeles Contemporary, Ramada Santa Monica is the fourth iteration in Mark Hagen’s series of space frame installations—this time housing the catalog of materials from independent publisher Artbook | D.A.P. Aluminum triangles join into modular architectural units, towering floor to ceiling and enclosing a corner of the lobby, where polished fossils (in fact fossilized feces) act as bookends. We've seen the future and we're not going titles Hagen’s 2012 space frame work, that one affixed with rough slabs of obsidian. The pleasure of this uneasy pairing springs from its clever twinning of aesthetics and eras of technology: the irregular cuts of obsidian with the uniformity of the space frame, the material of prehistoric weaponry with the template for 1950s modular design. We’ve seen the future and we’re not going both rejects technological accelerationism and admits a melancholic truth: our utopian techno-future simply has not come. This ambivalence about technology, the failure of positivism to deliver on its promises, animates Hagen’s space frame sculptures, as they call out to (and become implicated in) the sinister evolution of the form. In the middle of the twentieth century, space frames were perfected by utopian architect Buckminster Fuller in his geodesic domes. Now, luxury car manufactures including Audi and Lamborghini advertise their use of the space frame, testifying to the recherché design. This evolution is unsurprising. Buckminster Fuller’s ideals of totalizing efficiency as well as neologisms like “synergy” find exquisite expression in corporate management; the hippie communes founded on his principles collapsed within the decade. -

Review on Study of Space Frame Structure System
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 07 Issue: 04 | Apr 2020 www.irjet.net p-ISSN: 2395-0072 Review on Study of Space Frame Structure System S. A. Ashtul1, S. N. Patil2 1PG Student, Department of Civil Engineering 2Assistant Professor, Department of Civil Engineering, Rajarambapu Institute of Technology, Maharashtra, India ---------------------------------------------------------------------***---------------------------------------------------------------------- Abstract - In the last few decades there was continuous these techniques concrete slab over the top chord which development in the construction industry. Mankind is always enhances the compression capacity and shows better attempted to utilize the maximum space for the structure. The performance of space frame structure [10]. need for modern structures is to achieve a large clear span The present paper focuses on the basic concept of a space with the economy. Now-days it is observed that there is a frame system. And also on the studies carried out by several growing interest in space frame systems. A space frame is a 3D researchers for understanding the structural behavior of the structural system in which well-organized linear axial space frame system by considering various parameters. elements are put together for the uniform distribution of forces. The main purpose to use these systems is to cover a large span area and giving a pleasant appearance to the 2. SPACE FRAME SYSTEM structure. Also, the space frames are light in weight and can easily be transported to the site. The objective of this paper is 2.1 Introduction to present the detailed concept of space frame systems and applications of these systems. -

Vibrations of Fractal Drums
VOLUME 67, NUMBER 21 PHYSICAL REVIEW LETTERS 18 NOVEMBER 1991 Vibrations of Fractal Drums B. Sapoval, Th. Gobron, and A. Margolina "' Laboratoire de Physique de la Matiere Condensee, Ecole Polytechnique, 91128 Palaiseau CEDEX, France (Received l7 July l991) Fractal boundary conditions drastically alter wave excitations. The low-frequency vibrations of a membrane bounded by a rigid fractal contour are observed and localized modes are found. The first lower eigenmodes are computed using an analogy between the wave and the diffusion equations. The fractal frontier induces a strong confinement of the wave analogous to superlocalization. The wave forms exhibit singular derivatives near the boundary. PACS numbers: 64.60.Ak, 03.40.Kf, 63.50.+x, 71.55.3v Objects with irregular geometry are ubiquitous in na- shown in Fig. 2. ture and their vibrational properties are of general in- The observation of confined modes was a surprise be- terest. For instance, the dependence of sea waves on the cause, in principle, the symmetry of the structure forbids topography of coastlines is a largely unanswered question. their existence. In fact, this experimental localization is The emergence of fractal geometry was a significant due both to damping and to the existence of narrow paths breakthrough in the description of irregularity [11. It has in the geometry of the membrane. If only one of the been suggested that the very existence of some of the equivalent regions like A is excited, then a certain time T, fractal structures found in nature is attributable to a called the delocalization time is necessary for the excita- self-stabilization due to their ability to damp harmonic tion to travel from A to B. -

Memoirs of a Bubble Blower
Memoirs of a Bubble Blower BY BERNARD ZUBROVVSKI Reprinted from Technology Review, Volume 85, Number 8, Nov/Dec 1982 Copyright 1982, Alumni Association of the Massachusetts Institute of Technolgy, Cambridge, Massachusetts 02139 EDUCATION A SPECIAL REPORT Memoirs N teaching science to children, I have dren go a step further by creating three- found that the best topics are those dimensional clusters of bubbles that rise I that are equally fascinating to chil• up a plexiglass tube. These bubbles are dren and adults alike. And learning is not as regular as those in the honeycomb most enjoyable when teacher and students formation, but closer observation reveals are exploring together. Blowing bubbles that they have a definite pattern: four provides just such qualities. bubbles (and never more than four) are Bubble blowing is an exciting and fruit• usually in direct contact with one another, ful way for children to develop basic in• with their surfaces meeting at a vertex at tuition in science and mathematics. And angles of about 109 degrees. And each working with bubbles has prompted me to of a bubble in the cluster will have roughly the wander into various scientific realms such same number of sides, a fact that turns out as surface physics, cellular biology, topol• to be scientifically significant. ogy, and architecture. Bubbles and soap Bubble In the 1940s, E.B. Matzke, a well- films are also aesthetically appealing, and known botanist who experimented with the children and I have discovered bubbles bubbles, discovered that bubbles in an to be ideal for making sculptures. In fact, array have an average of 14 sides.