DOCSLIB.ORG

Memoirs of a Bubble Blower

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Memoirs of a Bubble Blower Memoirs of a Bubble Blower BY BERNARD ZUBROVVSKI Reprinted from Technology Review, Volume 85, Number 8, Nov/Dec 1982 Copyright 1982, Alumni Association of the Massachusetts Institute of Technolgy, Cambridge, Massachusetts 02139 EDUCATION A SPECIAL REPORT Memoirs N teaching science to children, I have dren go a step further by creating three- found that the best topics are those dimensional clusters of bubbles that rise I that are equally fascinating to chil• up a plexiglass tube. These bubbles are dren and adults alike. And learning is not as regular as those in the honeycomb most enjoyable when teacher and students formation, but closer observation reveals are exploring together. Blowing bubbles that they have a definite pattern: four provides just such qualities. bubbles (and never more than four) are Bubble blowing is an exciting and fruit• usually in direct contact with one another, ful way for children to develop basic in• with their surfaces meeting at a vertex at tuition in science and mathematics. And angles of about 109 degrees. And each working with bubbles has prompted me to of a bubble in the cluster will have roughly the wander into various scientific realms such same number of sides, a fact that turns out as surface physics, cellular biology, topol• to be scientifically significant. ogy, and architecture. Bubbles and soap Bubble In the 1940s, E.B. Matzke, a well- films are also aesthetically appealing, and known botanist who experimented with the children and I have discovered bubbles bubbles, discovered that bubbles in an to be ideal for making sculptures. In fact, array have an average of 14 sides. That is, looking over the past ten years I can see a Blower the "average" bubble has the shape of a certain philosophy emerging—a sort of 14-sided polyhedron. And that's impor• Zen and the art of bubble blowing. tant because 14 is the number of faces of BY BERNARD ZUBRQWSKI the so-called "Kelvin cell." Proposed by Patterns in Bubbles Lord Kelvin in the late 1880s, this is the Shimmering ideal geometric shape for enclosing space, Adults tend to think of bubbles as a visual and intricate as they grow requiring the minimum surface area and phenomenon, but I suspect children are tension to enclose a given volume. initially more intrigued by their kinetic and change, soap bubbles This may seem to be another of those qualities. Soap film is very sensual as it fascinate nearly everyone. esoteric facts scientists bandy about, yet it expands, moving like Jello, sometimes bears on a wide range of structures. For with the entire bubble swaying from side And example, scientists have noted a consistent to side. In the film itself, amoebalike spots blowing bubbles is a rich similarity between soap-bubble arrays and swim through stratified layers of brilliant such diverse things as human fat cells, color. And there is a special quality— but overlooked approach to plant cells, cells of dragonfly wings, spots artistic? scientific?—in the way bubbles Imrning, providing insights on a giraffe, cracks in dried mud, the way clump together. Though they seem to have lead shot compacts, and the granular an intricate complexity, the bubbles in a in areas trom structure of metals. Peter Pearce, in Struc• cluster actually take only two basic the perceptual to ture in Nature Is a Strategy for Design, geometric configurations. the philasophieal. says that soap-bubble arrays "can be Such bubble behavior is featured in ex• taken as the model or type of all hibits I've developed at the Children's systems—biological, physical, chemical— Museum in Boston. In one exhibit, chil• BERNARD ZUBROWSKI is on the staff of the in which there is an economical associa• dren generate a froth of bubbles between Children's Museum in Boston. He holds an tion of cellular modules." What I hope M.S.T. in chemistry and education from Boston two plexiglass sheets spaced half an inch children will gain from playing with bub• College and is the author of numerous books apart. The bubbles form a two- bles is the realization that there are many that describe science experiments using house• patterns in both natural and human-made dimensional hexagonal array similar to a hold materials. Water Pumps and Syphons honeycomb, with three bubble surfaces (Little, Brown, 1981) won the New York phenomena, and that discovering and ex• always meeting along a line at angles of Academy of Sciences' 1982 award as the best plaining such patterns is a vital part of 120 degrees. In another exhibit, the chil- science book for young children. science. 2 Children "at work" at the arrays, such as the simple Children's Museum in Bos• cluster above, as struc• ton. Soap bubbles provide tural models. The Pneu vivid examples of many Dome (left) is an early geometric shapes and product of Crysalis Corp., spark discussions of designed for those who mathematical concepts. want a bubble in their Architects also use bubble backyard. EDUCATION A SPECIAL REPORT Architects have also capitalized on ment. The shapes that bubbles take are Though I am sure she could not have ex• bubbles as what Pearce calls "an elegant similar enough to encourage the search for plained exactly what she had generated, demonstration of minimal principles." patterns, yet they are always different her face and gestures indicated deep con• (Bees, nature's superb architects, demon• enough to arouse anticipation. These centration and satisfaction. strate minimal principles at work: the properties prove to be irresistable to configuration of a honeycomb contains almost everyone, from children in African Geometry in Action the greatest amount of honey with the villages to those in suburban Boston. The least amount of beeswax and requires the educational value is that the material, not On a conceptual level, bubbles can help least energy to construct.) Frei Otto of the teacher, is the motivator. This doesn't illustrate a variety of mathematical rela• Germany is a pioneer in this field, with negate the teacher's role, but suggests that tionships. In fact, mathematicians have numerous bubble-inspired structures to here is something worth exploring for its studied the principles governing the his credit: large balloonlike buildings and own sake. geometry of soap films for at least two huge tents with sweeping lines. Although These qualities were dramatized for me centuries. For younger children, bubbles Otto doesn't simply build a scaled-up as I blew bubbles with a blind child. He and their arrays serve as vivid examples of version of a small bubble array, he finds would wet one hand with soapy film and many geometric shapes, such as the soap-film models useful in determining then, by blowing through a straw, would sphere, hemisphere, pentagon, and hexa• such things as the minimal surface area form a bubble on his hand. He could sense gon. Creating and feeling these shapes is and the stresses that will occur in his when the bubble began forming and how much more dramatic than simply seeing structures. Indeed, "bubbles" are becom• big it grew. And when it broke, the warm them portrayed two-dimensionally in a ing an increasingly familiar sight in many air in the bubble would disperse—a clear drawing. With older children, bubbles will cities, with tennis courts and other athletic indication that it was gone. The boy grew spark discussions of concepts such as an• facilities sporting air-supported domes excited each time a bubble expanded to gles, surface areas, perimeters, and vol• based on the structure of bubble arrays. cover his hand, and afterward he umes of various geometric shapes. For So soap bubbles are useful in understand• exclaimed that he had never experienced example, by making a bubble grow larger ing structural arrangements from the bubbles so large. they can begin to see the relationship be• micro to the macro. In another instance, I videotaped chil• tween volume and diameter—often a dif• dren playing with the exhibits in the Chil• ficult concept to convey—and they can Lessons to See and Feel dren's Museum and observed a girl who make direct measurements to confirm spent 45 minutes with the same contrap• their observations. Having played with bubbles for so long tion. It was simply some sticks and string Indeed, I feel a bubbles "curriculum" with children, I am convinced that edu• that, when pulled out of the soapy water, could be developed that would span the cators are overlooking a rich opportunity. made a two-by-three-foot film. I discov• educational time line from preschool to Manipulating soap films involves both the ered that the girl developed a repertoire of postgraduate. Students can return to visual and the haptic senses; that is, what manipulations that produced a variety of bubbles time and again and delve more we see and how our bodies sense move• curved surfaces and geometric shapes. deeply into their geometry. This approach Soap films illustrate "min• pavilion at lower right, imal principles." The designed by Chrysalis machine above enables Corp., provides shade for designers to determine Kennedy Square in De• the surface area and troit. Any shape that bub• stresses in the structure bles or soap film take can produced by inverting the be duplicated in an air- soap film (upper right). filled or tentlike structure. The soap-film-inspired s EDUCATION A SPECIAL REPORT Bubbles in a cluster follow mathemat• ical laws and take only two basic geometric configurations. Three sur• faces can meet along a line at angles of 120 degrees, or the surfaces of four bubbles (never more than four) can meet at a vertex at angles of about 109 degrees.
Load more

Recommended publications
  • Governing Equations for Simulations of Soap Bubbles
    University of California Merced Capstone Project Governing Equations For Simulations Of Soap Bubbles Author: Research Advisor: Ivan Navarro Fran¸cois Blanchette 1 Introduction The capstone project is an extension of work previously done by Fran¸coisBlanchette and Terry P. Bigioni in which they studied the coalescence of drops with either a hori- zontal reservoir or a drop of a different size (Blanchette and Bigioni, 2006). Specifically, they looked at the partial coalescence of a drop, which leaves behind a smaller "daugh- ter" droplet due to the incomplete merging process. Numerical simulations were used to study coalescence of a drop slowly coming into contact with a horizontal resevoir in which the fluid in the drop is the same fluid as that below the interface (Blanchette and Bigioni, 2006). The research conducted by Blanchette and Bigioni starts with a drop at rest on a flat interface. A drop of water will then merge with an underlying resevoir (water in this case), forming a single interface. Our research involves using that same numerical ap- proach only this time a soap bubble will be our fluid of interest. Soap bubbles differ from water drops on the fact that rather than having just a single interface, we now have two interfaces to take into account; the air inside the soap bubble along with the soap film on the boundary, and the soap film with any other fluid on the outside. Due to this double interface, some modifications will now be imposed on the boundary conditions involving surface tension along the interface. Also unlike drops, soap bubble thickness is finite which will mean we must keep track of it.
    [Show full text]
  • Weighted Transparency: Literal and Phenomenal
    Frei Otto soap bubble model (top left), Antonio Gaudi gravity model (bottom left), Miguel Fisac fabric form concrete wall (right) Weighted Transparency: Literal and Phenomenal SPRING 2020, OPTION STUDIO VISITING ASSOCIATE PROFESSOR NAOMI FRANGOS “As soon as we adventure on the paths of the physicist, we learn to weigh and to measure, to deal with time and space and mass and their related concepts, and to find more and more our knowledge expressed and our needs satisfied through the concept of number, as in the dreams and visions of Plato and Pythagoras; for modern chemistry would have gladdened the hearts of those great philosophic dreamers.” On Growth and Form, D’Arcy Wentworth Thompson Today’s maker architect is such a dreamt physicist. What is at stake is the ability to balance critical form-finding informed by the behavior of matter itself with the rigor of precision afforded by computational thinking. This studio transposes ideas of cross- disciplinarity in design, art, science, engineering and material studies pioneered by our forerunner master-builders into built prototypes by studying varying degrees of literal and phenomenal transparency achieved through notions of weight. Working primarily with a combination of plaster/concrete and glass/porcelain, juxtapositions are provoked between solid and void, heavy and light, opaque and transparent, smooth and textured, volume and surface. How can the actual weight of a material affect its sense of mass? How can mass capture the phenomena of weightlessness? How can physical material properties dictate appearances beyond optical transparency? Using dynamic matter/flexible formwork (i.e. salt, sand, gravel, fabric), suspended/submerged and compression/ expansion systems, weight plays a major role in deriving methods of fabrication and determining experiential qualities of made artifacts.
    [Show full text]
  • Vibrations of Fractal Drums
    VOLUME 67, NUMBER 21 PHYSICAL REVIEW LETTERS 18 NOVEMBER 1991 Vibrations of Fractal Drums B. Sapoval, Th. Gobron, and A. Margolina "' Laboratoire de Physique de la Matiere Condensee, Ecole Polytechnique, 91128 Palaiseau CEDEX, France (Received l7 July l991) Fractal boundary conditions drastically alter wave excitations. The low-frequency vibrations of a membrane bounded by a rigid fractal contour are observed and localized modes are found. The first lower eigenmodes are computed using an analogy between the wave and the diffusion equations. The fractal frontier induces a strong confinement of the wave analogous to superlocalization. The wave forms exhibit singular derivatives near the boundary. PACS numbers: 64.60.Ak, 03.40.Kf, 63.50.+x, 71.55.3v Objects with irregular geometry are ubiquitous in na- shown in Fig. 2. ture and their vibrational properties are of general in- The observation of confined modes was a surprise be- terest. For instance, the dependence of sea waves on the cause, in principle, the symmetry of the structure forbids topography of coastlines is a largely unanswered question. their existence. In fact, this experimental localization is The emergence of fractal geometry was a significant due both to damping and to the existence of narrow paths breakthrough in the description of irregularity [11. It has in the geometry of the membrane. If only one of the been suggested that the very existence of some of the equivalent regions like A is excited, then a certain time T, fractal structures found in nature is attributable to a called the delocalization time is necessary for the excita- self-stabilization due to their ability to damp harmonic tion to travel from A to B.
    [Show full text]
  • Computer Graphics and Soap Bubbles
    Computer Graphics and Soap Bubbles Cheung Leung Fu & Ng Tze Beng Department of Mathematics National University of Singapore Singapore 0511 Soap Bubbles From years of study and of contemplation A boy, with bowl and straw, sits and blows, An old man brews a work of clarity, Filling with breath the bubbles from the bowl. A gay and involuted dissertation Each praises like a hymn, and each one glows; Discoursing on sweet wisdom playfully Into the filmy beads he blows his soul. An eager student bent on storming heights Old man, student, boy, all these three Has delved in archives and in libraries, Out of the Maya.. foam of the universe But adds the touch of genius when he writes Create illusions. None is better or worse A first book full of deepest subtleties. But in each of them the Light of Eternity Sees its reflection, and burns more joyfully. The Glass Bead Game Hermann Hesse The soap bubble, a wonderful toy for children, a motif for poetry, is at the same time a mathematical entity that has a fairly long history. Thanks to the advancement of computer graphics which led to solutions of decade-old conjectures, 'soap bubbles' have become once again a focus of much mathematical research in recent years. Anyone who has seen or played with a soap bubble knows that it is a spherical object. It is indeed a sphere if one defines a soap bubble to be a surface minimizing the area among all surfaces enclosing the same given volume. Relaxing this condition, mathematicians defined a soap bubble or surface of constant mean curvature to be a surface which is locally the stationary point of the area function when compared again locally to neighbouring surfaces enclosing the same volume.
    [Show full text]
  • Graphs in Nature
    Graphs in Nature David Eppstein University of California, Irvine Algorithms and Data Structures Symposium (WADS) August 2019 Inspiration: Steinitz's theorem Purely combinatorial characterization of geometric objects: Graphs of convex polyhedra are exactly the 3-vertex-connected planar graphs Image: Kluka [2006] Overview Cracked surfaces, bubble foams, and crumpled paper also form natural graph-like structures What properties do these graphs have? How can we recognize and synthesize them? I. Cracks and Needles Motorcycle graphs: Canonical quad mesh partitioning Problem: partition irregular quad-mesh into regular submeshes [Eppstein et al. 2008] Inspiration: Light cycle game from TRON movies Mesh partitioning method Grow cut paths outwards from each irregular (non-degree-4) vertex Cut paths continue straight across regular (degree-4) vertices They stop when they run into another path Result: approximation to optimal partition (exact optimum is NP-complete) Mesh-free motorcycle graphs Earlier... Motorcycles move from initial points with given velocities When they hit trails of other motorcycles, they crash [Eppstein and Erickson 1999] Application of mesh-free motorcycle graphs Initially: A simplified model of the inward movement of reflex vertices in straight skeletons, a rectilinear variant of medial axes with applications including building roof construction, folding and cutting problems, surface interpolation, geographic analysis, and mesh construction Later: Subroutine for constructing straight skeletons of simple polygons [Cheng and Vigneron 2007; Huber and Held 2012] Image: Huber [2012] Construction of mesh-free motorcycle graphs Main ideas: Define asymmetric distance: Time when one motorcycle would crash into another's trail Repeatedly find closest pair and eliminate crashed motorcycle Image: Dancede [2011] O(n17=11+) [Eppstein and Erickson 1999] Improved to O(n4=3+) [Vigneron and Yan 2014] Additional log speedup using mutual nearest neighbors instead of closest pairs [Mamano et al.
    [Show full text]
  • On the Shape of Giant Soap Bubbles
    On the shape of giant soap bubbles Caroline Cohena,1, Baptiste Darbois Texiera,1, Etienne Reyssatb,2, Jacco H. Snoeijerc,d,e, David Quer´ e´ b, and Christophe Claneta aLaboratoire d’Hydrodynamique de l’X, UMR 7646 CNRS, Ecole´ Polytechnique, 91128 Palaiseau Cedex, France; bLaboratoire de Physique et Mecanique´ des Milieux Het´ erog´ enes` (PMMH), UMR 7636 du CNRS, ESPCI Paris/Paris Sciences et Lettres (PSL) Research University/Sorbonne Universites/Universit´ e´ Paris Diderot, 75005 Paris, France; cPhysics of Fluids Group, University of Twente, 7500 AE Enschede, The Netherlands; dMESA+ Institute for Nanotechnology, University of Twente, 7500 AE Enschede, The Netherlands; and eDepartment of Applied Physics, Eindhoven University of Technology, 5600 MB, Eindhoven, The Netherlands Edited by David A. Weitz, Harvard University, Cambridge, MA, and approved January 19, 2017 (received for review October 14, 2016) We study the effect of gravity on giant soap bubbles and show The experimental setup dedicated to the study of such large 2 that it becomes dominant above the critical size ` = a =e0, where bubbles is presented in Experimental Setup, before information p e0 is the mean thickness of the soap film and a = γb/ρg is the on Experimental Results and Model. The discussion on the asymp- capillary length (γb stands for vapor–liquid surface tension, and ρ totic shape and the analogy with inflated structures is presented stands for the liquid density). We first show experimentally that in Analogy with Inflatable Structures. large soap bubbles do not retain a spherical shape but flatten when increasing their size. A theoretical model is then developed Experimental Setup to account for this effect, predicting the shape based on mechan- The soap solution is prepared by mixing two volumes of Dreft© ical equilibrium.
    [Show full text]
  • Soap Films: Statics and Dynamics
    Soap Films: Statics and Dynamics Frederik Brasz January 8, 2010 1 Introduction Soap films and bubbles have long fascinated humans with their beauty. The study of soap films is believed to have started around the time of Leonardo da Vinci. Since then, research has proceeded in two distinct directions. On the one hand were the mathematicians, who were concerned with finding the shapes of these surfaces by minimizing their area, given some boundary. On the other hand, physical scientists were trying to understand the properties of soap films and bubbles, from the macroscopic behavior down to the molecular description. A crude way to categorize these two approaches is to call the mathematical shape- finding approach \statics" and the physical approach \dynamics", although there are certainly problems involving static soap films that require a physical description. This is my implication in this paper when I divide the discussion into statics and dynamics. In the statics section, the thickness of the film, concentration of surfactants, and gravity will all be quickly neglected, as the equilibrium shape of the surface becomes the only matter of importance. I will explain why for a soap film enclosing no volume, the mean curvature must everywhere be equal to zero, and why this is equivalent to the area of the film being minimized. For future reference, a minimal surface is defined as a two-dimensional surface with mean curvature equal to zero, so in general soap films take the shape of minimal surfaces. Carrying out the area minimization of a film using the Euler-Lagrange equation will result in a nonlinear partial differential equation known as Lagrange's Equation, which all minimal surfaces must satisfy.
    [Show full text]
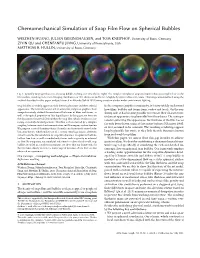
  • Chemomechanical Simulation of Soap Film Flow on Spherical Bubbles
    Chemomechanical Simulation of Soap Film Flow on Spherical Bubbles WEIZHEN HUANG, JULIAN ISERINGHAUSEN, and TOM KNEIPHOF, University of Bonn, Germany ZIYIN QU and CHENFANFU JIANG, University of Pennsylvania, USA MATTHIAS B. HULLIN, University of Bonn, Germany Fig. 1. Spatially varying iridescence of a soap bubble evolving over time (left to right). The complex interplay of soap and water induces a complex flowonthe film surface, resulting in an ever changing distribution of film thickness and hence a highly dynamic iridescent texture. This image was simulated using the method described in this paper, and path-traced in Mitsuba [Jakob 2010] using a custom shader under environment lighting. Soap bubbles are widely appreciated for their fragile nature and their colorful In the computer graphics community, it is now widely understood appearance. The natural sciences and, in extension, computer graphics, have how films, bubbles and foams form, evolve and break. On the ren- comprehensively studied the mechanical behavior of films and foams, as dering side, it has become possible to recreate their characteristic well as the optical properties of thin liquid layers. In this paper, we focus on iridescent appearance in physically based renderers. The main pa- the dynamics of material flow within the soap film, which results in fasci- rameter governing this appearance, the thickness of the film, has so nating, extremely detailed patterns. This flow is characterized by a complex far only been driven using ad-hoc noise textures [Glassner 2000], coupling between surfactant concentration and Marangoni surface tension. We propose a novel chemomechanical simulation framework rooted in lu- or was assumed to be constant.
    [Show full text]
  • Soap Bubbles for Volumetric Velocity Measurements in Air Flows
    13th International Symposium on Particle Image Velocimetry – ISPIV 2019 Munich, Germany, July 22-24, 2019 Soap bubbles for volumetric velocity measurements in air flows Diogo Barros1;2∗, Yanchong Duan4, Daniel Troolin3 Ellen K. Longmire1, Wing Lai3 1 University of Minnesota, Aerospace Engineering and Mechanics, Minneapolis, MN 55455, USA 2 Aix-Marseille Universite,´ CNRS, IUSTI, Marseille, France 3 TSI, Incorporated, 500 Cardigan Rd., Shoreview, MN, USA 4 State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China ∗ [email protected] Abstract The use of air-filled soap bubbles with diameter 10-30µm is demonstrated for volumetric velocimetry in air flows covering domains of 75-490cm3. The tracers are produced by a novel system that seeds high-density soap bubble streams for particle image velocimetry applications. Particle number density considerations, spatial resolution and response time scales are discussed in light of current seeding techniques for volumetric measurements. Finally, the micro soap bubbles are employed to measure the 3D velocity field in the wake of a sphere immersed in a turbulent boundary layer. 1 Introduction Volumetric velocimetry is a key enabler for understanding turbulent flows, which are inherently unsteady and three-dimensional. Multiple methods have been designed to measure 3D velocity fields accurately. In particular, particle image velocimetry (PIV) and particle tracking velocimetry (PTV) are now widely employed in various flow configurations (Discetti and Coletti, 2018). All of these techniques rely on imaging of discrete seeding tracers suspended in the flow. While larger seeding particles scatter more light from the illuminating source, smaller ones follow the flow more accurately and can resolve smaller scale variations.
    [Show full text]
  • THE GEOMETRY of BUBBLES and FOAMS University of Illinois Department of Mathematics Urbana, IL, USA 61801-2975 Abstract. We Consi
    THE GEOMETRY OF BUBBLES AND FOAMS JOHN M. SULLIVAN University of Illinois Department of Mathematics Urbana, IL, USA 61801-2975 Abstract. We consider mathematical models of bubbles, foams and froths, as collections of surfaces which minimize area under volume constraints. The resulting surfaces have constant mean curvature and an invariant notion of equilibrium forces. The possible singularities are described by Plateau's rules; this means that combinatorially a foam is dual to some triangulation of space. We examine certain restrictions on the combina- torics of triangulations and some useful ways to construct triangulations. Finally, we examine particular structures, like the family of tetrahedrally close-packed structures. These include the one used by Weaire and Phelan in their counterexample to the Kelvin conjecture, and they all seem useful for generating good equal-volume foams. 1. Introduction This survey records, and expands on, the material presented in the author's series of two lectures on \The Mathematics of Soap Films" at the NATO School on Foams (Cargese, May 1997). The first lecture discussed the dif- ferential geometry of constant mean curvature surfaces, while the second covered the combinatorics of foams. Soap films, bubble clusters, and foams and froths can be modeled math- ematically as collections of surfaces which minimize their surface area sub- ject to volume constraints. Each surface in such a solution has constant mean curvature, and is thus called a cmc surface. In Section 2 we examine a more general class of variational problems for surfaces, and then concen- trate on cmc surfaces. Section 3 describes the balancing of forces within a cmc surface.
    [Show full text]
  • Share Your Creations with Us on Social Media! Follow Us @Curriermuseum on Instagram and Follow Us on Facebook
    This is one image in a series of 12 by Terry Winters. The series, called Models for Synthetics Pictures, are prints and all consist of abstract compositions that share a web-like structure. By combining a variety of printmaking techniques, the artist has rendered the twelve images with richly textured black lines and colors of great intensity and variation. Winter draws inspiration from botanical anatomies, biological circulatory and nervous systems, color spectrums, architectural renderings and fractal geometry. Try making your own abstract and amorphic painting by making bubbles! ▪ Terry Winters, Levels, studied complexities, 1994, from Models for Synthetic Pictures, intaglio on Gampi paper laid down on Lana Gravure, 19 3/8 in. x 22 1/4 in. The Henry Melville Fuller Acquisition Fund Activity: Soap Bubble Printing - Create beautiful patterned paper using dish soap Materials: • Water • Acrylic or craft paint • Dish soap • Shallow pan or paper/plastic cups • Paintbrush, spoon, popsicle stick or another tool to stir • Straws (optional) • White paper Directions: • In a shallow pan, mix together one-part dish soap, one-part paint, and two-parts water • Stir until lots of bubbles appear on the surface of the water (if you don’t see many bubbles, try adding more soap) o You can also use a straw to blow into mixture which will make bubbles • Gently press your paper onto the top of the soap bubbles and see what designs transferred to your paper • Repeat with more colors and more pieces of paper as desired Tips: • Experiment with mixing different colors in the same pan of dish soap.
    [Show full text]
  • General Physics II Recitation Quiz 10 - Interference, Diffraction, Polarization Mar
    General Physics II Recitation Quiz 10 - Interference, Diffraction, Polarization Mar. 31, 2010 Name: For full credit, make your work clear. Show the formulas you use, all the essential steps, and results with correct units and correct number of significant figures. 1(3). Blue light (wavelength 400 nm) falls on a narrow slit that produces a diffraction pattern on a screen 5.0 m away. The width of the central maximum is 4 mm. How does this width change if a blue light is replaced with a red light (wavelength 700 nm). sin θBLUE = λBLUE=D ≈ xBLUE=L , where L = 5:0 m and xBLUE = 4:0 mm; For the red light we have sin θRED = λRED=D ≈ xRED=L Hence L=D ≈ xBLUE/λBLUE = xRED/λRED and xRED = 7:0 mm 2 (3). White unpolarized light passing through a Polaroid sheet is replaced with a plane-polarized light of the same intensity. It is known that the intensity of the light behind the Polaroid also remained the same. Determine the angle between the transmission axis of Polaroid and the original orientation of the plane- polarized light. 1 2 For unpolarized light I = 2 × I0 For polarized light I = I0 × cos θ 1 2 ◦ 2 = cos θ, hence θ = 45 3.(4) If a soap bubble is 120 nm thick, what wavelength is most strongly reflected at the center of the outer surface when illuminated by white light? The index of refraction in the soap bubble is 1.34 Let t = 120 nm and n = 1:34 The path difference between the wave reflected from the outer surface and the wave reflected from the inner surface is 2t.
    [Show full text]