On the Integration of Optimization and Agent Technology for Transportation and Production Planning
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Price Record Store Day 2019 Releases Price Follow Us on Twitter
Follow us on twitter @PiccadillyRecs for Follow us on twitter @PiccadillyRecs for Price ✓ Record Store Day 2019 Releases Price ✓ Price ✓ Record Store Day 2019 Releases Price ✓ updates on items selling out etc. updates on items selling out etc. 7" SINGLES 7" 14.99 Queen : Bohemian Rhapsody/I'm In Love With My Car 12" 22.99 John Grant : Remixes Are Also Magic 12" 9.99 Lonnie Liston Smith : Space Princess 7" 12.99 Anderson .Paak : Bubblin' 7" 13.99 Sharon Ridley : Where Did You Learn To Make Love The 12" Way You 11.99Do Hipnotic : Are You Lonely? 12" 10.99 Soul Mekanik : Go Upstairs/Echo Beach (feat. Isabelle Antena) 7" 16.99 Azymuth : Demos 1973-75: Castelo (Version 1)/Juntos Mais 7" Uma Vez9.99 Saint Etienne : Saturday Boy 12" 9.99 Honeyblood : The Third Degree/She's A Nightmare 12" 11.99 Spirit : Spirit - Original Mix/Zaf & Phil Asher Edit 7" 10.99 Bad Religion : My Sanity/Chaos From Within 7" 12.99 Shit Girlfriend : Dress Like Cher/Socks On The Beach 12" 13.99 Hot 8 Brass Band : Working Together E.P. 12" 9.99 Stalawa : In East Africa 7" 9.99 Erykah Badu & Jame Poyser : Tempted 7" 10.99 Smiles/Astronauts, etc : Just A Star 12" 9.99 Freddie Hubbard : Little Sunflower 12" 10.99 Joe Strummer : The Rockfield Studio Tracks 7" 6.99 Julien Baker : Red Door 7" 15.99 The Specials : 10 Commandments/You're Wondering Now 12" 15.99 iDKHOW : 1981 Extended Play EP 12" 19.99 Suicide : Dream Baby Dream 7" 6.99 Bang Bang Romeo : Cemetry/Creep 7" 10.99 Vivian Stanshall & Gargantuan Chums (John Entwistle & Keith12" Moon)14.99 : SuspicionIdles : Meat EP/Meta EP 10" 13.99 Supergrass : Pumping On Your Stereo/Mary 7" 12.99 Darrell Banks : Open The Door To Your Heart (Vocal & Instrumental) 7" 8.99 The Straight Arrows : Another Day In The City 10" 15.99 Japan : Life In Tokyo/Quiet Life 12" 17.99 Swervedriver : Reflections/Think I'm Gonna Feel Better 7" 8.99 Big Stick : Drag Racing 7" 10.99 Tindersticks : Willow (Feat. -

RSD19 Releases PRINTABLE 27.02.19
#RSD19 Twitter: @RSDUK / Instagram: @recordstoreday / Facebook: @RSDayUK Artist Title Label Format Want 13th Floor Elevators Psychedelic Sounds Of International Artists LP Picture Disc 808 State Four States of 808 ZTT 4x12" box set A Man Called Adam Farmarama Other Records Ltd. 12" A.R. Kane New Clear Child Hidden Art Recordings Single vinyl LP Ace Frehley Spaceman (Picture Disc) Eone Entertainment 12PD Ace of Base The Sign K7 7' PICTURE DISC Acid Mothers Temple Does The Cosmic Shepherd Space Age Recordings Double LP Dream Of Electric Tapirs? Adam French The Back Foot And Rapture Virgin EMI 7" A-HA Hunting High And Low / The Rhino 1LP, Black Vinyl Early Alternate Mixes Aidan Moffat and RM What The Night Bestows US Rock Action Records LP Hubbert Air Surfing On A Rocket Warner Music France 12" Picture Disc Airto Natural Feelings Real Gone Music 12" LP Al Green The Hi Records Singles Box Fat Possum Records 7" Box Set Set Alarm, The Live '85 Twenty First Century 2LP Recording Company Albert Washington Sad And Lonely Tidal Waves Music LP Alice Clark s/t Wewantsounds Deluxe Gatefold LP ALPHA & OMEGA DUBPLATE SELECTION VOL 1 MANIA DUB LP ALPHA & OMEGA DUBPLATE SELECTION VOL 2 MANIA DUB LP Anderson .Paak Bubblin' Aftermath/12 Tone 7" Music, LLC Andrea True More, More, More Buddah Records 12" Connection Angel Pavement Socialising With Angel Morgan Blue Town LP & 7" Pavement Antoine Dobson ft Bed Intruder & Various Enjoy The Ride 7" Gregory Bros Other YouTube Hits 1 #RSD19 Twitter: @RSDUK / Instagram: @recordstoreday / Facebook: @RSDayUK Apartments, -

20Th December 2017
20th December 2017 Dear Tytherington Families, Well done for another great term at Tytherington School. Particular congratulations go to the year 7 who have settled so well. As with all our Headteacher’s Notes, this edition is a snapshot of what we have been doing in school over the last fortnight. Below, I have included pictures of the wonderful Christmas House Pantomines which took place yesterday. We hope you enjoy this edition. If you would like to see other editions of Headteacher’s Notes, please visit: http:// www.tytheringtonschool.co.uk/category/news/headteacher/ In this fortnight’s edition: Year 11 Awards Evening Christmas Jumper Day Tytherington Dragons Take Team Prize Year 13 Awards Evening PE Update Chess Update A Level Literature Theatre Visit to London Christmas Poem Competition Year 11 Awards Evening by mr pepper On Thursday 16th December, students from our Year 11 cohort of 2017, parents, governors and staff packed into the main hall to enjoy a night of celebra- tion at Tytherington School’s annual Year 11 Awards Evening. Following thought-provoking speeches from our Headteacher Mr Botwe, Mr Pepper, Head of Year 11, and our Chair of Governors, Mrs Jane Stephens, stu- dents were cheered as they received their examina- tion certificates, before pastoral and academic awards were given out to recognise individual achievement. Three additional awards were also celebrated on the evening, including the “Wendy Pennington Prize for English”, the “Guy Wharton Award for Endeavour”, and our “Headteacher’s Award”. The Wendy Pennington Prize for English is presented in memory of Mrs Pennington who was Head of English at Tytherington School and a champion of the subject of English. -

Eco-Efficient Pavement Construction Materials
Eco-efficient Pavement Construction Materials This page intentionally left blank Woodhead Publishing Series in Civil and Structural Engineering Eco-efficient Pavement Construction Materials Edited by Fernando Pacheco-Torgal Serji Amirkhanian Hao Wang Erik Schlangen Woodhead Publishing is an imprint of Elsevier The Officers’ Mess Business Centre, Royston Road, Duxford, CB22 4QH, United Kingdom 50 Hampshire Street, 5th Floor, Cambridge, MA 02139, United States The Boulevard, Langford Lane, Kidlington, OX5 1GB, United Kingdom Copyright © 2020 Elsevier Ltd. All rights reserved. No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or any information storage and retrieval system, without permission in writing from the publisher. Details on how to seek permission, further information about the Publisher’s permissions policies and our arrangements with organizations such as the Copyright Clearance Center and the Copyright Licensing Agency, can be found at our website: www.elsevier.com/permissions. This book and the individual contributions contained in it are protected under copyright by the Publisher (other than as may be noted herein). Notices Knowledge and best practice in this field are constantly changing. As new research and experience broaden our understanding, changes in research methods, professional practices, or medical treatment may become necessary. Practitioners and researchers must always rely on their own experience and knowledge in evaluating and using any information, methods, compounds, or experiments described herein. In using such information or methods they should be mindful of their own safety and the safety of others, including parties for whom they have a professional responsibility. -

Toonzetters Tegendraadse Muziek Uit Een Nieuwe Werkplaats
Toonzetters Tegendraadse muziek uit een nieuwe werkplaats Listen to the silence, let it ring on Eyes, dark grey lenses frightened of the sun We would have a fine time living in the night, Left to blind destruction, Waiting for our sight Robert de Vaan 301111 DT4 KAL2 Toonzetters INHOUD (BLZ/HST/TITEL) 2 0. VOOR 3 1. JONGERENCULTUUR IN DE 20e EEUW:MASSA EN TEGENCULTUUR 4 2. PUNK 6 3. NEW WAVE 6 4. TONY WILSON 7 5 CLUBS 8 6. FACTORY RECORDS 9 7 JOY DIVISION 11 8. NEW ORDER 12 9. ACHTER 13 B1 BIJLAGE 1: ONAFHANKELIJKE LABELS IN DE JAREN 80 14 B2 BIJLAGE 2: FACTORY CATALOGUS 21 B3 BIJLAGE 3: BRONNNEN 0. VOOR Er bestaan in mijn optiek maar twee stromingen binnen de muziek, te weten goede en slechte. De goede is doorgaans authentiek en de gevoelens die Ian Curtis, frontman van Joy Division, bezong leken mij als tiener in de jaren 80 oprecht, hij had er niet voor niets een einde aan gemaakt. De muziek hoorde bij de stroming New Wave, waar ik actief onderdeel van werd . Generatie Nix, de naam die mijn generatie meekreeg, zou toch geen werk vinden en de atoomoorlog zou spoedig beginnen. I wear black on the outside because black is how I feel on the inside zei Morrisey en daar kan ik me tot op de dag van vandaag in vinden... In dit referaat ga ik op zoek naar mijn muzikale en sociale roots en naar de achtergronden van het verhaal van een bijzondere en alternatieve onderneming. New Wave, de stroming voor de subcultuur der alternatieven waarvan Ian Curtis pionier was, vond zijn oorsprong halverwege de jaren 70 in de tegendraadse Punk. -

Empire State Partnerships Project
EMPIRE STATE PARTNERSHIPS PROJECT FIVE YEAR EVALUATION SUMMARY REPORT CCT REPORTS NOVEMBER 2002 EMPIRE STATE PARTNERSHIPS PROJECT FIVE YEAR EVALUATION SUMMARY REPORT PREPARED BY TERRY BAKER BRONWYN BEVAN NOGA ADMON PEGGY CLEMENTS ANSLEY ERICKSON SARAH ADAMS EDUCATION DEVELOPMENT CENTER, INC. 96 Morton Street, 7th floor New York New York 10014 tel 212] 807.4200 fax 212] 633.8804 tty 212] 807.4284 web www.edc.org/CCT Copyright © 2004 by Education Development Center Inc. This report was written and produced by EDC’s Center for Children and Technology All rights reserved. No part of this report may be reproduced or transmitted in any form or by any means without permission in writing from the publisher, except where permitted by law. To inquire about permission, write to: ATTN: REPRINTS Center for Children and Technology 96 Morton Street, 7th Floor New York, NY 10017 Or email: [email protected] I TABLE OF CONTENTS BACKGROUND AND HISTORY . .2 EVALUATION METHODOLOGY . .9 ROLES AND LEADERSHIP . .10 PROJECT GOALS . .17 SITE EVALUATIONS . .20 BEST PRACTICES . .24 PARTNERSHIP . .26 ARTS-BASED CURRICULUM . .29 ASSESSMENT . .36 STANDARDS . .40 STUDENT IMPACT . .42 SCHOOL CHANGE . .44 TECHNOLOGY INTEGRATION . .51 PROFESSIONAL DEVELOPMENT . .56 SUMMER SEMINAR . .67 IMPLICATIONS . .95 1 n 1996, the Empire State Partnership program (ESP) was initiated as a collaboration between the New York State Council on the Arts (NYSCA) and the New York State Education Department (SED). This report chronicles the program from its origins through its initial five-year implementation phase. The report concludes with a synthesis of Iimpacts derived from the evaluation reports of the participating sites and from Education Development Center/Center for Children and Technology’s EDC/CCT evaluations, interviews, obser- vations, and survey data. -

13Th Floor Elevators Psychedelic Sounds of LP Picture Disc 24.99 808 State Four States of 808 4X12" Box Set 44.99 a Man Called Adam Farmarama 12" 11.99 A.R
Artist Title Format 13th Floor Elevators Psychedelic Sounds Of LP Picture Disc 24.99 808 State Four States of 808 4x12" box set 44.99 A Man Called Adam Farmarama 12" 11.99 A.R. Kane New Clear Child Single vinyl LP 21.99 Acid Mothers Temple Does The Cosmic Shepherd Dream Of Electric Tapirs? Double LP 25.99 A-HA Hunting High And Low / The Early Alternate Mixes 1LP, Black Vinyl 24.99 Aidan Moffat and RM Hubbert What The Night Bestows US LP 21.99 Air Surfing On A Rocket 12" Picture Disc 21.99 Airto Natural Feelings 12" LP 27.99 Al Green The Hi Records Singles Box Set 7" Box Set 114.99 Alarm, The Live '85 2LP 21.99 Albert Washington Sad And Lonely LP 29.99 Alice Clark s/t Deluxe Gatefold LP edition augmented39.99 with a 20 page booklet ALPHA & OMEGA DUBPLATE SELECTION VOL 1 LP 24.99 ALPHA & OMEGA DUBPLATE SELECTION VOL 2 LP 24.99 Anderson .Paak Bubblin' 7" 12.99 Angel Pavement Socialising With Angel Pavement LP & 7" Antoine Dobson featuring the Gregory Brothers (Schmoyo)Bed Intruder & Various Other YouTube Hits 7" 17.99 Aretha Franklin The Atlantic Singles Collection 1967 5 x 7" Singles Box 69.99 Art Brut X We Are Scientists WASABI 12" LP 16.99 Art of Noise Daft As A Brush! 4x12" box set 44.99 Associates Club Country 12" - coloured vinyl 18.99 Bad Religion My Sanity/Chaos From Within 7" 11.99 Bananarama DRAMA: LIMITED EDITION COLOURED VINYL DOUBLE LP LP Bananarama VIVA: LIMITED EDITION COLOURED VINYL DOUBLE LP LP Bananarama Bananarama Remixed: Vol. -

RSD 2019 List 2.Xlsx
Spinning Discs Sheffield - RSD 2019 Stock List Releases ordered in for RSD19 Artist Title Price 13TH FLOOR ELEVATORS PSYCHEDELIC SOUNDS (RSD) £ 22.99 808 State Four States of 808 £ 43.99 A-HA Hunting High And Low / The Early Alternate Mixes £ 23.99 Ace of Base The Sign £ 13.99 Acid Mothers Temple Does The Cosmic Shepherd Dream Of Electric Tapirs? £ 26.99 Aidan Moffat & RM Hubbert What The Night Bestows Us £ 22.99 Air Surfing On A Rocket £ 20.99 Al Green The Hi Records Singles Collection Box Set £ 125.99 ALARM,THE LIVE ‘85 (RSD 2019) £ 21.99 Alice Clark Alice Clark £ 41.99 Anderson Paak Bubblin' £ 12.99 Angelo Badalamenti and David Lynch Twin Peaks: Season Two Music And More £ 31.99 Aretha Franklin The Atlantic Singles Collection 1967 £ 67.99 ART BRUT X WE ARE SCIENTISTS WASABI £ 16.99 Art of Noise Daft As A Brush! £ 43.99 Average White Band Pick Up The Pieces / Get it up fot Love £ 10.99 BADU,ERYKAH & JAMES POYSER TEMPTED (RSD 2019) £ 9.99 Bananarama DRAMA: LIMITED EDITION COLOURED VINYL DOUBLE LP £ 35.99 Bananarama VIVA: LIMITED EDITION COLOURED VINYL DOUBLE LP £ 35.99 Bananarama Bananarama Remixed: Vol. 1 £ 12.99 BARNETT,COURTNEY EVERYBODY HERE HATES YOU £ 11.99 Basil Kirchin Worlds Within Worlds (Part I and II) £ 26.99 Bastille Other Peoples Heartache £ 22.99 Bernard Pretty Purdie Soul Is Pretty Purdie £ 33.99 Billy Joel Live At Carnegie Hall 1977 £ 27.99 Bingo Hand Job Live At The Borderline 1991 £ 28.99 Blossoms Cool Like You £ 26.99 Bob Dylan Blood On The Tracks - Original New York Test Pressing £ 23.99 Boy George & Culture Club Runaway Train (ft. -

COB RECORDS 1/2/3 Britannia Terrace, Porthmadog, Gwynedd, Wales, U.K
COB RECORDS 1/2/3 Britannia Terrace, Porthmadog, Gwynedd, Wales, U.K. LL49 9NA. Tel: 01766 – 512170. Fax: 01766 – 513185 w.w.w. cobrecords.com e-mail: [email protected] Retail & World-Wide Mail Order Specialists (Established 1967) Mail-Order Master Catalogue of Top Selling CDs 1997 - 2000 Over the past four years covered by this catalogue some 65,000 titles were released – we list here some 5,500 of our Top Sellers. If the titles you require are not listed, please contact us; as we deal with all the major U.K. manufacturers and distributors as well as Overseas sources, we should be able to supply most available items. All items are coded (A1, B3, C8 etc) as well as priced; in the event of any price increases we will advise you before-hand of these by amending the codes to price formula. You can order either by e-mail or use the on-line order form or you can use our Yellow Order forms for posting orders in. Alternatively, you can ‘phone your orders through. We have tried avoiding listing any deletions but unfortunately with the quantity involved it is inevitable some titles may have recently been deleted. Please check our separate Top Selling CDs At Special Discount Prices listing – you will find some titles listed at cheaper prices. We have secured a deal which enables us to supply selective CDs at very attractive prices – long may it last. Our Retail Outlet carries a vast selection of both New & Quality Guaranteed Second Hand CDs, LPs, Tapes, Videos & DVDs – we always have in stock 15,000+ titles to suit all tastes. -
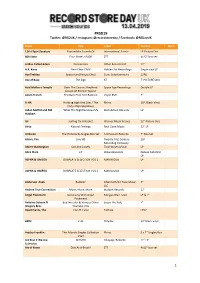
RSD19 Twitter: @RSDUK / Instagram: @Recordstoreday / Facebook: @Rsdayuk
#RSD19 Twitter: @RSDUK / Instagram: @recordstoreday / Facebook: @RSDayUK Artist Title Label Format Want 13th Floor Elevators Psychedelic Sounds Of International Artists LP Picture Disc 808 State Four States of 808 ZTT 4x12" Box set A Man Called Adam Farmarama Other Records Ltd. 12" A.R. Kane New Clear Child Hidden Art Recordings Single vinyl LP Ace Frehley Spaceman (Picture Disc) Eone Entertainment 12PD Ace of Base The Sign K7 7' PICTURE DISC Acid Mothers Temple Does The Cosmic Shepherd Space Age Recordings DouBle LP Dream Of Electric Tapirs? Adam French The Back Foot And Rapture Virgin EMI 7" A-HA Hunting High And Low / The Rhino 1LP, Black Vinyl Early Alternate Mixes Aidan Moffat and RM What The Night Bestows US Rock Action Records LP Hubbert Air Surfing On A Rocket Warner Music France 12" Picture Disc Airto Natural Feelings Real Gone Music 12" LP Al Green The Hi Records Singles Box Set Fat Possum Records 7" Box Set Alarm, The Live '85 Twenty First Century 2LP Recording Company Albert Washington Sad And Lonely Tidal Waves Music LP Alice Clark s/t Wewantsounds Deluxe Gatefold LP ALPHA & OMEGA DUBPLATE SELECTION VOL 1 MANIA DUB LP ALPHA & OMEGA DUBPLATE SELECTION VOL 2 MANIA DUB LP Anderson .Paak Bubblin' Aftermath/12 Tone Music, 7" LLC Andrea True Connection More, More, More Buddah Records 12" Angel Pavement Socialising With Angel Morgan Blue Town LP & 7" Pavement Antoine Dobson ft Bed Intruder & Various Other Enjoy The Ride 7" Gregory Bros YouTuBe Hits Apartments, The Live At L'uBu Talitres LPX2 APRE 2.45 Polydor 12" Black vinyl Aretha -

RSD 2019 Update 12042019
Spinning Discs Sheffield - RSD 2019 Stock List Version 4 - as of Friday 12th April 2019 Releases in for RSD19 Artist Title Format Price 13TH FLOOR ELEVATORS PSYCHEDELIC SOUNDS (RSD) LP £ 22.99 808 State Four States of 808 4x12" box set £ 43.99 A-HA Hunting High And Low / The Early Alternate Mixes 1LP, Black Vinyl £ 23.99 Acid Mothers Temple Does The Cosmic Shepherd Dream Of Electric Tapirs? 2 £ 26.99 Aidan Moffat & RM Hubbert What The Night Bestows Us LP £ 22.99 Air Surfing On A Rocket 12" Picture Disc £ 20.99 Al Green The Hi Records Singles Collection Box Set 26 x 7" Single Boxset £ 105.99 ALARM,THE LIVE ‘85 (RSD 2019) LP £ 21.99 Alice Clark Alice Clark LP £ 41.99 Anderson Paak Bubblin' 7" £ 12.99 Angelo Badalamenti and David Lynch Twin Peaks: Season Two Music And More 2-LP – 180g colour vinyl w/ gatefold jacket £ 31.99 Aretha Franklin The Atlantic Singles Collection 1967 5 x 7" Singles Box £ 67.99 ART BRUT X WE ARE SCIENTISTS WASABI LP £ 16.99 Art of Noise Daft As A Brush! 4x12" box set £ 43.99 Average White Band Pick Up The Pieces / Get it up fot Love 12" £ 10.99 BADU,ERYKAH & jAMES POYSER TEMPTED (RSD 2019) 7 £ 9.99 Bananarama DRAMA: LIMITED EDITION COLOURED VINYL DOUBLE LP 2LP £ 35.99 Bananarama VIVA: LIMITED EDITION COLOURED VINYL DOUBLE LP 2LP £ 35.99 Bananarama Bananarama Remixed: Vol. 1 12" EP £ 12.99 BARNETT,COURTNEY EVERYBODY HERE HATES YOU 12 £ 11.99 Basil Kirchin Worlds Within Worlds (Part I and II) LP £ 26.99 Bastille Other Peoples Heartache 12Ó £ 22.99 Bernard Pretty Purdie Soul Is Pretty Purdie LP £ 33.99 Billy Joel Live At Carnegie Hall 1977 x2 LP Vinyl £ 27.99 Bingo Hand job Live At The Borderline 1991 2LP £ 28.99 Blossoms Cool Like You LP Set £ 26.99 Bob Dylan Blood On The Tracks - Original New York Test Pressing LP Vinyl £ 23.99 Boy George & Culture Club Runaway Train (ft.