Copyrighted Material
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Principle of Pharmacodynamics
Principle of pharmacodynamics Dr. M. Emamghoreishi Full Professor Department of Pharmacology Medical School Shiraz University of Medical Sciences Email:[email protected] Reference: Basic & Clinical Pharmacology: Bertrum G. Katzung and Anthony J. Treveror, 13th edition, 2015, chapter 20, p. 336-351 Learning Objectives: At the end of sessions, students should be able to: 1. Define pharmacology and explain its importance for a clinician. 2. Define ―drug receptor‖. 3. Explain the nature of drug receptors. 4. Describe other sites of drug actions. 5. Explain the drug-receptor interaction. 6. Define the terms ―affinity‖, ―intrinsic activity‖ and ―Kd‖. 7. Explain the terms ―agonist‖ and ―antagonist‖ and their different types. 8. Explain chemical and physiological antagonists. 9. Explain the differences in drug responsiveness. 10. Explain tolerance, tachyphylaxis, and overshoot. 11. Define different dose-response curves. 12. Explain the information that can be obtained from a graded dose-response curve. 13. Describe the potency and efficacy of drugs. 14. Explain shift of dose-response curves in the presence of competitive and irreversible antagonists and its importance in clinical application of antagonists. 15. Explain the information that can be obtained from a quantal dose-response curve. 16. Define the terms ED50, TD50, LD50, therapeutic index and certain safety factor. What is Pharmacology?It is defined as the study of drugs (substances used to prevent, diagnose, and treat disease). Pharmacology is the science that deals with the interactions betweena drug and the bodyor living systems. The interactions between a drug and the body are conveniently divided into two classes. The actions of the drug on the body are termed pharmacodynamicprocesses.These properties determine the group in which the drug is classified, and they play the major role in deciding whether that group is appropriate therapy for a particular symptom or disease. -

Prof. Hanan Hagar Quantitative Aspects of Drugs
Quantitative aspects of drugs Prof. hanan Hagar Ilos Determine quantitative aspects of drug receptor binding. Recognize concentration binding curves. Identify dose response curves and the therapeutic utility of these curves. Classify different types of antagonism QUANTIFY ASPECTS OF DRUG ACTION Bind Initiate Occupy Activate D + R D R DR* RESPONSE[R] Relate concentration [C] of D used (x- axis) Relate concentration [C] of D used (x- to the binding capacity at receptors (y-axis) axis) to response produced (y-axis) Concentration-Binding Curve Dose Response Curves AFFINITY EFFICACY POTENCY Concentration binding curves Is a correlation between drug concentration [C] used (x- axis) and drug binding capacity at receptors [B] (y-axis). i.e. relation between concentration & drug binding Concentration-Binding curves are used to determine: oBmax (the binding capacity) is the total density of receptors in the tissues. oKD50 is the concentration of drug required to occupy 50% of receptors at equilibrium. oThe affinity of drug for receptor The higher the affinity of D for receptor the lower is the KD i.e. inverse relation Concentration-Binding Curve (Bmax): Total density of receptors in the tissue K D KD (kD )= [C] of D required to occupy 50% of receptors at equilibrium Dose -response curves o Used to study how response varies with the concentration or dose. o Is a correlation between drug concentration [D] used (x- axis) and drug response [R] (y-axis). o i.e. relation between concentration & Response TYPES of Dose -response curves Graded dose-response curve Quantal dose-response curve (all or none). Graded Dose-response Curve o Response is gradual o Gradual increase in response by increasing the dose (continuous response). -

Factors Affecting Drug Response2
Types of drug concentration– response relationship A. Graded drug concentration-Response Relationships As the dose of a drug is increased, the response (effect) of the tissue or organ is also increased. The efficacy (Emax) and potency (ED50) parameters are derived from these data. 112 GRADED DOSE- RESPONSE CURVE QUANTAL DOSE- RESPONSE CURVE 113 B. Quantal or all or none dose response relation ship. The Plot of the fraction of the population that responds at each dose of the drug versus the log of the dose administered. responses follow all or none phenomenon – that means the individual of the responding system either respond to their maximum limit or not at all to a dose of drug and there is no gradation of response. population studies. relates dose to frequency of effect . The median effective (ED50), median toxic (TD50) ,and median lethal doses (LD50) are extracted from experiments carried out in this manner. 114 Median effective dose (ED50):the dose at which 50% of individuals exhibit the specified quantal effect. Median toxic dose (TD50) :the dose required to produce a particular toxic effect in 50% of animals. Median lethal dose (LD50): is the lethal dose that causes death in 50% animal under experiment. 115 119 1. Excretion - Alteration of urine PH. e.g. Phanobarbitone + NaHCo3 - Alteration of active tubular secretion e.g. Probenecid + peincillin. II – Pharmcodynamic interaction - It occurs by modification of pharmacological response of one drug by another without altering the concentration of the drug in the tissue or tissue fluid. 1. Additive – Occurs when the combined effect of two drugs is equal to the sum of the effects of each agent given alone. -

PHARMACOLOGY the HISTORY of PHARMACOLOGY Prehistoric People Recognized the Beneficial Or Toxic Effects of Many Plant and Animal Materials
Lecture 1_2 Dr.Labeeb PHARMACOLOGY THE HISTORY OF PHARMACOLOGY Prehistoric people recognized the beneficial or toxic effects of many plant and animal materials. Early written records from Iraq, China and from Egypt list remedies of many types, including a few still recognized as useful drugs today. Most, however, were worthless or actually harmful . In the 1500 years ago introduced rational methods into medicine, but none was successful owing to the dominance of systems of thought that purported to explain all of biology and disease without the need for experimentation and observation, This idea that disease was caused by excesses of bile or blood in the body, that wounds could be healed by applying a salve to the weapon that caused the wound, and so on. Around the end of the 17th century, reliance on observation and experimentation began to replace theorizing in medicine. As the value of these methods in the study of disease became clear, physicians began to apply them to the effects of traditional drugs used in their own practices. In the late 18th and early 19th centuries, began to develop the methods of experimental animal physiology and pharmacology. Advances in chemistry and the further development of physiology therapeutics only about 50 years ago it become possible to accurately evaluate therapeutic claims. Around the same time, a major expansion of research efforts in all areas of biology began. As new concepts and new techniques were introduced, information accumulated about drug action. Two general principles that the student should always remember are, first, that all substances can under certain circumstances be toxic; and second, that all dietary supplements and all therapies promoted as health-enhancing should meet the same standards of efficacy and safety,. -

Estimation of Nizatidine Gastric Nitrosatability and Product Toxicity Via an Integrated Approach Combining HILIC, in Silico Toxicology, and Molecular Docking
journal of food and drug analysis 27 (2019) 915e925 Available online at www.sciencedirect.com ScienceDirect journal homepage: www.jfda-online.com Original Article Estimation of nizatidine gastric nitrosatability and product toxicity via an integrated approach combining HILIC, in silico toxicology, and molecular docking * ** Rania El-Shaheny a,b, , Mohamed Radwan c,d,e, Koji Yamada f, , Mahmoud El-Maghrabey a,g a Department of Pharmaceutical Analytical Chemistry, Faculty of Pharmacy, Mansoura University, Mansoura 35516, Egypt b Department of Hygienic Chemistry and Toxicology, Course of Pharmaceutical Sciences, Graduate School of Biomedical Sciences, Nagasaki University, 1-14 Bunkyo-machi, Nagasaki 852-8521, Japan c Department of Drug Discovery, Science Farm Ltd., 1-7-30 Kuhonji, Chuo-ku, Kumamoto 862-0976, Japan d Department of Bioorganic Medicinal Chemistry, Faculty of Life Sciences, Kumamoto University, 5e1 Oehonmachi, Chuo-ku, Kumamoto 862e0973, Japan e Chemistry of Natural Compounds Department, Pharmaceutical and Drug Industries Research Division, National Research Centre, Dokki 12622, Cairo, Egypt f Medical Plant Laboratory, Course of Pharmaceutical Sciences, Graduate School of Biomedical Sciences, Nagasaki University, 1-14 Bunkyo-machi, Nagasaki 852-8521, Japan g Department of Analytical Chemistry for Pharmaceuticals, Course of Pharmaceutical Sciences, Graduate School of Biomedical Sciences, Nagasaki University, 1-14 Bunkyo-machi, Nagasaki 852-8521, Japan article info abstract Article history: The liability of the H2-receptor antagonist nizatidine (NZ) to nitrosation in simulated Received 24 June 2019 gastric juice (SGJ) and under WHO-suggested conditions was investigated for the first time. Received in revised form For monitoring the nitrosatability of NZ, a hydrophilic interaction liquid chromatography 29 July 2019 (HILIC) method was optimized and validated according to FDA guidance. -

Provisional Peer Reviewed Toxicity Values for 4-Amino-2,6-Dinitrotoluene
EPA/690/R-20/002F | June 2020 | FINAL Provisional Peer-Reviewed Toxicity Values for 4-Amino-2,6-dinitrotoluene (CASRN 19406-51-0) U.S. EPA Office of Research and Development Center for Public Health and Environmental Assessment EPA/690/R-20/002F June 2020 https://www.epa.gov/pprtv Provisional Peer-Reviewed Toxicity Values for 4-Amino-2,6-dinitrotoluene (CASRN 19406-51-0) Center for Public Health and Environmental Assessment Office of Research and Development U.S. Environmental Protection Agency Cincinnati, OH 45268 ii 4-Amino-2,6-dinitrotoluene AUTHORS, CONTRIBUTORS, AND REVIEWERS CHEMICAL MANAGER Daniel D. Petersen, MS, PhD, DABT, ATS, ERT Center for Public Health and Environmental Assessment, Cincinnati, OH DRAFT DOCUMENT PREPARED BY SRC, Inc. 7502 Round Pond Road North Syracuse, NY 13212 PRIMARY INTERNAL REVIEWERS Jeffry L. Dean II, PhD Center for Public Health and Environmental Assessment, Cincinnati, OH Michelle M. Angrish, PhD Center for Public Health and Environmental Assessment, Research Triangle Park, NC This document was externally peer reviewed under contract to Eastern Research Group, Inc. 110 Hartwell Avenue Lexington, MA 02421-3136 Questions regarding the content of this PPRTV assessment should be directed to the U.S. EPA Office of Research and Development’s Center for Public Health and Environmental Assessment. iii 4-Amino-2,6-dinitrotoluene TABLE OF CONTENTS COMMONLY USED ABBREVIATIONS AND ACRONYMS ................................................... v BACKGROUND ........................................................................................................................... -

Mechanism of Drug Action
Compiled and circulated by Dr. Parimal Dua, Assistant Professor, Dept. of Physiology, Narajole Raj college Unit IV: Pharmacodynamics: Concept of LD50, LC50, TD50 and therapeutic index Quantal dose-response graphs can be characterised by the median effective dose (ED50). The median effective dose is the dose at which 50% of individuals exhibit the specified quantal effect. The median toxic dose is the dose required to produce a defined toxic effect in 50% of subjects. The median lethal dose is the dose required to kill 50% of subjects. The therapeutic index is the ratio of the TD50 to the ED50, a parameter which reflects the selectivity of a drug to elicit a desired effect rather than toxicity. The therapeutic window is the range between the minimum toxic dose and the minimum therapeutic dose, or the range of doses over which the drug is effective for most of the popuation and the toxicity is accceptable. Anatomy of the quantal dose-response graph contain the following elements: Three sigmoid curves The median effective dose (ED50) The median toxic dose (TD50) The median lethal dose (LD50) The therapeutic window The end result should look something like this: Page | 1 SEC-4: Pharmacology and Toxicology Compiled and circulated by Dr. Parimal Dua, Assistant Professor, Dept. of Physiology, Narajole Raj college Median effective dose, ED50 This thing is distinct from the identical ED50 in graded dose-response curves, where it corresponds to a measure of the potency of a drug, being the dose of a drug required to produce 50% of that drug’s maximal effect. -
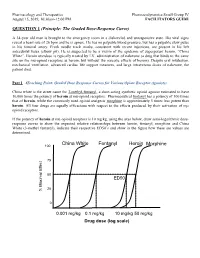
QUESTION 1 (Principle: the Graded Dose-Response Curve)
Pharmacology and Therapeutics Pharmacodynamics Small Group IV August 15, 2019, 10:30am-12:00 PM FACILITATORS GUIDE QUESTION 1 (Principle: The Graded Dose-Response Curve) A 34-year old man is brought to the emergency room in a disheveled and unresponsive state. His vital signs reveal a heart rate of 26 bpm and he is apneic. He has no palpable blood pressure, but has a palpable slow pulse in his femoral artery. Fresh needle track marks, consistent with recent injections, are present in his left antecubital fossa (elbow pit). He is suspected to be a victim of the epidemic of superpotent heroin, “China White”. Heroin overdose is typically treated by I.V. administration of naloxone (a drug that binds to the same site on the mu-opioid receptors as heroin, but without the narcotic effects of heroin). Despite oral intubation, mechanical ventilation, advanced cardiac life support measures, and large intravenous doses of naloxone, the patient died. Part 1 (Teaching Point: Graded Dose Response Curves for Various Opiate Receptor Agonists) China white is the street name for 3-methyl-fentanyl, a short-acting synthetic opioid agonist estimated to have 10,000 times the potency of heroin at mu-opioid receptors. Pharmaceutical fentanyl has a potency of 100 times that of heroin, while the commonly used opioid analgesic morphine is approximately 5 times less potent than heroin. All four drugs are equally efficacious with respect to the effects produced by their activation of m opioid receptors. If the potency of heroin at mu-opioid receptors is 10 mg/kg, using the axes below, draw semi-logarithmic dose- response curves to show the expected relative relationships between heroin, fentanyl, morphine and China White (3-methyl fentanyl), indicate their respective ED50’s and show in the figure how these are values are determined. -
![7. Calculation of Doses- General Considerations.Ppt [相容模式]](https://docslib.b-cdn.net/cover/5360/7-calculation-of-doses-general-considerations-ppt-2275360.webp)
7. Calculation of Doses- General Considerations.Ppt [相容模式]
Calculation of Doses: General considerations 劑量計算:一般考量 Objectives 1 Dose definitions n The dose of a drug: q is the quantitative amount administered or taken by a patient for the intended medicinal effect. q may be expressed as: n a single dose, the amount taken at one time; n a daily dose; n a total dose, the amount taken during the time-course of therapy. n A daily dose: q may be subdivided and taken in divided doses, q two or more times per day depending on the characteristics of the drug and the illness. n The schedule of dosing {e.g., four times per day for 10 days) is referred to as the dosage regimen. 2 n Drug dosesvary greatly between drug substances; some drugs have small doses, other drugs have relatively large doses. n The dose of a drug is based on: q its biochemical and pharmacologic activity, q its physical and chemical properties, q the dosage form used, q the route of administration, q various patient factors. n The dose of a drug for a particular patient may be determined in part on the basis of the patient's age, weight, body surface area, general physical health, liver and kidney function (for drug metabolism and elimination), and the severity of the illness being treated. n The usual adult dose of a drug is the amount that ordinarily produces the medicinal effect intended in adults. n The usual pediatric dose is similarly defined for the infant-or child-patient. n The usual dosage range for a drug indicates the quantitative range or amounts of the drug that may be prescribed within the guidelines of usual medical practice. -

1 Pharmacology Week 1 – General
Pharmacology week 1 – General Pharmacodynamics - actions of the drug on the body Receptors - component of cell/ organism that interact with drug and initiates chain of biochemical events leading to effects Dose response - Relationship between drug concentration and effect – in vitro Antagonist - drug which binds to a receptor but does not activate it, preventing agonists from binding Pharmacological antagonist - binds to a receptor without activating it Physiological antagonist - counters effects of another by binding to different receptor causing opposing effects eg insulin decreases glucose with steroids Chemical antagonist - counters effects of another by binding drug and blocking action eg protamine and heparin Competitive antagonist - In presence of fixed agonist conc, increasing concs of competitive antagonists progressively inhibit agonist response and vice versa . Bind reversibly, parallel shift of log dose/effect curve Irreversible antagonist - Pharmacologic antagonist that cannot be overcome by increasing dose of agonist Agonist - drug which binds to and activates a receptor which directly or indirectly brings about an effect Full agonist or Partial agonist - produce lower than max response at full occupancy eg pindolol, buprenorphine (full agonist plus partial agonist half way in between) Spare receptors - If a given conc of agonist causes maximal effect without binding to all receptors effect Log conc A–agonist; B–agonist+low dose antag; C–agonist uses all spare receptors; D,E–high conc antag diminish submax response Dose-response -

Evaluation of Anticonvulsant Activity of QUAN-0806 in Various Murine Experimental Seizure Models
ORIGINAL ARTICLES Key Laboratory of Organism Functional Factors of the Changbai Mountain (Yanbian University)1, Ministry of Education, Yanji; College of Pharmacy2, Yanbian University, Yanji; College of Medicine3, Jilin, P.R. China Evaluation of anticonvulsant activity of QUAN-0806 in various murine experimental seizure models Li-Ping Guan1,2, Dong-Hai Zhao3, Zhe Jiang2, Hu-Ri Piao2, Zhe-Shan Quan1,2 Received September 9, 2008, accepted October 10, 2008 Zhe-Shan Quan, College of Pharmacy, Yanbian University, No. 121, JuZi Street, Yanji City, Jilin Pro- vince, P.R. China [email protected] Pharmazie 64: 248–251 (2009) doi: 10.1691/ph.2009.8738 A new quinoline derivative, QUAN-0806 (7-hexyloxy-5-phenyl-1,2,4-triazolo[4,3-a]quinoline) was tested for anticonvulsant activity using the maximal electroshock seizure (MES) and the rotarod neurotoxicity (Tox) tests in mice. The MES test showed that QUAN-0806 exhibited higher activity (ED50 ¼ 6.5 mg/kg) and lower toxicity (TD50 ¼ 228.2 mg/kg), resulting in a higher protective index (PI ¼ 35.1) than the reference drugs phenytoin, carbamazepin, phenobarbital, and valproate. In addition, QUAN-0806 was found to exhibit significant oral activity against MES-induced seizures with low oral neurotoxicity in mice. QUAN-0806 was tested in chemically induced models (pentylenetetrazole, PTZ; isoniazid, ISO; 3-mercaptopropionic acid, 3-MPA; and strychnine, STRYC) to further investigate the anticonvulsant activity. QUAN-0806 produced significant antagonistic activity against seizures induced by PTZ, 3-MPA, and ISO, suggesting that QUAN-0806 influences GABAergic neurotransmission by activating gluta- mate decarboxylase (GAD) or inhibiting (GABA)-a-oxoglutarate aminotransferase (GABA-T) in the brain. -

Module I BASIC PRINCIPLES of PHARMACOLOGY 1) the Nature of Drugs
Module I BASIC PRINCIPLES OF PHARMACOLOGY 1) The nature of drugs. 2) Characteristic (or properties) of drug molecule. 3) Drug reactivity and drug-receptor bonds. 4) Controlled clinical trial. 5) Definition and uses of pharmacokinetics. 6) Ways and means of the introduction medicine (routes of administration). 7) The absorption (permeation): mechanisms. Drug absorption from the intes- tine, factors affecting gastrointestinal absorption. 8) Transport medicinal material. 9) Pharmacologic role of the P-glycoprotein /permeability glycoprotein/ (multi- drug-resistance type 1 transporter). 10) Bioavailability and bioequivalence. 11) The effect (presystemic metabolism) of first-pass hepatic elimination: ex- traction ratio and the first-pass effect, alternative routes of administration and the first-pass effect. 12) Prodrugs: definition, pharmacological means, classification (types and subtypes), examples. 13) Distribution of the drugs (volume of distribution). 14) Drug clearance principles: the ways of the elemination medicine from or- ganism. 15) Half-life period (t1/2) (probabilistic nature of half-life, formulae for half- life in exponential decay, half-life in non-exponential decay), pharmacologic role. 16) Drug accumulation (tapes; accumulation factors). 17) Mathematical modeling of the pharmacokinetic processes (single- compartment pharmacokinetic model, two-compartment model). 18) Metabolism of the drugs (drug biotransformation). The role of biotrans- formation in drug disposition. 19) Human liver P450 enzymes and cytochrome P450 cycle