PDE-Based Image Compression Based on Edges and Optimal Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

JPEG File Interchange Format Version 1.02
JPEG File Interchange Format Version 1.02 September 1, 1992 Eric Hamilton C-Cube Microsystems 1778 McCarthy Blvd. Milpitas, CA 95035 +1 408 944-6300 Fax: +1 408 944-6314 E-mail: [email protected] JPEG File Interchange Format Version 1.02 Why a File Interchange Format JPEG File Interchange Format is a minimal file format which enables JPEG bitstreams to be exchanged between a wide variety of platforms and applications. This minimal format does not include any of the advanced features found in the TIFF JPEG specification or any application specific file format. Nor should it, for the only purpose of this simplified format is to allow the exchange of JPEG compressed images. JPEG File Interchange Format features • Uses JPEG compression • Uses JPEG interchange format compressed image representation • PC or Mac or Unix workstation compatible • Standard color space: one or three components. For three components, YCbCr (CCIR 601-256 levels) • APP0 marker used to specify Units, X pixel density, Y pixel density, thumbnail • APP0 marker also used to specify JFIF extensions • APP0 marker also used to specify application-specific information JPEG Compression Although any JPEG process is supported by the syntax of the JPEG File Interchange Format (JFIF) it is strongly recommended that the JPEG baseline process be used for the purposes of file interchange. This ensures maximum compatibility with all applications supporting JPEG. JFIF conforms to the JPEG Draft International Standard (ISO DIS 10918-1). The JPEG File Interchange Format is entirely compatible with the standard JPEG interchange format; the only additional requirement is the mandatory presence of the APP0 marker right after the SOI marker. -

A Future Projection of Hardware, Software, and Market Trends of Tablet Computers
A Future Projection of Hardware, Software, and Market Trends of Tablet computers Honors Project In fulfillment of the Requirements for The Esther G. Maynor Honors College University of North Carolina at Pembroke By Christopher R. Hudson Department of Mathematics and Computer Science April 15,2013 Name Date Honors CoUege Scholar Name Date Faculty Mentor Mark Nfalewicz,/h.D. / /" Date Dean/Esther G/Maynor Honors College Acknowledgments We are grateful to the University of North Carolina Pembroke Department of Computer Science for the support of this research. We are also grateful for assistance with editing by Jordan Smink. ii TABLE OF CONTENTS Abstract........................................................................................................................................... 1 Background..................................................................................................................................... 2 Materials and Methods.................................................................................................................... 3 Results……..................................................................................................................................... 5 Discussion...................................................................................................................................... 8 References..................................................................................................................................... 10 iii List of Tables Table 1 Page 7 -

Bestpractice
The Innovative Instructor BestForum Practice Center for September 2010 c Educational e r Resources Image Resolution Reid Sczerba, Multimedia Developer, CER What it is What this is Image resolution is a concept that always The Innovative Instructor is a forum comes up when working with digital images. that publishes articles related to The resolution of an image has implications teaching excellence at Johns Hopkins for the final output of the image, whether that output is a printed poster or an image on a website. An understanding of image About the CER resolution ensures that the end result is The Center for Educational Resources clear, crisp, and of an appropriate file size. partners with faculty and graduate students to extend instructional impact by connecting innovative Why it matters How to do it teaching strategies and instructional Choosing a resolution that is too low will The term, “resolution,” refers to the num- technologies produce images that appear blurry or fuzzy ber of visual elements found within a phys- when printing. Printed products that are ical unit of measure. Every image, digital or For information on blurry will appear unprofessional, reducing not, is made up of tiny elements of color. how to contribute to their effectiveness. Understanding screen For print media, these elements are the The Innovative Instructor or resolution is also essential when sizing grains in photographic film or the colored to access archived articles, images for both websites and PowerPoint dots in a magazine. The same is true for presentations to ensure a fast load time. digital images: they are made up of an ar- please visit our website Fortunately, these complications can be ray of colored square pixels, like tiles in a • www.cer.jhu.edu/ii accommodated if resolution is considered mosaic. -

JHC DIGITAL ART December 20, 2011
JHC DIGITAL ART December 20, 2011 JHC - Digital Art Checklist GENERAL Figures intended for color are saved in RGB Figures intended for grayscale or black and white are saved in Grayscale format Figures and panels intended as single composites are supplied as a single file Sizing Figures are no wider than 6.75” (17.1 cm) and no taller than 8.75” (22.2 cm) Layout Spacing (routing) between panels in each figure is uniform, ~1-2mm wide, and white in color Figures are laid out in Portrait (8.5 x 11) orientation Labeling Figures have been numbered sequentially in Arabic numerals (1, 2, 3, etc.) Figure panels have been labeled in upper-case letters only Panel labels are in the same position throughout set Fonts used in labeling are Times, Times New Roman, Arial, Sabon, or Frutiger Color Figures are in RGB format and have an ICC color profile embedded. Authors have examined color View figures in CMYK to ensure color loss from RGB to CMYK conversion does not compromise the figure content (Print version is in CMYK; Online version is in RGB) FIGURE TYPES 1) Half-tone (photographic, continuous tone) Figures: - If in a rasterized file format (TIFF, Bitmap, etc…) Resolution minimum is 300dpi Size as intended for production - If in a presentation, line-art, or vector graphics format (Illustrator, PowerPoint)… Continuous tone images and scans were embedded with at least 300 DPI Fonts used were Times, Times New Roman, Arial, Sabon, or Frutiger Supported file format was used 2) Line-Art (vector graphics, schematics, graphs) Figures: - -

Picture Perfect the Real Story Behind Apple’S Retina Display Picture Perfect Seth Mcmurray
Seth McMurray Picture perfect The real story behind Apple’s Retina Display Picture perfect Seth McMurray The iPhone 4 was the first model different screen resolutions and pixel to feature Apple’s Retina Display, a densities. revolutionary new screen that far For example, the screen on a 13-inch surpassed the quality of any other Macbook Pro is physically much larger smartphone on the market at the time. To than that of the 3.5-inch iPhone 4S, and compare, the standard pixel density for while they both sport retina displays, the print quality is 300ppi (pixels per inch), Macbook Pro (227ppi) has a much lower and this new display was boasting 326ppi pixel density than the iPhone 4S (326ppi). on a mobile phone! It was a huge step These differences in pixel density (while forward for the industry, and future Apple still retaining the Retina label) are largely iPhone models continued with the Retina to do with the size of the screen, and standard of display quality. consequently, the intended viewing As stated by Apple: distance of the display. ‘The pixel density of Retina displays is so To put it simply, the bigger the screen, high that your eyes can’t detect individual the further away the optimal (or normal) pixels at a normal viewing distance. viewing distance is. This means that you This gives content incredible detail and can achieve the same ‘Retina’ effect dramatically improves your viewing (where the eye can’t distinguish individual experience.’ pixels) with less pixel density, because However, it seems that not all Retina the screen is intended to be viewed from displays are created equal, even with the further away. -

Tablet Display Technology Shoot-Out
frontline technology Tablet Display Technology Shoot-Out Smartphones and tablets represent a new class of displays with requirements different from that of TVs and monitors. Here is where manufacturers are – and are not – meeting the challenges of ambient light and other considerations. by Raymond M. Soneira MARTPHONES AND TABLETS In addition to being mobile computers that Tablet Displays and Display Technologies Srepresent a major product revolution for con- produce high-resolution text and graphics, The line between smartphones and tablets has sumers, but these mobile devices have had an these devices are also mobile HDTVs and become increasingly blurred, which has given even greater impact on the display industry. photo viewers. They are expected to deliver rise to an intermediate category called Up until recently, most display technology excellent picture quality and color accuracy phablets. For this article, I am classifying any was dedicated to producing large AC-powered over a wide range of ambient lighting. Their mobile display with a 5.5 in. or greater screen TVs and computer monitors that are used onboard digital cameras and their frequent use diagonal as a tablet. I picked a representative almost exclusively indoors under controlled for photo sharing among family and friends set of high-end displays and display technolo- and often subdued ambient lighting. Laptops make picture quality and color accuracy much gies in this size class, with the additional are the original mobile displays, but they have more important than for HDTVs because the requirement that they had to be tested on a hefty batteries, often run on AC power, and viewers often know what the photo subject production class device (rather than as a are also typically used indoors under con- matter actually looks like, especially when the standalone display or prototype). -

Resolution Explained
Resolution Explained Much confusion sometimes surrounds the question of just what resolution means in digital photography. Pixels, Pixels per Inch (PPI), Dots per Inch (DPI), dot density, screen size, print size and many other terms need a basic understanding to allow us to get the right combination for the task at hand. Pixel Pixel is a word coined by the photographic industry to describe the smallest element we can have in a digital photograph. Hence it is a picture element or pixel for short. A pixel is a single picture element and is the smallest element into which a photograph can be divided. A pixel can be only one colour, so a photograph is made up of a grid of thousands of pixels, each of varying colours that together make up the image. If you magnify a photograph enough, using an editing program, you will be able to see the individual pixels. PPI can be described as the pixel density of the image or the number of pixels in a unit of dimension. Resolution Resolution, in simple terms, is the total number of pixels available. You will most probably already have come across the term megapixel that is used because a pixel is actually very small and so generates large numbers. Technically a megapixel is equal to 1,048,576 pixels. In reality however, camera manufacturers round this number to 1,000,000 when stating the maximum resolution the camera will capture. This information does not specify the actual pixel dimensions of the image, only the total number of pixels in the image. -
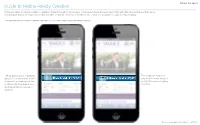
Guide to Retina Ready Creative
Yahoo! Ad Specs Guide to Retina Ready Creative Mobile and tablet ad creative is subject to appearing differently based on the resolution of the viewing device; because many mobile and tablet devices display at high resolu- tion (high pixel density) we request that mobile and tablet creative be created at 2x the dimensions of what they would be for a typical computer display. The examples below show two different sized ads on an iPhone 5 retina (high pixel density) display. The ad appears blurry or pixelated The ad appears sharp and because it is stretching out 320x50 crisp because it was designed to 640x100. Perceptually, the size at 640x100, and is not getting is 320x50, but since there is dou- stretched. ble the pixel density it equates to 640x100. *Please view .pdf at Actual Size, or100% Yahoo! Ad Specs Guide to Retina Ready Creative How ads appear on different pixel density displays: 320x50 ad on a low-pixel density display (typical computer display) The ad appears as it did when created. Perceptually, the size is 320x50, and the ad itself is 320x50. 320x50 ad on a high-pixel density display (retina) The ad appears blurry or pixelated because it is stretching 320x50 to 640x100. This image shows what is happening to the ad creative in this sce- nario. The ad was designed at 320x50 on a typical computer dis- play. Perceptually, the ad space will appear to be 320x50 on the high pixel density display, but since there is double the pixel density it equates to 640x100, so it is essentially stretching the graphic. -

Dissecting an Iphone 7 Plus
Dissecting an iPhone 7 Plus Donean Guerrero and Michael Benjamin iPhone 7+ ● Announced to the public on September 7th, 2016 ● Retail Price: $749 ● Cost of Materials to Build: $270.88 ● Introduced the “Two cameras that shoot as one”. ● This is the first iPhone that incorporated many new features and specs. Battery ● 2900 mAh lithium ion battery ● Most energetic rechargeable batteries available ● Lithium ion battery only loses about 5% of its charge per month ● Also 5% percent larger than the 2750 mAh battery used in the iPhone 6 Plus ● Battery life goes up to 21 hours talk time Rear Camera/Front Camera ● The rear camera is 12 megapixels and the front camera is 7 megapixels ● This is Apple’s first time introducing a dual lens camera system. ● 2x Optical Zoom. ● This creates a depth of field effect. ● Optical Image Stabilization ● Shoots in 4k ● Sapphire Crystal lens cover ● https://www.youtube.com/watch?v=EZL4rwTB8Yg Cell Antenna ● Allows the phone to send and receive cellular waves, WiFi and bluetooth signals. ● Located on the top of the phone. Loudspeaker ● Uses both the primary speaker and the earpiece speaker. ● This produces a stereo sound ● Better performance than previous models Barometric Vent ● This was something new that apple added to their phones ● This replaced the headphone jack that all previous iPhones had ● Bottom left side of your iPhone is not a speaker it is where they placed the Barometer ● Since they added waterproofing they needed to add the Barometer ● The barometer allows a phone to measure altitude and pressure ● It can even measure minor changes like climbing a flight of stairs Taptic Engine ● Provides tactile sensation in the form of vibrations to users ● Senses the amount of fingerprint pressure applied to the display ● Users of Apple devices feel sensations that vary based on the type of feedback provided, which allows the device to quickly convey information without the user needing to look at a screen or display. -

Fact Sheet NOOK® HD and NOOK® HD+ Highly Acclaimed
Fact Sheet NOOK® HD and NOOK® HD+ – Highly Acclaimed, Lightweight, High-Definition 7- and 9-Inch Tablets Featuring Google Play™ NOOK HD and NOOK HD+ offer incredible reading and entertainment like never seen before on 7- and 9-inch tablets. Browse the NOOK Store®, one of the world’s largest digital bookstores with more than 3 million titles, enjoy movies and TV shows in brilliant but portable HD resolution and discover an unparalleled reading experience with beautifully rendered text and lightning fast page turns. Surf favorite websites using the super-fast Web browser; stay connected with family, friends and colleagues through built-in email, and enjoy movies and TV shows on a high resolution display 7-inch tablet or must-see 9-inch form factor. Designed for both personal use and the whole family to share, NOOK HD and NOOK HD+ unlock an instantly personalized experience with individual profiles for each member of the family, allowing children to freely dive into their collection of digital picture books, learning apps and kid-friendly videos without happening upon mom and dad’s books, magazines and more. With Google Play on NOOK HD and NOOK HD+, customers have access to more than 700,000 Android apps and games, millions of songs and more. Barnes & Noble’s highly acclaimed, lightweight, high-definition 7- and 9-inch tablets also include popular Google services like the Chrome™ browser, Gmail™, YouTube™, Google Search™ and Google Maps™. Spectacular Display, Super-Light Packed with 243 pixels per inch, NOOK HD offers a high-resolution display on a 7-inch media tablet, and is incredibly light at only 11.1 ounces (315 grams). -

Optimizing Smartphone Power Consumption Through Dynamic Resolution Scaling
Optimizing Smartphone Power Consumption through Dynamic Resolution Scaling Songtao He1;2, Yunxin Liu1, Hucheng Zhou1 1Microsoft Research, Beijing, China 2University of Science and Technology of China, Hefei, China [email protected], {yunliu, huzho}@microsoft.com ABSTRACT Keywords The extremely-high display density of modern smartphones Smartphone; GPU; Power Consumption; Display Resolu- imposes a significant burden on power consumption, yet does tion; Dynamic Resolution Scaling not always provide an improved user experience and may even lead to a compromised user experience. As human visually-perceivable ability highly depends on the user-screen distance, a reduced display resolution may still achieve the 1. INTRODUCTION same user experience when the user-screen distance is large. The display resolution of smartphones has become increas- This provides new power-saving opportunities. In this pa- ingly high. Since the \Retina display" of the iPhone 4 re- per, we present a flexible dynamic resolution scaling system leased in 2010 [18], display resolution of smartphones has for smartphones. The system adopts an ultrasonic-based continued to rise, from 960x640 pixels of the iPhone 4 to approach to accurately detect the user-screen distance at 1920x1080 pixels (Full HD) and recently to 2560x1440 pixels low-power cost and makes scaling decisions automatically (2K). As a result, latest smartphones have an extremely-high for maximum user experience and power saving. App de- display density. For example, the LG G3 [16] has a display velopers or users can also adjust the resolution manually as of 538 pixels per inch (ppi), while the Samsung Galaxy S5 their needs. Our system is able to work on existing commer- LTE-A [17] has a display of 577 ppi. -

Subpixel Shuto for Display Energy Reduction on OLED Smartphones
Too Many Pixels to Perceive: Subpixel Shuto for Display Energy Reduction on OLED Smartphones Zhisheng Yan Chang Wen Chen Georgia State University State University of New York at Bualo ABSTRACT experience in regular use cases. Instead, it will even drain much Organic lightemitting diode (OLED) has been widely recognized more display power and degrade user experience [27]. as the nextgeneration mobile display. Recently, smartphone manu In particular, most manufacturers have pushed up their OLED facturers have been pushing up the pixel density of OLED display. smartphone resolution to 2560 ×1440 (2K), which boosts the display Unfortunately, such an eort does not necessarily improve the pixel density to more than 500 Pixels Per Inch (PPI ). Despite these everyday viewing because of the limitation in human visual acuity. impressive statistics, a wellknown issue is that users are unlikely Instead, high pixel density OLED can drain the battery power even to dierentiate such subtle content detail in normal usage because more quickly since the power dissipation of OLED is determined of the limitation in human visual acuity. According to an image by the number of displayed pixels and their RGB values, or sub viewing study [ 26 ], one half of the subjects identied a 577PPI pixels. This paper presents a new design dimension to remedy this OLED phone as a better display while the other half preferred a prevailing issue by leveraging the intuition that shutting o redun samesize phone with 471 PPI. The reason for this controversy is dant subpixels of the display content on OLED can reduce power that the extremely high PPI makes each pixel shrunk to an indis consumption without impacting viewing perception.