Today. Complete Graph. K4 and K5 a Tree, a Tree. Trees. Equivalence Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

On Treewidth and Graph Minors
On Treewidth and Graph Minors Daniel John Harvey Submitted in total fulfilment of the requirements of the degree of Doctor of Philosophy February 2014 Department of Mathematics and Statistics The University of Melbourne Produced on archival quality paper ii Abstract Both treewidth and the Hadwiger number are key graph parameters in structural and al- gorithmic graph theory, especially in the theory of graph minors. For example, treewidth demarcates the two major cases of the Robertson and Seymour proof of Wagner's Con- jecture. Also, the Hadwiger number is the key measure of the structural complexity of a graph. In this thesis, we shall investigate these parameters on some interesting classes of graphs. The treewidth of a graph defines, in some sense, how \tree-like" the graph is. Treewidth is a key parameter in the algorithmic field of fixed-parameter tractability. In particular, on classes of bounded treewidth, certain NP-Hard problems can be solved in polynomial time. In structural graph theory, treewidth is of key interest due to its part in the stronger form of Robertson and Seymour's Graph Minor Structure Theorem. A key fact is that the treewidth of a graph is tied to the size of its largest grid minor. In fact, treewidth is tied to a large number of other graph structural parameters, which this thesis thoroughly investigates. In doing so, some of the tying functions between these results are improved. This thesis also determines exactly the treewidth of the line graph of a complete graph. This is a critical example in a recent paper of Marx, and improves on a recent result by Grohe and Marx. -

Graph Varieties Axiomatized by Semimedial, Medial, and Some Other Groupoid Identities
Discussiones Mathematicae General Algebra and Applications 40 (2020) 143–157 doi:10.7151/dmgaa.1344 GRAPH VARIETIES AXIOMATIZED BY SEMIMEDIAL, MEDIAL, AND SOME OTHER GROUPOID IDENTITIES Erkko Lehtonen Technische Universit¨at Dresden Institut f¨ur Algebra 01062 Dresden, Germany e-mail: [email protected] and Chaowat Manyuen Department of Mathematics, Faculty of Science Khon Kaen University Khon Kaen 40002, Thailand e-mail: [email protected] Abstract Directed graphs without multiple edges can be represented as algebras of type (2, 0), so-called graph algebras. A graph is said to satisfy an identity if the corresponding graph algebra does, and the set of all graphs satisfying a set of identities is called a graph variety. We describe the graph varieties axiomatized by certain groupoid identities (medial, semimedial, autodis- tributive, commutative, idempotent, unipotent, zeropotent, alternative). Keywords: graph algebra, groupoid, identities, semimediality, mediality. 2010 Mathematics Subject Classification: 05C25, 03C05. 1. Introduction Graph algebras were introduced by Shallon [10] in 1979 with the purpose of providing examples of nonfinitely based finite algebras. Let us briefly recall this concept. Given a directed graph G = (V, E) without multiple edges, the graph algebra associated with G is the algebra A(G) = (V ∪ {∞}, ◦, ∞) of type (2, 0), 144 E. Lehtonen and C. Manyuen where ∞ is an element not belonging to V and the binary operation ◦ is defined by the rule u, if (u, v) ∈ E, u ◦ v := (∞, otherwise, for all u, v ∈ V ∪ {∞}. We will denote the product u ◦ v simply by juxtaposition uv. Using this representation, we may view any algebraic property of a graph algebra as a property of the graph with which it is associated. -
![Arxiv:2006.06067V2 [Math.CO] 4 Jul 2021](https://docslib.b-cdn.net/cover/6166/arxiv-2006-06067v2-math-co-4-jul-2021-416166.webp)
Arxiv:2006.06067V2 [Math.CO] 4 Jul 2021
Treewidth versus clique number. I. Graph classes with a forbidden structure∗† Cl´ement Dallard1 Martin Milaniˇc1 Kenny Storgelˇ 2 1 FAMNIT and IAM, University of Primorska, Koper, Slovenia 2 Faculty of Information Studies, Novo mesto, Slovenia [email protected] [email protected] [email protected] Treewidth is an important graph invariant, relevant for both structural and algo- rithmic reasons. A necessary condition for a graph class to have bounded treewidth is the absence of large cliques. We study graph classes closed under taking induced subgraphs in which this condition is also sufficient, which we call (tw,ω)-bounded. Such graph classes are known to have useful algorithmic applications related to variants of the clique and k-coloring problems. We consider six well-known graph containment relations: the minor, topological minor, subgraph, induced minor, in- duced topological minor, and induced subgraph relations. For each of them, we give a complete characterization of the graphs H for which the class of graphs excluding H is (tw,ω)-bounded. Our results yield an infinite family of χ-bounded induced-minor-closed graph classes and imply that the class of 1-perfectly orientable graphs is (tw,ω)-bounded, leading to linear-time algorithms for k-coloring 1-perfectly orientable graphs for every fixed k. This answers a question of Breˇsar, Hartinger, Kos, and Milaniˇc from 2018, and one of Beisegel, Chudnovsky, Gurvich, Milaniˇc, and Servatius from 2019, respectively. We also reveal some further algorithmic implications of (tw,ω)- boundedness related to list k-coloring and clique problems. In addition, we propose a question about the complexity of the Maximum Weight Independent Set prob- lem in (tw,ω)-bounded graph classes and prove that the problem is polynomial-time solvable in every class of graphs excluding a fixed star as an induced minor. -
![Arxiv:1906.05510V2 [Math.AC]](https://docslib.b-cdn.net/cover/0166/arxiv-1906-05510v2-math-ac-660166.webp)
Arxiv:1906.05510V2 [Math.AC]
BINOMIAL EDGE IDEALS OF COGRAPHS THOMAS KAHLE AND JONAS KRUSEMANN¨ Abstract. We determine the Castelnuovo–Mumford regularity of binomial edge ideals of complement reducible graphs (cographs). For cographs with n vertices the maximum regularity grows as 2n/3. We also bound the regularity by graph theoretic invariants and construct a family of counterexamples to a conjecture of Hibi and Matsuda. 1. Introduction Let G = ([n], E) be a simple undirected graph on the vertex set [n]= {1,...,n}. x1 ··· xn x1 ··· xn Let X = ( y1 ··· yn ) be a generic 2 × n matrix and S = k[ y1 ··· yn ] the polynomial ring whose indeterminates are the entries of X and with coefficients in a field k. The binomial edge ideal of G is JG = hxiyj −yixj : {i, j} ∈ Ei⊆ S, the ideal of 2×2 mi- nors indexed by the edges of the graph. Since their inception in [5, 15], connecting combinatorial properties of G with algebraic properties of JG or S/ JG has been a popular activity. Particular attention has been paid to the minimal free resolution of S/ JG as a standard N-graded S-module [3, 11]. The data of a minimal free res- olution is encoded in its graded Betti numbers βi,j (S/ JG) = dimk Tori(S/ JG, k)j . An interesting invariant is the highest degree appearing in the resolution, the Castelnuovo–Mumford regularity reg(S/ JG) = max{j − i : βij (S/ JG) 6= 0}. It is a complexity measure as low regularity implies favorable properties like vanish- ing of local cohomology. Binomial edge ideals have square-free initial ideals by arXiv:1906.05510v2 [math.AC] 10 Mar 2021 [5, Theorem 2.1] and, using [1], this implies that the extremal Betti numbers and regularity can also be derived from those initial ideals. -

Treewidth-Erickson.Pdf
Computational Topology (Jeff Erickson) Treewidth Or il y avait des graines terribles sur la planète du petit prince . c’étaient les graines de baobabs. Le sol de la planète en était infesté. Or un baobab, si l’on s’y prend trop tard, on ne peut jamais plus s’en débarrasser. Il encombre toute la planète. Il la perfore de ses racines. Et si la planète est trop petite, et si les baobabs sont trop nombreux, ils la font éclater. [Now there were some terrible seeds on the planet that was the home of the little prince; and these were the seeds of the baobab. The soil of that planet was infested with them. A baobab is something you will never, never be able to get rid of if you attend to it too late. It spreads over the entire planet. It bores clear through it with its roots. And if the planet is too small, and the baobabs are too many, they split it in pieces.] — Antoine de Saint-Exupéry (translated by Katherine Woods) Le Petit Prince [The Little Prince] (1943) 11 Treewidth In this lecture, I will introduce a graph parameter called treewidth, that generalizes the property of having small separators. Intuitively, a graph has small treewidth if it can be recursively decomposed into small subgraphs that have small overlap, or even more intuitively, if the graph resembles a ‘fat tree’. Many problems that are NP-hard for general graphs can be solved in polynomial time for graphs with small treewidth. Graphs embedded on surfaces of small genus do not necessarily have small treewidth, but they can be covered by a small number of subgraphs, each with small treewidth. -

Subgraph Isomorphism in Graph Classes
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Discrete Mathematics 312 (2012) 3164–3173 Contents lists available at SciVerse ScienceDirect Discrete Mathematics journal homepage: www.elsevier.com/locate/disc Subgraph isomorphism in graph classes Shuji Kijima a, Yota Otachi b, Toshiki Saitoh c,∗, Takeaki Uno d a Graduate School of Information Science and Electrical Engineering, Kyushu University, Fukuoka, 819-0395, Japan b School of Information Science, Japan Advanced Institute of Science and Technology, Ishikawa, 923-1292, Japan c Graduate School of Engineering, Kobe University, Kobe, 657-8501, Japan d National Institute of Informatics, Tokyo, 101-8430, Japan article info a b s t r a c t Article history: We investigate the computational complexity of the following restricted variant of Received 17 September 2011 Subgraph Isomorphism: given a pair of connected graphs G D .VG; EG/ and H D .VH ; EH /, Received in revised form 6 July 2012 determine if H is isomorphic to a spanning subgraph of G. The problem is NP-complete in Accepted 9 July 2012 general, and thus we consider cases where G and H belong to the same graph class such as Available online 28 July 2012 the class of proper interval graphs, of trivially perfect graphs, and of bipartite permutation graphs. For these graph classes, several restricted versions of Subgraph Isomorphism Keywords: such as , , , and can be solved Subgraph isomorphism Hamiltonian Path Clique Bandwidth Graph Isomorphism Graph class in polynomial time, while these problems are hard in general. NP-completeness ' 2012 Elsevier B.V. -
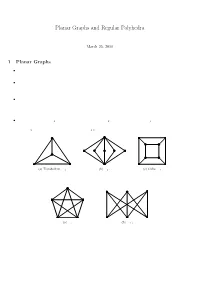
Planar Graphs and Regular Polyhedra
Planar Graphs and Regular Polyhedra March 25, 2010 1 Planar Graphs ² A graph G is said to be embeddable in a plane, or planar, if it can be drawn in the plane in such a way that no two edges cross each other. Such a drawing is called a planar embedding of the graph. ² Let G be a planar graph and be embedded in a plane. The plane is divided by G into disjoint regions, also called faces of G. We denote by v(G), e(G), and f(G) the number of vertices, edges, and faces of G respectively. ² Strictly speaking, the number f(G) may depend on the ways of drawing G on the plane. Nevertheless, we shall see that f(G) is actually independent of the ways of drawing G on any plane. The relation between f(G) and the number of vertices and the number of edges of G are related by the well-known Euler Formula in the following theorem. ² The complete graph K4, the bipartite complete graph K2;n, and the cube graph Q3 are planar. They can be drawn on a plane without crossing edges; see Figure 5. However, by try-and-error, it seems that the complete graph K5 and the complete bipartite graph K3;3 are not planar. (a) Tetrahedron, K4 (b) K2;5 (c) Cube, Q3 Figure 1: Planar graphs (a) K5 (b) K3;3 Figure 2: Nonplanar graphs Theorem 1.1. (Euler Formula) Let G be a connected planar graph with v vertices, e edges, and f faces. Then v ¡ e + f = 2: (1) 1 (a) Octahedron (b) Dodecahedron (c) Icosahedron Figure 3: Regular polyhedra Proof. -

What Is a Polyhedron?
3. POLYHEDRA, GRAPHS AND SURFACES 3.1. From Polyhedra to Graphs What is a Polyhedron? Now that we’ve covered lots of geometry in two dimensions, let’s make things just a little more difficult. We’re going to consider geometric objects in three dimensions which can be made from two-dimensional pieces. For example, you can take six squares all the same size and glue them together to produce the shape which we call a cube. More generally, if you take a bunch of polygons and glue them together so that no side gets left unglued, then the resulting object is usually called a polyhedron.1 The corners of the polygons are called vertices, the sides of the polygons are called edges and the polygons themselves are called faces. So, for example, the cube has 8 vertices, 12 edges and 6 faces. Different people seem to define polyhedra in very slightly different ways. For our purposes, we will need to add one little extra condition — that the volume bound by a polyhedron “has no holes”. For example, consider the shape obtained by drilling a square hole straight through the centre of a cube. Even though the surface of such a shape can be constructed by gluing together polygons, we don’t consider this shape to be a polyhedron, because of the hole. We say that a polyhedron is convex if, for each plane which lies along a face, the polyhedron lies on one side of that plane. So, for example, the cube is a convex polyhedron while the more complicated spec- imen of a polyhedron pictured on the right is certainly not convex. -
5 Graph Theory
last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples. -

Crossing Number for Graphs with Bounded Pathwidth∗†
Crossing Number for Graphs with Bounded Pathwidth∗† Therese Biedl‡1, Markus Chimani§2, Martin Derka¶3, and Petra Mutzel‖4 1 Dept. of Computer Science, University of Waterloo, Canada [email protected] 2 Dept. of Computer Science, Universität Osnabrück, Germany [email protected] 3 Dept. of Computer Science, University of Waterloo, Canada [email protected] 4 Dept. of Computer Science, Technische Universität Dortmund, Germany [email protected] Abstract The crossing number is the smallest number of pairwise edge crossings when drawing a graph into the plane. There are only very few graph classes for which the exact crossing number is known or for which there at least exist constant approximation ratios. Furthermore, up to now, general crossing number computations have never been successfully tackled using bounded width of graph decompositions, like treewidth or pathwidth. In this paper, we for the first time show that crossing number is tractable (even in linear time) for maximal graphs of bounded pathwidth 3. The technique also shows that the crossing number and the rectilinear (a.k.a. straight-line) crossing number are identical for this graph class, and that we require only an O(n) × O(n)-grid to achieve such a drawing. Our techniques can further be extended to devise a 2-approximation for general graphs with pathwidth 3, and a 4w3-approximation for maximal graphs of pathwidth w. This is a constant approximation for bounded pathwidth graphs. 1998 ACM Subject Classification F.2.2 Nonnumerical Algorithms and Problems Keywords and phrases Crossing Number, Graphs with Bounded Pathwidth Digital Object Identifier 10.4230/LIPIcs.ISAAC.2017.13 1 Introduction The crossing number cr(G) is the smallest number of pairwise edge-crossings over all possible drawings of a graph G into the plane. -

Algorithmic Graph Theory Part III Perfect Graphs and Their Subclasses
Algorithmic Graph Theory Part III Perfect Graphs and Their Subclasses Martin Milanicˇ [email protected] University of Primorska, Koper, Slovenia Dipartimento di Informatica Universita` degli Studi di Verona, March 2013 1/55 What we’ll do 1 THE BASICS. 2 PERFECT GRAPHS. 3 COGRAPHS. 4 CHORDAL GRAPHS. 5 SPLIT GRAPHS. 6 THRESHOLD GRAPHS. 7 INTERVAL GRAPHS. 2/55 THE BASICS. 2/55 Induced Subgraphs Recall: Definition Given two graphs G = (V , E) and G′ = (V ′, E ′), we say that G is an induced subgraph of G′ if V ⊆ V ′ and E = {uv ∈ E ′ : u, v ∈ V }. Equivalently: G can be obtained from G′ by deleting vertices. Notation: G < G′ 3/55 Hereditary Graph Properties Hereditary graph property (hereditary graph class) = a class of graphs closed under deletion of vertices = a class of graphs closed under taking induced subgraphs Formally: a set of graphs X such that G ∈ X and H < G ⇒ H ∈ X . 4/55 Hereditary Graph Properties Hereditary graph property (Hereditary graph class) = a class of graphs closed under deletion of vertices = a class of graphs closed under taking induced subgraphs Examples: forests complete graphs line graphs bipartite graphs planar graphs graphs of degree at most ∆ triangle-free graphs perfect graphs 5/55 Hereditary Graph Properties Why hereditary graph classes? Vertex deletions are very useful for developing algorithms for various graph optimization problems. Every hereditary graph property can be described in terms of forbidden induced subgraphs. 6/55 Hereditary Graph Properties H-free graph = a graph that does not contain H as an induced subgraph Free(H) = the class of H-free graphs Free(M) := H∈M Free(H) M-free graphT = a graph in Free(M) Proposition X hereditary ⇐⇒ X = Free(M) for some M M = {all (minimal) graphs not in X} The set M is the set of forbidden induced subgraphs for X. -

Treewidth and Pathwidth of Permutation Graphs
Treewidth and pathwidth of permutation graphs Citation for published version (APA): Bodlaender, H. L., Kloks, A. J. J., & Kratsch, D. (1992). Treewidth and pathwidth of permutation graphs. (Universiteit Utrecht. UU-CS, Department of Computer Science; Vol. 9230). Utrecht University. Document status and date: Published: 01/01/1992 Document Version: Publisher’s PDF, also known as Version of Record (includes final page, issue and volume numbers) Please check the document version of this publication: • A submitted manuscript is the version of the article upon submission and before peer-review. There can be important differences between the submitted version and the official published version of record. People interested in the research are advised to contact the author for the final version of the publication, or visit the DOI to the publisher's website. • The final author version and the galley proof are versions of the publication after peer review. • The final published version features the final layout of the paper including the volume, issue and page numbers. Link to publication General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal.