Join Query Optimization Techniques for Complex Event Processing Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Distributed Complex Event Processing in Multiclouds
Distributed Complex Event Processing in Multiclouds Vassilis Stefanidis1, Yiannis Verginadis1, Ioannis Patiniotakis1 and Gregoris Mentzas1 1 Institute of Communications and Computer Systems, National Technical University of Ath- ens, Greece {stefanidis, jverg, ipatini, gmentzas}@mail.ntua.gr Abstract. The last few years, the generation of vast amounts of heterogeneous data with different velocity and veracity and the requirement to process them, has significantly challenged the computational capacity and efficiency of the modern infrastructural resources. The propagation of Big Data among different pro- cessing and storage architectures, has amplified the need for adequate and cost- efficient infrastructures to host them. An overabundance of cloud service offer- ings is currently available and is being rapidly adopted by small and medium enterprises based on its many benefits to traditional computing models. However, at the same time the Big Data computing requirements pose new research chal- lenges that question the adoption of single cloud provider resources. Nowadays, we discuss the emerging data-intensive applications that necessitate the wide adoption of multicloud deployment models, in order to use all the advantages of cloud computing. A key tool for managing such multicloud applications and guarantying their quality of service, even in extreme scenarios of workload fluc- tuations, are adequate distributed monitoring mechanisms. In this work, we dis- cuss a distributed complex event processing architecture that follows automati- cally the big data application deployment in order to efficiently monitor its health status and detect reconfiguration opportunities. This proposal is examined against an illustrative scenario and is preliminary evaluated for revealing its performance results. Keywords: Distributed CEP, Cloud Monitoring, Multiclouds, Big Data. -

Efficient Pattern Matching Over Event Streams
Efficient Pattern Matching over Event Streams ∗ Jagrati Agrawal, Yanlei Diao, Daniel Gyllstrom, and Neil Immerman Department of Computer Science University of Massachusetts Amherst Amherst, MA, USA fjagrati, yanlei, dpg, [email protected] ABSTRACT against complex patterns and the events used to match each Pattern matching over event streams is increasingly being pattern are transformed into new events for output. Re- employed in many areas including financial services, RFID- cently, such pattern matching over streams has aroused sig- based inventory management, click stream analysis, and elec- nificant interest in industry [28, 30, 29, 9] due to its wide tronic health systems. While regular expression matching applicability in areas such as financial services [10], RFID- is well studied, pattern matching over streams presents two based inventory management [31], click stream analysis [26], new challenges: Languages for pattern matching over streams and electronic health systems [16]. In financial services, for are significantly richer than languages for regular expression instance, a brokerage customer may be interested in a se- matching. Furthermore, efficient evaluation of these pattern quence of stock trading events that represent a new market queries over streams requires new algorithms and optimiza- trend. In RFID-based tracking and monitoring, applica- tions: the conventional wisdom for stream query processing tions may want to track valid paths of shipments and detect (i.e., using selection-join-aggregation) is inadequate. anomalies such as food contamination in supply chains. In this paper, we present a formal evaluation model that While regular expression matching is a well studied com- offers precise semantics for this new class of queries and a puter science problem [17], pattern matching over streams query evaluation framework permitting optimizations in a presents two new challenges: principled way. -

Darko Anicic Event Processing and Stream Reasoning with ETALIS
Darko Anicic Event Processing and Stream Reasoning with ETALIS Zur Erlangung des akademischen Grades eines Doktors der Wirtschaftswissenschaften (Dr. rer. pol.) von der Fakultät für Wirtschaftswissenschaften des Karlsruher Instituts für Technologie (KIT) genehmigte Dissertation. Event Processing and Stream Reasoning with ETALIS Dipl.-Ing. Darko Aniciˇ c´ Referent: Prof. Dr. Rudi Studer Korreferent: Prof. Dr. Opher Etzion Prüfer: Prof. Dr. Detlef Seese Vorsitzender der Prüfungskommission: Prof. Dr. Andreas Geyer-Schulz Tag der mündlichen Prüfung: 09. November 2011. Institut für Angewandte Informatik und Formale Beschreibungsverfahren (AIFB) Fakultät Wirtschaftswissenschaften Karlsruher Institut für Technologie (KIT) Karlsruhe 2011 i To Vedrana and Andre Abstract Event Processing (EP) is concerned with detection of situations under time constraints that are of a particular business interest. We face today a paradigm shift toward the real time information processing, and EP has therefore spawned significant attention in science and technology. Due to omnipresence of events, EP is becoming a central as- pect of new distributed systems such as cloud computing and grid systems, mobile and sensor-based systems, as well as a number of application areas including financial ser- vices, business intelligence, social and collaborative networking, click stream analysis and many others. However, there are a number of issues to be considered in order to enable effective event-based computation. A language for describing event patterns needs to feature a well-defined semantics. It also needs to be rich enough to express important classes of event patterns. Pattern matching should be supported in both, query-driven and event- driven modes. A number of other event operations, such as event aggregation, filtering, translation, enrichment and splitting, should be supported too. -

Cayuga: a General Purpose Event Monitoring System
Cayuga: A General Purpose Event Monitoring System Alan Demers1, Johannes Gehrke1, Biswanath Panda1 ∗ † Mirek Riedewald1, Varun Sharma2 , and Walker White1 1Department of Computer Science, Cornell University 2Computer Science and Engineering, Indian Institute of Technology Delhi ABSTRACT number of concurrent queries registered in the event processing We describe the design and implementation of the Cornell Cayuga system. This is similar to the workload of publish/subscribe sys- System for scalable event processing. We present a query language tems. In comparison, data stream management systems are usually based on Cayuga Algebra for naturally expressing complex event less scalable in the number of queries, capable of supporting only patterns. We also describe several novel system design and im- a small number of concurrent queries. plementation issues, focusing on Cayuga’s query processor, its in- We have designed and built Cayuga, a general-purpose system dexing approach, how Cayuga handles simultaneous events, and its for processing complex events on a large scale [8]. Cayuga supports specialized garbage collector. on-line detection of a large number of complex patterns in event streams. Event patterns are written in a query language based on operators which have well-defined formal semantics. This enables 1. INTRODUCTION Cayuga to perform query-rewrite optimizations. All operators are A large class of both well-established and emerging applications composable, allowing Cayuga to build up complex patterns from can best be described as -

Episodic Memory Representation in a Knowledge Base, with Application to Event Monitoring and Event Detection
Episodic Memory Representation in a Knowledge Base, with Application to Event Monitoring and Event Detection Master’s Thesis Engin C¸ınar S¸ahin Committee Members Scott E. Fahlman Eric Nyberg Stephen F. Smith Language Technologies Institute School of Computer Science Carnegie Mellon University Pittsburgh, PA, 15213 Abstract The thesis explores the use of a knowledge-based AI system to assist people in executing proce- dures and detecting events in an observed world. We extend the Scone knowledge-base system with open-ended facilities for representing time and events. Then we use this episodic knowledge repre- sentation as the foundation for our event monitoring and event detection algorithms. This approach lets us represent and reason about three fundamental aspects of the observed events: 1. their ontological character and what entities take part in these events (e.g. buying is a kind of transaction that involves an agent, a seller, money and goods) 2. how events change the world over time (e.g. after a buy event the agent has the goods rather than the money) 3. how events may be composed of other subevents (i.e. a buy event may be composed of giving money and receiving goods) We illustrate knowledge-based solutions to the event monitoring problem in the conference organization domain and to the event detection problem in the national security domain. i Acknowledgements First, I would like to thank my advisor Scott Fahlman for letting me learn so much from him. His invaluable experience and constant support helped me go through the ups and downs of research. Working with him, his passion and excitement for knowledge representation and reasoning has passed on to me. -

Requirements and State of the Art Overview on Flexible Event Processing
ICT, STREP FERARI ICT-FP7-619491 Flexible Event pRocessing for big dAta aRchItectures Collaborative Project D4.1 Requirements and state of the art overview of flexible event processing 01.02.2013 – 31.01.2014(preparation period) Contractual Date of Delivery: 31.01.2015 Actual Date of Delivery: 31.01.2015 Author(s): Fabiana Fournier and Inna Skarbovsky Institution: IBM Workpackage: Flexible Event Processing Security: PU Nature: R Total number of pages: 48 Project funded by the European Community under the Information and Communication Technologies Programme Contract ICT-FP7-619491 Project coordinator name Michael Mock Revision: 1 Project coordinator organisation name Fraunhofer Institute for Intelligent Analysis and Information Systems (IAIS) Schloss Birlinghoven, 53754 Sankt Augustin, Germany URL: http://www.iais.fraunhofer.de Abstract The goal of the FERARI (Flexible Event pRocessing for big dAta aRchItectures) project is to pave the way for efficient real-time Big Data technologies of the future. The proposed framework aims at enabling business users to express complex analytics tasks through a high-level declarative language that supports distributed complex event processing as an integral part of the system architecture. Work package 4 “Flexible Event Processing” deals with all the developments around event processing technologies in order to achieve this goal. In order to be flexible, event processing engines need to tackle the two following requirements in a satisfactory way: • The easy adaptability to non-functional requirements, specially, the way the tool copes with scalability issues in a distributed environment. • The easy definition and maintenance of the event-driven logic. The task of work package 4 is to provide a model and methodology to cope with these limitations. -

Complex Event Processing As a Service in Multi-Cloud Environments
Western University Scholarship@Western Electronic Thesis and Dissertation Repository August 2016 Complex Event Processing as a Service in Multi-Cloud Environments Wilson A. Higashino The University of Western Ontario Supervisor Dr. Miriam A. M. Capretz The University of Western Ontario Graduate Program in Electrical and Computer Engineering A thesis submitted in partial fulfillment of the equirr ements for the degree in Doctor of Philosophy © Wilson A. Higashino 2016 Follow this and additional works at: https://ir.lib.uwo.ca/etd Part of the Databases and Information Systems Commons Recommended Citation Higashino, Wilson A., "Complex Event Processing as a Service in Multi-Cloud Environments" (2016). Electronic Thesis and Dissertation Repository. 4016. https://ir.lib.uwo.ca/etd/4016 This Dissertation/Thesis is brought to you for free and open access by Scholarship@Western. It has been accepted for inclusion in Electronic Thesis and Dissertation Repository by an authorized administrator of Scholarship@Western. For more information, please contact [email protected]. Abstract The rise of mobile technologies and the Internet of Things, combined with advances in Web technologies, have created a new Big Data world in which the volume and velocity of data gen- eration have achieved an unprecedented scale. As a technology created to process continuous streams of data, Complex Event Processing (CEP) has been often related to Big Data and used as a tool to obtain real-time insights. However, despite this recent surge of interest, the CEP market is still dominated by solutions that are costly and inflexible or too low-level and hard to operate. To address these problems, this research proposes the creation of a CEP system that can be o↵ered as a service and used over the Internet. -

Concepts of Concurrent Programming
C U R R I C U L U M M O D U L E SEI-CM-24 Carnegie Mellon University Software Engineering Institute Concepts of Concurrent Programming . David W. Bustard University of Ulster April 1990 Approved for public release. Distribution unlimited. Preface A concurrent program is one defining actions that may be performed Capsule simultaneously. This module discusses the nature of such programs Description and provides an overview of the means by which they may be constructed and executed. Emphasis is given to the terminology used in this field and the underlying concepts involved. This module is largely concerned with explicit concurrency, where Scope concurrent behavior is specified by the program designer. Particular attention is paid to programs that can be considered inherently concurrent, that is, programs that are constructed to control or model physical systems that involve parallel activity. The module also includes a brief introduction to performance-oriented concurrency, where concurrency is used to improve program performance by taking advantage of hardware support for parallel processing. The module is divided into three sections. The first deals with basic concepts in concurrent programming, covering characteristic attributes, formal properties, standard design problems, and execution details. The second section discusses the steps in constructing concurrent programs from specification to coding. The final section briefly examines concurrency from the point of view of some common application areas. The module gives a foundation for a deeper study of specific topics in concurrent programming. It also provides the preparatory material for a study of the concurrent aspects of application areas such as real-time (embedded) systems, database systems, operating systems, and many simulation systems. -
So Many Performance Events, So Little Time
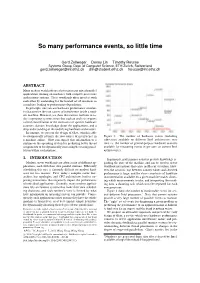
So many performance events, so little time Gerd Zellweger Denny Lin Timothy Roscoe Systems Group, Dept. of Computer Science, ETH Zurich, Switzerland [email protected] [email protected] [email protected] ABSTRACT Many modern workloads are a heterogeneous mix of parallel applications running on machines with complex processors and memory systems. These workloads often interfere with each other by contending for the limited set of resources in a machine, leading to performance degradation. In principle, one can use hardware performance counters to characterize the root causes of interference inside a mod- ern machine. However, we show that current facilities in to- day’s operating systems mean that such an analysis requires careful consideration of the intricacies of specific hardware counters, domain knowledge about the applications, and a deep understanding of the underlying hardware architecture. In contrast, we present the design of Glatt, which is able to automatically identify the root causes of interference in Figure 1: The number of hardware events (including a machine online. Glatt can expose this information to a subevents) available on different Intel architectures over runtime or the operating system for predicting better thread time vs. the number of general-purpose hardware counters assignments or for dynamically increasing/decreasing paral- available for measuring events (8 per core on current Intel lelism within each runtime. architectures). 1. INTRODUCTION In principle, performance counters provide knowledge re- Modern server workloads are often a mix of different ap- garding the state of the machine and can be used to detect plications, each with their own parallel runtime. -

Windows OS Event Correlation
TALLINN UNIVERSITY OF TECHNOLOGY Faculty of Information Technology Department of Computer Science TUT Centre for Digital Forensics and Cyber Security ITC70LT Mina Gerges - 114381IVCMM LOG MONITORING AND EVENT CORRELATION ON MICROSOFT® WINDOWS™ USING SIMPLE EVENT CORRELATOR Master thesis Supervisor: Risto Vaarandi Doctor of Philosophy Senior Researcher Tallinn 2016 TALLINNA TEHNIKAÜLIKOOL Infotehnoloogia teaduskond Arvutiteaduse instituut TTÜ Küberkriminalistika ja Küberjulgeoleku Keskus ITC70LT Mina Gerges - 114381IVCMM LOGIDE MONITOORING JA SÜNDMUSTE KORRELATSIOON MICROSOFT® WINDOWS™ PLATVORMIL SEC KORRELATSIOONIMOOTORI ABIL Magistritöö Juhendaja: Risto Vaarandi Filosoofiadoktor Vanemteadur Tallinn 2016 Declaration I hereby declare that I am the sole author of this thesis. All the used materials, references to the literature and the work of others have been referred to. This thesis has not been presented for examination anywhere else. Author: Mina Gerges ……………………………………. ……………………………… (Date) (Signature) 2 Abstract The aim of this thesis is providing a stable integration solution for Simple Event Correlator (SEC) Perl process to run on Microsoft Windows operating system as a service. The purpose of running SEC on Microsoft Windows is providing a reliable correlation engine to monitor event logs of the operating system and other software for critical alerts, malicious action, attack patterns and other anomalies, then to interact proactively. SEC is coded using Perl. However Microsoft does not provide a native Perl distribution for Windows. A third party Perl distribution from the available shall be selected, based on features and performance comparison. SEC is not capable of loading Microsoft Windows event logs without the aid of a log collection tool. Miscellaneous applications provide different log formats which require normalization to standardize parsing for extracting information from events. -

Join Query Optimization Techniques for Complex Event Processing Applications
Join Query Optimization Techniques for Complex Event Processing Applications Ilya Kolchinsky Assaf Schuster Technion, Israel Institute of Technology Technion, Israel Institute of Technology Haifa 32000 Israel Haifa 32000 Israel [email protected] [email protected] ABSTRACT Keywords Complex event processing (CEP) is a prominent technology Stream Processing, Complex Event Processing, Lazy Eval- used in many modern applications for monitoring and track- uation, Query Optimization ing events of interest in massive data streams. CEP engines inspect real-time information ows and attempt to detect 1. INTRODUCTION combinations of occurrences matching predened patterns. Complex event processing has become increasingly im- This is done by combining basic data items, also called portant for applications in which arbitrarily complex pat- primitive events, according to a pattern detection plan, terns must be eciently detected over high-speed streams in a manner similar to the execution of multi-join queries of events. Online nance, security monitoring, and fraud in traditional data management systems. Despite this sim- detection are among the many examples. Pattern detection ilarity, little work has been done on utilizing existing join generally consists of collecting primitive events and combin- optimization methods to improve the performance of CEP- ing them into potential (partial) matches using some type based systems. of detection model. As more events are added to a partial In this paper, we provide the rst theoretical and experi- match, a full pattern match is eventually formed and re- mental study of the relationship between these two research ported. Popular CEP mechanisms include nondeterministic areas. We formally prove that the CEP Plan Generation nite automata (NFAs) [5, 18, 51], nite state machines [6, problem is equivalent to the Join Query Plan Generation 45], trees [36], and event processing networks [21, 42]. -

Monitoring the Behaviour of Distributed Systems
Monitoring the Behaviour of Distributed Systems Scarlet Schwiderski Selwyn College University of Cambridge Adissertationsubmittedforthedegreeof Doctor of Philosophy April 1996 Abstract Monitoring the behaviour of computing systems is an important task. In active database systems, a detected system behaviour leads to the triggering of an ECA (event-condition-action) rule. ECA rules are employed for supporting database man- agement system functions as well as external applications. Although distributed database systems are becoming more commonplace, active database research has to date focussed on centralised systems. In distributed debugging systems, a de- tected system behaviour is compared with the expected system behaviour. Differ- ences illustrate erroneous behaviour. In both application areas, system behaviours are specified in terms of events: primitive events represent elementary occurrences and composite events represent complex occurrence patterns. At system runtime, specified primitive and composite events are monitored and event occurrences are detected. However, in active database systems events are monitored in terms of physical time and in distributed debugging systems events are monitored in terms of logical time. The notion of physical time is difficult in distributed systems because of their special characteristics: no global time, network delays, etc. This dissertation is concerned with monitoring the behaviour of distributed sys- tems in terms of physical time, i.e. the syntax, the semantics, the detection, and the implementation of events are considered. The syntax of primitive and composite events is derived from the work of both active database systems and distributed debugging systems; differences and neces- sities are highlighted. The semantics of primitive and composite events establishes when and where an event occurs; the semantics depends largely on the notion of physical time in distributed systems.