Frequency Domain Measurement of Baseband Instrumentation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Slotted Line-SWR
Lab 2: Slotted Line and SWR Meter NAME NAME NAME Introduction: In this lab you will learn how to characterize and use a 50-ohm slotted line, crystal detector, and standing wave ratio (SWR) meter to measure an unknown impedance. The apparatus used is shown below. The slotted line is a (rigid) continuation of the coaxial transmission lines. Its characteristic impedance is 50 ohms. It has a thin slot in its outer conductor, cut along z. A probe rides within (but not touching) the slot to sample the transmission line voltage. The probe can be moved along z to sample the standing wave ratio at different locations. It can also be moved into and out of the slot by means of a micrometer in order to adjust the signal strength. The probe is connected to a crystal (diode) detector that converts the time-varying microwave voltage to a DC value with the help of a low speed modulation envelope (1 kHz) on the microwave signal. The DC voltage is measured using the SWR meter (HP 415D). 1 Using Slotted Line to Measure an Unknown Impedance: The magnitude of the line voltage as a function of position is: + −2 jβ l + j(θ −2β l ) jθ V ()z = V0 1− Γe = V0 1+ Γ e with Γ = Γ e and l the distance from the load towards the generator. Notice that the voltage magnitude has maxima and minima at different locations. + Vmax = V0 (1+ Γ ) when θ − 2β l = π + Vmin = V0 (1− Γ ) when θ − 2β l = 0 V 1+ Γ The SWR is defined as: SWR = max = . -

Department of Electronics and Communication Engineering EC8651 – Transmission Line and Waveguide Unit III - MCQ Bank 1
ChettinadTech Dept of ECE Department of Electronics and Communication Engineering EC8651 – Transmission Line and Waveguide Unit III - MCQ Bank 1. Slotted line is a transmission line configuration that allows the sampling of a) electric field amplitude of a standing wave on a terminated line b) magnetic field amplitude of a standing wave on a terminated line c) voltage used for excitation d) current that is generated by the source Answer: a Explanation: Slotted line allows the sampling of the electric field amplitude of a standing wave on a terminated line. With this device, SWR and the distance of the first voltage minimum from the load can be measured, from this data, load impedance can be found. 2. A slotted line can be used to measure _____ and the distance of _____________ from the load. a) SWR, first voltage minimum b) SWR, first voltage maximum c) characteristic impedance, first voltage minimum d) characteristic impedance, first voltage maximum Answer: a Explanation: With a slotted line, SWR and the distance of the first voltage minimum from the load can be measured, from this data, load impedance can be found. Page 1 EC8651– Transmission Line and Waveguide ChettinadTech Dept of ECE 3. A modern device that replaces a slotted line is: a) Digital CRO b) generators c) network analyzers d) computers Answer: c Explanation: Although slotted lines used to be the principal way of measuring unknown impedance at microwave frequencies, they have largely been superseded by the modern network analyzer in terms of accuracy, versatility and convenience. 4. If the standing wave ratio for a transmission line is 1.4, then the reflection coefficient for the line is: a) 0.16667 b) 1.6667 c) 0.01667 d) 0.96 Answer: a Explanation: ┌= (SWR-1)/ (SWR+1). -

Microwave Impedance Measurements and Standards
NBS MONOGRAPH 82 MICROWAVE IMPEDANCE MEASUREMENTS AND STANDARDS . .5, Y 1 p p R r ' \ Jm*"-^ CCD 'i . y. s. U,BO»WOM t «• U.S. DEPARTMENT OF STANDARDS NATIONAL BUREAU OF STANDARDS THE NATIONAL BUREAU OF STANDARDS The National Bureau of Standards is a principal focal point in the Federal Government for assuring maximum application of the physical and engineering sciences to the advancement of technology in industry and commerce. Its responsibilities include development and main- tenance of the national standards of measurement, and the provisions of means for making measurements consistent with those standards; determination of physical constants and properties of materials; development of methods for testing materials, mechanisms, and struc- tures, and making such tests as may be necessary, particularly for government agencies; cooperation in the establishment of standard practices for incorporation in codes and specifications; advisory service to government agencies on scientific and technical problems; invention and development of devices to serve special needs of the Government; assistance to industry, business, and consumers in the development and acceptance of commercial standards and simplified trade practice recommendations; administration of programs in cooperation with United States business groups and standards organizations for the development of international standards of practice; and maintenance of a clearinghouse for the collection and dissemination of scientific, technical, and engineering information. The scope of the Bureau's activities is suggested in the following listing of its four Institutes and their organizational units. Institute for Basic Standards. Applied Mathematics. Electricity. Metrology. Mechanics. Heat. Atomic Physics. Physical Chem- istry. Laboratory Astrophysics.* Radiation Physics. Radio Stand- ards Laboratory:* Radio Standards Physics; Radio Standards Engineering. -

EECS 117A Demonstration 2 Microwave Measurement Instruments
University of California, Berkeley Spring 2007 EECS 117 Prof. A. Niknejad EECS 117A Demonstration 2 Microwave Measurement Instruments NAME Introduction. Please review the general sinusoidal wave concepts in Secs. 3.1–3.9 of Inan & Inan. Note carefully Section 3.3. In this demonstration you will learn how to use a “50 ohm” slotted line, crystal detector, and standing wave ratio meter to obtain the wavelength λ and voltage standing wave ratio S on a coaxial transmission line. In a later demonstration you will use these techniques to measure and control impedances and reflection coefficients on a microwave transmission system. The apparatus used is shown below. The slotted line is a (rigid) continuation of the coaxial transmission lines “a” connected at each end. It has a thin slot in its outer conductor, cut along z. A probe rides within (but not touching) the slot to sample the transmission line voltage. The probe can be moved along z, and can also be moved into and out of the slot by means of a micrometer. The probe is connected to a crystal (diode) detector that converts the time-varying microwave voltage to dc. The dc voltage is measured using the standing wave ratio (SWR) meter. MICROMETER HP 415D b SWR METER DETECTOR TUNER HP 612 A UHF SIGNAL a TERMINATION GENERATOR a GR SLOTTED LINE POINT (LOAD) Z = 0 Z Suppose a sinusoidal voltage wave j(ωt−βz) v+(t) = Re hV+ e i (1) travels from the RF generator through the slotted line and is incident on a load (resistor, capacitor etc.) at z = 0. -

Unit V Microwave Antennas and Measurements
UNIT V MICROWAVE ANTENNAS AND MEASUREMENTS Horn antenna and its types, micro strip and patch antennas. Network Analyzer, Measurement of VSWR, Frequency and Power, Noise, cavity Q, Impedance, Attenuation, Dielectric Constant and antenna gain. ------------------------------------------------------------------------------------------------------------------------------- DEFINITION: A conductor or group of conductors used either for radiating electromagnetic energy into space or for collecting it from space.or Is a structure which may be described as a metallic object, often a wire or a collection of wires through specific design capable of converting high frequency current into em wave and transmit it into free space at light velocity with high power (kW) besides receiving em wave from free space and convert it into high frequency current at much lower power (mW). Also known as transducer because it acts as coupling devices between microwave circuits and free space and vice versa. Electrical energy from the transmitter is converted into electromagnetic energy by the antenna and radiated into space. On the receiving end, electromagnetic energy is converted into electrical energy by the antenna and fed into the receiver. Basic operation of transmit and receive antennas. Transmission - radiates electromagnetic energy into space Reception - collects electromagnetic energy from space In two-way communication, the same antenna can be used for transmission and reception. Short wavelength produced by high frequency microwave, allows the usage -

SCALAR NETWORK ANALYSIS: an ATTRACTIVE and Cosl-EFFECTIVE TECHNIQUE for TESTING MICROWAVE COMPONENTS
SCALAR NETWORK ANALYSIS: AN ATTRACTIVE AND COSl-EFFECTIVE TECHNIQUE FOR TESTING MICROWAVE COMPONENTS Hugo Vitian Network Measurements Division 1400 Fountain Grove Parkway Santa Rosa, CA 95401 RF ~ Microwave Measurement Symposium and Exhibition Flio- HEWLETT ~~ PACKARD www.HPARCHIVE.com Scalar Network Analysis: an Attractive and Cost-Effective Technique for Testing Microwave Components ABSTRACT Scalar network characterization is an economic alternative to vector network analysis; in particular, in a productive environment where ease-of-use, throughput and low cost are key considerations. However, scalar measurements are not restricted to frequency response measurements on linear networks. Scalar network analyzers are very powerful analysis tools to characterize amplifiers, mixers, modulators, and other components as a function of signal level or control parameter, as well as for cable testing in frequency- and distance-domains. This presentation describes the fundamental measurement concepts and discusses some specific examples. Author: Hugo Vifian, Engineering Section Manager for economy vector network analyzers, HP Network Measurements Division, Santa Rosa, CA. Diplom-Ingenieur and PhD from Swiss Federal Institute of Technology, (ETH). With HP since 1969, projects include HP 8755 frequency response test set, HP 8505 RF vector network analyzer, HP 8756 and 8757 scalar network analyzers. 2 www.HPARCHIVE.com INTRODUCTION TO SCALAR NETWORK MEASUREMENTS Introduction: Even though scalar microwave measurements have been made ever since high frequencies were discovered, they were not really addressed, as such, but INTRODUCTION TO SCALAR rather called power measurements or NETWORK MEASUREMENTS VSWR measurements, etc. It was not until modern network analysis with vector error correction was intro duced that the rather obvious term magnitude or scalar measurements became more popular. -

Microwave Impedance Measurements and Standards
NBS MONOGRAPH 82 MICROWAVE IMPEDANCE MEASUREMENTS AND STANDARDS . .5, Y 1 p p R r ' \ Jm*"-^ CCD 'i . y. s. U,BO»WOM t «• U.S. DEPARTMENT OF STANDARDS NATIONAL BUREAU OF STANDARDS THE NATIONAL BUREAU OF STANDARDS The National Bureau of Standards is a principal focal point in the Federal Government for assuring maximum application of the physical and engineering sciences to the advancement of technology in industry and commerce. Its responsibilities include development and main- tenance of the national standards of measurement, and the provisions of means for making measurements consistent with those standards; determination of physical constants and properties of materials; development of methods for testing materials, mechanisms, and struc- tures, and making such tests as may be necessary, particularly for government agencies; cooperation in the establishment of standard practices for incorporation in codes and specifications; advisory service to government agencies on scientific and technical problems; invention and development of devices to serve special needs of the Government; assistance to industry, business, and consumers in the development and acceptance of commercial standards and simplified trade practice recommendations; administration of programs in cooperation with United States business groups and standards organizations for the development of international standards of practice; and maintenance of a clearinghouse for the collection and dissemination of scientific, technical, and engineering information. The scope of the Bureau's activities is suggested in the following listing of its four Institutes and their organizational units. Institute for Basic Standards. Applied Mathematics. Electricity. Metrology. Mechanics. Heat. Atomic Physics. Physical Chem- istry. Laboratory Astrophysics.* Radiation Physics. Radio Stand- ards Laboratory:* Radio Standards Physics; Radio Standards Engineering. -

A Calibration Free Vector Network Analyzer
Scholars' Mine Masters Theses Student Theses and Dissertations Summer 2013 A calibration free vector network analyzer Arpit Kothari Follow this and additional works at: https://scholarsmine.mst.edu/masters_theses Part of the Electrical and Computer Engineering Commons Department: Recommended Citation Kothari, Arpit, "A calibration free vector network analyzer" (2013). Masters Theses. 7125. https://scholarsmine.mst.edu/masters_theses/7125 This thesis is brought to you by Scholars' Mine, a service of the Missouri S&T Library and Learning Resources. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. i A CALIBRATION FREE VECTOR NETWORK ANALYZER by ARPIT KOTHARI A THESIS Presented to the Faculty of the Graduate School of the MISSOURI UNIVERSITY OF SCIENCE AND TECHNOLOGY In Partial Fulfillment of the Requirements for the Degree MASTER OF SCIENCE IN ELECTRICAL ENGINEERING 2013 Approved by Dr. Reza Zoughi, Advisor Dr. Daryl Beetner Dr. David Pommerenke ii 2013 Arpit Kothari All Rights Reserved iii ABSTRACT Recently, two novel single-port, phase-shifter based vector network analyzer (VNA) systems were developed and tested at X-band (8.2 - 12.4 GHz) and Ka-band (26.4 – 40 GHz), respectively. These systems operate based on electronically moving the standing wave pattern, set up in a waveguide, over a Schottky detector and sample the standing wave voltage for several phase shift values. Once this system is fully characterized, all parameters in the system become known and hence theoretically, no other correction (or calibration) should be required to obtain the reflection coefficient, (Γ), of an unknown load. -

Microwave Variable-Frequency Measurements and Applications
Telecommunications Microwave Microwave Variable-Frequency Measurements and Applications Courseware Sample 85896-F0 Order no.: 85896-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic © Festo Didactic Ltée/Ltd, Quebec, Canada 2010 Internet: www.festo-didactic.com e-mail: [email protected] Printed in Canada All rights reserved ISBN 978-2-89640-425-4 (Printed version) Legal Deposit – Bibliothèque et Archives nationales du Québec, 2010 Legal Deposit – Library and Archives Canada, 2010 The purchaser shall receive a single right of use which is non-exclusive, non-time-limited and limited geographically to use at the purchaser's site/location as follows. The purchaser shall be entitled to use the work to train his/her staff at the purchaser's site/location and shall also be entitled to use parts of the copyright material as the basis for the production of his/her own training documentation for the training of his/her staff at the purchaser's site/location with acknowledgement of source and to make copies for this purpose. In the case of schools/technical colleges, training centers, and universities, the right of use shall also include use by school and college students and trainees at the purchaser's site/location for teaching purposes. The right of use shall in all cases exclude the right to publish the copyright material or to make this available for use on intranet, Internet and LMS platforms and databases such as Moodle, which allow access by a wide variety of users, including those outside of the purchaser's site/location. -

Slotted Line Power Testing of the Directly Coupled Rf Amplifiers
SLOTTED LINE POWER TESTING OF THE DIRECTLY COUPLED RF AMPLIFIERS B. Bojović, I. Trajić, P. Beličev, Laboratory of Physics, Vinča Institute of Nuclear Sciences, Belgrade, Serbia and Montenegro Abstract via a sliding short while fine tuning is performed by a The direct coupling of radiofrequency (RF) power trimming loop. Both amplifier chains begin with amplifiers to their cavities has many advantages frequency synthesizer and consist of tree amplifiers. The compared to the 50 Ohm feeder line coupling. The main first stage, a predriver amplifier is a commercial disadvantage of the direct coupling is the fact that its wideband amplifier MARCONI H1000, modified to have power testing needs to be done with the amplifier coupled an operating range up to 31 MHz, and to be driven by a to the cavity because a 50 Ohm water cooled resistor can frequency synthesizer. The second and third stages are not be used for that purpose due to a lack of the custom made driver and power amplifiers in cascode appropriate impedance matching. We found a solution to configuration. The driver amplifiers are realized with a 20 this problem in using a longitudinally slotted coaxial line kW tetrodes in the grounded cathode configuration and short-circuiting the amplifier cabinet. The slotted line the power amplifiers are realized with 75 kW tetrodes in accommodates a 50 Ohm water cooled resistor in parallel the grounded grid configuration [3]. The power amplifier to the short-circuiting plate, enabling one to vary the is directly coupled to the resonator via coupling line and quality factor of the amplifier cabinet by moving the coupling loop (Fig. -
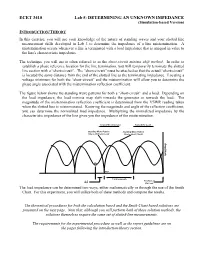
ECET 3410 Lab 5: DETERMINING an UNKNOWN IMPEDANCE (Simulation-Based Version)
ECET 3410 Lab 5: DETERMINING AN UNKNOWN IMPEDANCE (Simulation-based Version) INTRODUCTION/THEORY In this exercise, you will use your knowledge of the nature of standing waves and your slotted line measurement skills developed in Lab 3 to determine the impedance of a line mistermination. A mistermination occurs whenever a line is terminated with a load impedance that is unequal in value to the line's characteristic impedance. The technique you will use is often referred to as the short-circuit minima shift method. In order to establish a phase reference location for the line termination, you will temporarily terminate the slotted line section with a “short-circuit”. The “short-circuit” must be attached so that the actual “short-circuit” is located the same distance from the end of the slotted line as the terminating impedance. Locating a voltage minimum for both the “short-circuit” and the mistermination will allow you to determine the phase angle associated with the mistermination reflection coefficient. The figure below shows the standing wave patterns for both a “short-circuit” and a load. Depending on the load impedance, the load minima may shift towards the generator or towards the load. The magnitude of the mistermination reflection coefficient is determined from the VSWR reading taken when the slotted line is misterminated. Knowing the magnitude and angle of the reflection coefficient, you can determine the normalized load impedance. Multiplying the normalized impedance by the characteristic impedance of the line gives you the impedance of the mistermination. Toward the Generator Toward the Load Standing Wave Pattern Standing Wave Pattern Due to Unknown Load Due to Short Circuit Amplitude Min. -

The Slotted Measuring Line Sampling the Field in Front of a Short-Circuit Plate and a Waveguide Termination
MTS 7.4.4 The Measuring Line The slotted measuring line Sampling the field in front of a short-circuit plate and a waveguide termination Principles Various line types for electromagnetic waves and their technical function Lines fulfill various functions in radio fre- quency technology: (a) They serve in the transmission of radio fre- quency signals between remote locations. Examples: radio link between the transmit- ter and a remote antenna system, broadband cable for signal distribution of a satellite re- ceiver system to the individual subscribers and underwater cables. Transmission lines and directional radio links in free space are frequently considered potential alternatives in this function as a medium for communi- cations transmission (b) They also serve as circuit elements (in- stead of capacitors and inductors) and in- terconnecting lines for the realization of passive microwave circuits (e.g. transmis- sion-line filters). In general, transmission lines can be consid- ered as structures for guiding electromagnetic waves. For this function a multitude of various transmission line types are suitable. Fig. 5.1: Various line types for electromagnetic waves (1 = metal conductor, 2 = isolator). The coaxial and two-wire line depicted in Fig. Numbering from left to right. 5.1a) guides transverse electromagnetic waves (a) Coaxial and two-wire lines (TEM waves) and can also be used for any ar- (b) Planar line structures: Microstrip line, bitrarily low frequency. coplanar line, slotted line In other transmission line types, however, the (c) Waveguide: Rectangular, circular and wave propagation is dependent on the condi- ridged waveguides tion that the cross-sectional dimensions of the (d) Dielectric waveguides: Round and rectangular-shaped surface waveguide; line are at least about as large as a half free- optical waveguide λ space wavelength ( 0/2).