DOCSLIB.ORG

Credit Default Swaptions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Credit Default Swaptions Credit Default Swaptions ALAN L. TUCKER AND JASON Z. WEI ALAN L. TUCKER mong the credit derivatives traded I. PRODUCT DESCRIPTION is an associate professor of since 1991, credit default swaps finance in the Lubin School (CDS) account for the vast majority We describe CDS swaptions using an of Business at Pace University of trading. Like interest rate swap- example. Assume that all counterparties in New York City, A (dealers and buy side) are AA-rated, which [email protected] tions in the interest rate marketplace, credit default swaptions represent a potentially impor- could be through credit enhancements such JASON Z. WEI tant derivative product for credit markets, as collateral, midmarket, or netting agreements. is an associate professor A CDS that is cancelabie includes an Assume the CDS that underlies the of finance in the Rotman embedded credit default swaption, A cance- swaption has a three-year maturity, semian- School of Management at lable long CDS position (where long means nual payment dates, and a swap rate (the strike the University ofToronto rate on the swaption) of 150 basis points (bp). in Toronto, Ontario, that the CDS trader is paying a fixed swap rate and is thus the buyer of credit protection) is a The strike rate assumes semiannual com- package of a straight (non-cancelable) long pounding—the same periodicity (or tenor) of CDS plus a put-style CDS swaption—an the CDS, The credit default swap underlying option to enter a CDS short and thus close the reference credit asset is a BB-rated ten- the outstanding long position, A cancelable year 8% coupon bond with $100 lnillion par. short CDS represents a combination ofa short The CDS swaption is a call, European-style, position in a straight CDS plus a call-style CDS with a maturity of six months. Thus the CDS swaption,' swaption owner has the right, in six months, to enter the underlying CDS long, that is, To the extent that a CDS is cancelable— paying 150 bp. and most are in practice—ignoring the value of the embedded CDS swaption can lead to Suppose that in six months, when the pricing errors and thus arbitrage opportuni- swaption matures, the bid-offer swap rates on ties. We believe that methods used to establish newly minted three-year credit default swaps initial swap rates on cancelable CDS, as well (with semiannual tenors)—on the same refer- as methods used to value seasoned CDS that ence credit asset (or pari passu asset)—are 200 are cancelable, typically ignore the embedded bp by 220 bp,^ The underlying bond has thus swaption to terminate the position, so these exhibited credit deterioration, perhaps having CDS may be mispriced,^ been downgraded to a weak single B, The call Our purposes are threefold: to describe swaption is exercised, meaning that its owner CDS swaptions; to illustrate some of their can now long the same swap payingjust 150 bp. applications; and, most important, to present By engaging in a reversing trade (enter- accessible valuation models. ing a short CDS), the swaption owner locks in an annuity of 50 bp (the bid of 200 bp less 88 CREDIT DEFAULT SWAPTIONS JUNE 2005 the strike rate of 150 bp) on $50 million for the next six CDS does not eliminate the need for the call swaption semiannual periods. This annuity is present-valued (mon- owner to exercise in the event of default ofthe reference etized) at the interest rate swap midrate on a new three- credit asset. Finally, these circumstances do not affect can- year semi-annual (s,a,) dollar-LIBOR swap since both celable CDS, A default-triggering event terminates the CDS counterparties are AA-rated, and therefore the embedded option to cancel the CDS, lfthe swaption is a put and at expiration new CDS Besides plain vanilla CDS swaptions—whether rates are 100 bp by 110 bp (perhaps because the bond is American, Bermudan, European, calls, puts, outright, or now a weak single A), the payoff to the CDS swaption embedded in cancelable CDS—there are a variety of more would be the present value (again, discounted at the three- exotic CDS swaptions, such as swaptions written on binary year interest rate swap midrate) of six annuity payments and basket CDS, or barrier CDS swaptions. It will be of $50 million times 40 bp (the strike rate of 150 bp less interesting to watch changes in the market for CDS swap- the offer of 110 bp),-* tions as the market for credit derivatives in general con- CDS swaptions that are traded outright are likely to tinues to grow in size and innovation, be European, but a cancelable CDS will entail either an American or Bermudan swaption. For example, consider a II. PRODUCT APPLICATION long CDS giving the buyer of credit protection the option to terminate the swap every six months. Assume the under- To illustrate the use of CDS swaptions, we consider lying reference credit asset is unique and illiquid, and has three product applications: to reduce a bank's regulatory no pari passu substitutes. Then this CDS represents a package capital; to create a synthetic credit-linked note; and to ofa straight CDS plus a potentially valuable Bermudan put create a synthetic collateralized debt obligation. swaption—the ability to short the CDS, at six-month inter- vals, thus closing the original long position, Reducing Bank Regulatory Capital lfthe reference credit asset (our 8% coupon bond) has a default-triggering event (such as a missed coupon date) Suppose a bank is carrying so many commercial before the six-month maturity ofthe swaption, the CDS loans as to compromise its regulatory capital. The bank would be terminated by physical or cash settlement, which cannot sell all the loans because most are not assignable; means we have a CDS swaption with no underlying, lfthe it needs to reduce its regulatory capital requirements. CDS swaption is a put, the issue is moot; the put swaption The bank can sell one loan and use the proceeds to owner would not want to exercise, because the credit spread purchase a call credit default swaption whose underlying on the defaulted bond would presumably explode to some- reference credit asset is a portfolio ofthe remaining loans thing well above the original (150 bp) strike rate. (or a highly correlated basket of them). By purchasing this If it is a call swaption, the owner would want to exer- basket CDS call swaption, the bank should obtain regu- cise. The call owner therefore needs a mechanism to cap- latory capital relief much like being long a basket CDS, ture value, European-style CDS call swaptions permit early The principal advantage of buying the CDS call exercise in the event of a default-triggering event for the swaption (versus entering a long position in a basket CDS) reference credit asset before maturity ofthe CDS swaption,' is the returns earned on the loans should their credit lfthe CDS call swaption is exercised early because of quality improve. The principal disadvantage ofthe swap- default of the reference credit asset, the swaption owner tion is its cost. ought to be required to make a payment to the writer. Such a payment represents a type of premium accrual on a default Creating a Synthetic Credit-Linked Note insurance policy written on the reference credit asset. In our illustration, if at inception of the swaption there is a Suppose a hedge fund buys a four-year floating-rate six-month bond insurance policy costing 10 bp of face value note issued by a highly rated bank sponsor. The note pays that pays the difference between the face value and the s,a, dollar-LIBOR plus 5 bp. The fund manager can recovery value of the bond, then, assuming the reference enhance the coupon to s,a, $LIBOR plus 45 bp if she credit asset defaults midway through the life ofthe swap- agrees to bear the default risk associated with an alto- tion, the CDS call swaption owner (or its bond insurance gether different bond (in addition to the credit risk ofthe company) would be required to pay 5 bp of $100 million. note she is buying). This is a common credit-linked note Note that a pari passu provision on the underlying (representing a way dealers lay off their credit risk from JUNE 2005 THE JOURNAL OF FIXED INCOME 89 engaging in short CDS positions). European CDS Swaption Pricing Instead, the manager can effectively enhance the coupon on the note by writing a put CDS swaption on If the forward credit default swap midrate is log- the same/second bond. By purchasing the floating-rate normal, European CDS swaptions can be priced using a note and writing the put CDS swaption, the hedge fund straightforward modification of Black's [1976] model,^ manager is long a synthetic credit-linked note. That is, the CDS swaption can be priced using a model that prices interest rate swaptions. The notation is as follows: Creating a Synthetic Collateralized Debt Obligation Rg = relevant forward CDS swap rate, expressed Suppose an asset manager wants to create a synthetic with compounding of m periods per year, collateralized debt obligation (CDO), so he issues or spon- at time 0; sors a $200 million CDO (through a special-purpose vehicle) Rj, = strike rate on the CDS swaption, also expressed with four debt tranches and one equity tranche, $175 mil- with compounding of m periods per year; lion represents the debt tranches and $25 million represents T = maturity ofthe CDS swaption; the equity tranche, which the sponsor keeps. The $200 mil- O = standard deviation ofthe change in the nat- lion is then invested in high-quality agency securities.
Load more

Recommended publications
  • Guarantee and Embedded Options
    Guarantee and embedded options Gary Finkelstein, Emma McWilliam, Paul de Beus, Rob van Leijenhorst, Steve Nagle Lotte Maas, Jiajia Cui Contact address: Contact address: Ernst & Young Life Actuarial Practice Ernst & Young Actuaries Rolls Buildings Euclideslaan 1 Fetter Lane 3584 BL Utrecht EC4A 1NH P.O. Box 3053 London 3502 GB Utrecht UNITED KINGDOM THE NETHERLANDS Tel: +44-20-7951-0176 Tel.: +31 –30-259-2224 Fax: +44-20-7951-8010 Fax: +31 –30-259-2118 email: [email protected] Email: [email protected] This Version: 27 June, 2003 Abstract Recent economic events, the changing attitude of regulators, and a possible global change in reporting to shareholders have put the options and guarantees included in today’s insurance products at the top of the list of management’s concerns. Indeed, many senior insurance executives around the world have indicated that they regard the identification, pricing, management, and valuation of guarantees and options embedded in insurance contracts as the most important and difficult financial challenge they face. On too many occasions over the years, insurance company executives have been surprised by the financial costs of embedded guarantees and options that were not properly understood. An understanding of options and guarantees has become essential to the sound financial management of insurance companies. This paper provides an introduction to the valuation of guarantees and options embedded in life insurance products. It explains the link between investment guarantees and embedded options, and consequently their measurement on a market-value basis. It also explores the implications of guarantees and options for asset and liability valuation, product pricing, and managing balance-sheet volatility.
    [Show full text]
  • Convertible Bond Investing Brochure (PDF)
    Convertible bond investing Invesco’s Convertible Securities Strategy 1 Introduction to convertible bonds A primer Convertible securities provide investors the opportunity to participate in the upside of stock markets while also offering potential downside protection. Because convertibles possess both stock- and bond-like attributes, they may be particularly useful in minimizing risk in a portfolio. The following is an introduction to convertibles, how they exhibit characteristics of both stocks and bonds, and where convertibles may fit in a diversified portfolio. Reasons for investing in convertibles Through their combination of stock and bond characteristics, convertibles may offer the following potential advantages over traditional stock and bond instruments: • Yield advantage over stocks • More exposure to market gains than market losses • Historically attractive risk-adjusted returns • Better risk-return profile • Lower interest rate risk Introduction to convertibles A convertible bond is a corporate bond that has the added feature of being convertible into a fixed number of shares of common stock. As a hybrid security, convertibles have the potential to offer equity-like returns due to their stock component with potentially less volatility due to their bond-like features. Convertibles are also higher in the capital structure than common stock, which means that companies must fulfill their obligations to convertible bondholders before stockholders. It is important to note that convertibles are subject to interest rate and credit risks that are applicable to traditional bonds. Simplified convertible structure Bond Call option Convertible Source: BofA Merrill Lynch Convertible Research. The bond feature of these securities comes from their stated interest rate and claim to principal.
    [Show full text]
  • VALUATION of CALLABLE BONDS: the SALOMON BROTHERS APPROACH Fernando Daniel Rubio Fernández
    VALUATION OF CALLABLE BONDS: THE SALOMON BROTHERS APPROACH Fernando Daniel Rubio Fernández VALUATION OF CALLABLE BONDS: THE SALOMON BROTHERS APPROACH FERNANDO RUBIO1 Director FERNCAPITAL S.A. and Invited Professor at the Graduated Business School Universidad de Valparaíso, Chile. Pasaje La Paz 1302, Viña del Mar, Chile. Phone (56) (32) 507507 EXTRACT This paper explain, analyze and apply in an example the original paper developed by Kopprasch, Boyce, Koenigsberg, Tatevossian, and Yampol (1987) from The Salomon Brothers Inc. Bond Portfolio Analysis Group. Please, be aware. This paper is for educational issues only. There is a Spanish version in EconWPA. JEL Classification: G10, G15, G21, G32. Keywords: Salomon Brothers, bond portfolio, duration and convexity, effective duration, valuation, callable and non callable bond. Originally developed January, 1999 Originally published October, 2004 This update July, 2005 1 This paper was made while I was assisting to the Doctoral Programme in Financial Economics, Universidad Autónoma de Madrid, Spain. Comments and suggestions will be appreciated. Please, send them by e-mail to [email protected] [email protected] 1 VALUATION OF CALLABLE BONDS: THE SALOMON BROTHERS APPROACH Fernando Daniel Rubio Fernández VALUATION OF CALLABLE BONDS: THE SALOMON BROTHERS APPROACH By Professor Dr. © Fernando Rubio 1 DURATION AND CONVEXITY FOR NORMAL (NO CALLABLE) BONDS Bonds are fixed income investments that have a fixed interest rate or coupon, payable on the principal amount. All fixed income investments are evidence of indebtedness which represent a loan or debt between the issuer and the owner or holder of the security. The value of any bond is the present value of its expected cash flows.
    [Show full text]
  • Credit Derivatives Handbook
    08 February 2007 Fixed Income Research http://www.credit-suisse.com/researchandanalytics Credit Derivatives Handbook Credit Strategy Contributors Ira Jersey +1 212 325 4674 [email protected] Alex Makedon +1 212 538 8340 [email protected] David Lee +1 212 325 6693 [email protected] This is the second edition of our Credit Derivatives Handbook. With the continuous growth of the derivatives market and new participants entering daily, the Handbook has become one of our most requested publications. Our goal is to make this publication as useful and as user friendly as possible, with information to analyze instruments and unique situations arising from market action. Since we first published the Handbook, new innovations have been developed in the credit derivatives market that have gone hand in hand with its exponential growth. New information included in this edition includes CDS Orphaning, Cash Settlement of Single-Name CDS, Variance Swaps, and more. We have broken the information into several convenient sections entitled "Credit Default Swap Products and Evaluation”, “Credit Default Swaptions and Instruments with Optionality”, “Capital Structure Arbitrage”, and “Structure Products: Baskets and Index Tranches.” We hope this publication is useful for those with various levels of experience ranging from novices to long-time practitioners, and we welcome feedback on any topics of interest. FOR IMPORTANT DISCLOSURE INFORMATION relating to analyst certification, the Firm’s rating system, and potential conflicts
    [Show full text]
  • Sweet Spot Investing with Convertible Bonds by Jim Buckham CFA, Portfolio Manager
    20 William Street, Wellesley, MA 02481 781-416-4000 Sweet Spot Investing with Convertible Bonds By Jim Buckham CFA, Portfolio Manager Convertible bonds are sometimes considered the "Swiss Army knife" of financial products because they can provide investors with principal protection (barring default), income, and equity-like returns. The combination of a corporate bond with a call option can provide investors with asymmetrical returns: when stocks rise, the returns are more equity-like; when stocks fall, the returns are more bond-like. A convertible bond’s value is the potential to increase returns in a fixed income portfolio and dampen volatility in an equity portfolio. The secret to enjoying these benefits is investing in what convertible bond managers refer to as the "sweet spot." This means investing in convertible bonds trading close to par that have a balanced profile. Here at Wellesley Asset Management, we look to invest in the sweet spot of convertible bonds to unlock the many benefits this financial instrument can provide to investors. Options traders use the term "delta" to describe the change in price of an option in relation to the change in price of the underlying security. For example, if a call option in Apple, Inc. is trading on a 50 delta (the delta is the ratio of the change in price of an option to the change in price of the underlying asset) and Apple stock moves favorably by $1.00, then the option’s value will increase by $.50. Similarly, the convertible market uses delta to compare changes in stock prices to changes in convertible bond prices.
    [Show full text]
  • Collateralized Mortgage Obligations: Risk in the Derivatives Market
    Collateralized Mortgage Obligations: Risk in the Derivatives Market by Bronwynne Tuss A Thesis Presented a Bachelor's Degree in Business Administration with Distinction The Ohio State University Max M. Fisher College of Business May 26,1995 Examining Professor Milligan Professor Ray Professor Richard Murdock This thesis is dedicated to two individuals whose generous assistance this work possible: Professor Richard Murdock and my Carl Tuss. Thank you for inspiring my confidence. Table of Contents Introduction p.1 Growth of Derivatives Market p.3 Mounting Concern Over p.6 The Nature and of Collateralized Mortgage Obligations p.B Analysis Underlying Mortgage Collateral p.13 Analysis of Risk Factors Associated with Collateralized Mortgage Obligations p.1S Case Studies p.26 Issues p.34 Conclusion Exhibits Introduction Derivative instruments bear a striking resemblance to a double-edged sword. While some investors made fortunes using these financial tools, others have experienced economic ruin. As a result of some surprisingly large losses incurred by a wide variety of investors, many companies are reconsidering their risk management methods. Accordingly, the dollar volume of derivative sales declined by 94% for the first quarter of 1995 (Norris 1995). This decline in derivative sales is due to both big losses and the bad publicity surrounding derivatives litigation (Norris 1995). Small public institutions, as well as companies with millions of dollars in assets, became losers. For example, Orange County, California lost $2 billion in 1994 using derivatives (Zuckerman 1995). In the same year, Proctor & Gamble, which employs a risk management committee, lost $157 million (Loomis 1994). As a result of such losses, many lawsuits have foJlowed.
    [Show full text]
  • Derivative Instruments and Hedging Activities
    www.pwc.com 2015 Derivative instruments and hedging activities www.pwc.com Derivative instruments and hedging activities 2013 Second edition, July 2015 Copyright © 2013-2015 PricewaterhouseCoopers LLP, a Delaware limited liability partnership. All rights reserved. PwC refers to the United States member firm, and may sometimes refer to the PwC network. Each member firm is a separate legal entity. Please see www.pwc.com/structure for further details. This publication has been prepared for general information on matters of interest only, and does not constitute professional advice on facts and circumstances specific to any person or entity. You should not act upon the information contained in this publication without obtaining specific professional advice. No representation or warranty (express or implied) is given as to the accuracy or completeness of the information contained in this publication. The information contained in this material was not intended or written to be used, and cannot be used, for purposes of avoiding penalties or sanctions imposed by any government or other regulatory body. PricewaterhouseCoopers LLP, its members, employees and agents shall not be responsible for any loss sustained by any person or entity who relies on this publication. The content of this publication is based on information available as of March 31, 2013. Accordingly, certain aspects of this publication may be superseded as new guidance or interpretations emerge. Financial statement preparers and other users of this publication are therefore cautioned to stay abreast of and carefully evaluate subsequent authoritative and interpretative guidance that is issued. This publication has been updated to reflect new and updated authoritative and interpretative guidance since the 2012 edition.
    [Show full text]
  • Effects of Negative Interest Rates on Floating Rate Loans and Bonds Analysis of Legal and Financial Profiles
    Quaderni giuridici (Legal research papers) Effects of negative interest rates on floating rate loans and bonds Analysis of legal and financial profiles S. Alvaro, A. Gentili, C. Mottura 14 November 2017 L’attività di ricerca e analisi della Consob intende promuovere la riflessione e stimolare il dibattito su temi relativi all’economia e alla regolamentazione del sistema finanziario. I Quaderni di finanza accolgono lavori di ricerca volti a contribuire al dibattito accade- mico su questioni di economia e finanza. Le opinioni espresse nei lavori sono attribuibili esclusivamente agli autori e non rappresentano posizioni ufficiali della Consob, né impe- gnano in alcun modo la responsabilità dell’Istituto. Nel citare i lavori della collana, non è pertanto corretto attribuire le argomentazioni ivi espresse alla Consob o ai suoi Vertici. I Discussion papers ospitano analisi di carattere generale sulle dinamiche del sistema finanziario rilevanti per l’attività istituzionale. I Quaderni giuridici accolgono lavori di ricerca volti a contribuire al dibattito accademi- co su questioni di diritto. Le opinioni espresse nei lavori sono attribuibili esclusivamente agli autori e non rappresentano posizioni ufficiali della Consob, né impegnano in alcun modo la responsabilità dell’Istituto. Nel citare i lavori della collana, non è pertanto corret- to attribuire le argomentazioni ivi espresse alla Consob o ai suoi Vertici. I Position papers, curati dalla Consob anche in collaborazione con altre istituzioni, illustrano ipotesi di modifiche del quadro regolamentare o degli approcci di vigilanza e ricognizioni di aspetti applicativi della normativa vigente. Comitato di Redazione Simone Alvaro (coordinatore), Doina D’Eramo, Giorgio Gasparri, Giovanni Mollo Segreteria di Redazione Eugenia Della Libera, Walter Palmeri, Fabio Vasselli Progetto Grafico Studio Ruggieri Poggi Stampa e allestimento Marchesi Grafiche Editoriali Spa (Roma) www.marchesigrafiche.it Consob 00198 Roma – Via G.B.
    [Show full text]
  • Convertible Bonds: a Strategic Allocation
    Insights Fixed Income Convertible Bonds: November 2020 A Strategic Allocation Shankar Abburu • Even a small strategic allocation to convertible bonds Quantitative Research & Analysis has historically improved the risk-return profile for EMEA & APAC, SPDR ETF investment portfolios, both multi-asset and pure fixed Model Portfolio Solutions State Street Global Advisors income portfolios. Daniel Ung, CFA, • Convertible bonds can give rise to a favourably CAIA, FRM Head of Quantitative asymmetric risk profile, offering the possibility of Research & Analysis capturing more upside than downside. EMEA & APAC, SPDR ETF Model Portfolio Solutions State Street Global Advisors • Convertible bonds may be capital efficient as they can offer exposure to equities with a lower Solvency II capital charge. Overview In this paper, we examine how to incorporate convertible bonds into an investment portfolio from a strategic asset allocation standpoint. To this end, we explain the need for selecting the right convertible bond index exposure and also highlight how convertible bonds may be an option for insurers seeking equity-like returns but wishing to lower Solvency II capital requirements (SCR). To support our views, we conduct a risk attribution analysis for including convertible bonds in a multi-asset portfolio. How to Incorporate Convertible bonds used as part of a strategic (core) allocation within investment portfolios have Convertible Bonds in the potential to improve risk-return efficiency as well as risk capital efficiency, in particular for a Portfolio Context insurers. Convertible bonds not only can help mitigate drawdowns in multi-asset portfolios but also capture more equity upside than downside, by virtue of their asymmetrical risk profile, in conventional fixed income portfolios.
    [Show full text]
  • Fabozzi Course.Pdf
    Asset Valuation Debt Investments: Analysis and Valuation Joel M. Shulman, Ph.D, CFA Study Session # 15 – Level I CFA CANDIDATE READINGS: Fixed Income Analysis for the Chartered Financial Analyst Program: Level I and II Readings, Frank J. Fabozzi (Frank J. Fabozzi Associates, 2000) “Introduction to the Valuation of Fixed Income Securities,” Ch. 5 “Yield Measures, Spot Rates, and Forward Rates,” Ch. 6 “Introduction to Measurement of Interest Rate Risk,” Ch. 7 © 2002 Shulman Review/The Princeton Review Fixed Income Valuation 2 Learning Outcome Statements Introduction to the Valuation of Fixed Income Securities Chapter 5, Fabozzi The candidate should be able to a) Describe the fundamental principles of bond valuation; b) Explain the three steps in the valuation process; c) Explain what is meant by a bond’s cash flow; d) Discuss the difficulties of estimating the expected cash flows for some types of bonds and identify the bonds for which estimating the expected cash flows is difficult; e) Compute the value of a bond, given the expected cash flows and the appropriate discount rates; f) Explain how the value of a bond changes if the discount rate increases or decreases and compute the change in value that is attributable to the rate change; g) Explain how the price of a bond changes as the bond approaches its maturity date and compute the change in value that is attributable to the passage of time; h) Compute the value of a zero-coupon bond; i) Compute the dirty price of a bond, accrued interest, and clean price of a bond that is between coupon
    [Show full text]
  • Fixed Income 3 Level II 2020
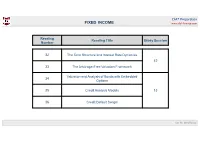
    CFA® Preparation FIXED INCOME www.dbf-finance.com Reading Reading Title Study Session Number 32 The Term Structure and Interest Rate Dynamics 12 33 The Arbitrage-Free Valuation Framework Valuation and Analysis of Bonds with Embedded 34 Options 35 Credit Analysis Models 13 36 Credit Default Swaps Luis M. de Alfonso CFA® Preparation FIXED INCOME www.dbf-finance.com Valuation and Analysis of Bonds with Embedded Options Study Session 13 Reading Number 34 Luis M. de Alfonso CFA® Preparation FI – Valuation and Analysis of Bonds with Embedded Options www.dbf-finance.com LOS 34.a: Describe fixed-income securities withembedded options Ø Embedded options in a bond allow an issuer to (1) manage interest rate risk and/or (2) issue the bonds at an attractive coupon rate Ø Embedded options can be (a) Simple options or (b) Complex options a) Simple options a.1) Callable bonds • Gives the issuer the option to call back the bond • Investor is short the call option a.2) Putable bonds • Allow the investor to put (sell) the bond back to the issuer prior to maturity • Investor is long the put option b) Complex options b.1) Estate put • Allows the heirs of an investor to sell the bond upon the death of the investor b.2) Sinking Fund bonds • Require the issuerto set aside funds periodically to retire the bond • This provision reduces the credit risk Luis M. de Alfonso CFA® Preparation FI – Valuation and Analysis of Bonds with Embedded Options www.dbf-finance.com LOS 34.b: Explain the relationships between the values of a callable or putable bond, the underlying
    [Show full text]
  • Option Adjusted Spread Model PRIME 3.0
    Option Adjusted Spread Model PRIME 3.0 Document: FCA 2276-1A (1) April 2004 Notices This edition This edition FCA 2276-1A (1) applies to application component PRIME 3.0 of FRONT CAPITAL SYSTEMS ARENA (hereafter referred to as FRONT ARENA) and to all subsequent releases of this component until otherwise indicated in new editions. Legal Information in this document is subject to change without notice and does not represent a commitment on the part of Front Capital Systems AB. © Copyright Front Capital Systems AB, 2003. All rights reserved. This material contains proprietary and copyrighted information, software and accompanying documentation belonging to Front Capital Systems AB that is protected by domestic laws and international conventions. Except as stated herein or in the Software License and Service Agreement, none of the information, software or accompanying documentation may be reproduced, distributed, displayed, posted or transmitted by any means, electronic or manual, for any purpose, without the express written permission of Front Capital Systems AB. FRONT CAPITAL SYSTEMS; FRONT CAPITAL SYSTEMS ARENA, FRONT ARENA, and all related logos are the registered trademarks of Front Capital Systems AB. Front Capital Systems AB recognises the registered trademarks of other suppliers mentioned in this document including Reuters and Sun Microsystems. UNIX is a registered trademark in the United States and other countries, licensed exclusively through X/Open Company Limited. Microsoft, Windows, Windows NT are registered trademarks of Microsoft Corporation. Other company, product, and service names may be trademarks or service marks of others. Supplementary legal notice Any information expressed in this document regarding standard practice or conventions in financial markets or in the administration or functioning of banks is included to provide context to information provided about our products and services and thereby clarify how these products and services function.
    [Show full text]