Online Appendix for Misallocation in the Market for Inputs: Enforcement and the Organization of Production
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ecommittee Newsletter November 2020
November 2020 Newsletter e-Committee, Supreme Court of India NORTH EAST GETS THE FIRST VIRTUAL COURT AT ASSAM. The 1st Virtual Court of North-East august presence of Hon’ble Dr India was inaugurated for the State Justice D.Y. Chandrachud, Judge – of Assam, on 12th November 2020, cum- Chairperson, e-Committee, by Hon’ble Chief Minister of Assam, Supreme Court of India, Hon’ble Mr Sri Sarbananda Sonowal in the Justice Hrishikesh Roy, Judge, e-Committee Newsletter, November 2020 2 Supreme Court of India, Hon’ble Mr thus freeing up judicial manpower for Justice N. Kotiswar Singh, Chief essential judicial functions. Justice (Acting), Gauhati High Court, In this regard, Gauhati High Court, Hon’ble Chief Justices & Judges of under the aegis of the e-Committee, Various High Courts. Mr Barun Mitra the Hon’ble Supreme Court of India, Secretary, Department of Justice, Mr has taken up the project of the Justice R.C. Chavan, Vice- setting of Virtual Courts for traffic Chairperson, e-Committee, violations. Gauhati High Court has Supreme Court of India, Dr Neeta taken a proactive role in Verma, Director General, National implementing e-Challan by the State Informatics Centre, Government of Police for enabling the Virtual India, CPCs of Various High Courts, Courts. District Administrations, Police The High Court’s e-Courts Division Officials under the Jurisdiction of the made a presentation on the Gauhati High Court joined the implemented e-Challans for the function virtually. Police Authorities and the ease of Virtual courts provide a convenient services offered by the Virtual Courts option for citizens to pay traffic fines for the Citizens. -

Newsletter E-Committee, Supreme Court of India
March, 2021 Newsletter e-Committee, Supreme Court of India Table of Contents Standard Operating Procedure (SOP) For Digital Preservation ................................................ 3 eCommittee Trains 4006 Advocate Master Trainers ................................................................ 4 Accessible Legal Eco System-Coordination Meeting with the CPCs of High Court. .................... 6 The First Virtual Court Of Chhattisgarh Inaugurated ............................................................... 7 High Court Of Meghalaya Launches Mobile Application. ......................................................... 8 ICJS Related E-Prosecution Software Training held By Meghalaya High Court ....................... 9 Justice Clocks Made Functional At Jodhpur & Jaipur Bench of Rajasthan High Court . ...........10 The Launch Of Mobile Application And Pagination Programme At HC Of Madhya Pradesh . ..11 Telangana State Judicial Academy Launches Official Website www.tsja.gov.in .....................13 NStep Training Programme At High Court of Madras .............................................................14 Coordination Meeting For Effective Implementation of E-Courts Project At HC Of Kerala. ......15 Know the Best Practices Of High Court Of Delhi & High Court of Gauhati ...............................16 High Court Of Himachal Pradesh Adds New Functionality In Display Board Software. ............17 Advocate Master Trainer Programme-Coordination meeting with State Judicial Academies. 18 e-Courts Awareness Programme Through National -

WP(C) No. 127/2015 BEFORE the HON
WP(C) No. 127/2015 BEFORE THE HON’BLE MR JUSTICE UMA NATH SINGH, CHIEF JUSTICE HON’BLE MR JUSTICE T NANDAKUMAR SINGH & HON’BLE MR JUSTICE S R SEN 27.05.2015 We have heard learned Advocate General, Meghalaya and the Director General of Police, Mr Mehta, and perused the writ petition. Registrar General of this Court has put up an office note on the basis of press clippings and informations regarding the impact of „Bandh‟ on the presence of Court Staff and also on essential services, like hospitals and medical shops etc. As per administrative order of the even date, the Office Report has been directed to be registered as WP(C)No. 127 of 2015. It appears from the averment of Office note/writ petition that there are 71 indoor patients and 248 OPD patients in various hospitals of Shillong. It also appears that 20% of High Court staff and lawyers practicing in the District Court of West Jaintia Hills District, Jowai, are absent on account of calling of bandh. The District Court, West Jaintia Hills District could not function because of absence of lawyers. The bandh has been called by the organization called “Hynniewtrep National Liberation Council” (for short „HNLC‟) which is said to have been banned as unlawful association for a further period of five years by the order dated 25.05.2015 passed by the Unlawful Activities (Prevention) Tribunal, Delhi. It has become a regular feature in the day to day life of Meghalaya, particularly, the City of Shillong to observe bandh even on a 2 hoax call in the name of this organization said to be operating from the territory of Bangladesh with a limited and dwindling cadre. -

The High Court of Meghalaya at Shillong
THE HIGH COURT OF MEGHALAYA AT SHILLONG No.HCM.III46I 2016 I Prclj DL.Shg,Lhe __Marcll.,2Vl0 SHORT TERM TENDER Sealed Quotations affixing non-refundable Court fee stamp of Rs. 201 Rupees twenty ) only are invited for printing of High Court of Meghalaya, Telephone Directory-2016 size 12 em X 9 em from intending Firm s (Govt. Registered).The details of th e Quotation are available on our website http: //m eghalavahighcourt.nic.in . The quotations in sealed cover address to REGISTRAR GENERAL, High Court of Meghalaya, Shillong - 793001 must reach the office of the undersigned by 1.00 PM on or before 29.03.201q and the quotations will be opened at 2 .00 PM on the same day in the office Chamber of the Registrar General. ( Number of copies - 300 Nos ) REGISTRAR GENERAL {"h. Memo. No .HCM .II I46I20 1 6/Prc l l~t..t, A- Dt. Shg,the _l!_March.,2016 Copy to: 1. The Directorate of Information and Public Relation, Government of Meghalaya, Shillon g with a request for publication at the Government ~oved rate on 2 (two) local newspapers (one Engli::;h / Unc Klw~i) ~Th~ Systems Analyst for uploading in the Official Website. 3. Accounts Section 4. Office Notice Board. 5. Office File. ~~ REGISTRAR GENERAL ) TABLE OF CONTENTS SL.NO CONTENTS PAGE NO. 1 .. HISTORY 1-3 2 HIGH COURT HOLIDAY LIST 4 2016 3 HON'BLE THE CHIEF JUSTICE 5 AND JUDGES 4 RETIRED CHIEF JUSTICES 5 AND JUDGES 5 HON'BLE CHIEF JUSTICE 5 . WHO HAS BEEN ELEVATED TO SUPREME COURT 6 OFFICERS OF THE REGISTRY 6 HIGH COURT OF MEGHALAYA 7 MEGHALAYASTATELEGAL 7 SERVICES AUTHORITY/ ADVOCATE GENERAL 8 GOVERNOR'S SECRETARIAT 8 9 GOVERNMENT OF 9-14 MEGHALAYA 10 JUDICIAL OFFICERS IN THE 15-16 STATE OF MEGHALAYA . -

Newsletter E-Committee, Supreme Court of India
March, 2021 Newsletter e-Committee, Supreme Court of India Table of Contents Standard Operating Procedure (SOP) For Digital Preservation ................................................ 3 eCommittee Trains 4006 Advocate Master Trainers ................................................................ 4 Accessible Legal Eco System-Coordination Meeting with the CPCs of High Court. .................... 6 The First Virtual Court Of Chhattisgarh Inaugurated ............................................................... 7 High Court Of Meghalaya Launches Mobile Application. ......................................................... 8 ICJS Related E-Prosecution Software Training held By Meghalaya High Court ....................... 9 Justice Clocks Made Functional At Jodhpur & Jaipur Bench of Rajasthan High Court . ...........10 The Launch Of Mobile Application And Pagination Programme At HC Of Madhya Pradesh . ..11 Telangana State Judicial Academy Launches Official Website www.tsja.gov.in .....................13 NStep Training Programme At High Court of Madras .............................................................14 Coordination Meeting For Effective Implementation of E-Courts Project At HC Of Kerala. ......15 Know the Best Practices Of High Court Of Delhi & High Court of Gauhati ...............................16 High Court Of Himachal Pradesh Adds New Functionality In Display Board Software. ............17 Advocate Master Trainer Programme-Coordination meeting with State Judicial Academies. 18 e-Courts Awareness Programme Through National -

Government of India Ministry of Law & Justice Department
GOVERNMENT OF INDIA MINISTRY OF LAW & JUSTICE DEPARTMENT OF JUSTICE LOK SABHA UNSTARRED QUESTION NO. †2491 TO BE ANSWERED ON WEDNESDAY, THE 26th DECEMBER, 2018. Number of Courts in the Country †2491. SHRI KAPIL MORESHWAR PATIL: Will the Minister of LAW AND JUSTICE be pleased to state: (a) whether the Government is committed to double the number of courts in the country; (b) if so, the number of new courts set up in the country during the last three years, State-wise; (c) the time by which the Government proposes to fill up the vacant posts of new judicial officials / judges in the newly set up courts; and (d) the number of such courts proposed to be set up in Maharashtra? ANSWER MINISTER OF STATE FOR LAW AND JUSTICE AND CORPORATE AFFAIRS (SHRI P. P. CHAUDHARY) (a) & (b) : The new courts at District and below District / Subordinate (Tehsil / Taluka) level are established by the respective State Governments in consultation with the concerned High Courts. As per information made available by High Courts and State Governments, sanctioned strength of Judicial Officers of District / Subordinate Courts has increased from 20,214 in the year 2014 to 22,644 in the year, 2018. The State-wise details of sanctioned strength of Judicial Officers of District / Subordinate Courts in the years 2014 and 2018 are given in a Statement at Annexure-I. Judges of Supreme Court of India are appointed under Article 124 (2) of the Constitution of India and the Judges of High Courts are appointed under Articles 217 (1) and 224 of the Constitution of India. -

Atman September.Pmd
(A Biannual News Bulletin of the Gauhati High Court) Published from Guwahati for private circulation (The High Court of Assam, Nagaland, Mizoram and Arunachal Pradesh) Guwahati ::: Sixth Year ::: 11 th Issue :::September, 2014 Events organized during From the Chief Justice (Acting) April, 2014 to September, 2014 Keeping in view the changing trends of technology the Gauhati Foundation stone laying ceremony of CJM Court at Kokrajhar. High Court is not lagging behind. Training of Court Managers held on 30th April, 2014. The activities of the Legal Ser- vices Authority and the Judicial Weeklong training by Justice U.L. Bhat, Former Chief Academy, and events of the High Justice of Gauhati High Court to New Recruits and Court that take place, require to Senior Judicial Officers. be informed to all institutions and persons related Valedictory function of the Grade -III Judicial Officers with law as an information-sharing effort. The of Assam, Nagaland and Arunachal Pradesh. ATMAN in this direction is doing a wonderful job of showcasing the events conducted by the Legal Training of Para Legal Volunteers at Arunachal Pradesh. Services Authority and the Judicial Academy, and The Awareness Referral Coaching and Mentoring (ARCM) also the events that take place in the High Court. Programme on 24-05-2014 at Guwahati. I wish that ATMAN gets deserved readership un- Judicial discourse for the Judicial Officers of Kamrup (M), der affectionate patronage. Kamrup, Darrang, Mangaldai, Udalguri, Nalbari and Justice K. Sreedhar Rao Morigaon Districts on 14th and 15th June, 2014. Full Court Farewell Reference of Justice B.D.Agarwal. Editor speaks Full Court Farewell Reference of Justice B.P. -

Nber Working Paper Series Misallocation in the Market
NBER WORKING PAPER SERIES MISALLOCATION IN THE MARKET FOR INPUTS: ENFORCEMENT AND THE ORGANIZATION OF PRODUCTION Johannes Boehm Ezra Oberfield Working Paper 24937 http://www.nber.org/papers/w24937 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts Avenue Cambridge, MA 02138 August 2018 We are grateful to David Baqaee, Hugo Hopenhayn, Sam Kortum, Eduardo Morales, Steve Redding, Matt Rognlie, Meredith Startz, Felix Tintelnot, Gustavo Ventura, Chris Woodruff, and various seminar participants for helpful suggestions. Anusha Guha, Helene Maghin, and Juan Manuel Castro provided excellent research assistance. We are grateful to Daksh India for sharing data, and to CEPR/PEDL and the Sciences Po/Princeton partnership for financial support. Boehm thanks the International Economics Section at Princeton for hospitality during the later stages of the project. This document is an output from the research initiative “Private Enterprise Development in Low-Income Countries” (PEDL), a programme funded jointly by the by the Centre for Economic Policy Research (CEPR) and the Department for International Development (DFID), contract reference PEDL_LOA_4006_Boehm. The views expressed are not necessarily those of CEPR or DFID. All mistakes are our own. The views expressed herein are those of the authors and do not necessarily reflect the views of the National Bureau of Economic Research. NBER working papers are circulated for discussion and comment purposes. They have not been peer-reviewed or been subject to the review by the NBER Board of Directors that accompanies official NBER publications. © 2018 by Johannes Boehm and Ezra Oberfield. All rights reserved. Short sections of text, not to exceed two paragraphs, may be quoted without explicit permission provided that full credit, including © notice, is given to the source. -

HIGH COURT of MEGHALAYA at SHILLONG Cont.Cas(C)
Bar & Bench (www.barandbench.com) 1 Serial No. 1 Supplementary List HIGH COURT OF MEGHALAYA AT SHILLONG Cont.Cas(C) No. 37 of 2018 Arising out of WP(C) No. 337 of 2018 Date of Hearing : 25.02.2019 & 01.03.2019 Date of Decision: 08.03.2019 The Registrar General, Vs. Smti. Patricia Mukhim & Anr. High Court of Meghalaya. Coram: Hon’ble Mr. Justice Mohammad Yaqoob Mir, Chief Justice Hon’ble Mr. Justice S.R. Sen, Judge Appearance: For the Petitioner(s)/Appellant(s) : Mr. S. Dey, Amicus Curiae. Mr. N. Syngkon, Amicus Curiae. Mr. K. Ch. Gautam, Amicus Curiae. Mr. C.H. Mawlong, Amicus Curiae. For the Respondent(s) : Mr. K. Paul, Adv. with Mr. S. Thapa, Adv. i) Whether approved for reporting in Yes/No Law journals etc.: ii) Whether approved for publication in press: Yes/No S.R. Sen, ‘J’ 1. This contempt proceeding had to be initiated on the basis of the reports published in the “Shillong Times” dated 06.12.2018 and 10.12.2018 under the caption “When Judges judge for themselves”. The contents of the news item are reproduced herein below for ready reference and perusal: „High Court pursues retirement benefits to judges, family By Our Reporter SHILLONG: The High Court of Meghalaya has said the government should include spouse and children of retired judges for medical treatment and other facilities. Bar & Bench (www.barandbench.com) 2 During the hearing of the petition of Registrar General, the High Court of Meghalaya against the State Government on Wednesday, the single bench headed by Justice SR Sen said the additional advocate general filed an affidavit regarding medical facilities to retired judges. -

The High Court of Meghalaya Shillong
.. THE HIGH COURT OF MEGHALAYA SHILLONG . ============NOTIFICATION ~. Shillong, the~th ~. ~ No. HCM.II/120/2013/1155 - In pursuance to this Registry~s Notification No. HCM.II/333/2013/1171 - 72 A Dated 24th April, 2015 Mrs. B. Giri, MJS, has assumed charge of the Office of Registrar General, High Court of Meghalaya at Shillong w.e.f. 24th April, 2015. All the Correspondences, Confidential Matters, Demi-official Letters, Office Memorandum, Notifications, etc., requiring her attention may be addressed as under: "Mrs. B. Giri, MJS, Registrar General, High Court ofMeghalaya at Shillong, PIN-793001 Telephone No. 0364 - 2226675 Fax No. 0364 - 2500064" B~ ~.~) REGISTRAR Memo No. HCM.II/120/2013/1155 A Dated, Shillong 29th April, 2015. Copyto: 1. The ChiefSecretary to Government ofMeghalaya, Shillong. 2. The Advocate General, Meghalaya Shillong. 3. The Secretary General, Supreme Court ofIndia, New Delhi. 4. The Registrar General, Gauhati High Court, Guwahati. 5· The Registrar General, High Court ofKarnataka, Bangalore. 6. The Registrar General, Madras High Court, Chennai. 7- The Registrar General, High Court ofDelhi, New Delhi. 8. The Registrar General, Bombay High Court, Mumbai. 9. The Registrar General, High Court ofBihar, Patna. 10. The Registrar General, High Court ofMadhya Pradesh, Jabalpur. 11. The Registrar General, High Court ofWest Bengal, Calcutta, Kolkota. 12. The Registrar General, High Court ofUttar Pradesh, Allahabad. 13. The Registra-r General, Kerela High Court, Kochi. 14. The Registrw· General, High Court ofOrissa, Cuttack. 15. The Registrar General, High Court ofRajasthan, Jodhpur. 16. The Registrar General, High Court ofGujarat, at Sola (Ahmadabad). • Contd......2j ---2- 17. The Registrar General, High Court ofJammu & Kashmir at Srinagar. -

Dated 10Th January, 2019 Reg. Elevation
1 SUPREME COURT OF INDIA Re: Filling up vacancies of Judges in the Supreme Court. Against the sanctioned strength of 31 Judges, the Supreme Court of India is presently functioning with 26 Judges, leaving 05 clear vacancies. The Collegium comprising the Chief Justice of India and four senior-most Judges of the Supreme Court viz. Mr. Justices Madan B. Lokur, A.K. Sikri, S.A. Bobde and N.V. Ramana met on Wednesday, 12th December, 2018 to discuss the Agenda viz., (1) to consider and recommend names for appointment as Judges in the Supreme Court and (2) to consider proposals for transfer of Chief Justices and Judges of High Courts. The then Collegium on 12th December, 2018 took certain decisions. However, the required consultation could not be undertaken and completed as the winter vacation of the Court intervened. By the time the Court re-opened, the composition of the Collegium underwent a change. After extensive deliberations on 5th / 6th January, 2019, the newly constituted Collegium deemed it appropriate to have a fresh look at the matter and also to consider the proposals in the light of the additional material that became available. In terms of the above, this Collegium unanimously resolves to fill up, for the present, two of the five existing vacancies of Judges in the Supreme Court. The Collegium has discussed names of Chief Justices as well as senior puisne Judges of all High Courts, eligible for elevation to the Supreme Court. The Collegium is of the considered view that at present the following persons are more deserving and suitable in all respects than other Chief Justices and senior puisne Judges of High Courts, for being appointed as Judges of the Supreme Court of India: 2 1. -
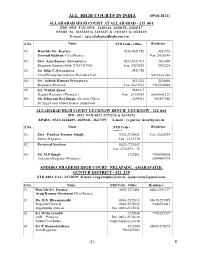
All High Courts in India (09.04.2021)
ALL HIGH COURTS IN INDIA (09.04.2021) ALLAHABAD HIGH COURT AT ALLAHABAD - 211 001 STD: 0532 FAX: 0532- 2420344, 2420152, 2420317 EPABX No. 2422335 to 2422337 & 2421611 to 2421618 E-mail : [email protected] S.No. Name STD Code - Office Residence 01. Hon'ble Mr. Justice 0532-2421742 2421730 Govind Mathur, Chief Justice Fax: 2420344 02. Shri Ajay Kumar Srivastava 0532-2421761 2421800 Registrar General (Mob: 8765711900) Fax: 2420152 2422214 03. Sri Dilip C.Srivastava 2421742 Chief Private Secretary to Hon’ble Chief 9415631036 04. JuSristii c eAshish Kumar Srivastava 2421222 2434646 Registrar (Protocol) Fax :2623511 9415218422 05. Sri Wahid Absar, 2420317 Deputy Registar ( Protocol ) Fax : 2420905 8004905529 06. Mr. Dharam Raj Singh, Section Officer 2644511 983837588 I/C High Court Guest House, Allahabad ALLAHABAD HIGH COURT LUCKNOW BENCH, LUCKNOW - 226 061 STD: 0522 FAX-0522-2272328 & 2624373 EPABX: 0522-2624489, 2628341, 2627395 E-mail : registrar [email protected] S.No. Name STD Code - Residence Office 01. Shri Pankaj Kumar Singh 0522-2722681 Fax: 2622414 Senior Registrar Fax : 2272570 02. Protocol Section 0522-2722553 Fax: 2722574 - 75 03. Sri M.P.Singh 2722501 9450906696 Assistant Registar (Protocol) 8004905719 ANDHRA PRADESH HIGH COURT NELAPADU, AMARAVATHI, GUNTUR DISTRICT - 522 239 STD:0863 FAX: 2372639, E-mail: [email protected], [email protected] S.No. Name STD Code - Office Residence 01. Hon’ble Sri Justice 0863-2372501 0866-2951277 Arup Kumar Goswami Chief Justice 02. Ms. B.S. Bhanumathi 0863-2372613 08645-295999 Registrar General 0863-2372622 9440621441 [email protected] Fax: 0863-2372631 03. Sri M.Gurunath 2372630 7901625207 OSD – Protocol Fax: 0863-2372639 Senior Civil Judge [email protected] 04.