DOCSLIB.ORG

Metrics a Metric Is a Way of Measuring the Distance Between Objects in a Set

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Metrics a Metric Is a Way of Measuring the Distance Between Objects in a Set Metrics A metric is a way of measuring the distance between objects in a set. Given a set S, a metric on S is a function d from S S to R such that for all x; y; z S, × 2 (i) d(x; x) = 0; (ii) d(x; y) > 0; x = y; 6 (iii) d(x; y) = d(y; x); (iv) d(x; z) d(x; y) + d(y; z) ≤ For most metrics, the first three properties are usually obviously satisfied. The fourth property, known as the Triangle Inequality, commonly requires a bit more effort to verify. Examples: The following functions are metrics on the stated sets: 1. S = R; d(x; y) = x y : j − j (i) d(x; x) = x x = 0 = 0 j − j j j (ii) x y 0; and x y = 0 if and only if x y = 0; that is x = y. j − j ≥ j − j − (iii) d(y; x) = y x = x y = d(x; y). j − j j − j (iv) For any real number, x x . ≤ j j Therefore x + y 2 = (x + y)2 j j = x2 + 2xy + y2 x 2 + 2 x y + y 2 ≤ j j j jj j j j =( x + y )2 j j j j Since x + y 0, we have j j j j ≥ x + y x + y j j ≤ j j j j and hence x z = (x y) + (y z) x y + y z : j − j j − − j ≤ j − j j − j 1 2 2. S = Rn; n 1=2 2 d(x; y) = (x1 yi) ! X − i=1 1=2 = (x y):(x y) − − = x y jj − jj This is usually referred to as the Euclidean metric. To prove (iv), consider (x + ty):(x + ty) = x 2 + 2t(x:y) + t2 y 2 jj jj jj jj where t is a real variable. Since this quadratic expression in t is always 0, the discriminant ≥ 4 x 2 y 2 4(x:y)2 jj jj jj jj − is non-negative. Therefore x:y x y ≤ jj jj jj jj x + y 2 = x 2 + 2x:y + y 2 jj jj jj jj jj jj 2 x 2 + 2 x y + y 2 = x + y ≤ jj jj jj jj jj jj jj jj jj jj jj jj x + y x + y jj jj ≤ jj jj jj jj and d(x; z) = x z jj − jj = x y + y z jj − − jj x y + y z ≤ jj − jj jj − jj d(x; y) + d(y; z) ≤ 3. S = C; d(z1; z2) = z1 z2 : j − j Since 2 2 1=2 z1 z2 = (x1 x2) + (y1 y2) j − j − − this is covered by the previous example. 4. S = Rn; n d(x; y) = xi yi X j − j i=1 This is sometimes known as the taxi cab metric. 3 Since xi zi = xi yi + yi zi xi yi + yi zi j − j j − − j ≤ j − j j − j d(x; z) d(x; y) + d(y; z) : ≤ 5. S = Rn; d(x; y) = max xi yi i j − j This is known as the sup metric. d(x; z) = xj zj for some j j − j xj yj + yj zj ≤ j − j j − j d(x; y) + d(y; z) ≤ 6. S arbitrary; d(x; y) = 1; x = y 6 d(x; x) = 0 : (This is known as the discrete metric.) To prove the triangle inequality, we note that if z = x, d(x; z) = 0 d(x; y) + d(y; z) ≤ for any choice of y, while if z = x then either z = y or x = y (at least) so that 6 6 6 d(x; y) + d(y; z) 1 = d(x; z) ≥ 7. S is the set of all real continuous functions on [a; b]. 1 b 2 2 d(f; g) = Z (f(x) g(x)) dx! : a − This is the continuous equivalent of the Euclidean metric in Rn. The proof of the triangle inequality follows the same form as in that case. 8. S as in 7. d(f; g) = max f(x) g(x) : a x b j − j ≤ ≤ This is the continuous equivalent of the sup metric. The proof of the triangle inequality is virtually identical. 4 9. S arbitrary; d(x; y) = D(x; y)=(1 + D(x; y)), where D(x; y) is another metric on S. d(x; y) + d(y; z) d(x; z) − D(x; y)(1 + D(y; z) + D(x; z) + D(y; z)D(x; z)) = (1 + D(x; y))(1 + D(y; z))(1 + D(x; z)) D(y; z)(1 + D(x; y) + D(x; z) + D(x; y)D(x; z)) + (1 + D(x; y))(1 + D(y; z))(1 + D(x; z)) D(x; z)(1 + D(y; z) + D(x; y) + D(y; z)D(x; y)) − (1 + D(x; y))(1 + D(y; z))(1 + D(x; z)) D(x; y) + D(y; z) D(x; z) = − (1 + D(x; y))(1 + D(y; z))(1 + D(x; z)) 2D(x; y)D(y; z) + D(x; y)D(y; z)D(x; z) + (1 + D(x; y))(1 + D(y; z))(1 + D(x; z)) 0 ≥ since the denominator is positive, and the numerator is non-negative. 10. Let f be a twice differentiable real function defined for x 0, and such that ≥ f(0) = 0(a) f 0(x) > 0 x 0(b) ≥ f 00(x) 0 x 0(c) ≤ ≥ Then if d(x; y) is a metric on the set S, so is f(d(x; y)). Since f 0(x) > 0, we have from the Mean Value Theorem f(x) f(y) = f 0(θ)(x y) − − f(x) > f(y) ; x > y : In particular, since f(0) = 0, f(x) > 0 ; x > 0 : If a 0 and s 0, then by the Mean Value Theorem we also have ≥ ≥ f 0(a + s) f 0(s) = f 00(θ)s 0 − ≤ f 0(a + s) f 0(s) ≤ and if b 0 also ≥ b b Z f 0(a + s) ds Z f 0(s) ds 0 ≤ 0 f(a + b) f(a) f(b) f(0) = f(b) − ≤ − f(a + b) f(a) + f(b) ≤ Since d(x; z) d(x; y) + d(y; z), ≤ f(d(x; z)) f(d(x; y) + d(y; z)) ≤ f(d(x; y)) + f(d(y; z) ≤ 5 Three important inequalities Definitions: If p and q are both > 1, we say that they are dual indices if 1 1 + = 1 : p q For x Rn, we define 2 n 1=p p x p = xi ! jj jj X j j i=1 Young's inequality. For x and y positive real numbers, and dual indices p and q, 1 1 xy xp + yq : ≤ p q Proof Fix y > 0, and consider the function 1 f(x) = xy xp − p for x > 0. p 1 p 2 f 0(x) = y x − ; f 00(x) = (p 1)x − < 0 − − − p 1 1=(p 1) Therefore f has a global maximum when y = x − , x = y − , and 1 p 1+1=(p 1) 1 p=(p 1) 1 q xy x y − y − = y − p ≤ − p q H¨older'sinequality For x and y in Rn, n xiyi x p y q X j j ≤ jj jj jj jj i=1 where p and q are dual indices. Proof If either x = 0 or y = 0 the result is trivially true. Otherwise, for each i xi yi j j 0; j j 0 x p ≥ y q ≥ jj jj jj jj and therefore by Young's inequality p q xi yi 1 xi 1 yi j jj j j j p + j j q x p y q ≤ p x p q y q jj jj jj jj jj jj jj jj Summing from i = 1 to n, we have 1 n 1 1 xiyi + = 1 : x p y q X j j ≤ p q jj jj jj jj i=1 6 Minkowski's inequality For x and y in Rn, and p > 1, x + y p x p + y p : jj jj ≤ jj jj jj jj n p p 1 x + y = xi + yi xi + yi − jj jjp X j j j j i=1 n n p 1 p 1 xi xi + yi − + yi xi + yi − ≤ X j jj j X j jj j i=1 i=1 j n 1=q (p 1)q x p xi + yi − ! ≤ jj jj X j j i 1 − n 1=q (p 1)q + y p xi + yi − ! jj jj X j j i 1 − p=q n 1=p 2 p 3 = x p + y p xi + yi ! jj jj jj jj X j j 4 i=1 5 p 1 = x p + y p x + y − jj jj jj jj jj jjp Minkowski's inequality shows that d(x; y) = x y p jj − jj is a metric on Rn. If we consider the limits p 1 and p , we obtain the taxicab and sup metrics which we have already! seen. ! 1 The Euclidean metric corresponds to p = 2. These metrics can be extended to infinite real sequences xi 1 : f gi=1 p If l is the set of all sequences xi for which f g 1 p xi ; p 1 X j j ≥ i=1 converges, then the norm 1=p 1 p x p = xi ! jj jj X j j i=1 induces a metric on lp in the same way as the finite form does on Rn.
Load more

Recommended publications
  • Inner Product Spaces Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 2, 2007)
    MAT067 University of California, Davis Winter 2007 Inner Product Spaces Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 2, 2007) The abstract definition of vector spaces only takes into account algebraic properties for the addition and scalar multiplication of vectors. For vectors in Rn, for example, we also have geometric intuition which involves the length of vectors or angles between vectors. In this section we discuss inner product spaces, which are vector spaces with an inner product defined on them, which allow us to introduce the notion of length (or norm) of vectors and concepts such as orthogonality. 1 Inner product In this section V is a finite-dimensional, nonzero vector space over F. Definition 1. An inner product on V is a map ·, · : V × V → F (u, v) →u, v with the following properties: 1. Linearity in first slot: u + v, w = u, w + v, w for all u, v, w ∈ V and au, v = au, v; 2. Positivity: v, v≥0 for all v ∈ V ; 3. Positive definiteness: v, v =0ifandonlyifv =0; 4. Conjugate symmetry: u, v = v, u for all u, v ∈ V . Remark 1. Recall that every real number x ∈ R equals its complex conjugate. Hence for real vector spaces the condition about conjugate symmetry becomes symmetry. Definition 2. An inner product space is a vector space over F together with an inner product ·, ·. Copyright c 2007 by the authors. These lecture notes may be reproduced in their entirety for non- commercial purposes. 2NORMS 2 Example 1. V = Fn n u =(u1,...,un),v =(v1,...,vn) ∈ F Then n u, v = uivi.
    [Show full text]
  • 5-7 the Pythagorean Theorem 5-7 the Pythagorean Theorem
    55-7-7 TheThe Pythagorean Pythagorean Theorem Theorem Warm Up Lesson Presentation Lesson Quiz HoltHolt McDougal Geometry Geometry 5-7 The Pythagorean Theorem Warm Up Classify each triangle by its angle measures. 1. 2. acute right 3. Simplify 12 4. If a = 6, b = 7, and c = 12, find a2 + b2 2 and find c . Which value is greater? 2 85; 144; c Holt McDougal Geometry 5-7 The Pythagorean Theorem Objectives Use the Pythagorean Theorem and its converse to solve problems. Use Pythagorean inequalities to classify triangles. Holt McDougal Geometry 5-7 The Pythagorean Theorem Vocabulary Pythagorean triple Holt McDougal Geometry 5-7 The Pythagorean Theorem The Pythagorean Theorem is probably the most famous mathematical relationship. As you learned in Lesson 1-6, it states that in a right triangle, the sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse. a2 + b2 = c2 Holt McDougal Geometry 5-7 The Pythagorean Theorem Example 1A: Using the Pythagorean Theorem Find the value of x. Give your answer in simplest radical form. a2 + b2 = c2 Pythagorean Theorem 22 + 62 = x2 Substitute 2 for a, 6 for b, and x for c. 40 = x2 Simplify. Find the positive square root. Simplify the radical. Holt McDougal Geometry 5-7 The Pythagorean Theorem Example 1B: Using the Pythagorean Theorem Find the value of x. Give your answer in simplest radical form. a2 + b2 = c2 Pythagorean Theorem (x – 2)2 + 42 = x2 Substitute x – 2 for a, 4 for b, and x for c. x2 – 4x + 4 + 16 = x2 Multiply.
    [Show full text]
  • Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014
    Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014 The “Three Possibilities” Property: either a>b, a=b, or a<b The Transitive Property: If a>b and b>c, then a>c The Addition Property: If a>b, then a+c>b+c The Subtraction Property: If a>b, then a‐c>b‐c The Multiplication Property: If a>b and c>0, then ac>bc The Division Property: If a>b and c>0, then a/c>b/c The Addition Theorem of Inequality: If a>b and c>d, then a+c>b+d The “Whole Greater than Part” Theorem: If a>0, b>0, and a+b=c, then c>a and c>b Def: An exterior angle of a triangle is an angle that forms a linear pair with an angle of the triangle. A In ∆ABC, exterior ∠2 forms a linear pair with ∠ACB. The other two angles of the triangle, ∠1 (∠B) and ∠A are called remote interior angles with respect to ∠2. 1 2 B C Theorem 12: The Exterior Angle Theorem An Exterior angle of a triangle is greater than either remote interior angle. Find each of the following sums. 3 4 26. ∠1+∠2+∠3+∠4 2 1 6 7 5 8 27. ∠1+∠2+∠3+∠4+∠5+∠6+∠7+ 9 12 ∠8+∠9+∠10+∠11+∠12 11 10 28. ∠1+∠5+∠9 31. What does the result in exercise 30 indicate about the sum of the exterior 29. ∠3+∠7+∠11 angles of a triangle? 30. ∠2+∠4+∠6+∠8+∠10+∠12 1 Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014 After proving the Exterior Angle Theorem, Euclid proved that, in any triangle, the sum of any two angles is less than 180°.
    [Show full text]
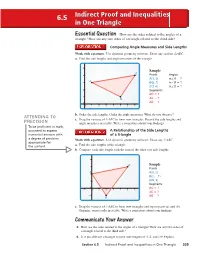
  • Indirect Proof and Inequalities in One Triangle
    6.5 Indirect Proof and Inequalities in One Triangle EEssentialssential QQuestionuestion How are the sides related to the angles of a triangle? How are any two sides of a triangle related to the third side? Comparing Angle Measures and Side Lengths Work with a partner. Use dynamic geometry software. Draw any scalene △ABC. a. Find the side lengths and angle measures of the triangle. 5 Sample C 4 Points Angles A(1, 3) m∠A = ? A 3 B(5, 1) m∠B = ? C(7, 4) m∠C = ? 2 Segments BC = ? 1 B AC = ? AB = 0 ? 01 2 34567 b. Order the side lengths. Order the angle measures. What do you observe? ATTENDING TO c. Drag the vertices of △ABC to form new triangles. Record the side lengths and PRECISION angle measures in a table. Write a conjecture about your fi ndings. To be profi cient in math, you need to express A Relationship of the Side Lengths numerical answers with of a Triangle a degree of precision Work with a partner. Use dynamic geometry software. Draw any △ABC. appropriate for the content. a. Find the side lengths of the triangle. b. Compare each side length with the sum of the other two side lengths. 4 C Sample 3 Points A A(0, 2) 2 B(2, −1) C 1 (5, 3) Segments 0 BC = ? −1 01 2 3456 AC = ? −1 AB = B ? c. Drag the vertices of △ABC to form new triangles and repeat parts (a) and (b). Organize your results in a table. Write a conjecture about your fi ndings.
    [Show full text]
  • CS261 - Optimization Paradigms Lecture Notes for 2013-2014 Academic Year
    CS261 - Optimization Paradigms Lecture Notes for 2013-2014 Academic Year ⃝c Serge Plotkin January 2014 1 Contents 1 Steiner Tree Approximation Algorithm 6 2 The Traveling Salesman Problem 10 2.1 General TSP . 10 2.1.1 Definitions . 10 2.1.2 Example of a TSP . 10 2.1.3 Computational Complexity of General TSP . 11 2.1.4 Approximation Methods of General TSP? . 11 2.2 TSP with triangle inequality . 12 2.2.1 Computational Complexity of TSP with Triangle Inequality . 12 2.2.2 Approximation Methods for TSP with Triangle Inequality . 13 3 Matchings, Edge Covers, Node Covers, and Independent Sets 22 3.1 Minumum Edge Cover and Maximum Matching . 22 3.2 Maximum Independent Set and Minimum Node Cover . 24 3.3 Minimum Node Cover Approximation . 24 4 Intro to Linear Programming 27 4.1 Overview . 27 4.2 Transformations . 27 4.3 Geometric interpretation of LP . 29 4.4 Existence of optimum at a vertex of the polytope . 30 4.5 Primal and Dual . 32 4.6 Geometric view of Linear Programming duality in two dimensions . 33 4.7 Historical comments . 35 5 Approximating Weighted Node Cover 37 5.1 Overview and definitions . 37 5.2 Min Weight Node Cover as an Integer Program . 37 5.3 Relaxing the Linear Program . 37 2 5.4 Primal/Dual Approach . 38 5.5 Summary . 40 6 Approximating Set Cover 41 6.1 Solving Minimum Set Cover . 41 7 Randomized Algorithms 46 7.1 Maximum Weight Crossing Edge Set . 46 7.2 The Wire Routing Problem . 48 7.2.1 Overview .
    [Show full text]
  • Use the Converse of the Pythagorean Theorem
    Use the Converse of the Pythagorean Theorem Goal • Use the Converse of the Pythagorean Theorem to determine if a triangle is a right triangle. Your Notes THEOREM 7.2: CONVERSE OF THE PYTHAGOREAN THEOREM If the square of the length of the longest side of a triangle is equal aI to the sum of the squares of the c A lengths of the other two sides, then the triangle is a triangle. If c2 = a 2 + b2, then AABC is a triangle. Verify right triangles Tell whether the given triangle is a right triangle. a. b. 24 6 9 Solution Let c represent the length of the longest side of the triangle. Check to see whether the side lengths satisfy the equation c 2 = a 2 + b 2. a. ( )2 ? 2 + 2 • The triangle a right triangle. b. 2? 2 + 2 The triangle a right triangle. 174 Lesson 7.2 • Geometry Notetaking Guide Copyright @ McDougal Littell/Houghton Mifflin Company. Your Notes THEOREM 7.3 A If the square of the length of the longest b c side of a triangle is less than the sum of B the squares of the lengths of the other C a two sides, then the triangle ABC is an triangle. If c 2 < a 2 + b2 , then the triangle ABC is THEOREM 7.4 A If the square of the length of the longest bN side of a triangle is greater than the sum of C B the squares of the lengths of the other two a sides, then the triangle ABC is an triangle.
    [Show full text]
  • Inequalities for C-S Seminorms and Lieb Functions
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Elsevier - Publisher Connector LINEAR ALGEBRA AND ITS APPLiCATIONS ELSEVIER Linear Algebra and its Applications 291 (1999) 103-113 - Inequalities for C-S seminorms and Lieb functions Roger A. Horn a,., Xingzhi Zhan b.l ;1 Department (?(Mathematics, Uni('('rsify of Utah, Salt L(lke CifY, UT 84103. USA h Institute of Mathematics. Pekins; University, Beijing 10087J. People's Republic of C/WICt Received 3 July 1998: accepted 3 November 1998 Submitted by R. Bhatia Abstract Let AI" be the space of 1/ x 11 complex matrices. A seminorm /I ." on NI" is said to be a C-S seminorm if IIA-AII = IIAA"II for all A E Mil and IIAII ~ IIBII whenever A, B, and B-A are positive semidefinite. If II . II is any nontrivial C-S seminorm on AI", we show that 111/'111 is a unitarily invariant norm on M,n which permits many known inequalities for unitarily invariant norms to be generalized to the setting of C-S seminorrns, We prove a new inequality for C-S seminorms that includes as special cases inequalities of Bhatia et al., for unitarily invariant norms. Finally. we observe that every C-S seminorm belongs to the larger class of Lieb functions, and we prove some new inequalities for this larger class. © 1999 Elsevier Science Inc. All rights reserved. 1. Introduction Let M" be the space of 11 x Jl complex matrices and denote the matrix ab­ solute value of any A E M" by IA I=(A* A)1/2.
    [Show full text]
  • Simplex-Tree Based Kinematics of Foldable Objects As Multi-Body Systems Involving Loops
    Simplex-Tree Based Kinematics of Foldable Objects as Multi-body Systems Involving Loops Li Han and Lee Rudolph Department of Mathematics and Computer Science Clark University, Worcester, MA 01610 Email: [email protected], [email protected] Abstract— Many practical multi-body systems involve loops. Smooth manifolds are characterized by the existence of local Studying the kinematics of such systems has been challenging, coordinates, but although some manifolds are equipped with partly because of the requirement of maintaining loop closure global coordinates (like the joint angle parameters, in the constraints, which have conventionally been formulated as highly nonlinear equations in joint parameters. Recently, novel para- cases of a serial chain without closure constraints or [7, 8] a meters defined by trees of triangles have been introduced for a planar loop satisfying the technical “3 long links” condition), broad class of linkage systems involving loops (e.g., spatial loops typically a manifold has neither global coordinates nor any with spherical joints and planar loops with revolute joints); these standard atlas of local coordinate charts. Thus, calculations parameters greatly simplify kinematics related computations that depend on coordinates are often difficult to perform. and endow system configuration spaces with highly tractable piecewise convex geometries. In this paper, we describe a more Some recent kinematic work uses new parameters that are general approach for multi-body systems, with loops, that allow not conventional joint parameters. One series of papers [9, construction trees of simplices. We illustrate the applicability and 10, 11, 12, 13] presented novel formulations and techniques, efficiency of our simplex-tree based approach to kinematics by a including distance geometry, linear programming and flag study of foldable objects.
    [Show full text]
  • Find X. 9. SOLUTION: in a Right Triangle, the Sum of the Squares Of
    8-2 The Pythagorean Theorem and Its Converse Find x. 9. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is x and the lengths of the legs are 12 and 16. 10. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is 15 and the lengths of the legs are 9 and x. eSolutions11. Manual - Powered by Cognero Page 1 SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is 5 and the lengths of the legs are 2 and x. 12. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is 66 and the lengths of the legs are 33 and x. 13. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is x and the lengths of the legs are . 14. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
    [Show full text]
  • Tet Trouble Solution
    AFRICAN INSTITUTE FOR MATHEMATICAL SCIENCES SCHOOLS ENRICHMENT CENTRE TEACHER NETWORK TET TROUBLE Show that is it impossible to have a tetrahedron whose six edges have lengths 10, 20, 30, 40, 50 and 60 units. Is it possible for a tetrahedron to have edges of lengths 10, 20, 25, 45, 50 and 60 units? Can you write general rules for someone else to use to check whether a given six lengths could form the edges of a tetrahedron? SOLUTION It is impossible to have a tetrahedron which has edge lengths of 10, 20, 30, 40, 50 and 60 units. This is because to produce a triangle two sides have to be bigger (when added together) than the third. This is called the TRIANGLE INEQUALITY. So this tetrahedron won't work because the 10 is too small to make a triangle. e.g. 10, 20, 30 • 20 + 30 > 10 (OK) • 10 + 30 > 20 (OK) • but 10 + 20 = 30 so the triangle becomes a straight line. 10 will not go with any other two numbers in the above list. It is possible to make a tetrahedron which has lengths 10, 20, 25, 45, 50 and 60 units. The reason is that the numbers are big and small enough to fit the triangle inequality (the sum of two sides bigger than the third). Here is a net of this tetrahedron to explain this answer (not to scale!) Triangle 1 10 + 25 > 20 Triangle 2 10 + 50 > 45 10 + 20 > 25 10 + 45 > 50 20 + 25 > 10 50 + 45 > 10 Triangle 3 50 + 60 > 25 Triangle 4 60 + 45 > 20 25 + 60 > 50 20 + 60 > 45 25 + 50 > 60 20 + 45 > 60 All four faces satisfy the triangle inequality, so it can make a tetrahedron.
    [Show full text]
  • Normed Vector Spaces
    Chapter II Elements of Functional Analysis Functional Analysis is generally understood a “linear algebra for infinite di- mensional vector spaces.” Most of the vector spaces that are used are spaces of (various types of) functions, therfeore the name “functional.” This chapter in- troduces the reader to some very basic results in Functional Analysis. The more motivated reader is suggested to continue with more in depth texts. 1. Normed vector spaces Definition. Let K be one of the fields R or C, and let X be a K-vector space. A norm on X is a map X 3 x 7−→ kxk ∈ [0, ∞) with the following properties (i) kx + yk ≤ kxk + kyk, ∀ x, y ∈ X; (ii) kλxk = |λ| · kxk, ∀ x ∈ X, λ ∈ K; (iii) kxk = 0 =⇒ x = 0. (Note that conditions (i) and (ii) state that k . k is a seminorm.) Examples 1.1. Let K be either R or C, and let J be some non-empty set. A. Define `∞(J) = α : J → : sup |α(j)| < ∞ . K K j∈J We equip the space `∞(J) with the -vector space structure defined by point-wise K K addition and point-wise scalar multiplication. This vector space carries a natural norm k . k∞, defined by kαk = sup |α(j)|, α ∈ `∞(I). ∞ K j∈J When = , the space `∞(J) is simply denoted by `∞(J). When J = - the set K C C N of natural numbers - instead of `∞( ) we simply write `∞, and instead of `∞( ) R N R N we simply write `∞. B. Consider the space K c0 (J) = α : J → K : inf sup |α(j)| = 0 .
    [Show full text]
  • 6.7 Cauchy-Schwarz Inequality
    6.7 Cauchy-Schwarz Inequality Recall that we may write a vector u as a scalar multiple of a nonzero vector v, plus a vector orthogonal to v: hu; vi hu; vi u = v + u − v : (1) kvk2 kvk2 The equation (1) will be used in the proof of the next theorem, which gives one of the most important inequalities in mathematics. Theorem 16 (Cauchy-Schwarz Inequality). If u; v 2 V , then jhu; vij ≤ kukkvk: (2) This inequality is an equality if and only if one of u; v is a scalar multiple of the other. Proof. Let u; v 2 V . If v = 0, then both sides of (2) equal 0 and the desired inequality holds. Thus we can assume that v 6= 0. Consider the orthogonal decomposition hu; vi u = v + w; kvk2 where w is orthogonal to v (here w equals the second term on the right side of (1)). By the Pythagorean theorem, 2 2 hu; vi 2 kuk = v + kwk kvk2 jhu; vij2 = + kwk2 kvk2 jhu; vij2 ≥ : kvk2 Multiplying both sides of this inequality by kvk2 and then taking square roots gives the Cauchy-Schwarz inequality (2). Looking at the proof of the Cauchy-Schwarz inequality, note that (2) is an equality if and only if the last inequality above is an equality. Obviously this happens if and only if w = 0. But w = 0 if and only if u is a multiple of v. Thus the Cauchy-Schwarz inequality is an equality if and only if u is a scalar multiple of v or v is a scalar multiple of u (or both; the phrasing has been chosen to cover cases in which either u or v equals 0).
    [Show full text]