DOCSLIB.ORG

Math 321: Introduction to Mathematical Software

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Math 321: Introduction to Mathematical Software Math 321: Introduction to Mathematical Software David Koslicki, PhD 001 Part 1: Matlab page 008 Part 2: Mathematica page 058 Part 3: LATEX page 157 Part 4: Projects page 189 002 MTH 321: Introduction to Mathematical Software Catalog Description: An examination of select mathematical software packages to support problem solving. Topics include using computational resources to solve basic numerical and symbolic problems in mathematics, visualization and presen- tation of data, creation of simple programming scripts, and applications of basic programming techniques to promote mathematical understanding. The scientific typesetting language LaTeX will also be covered. All courses used to satisfy MTH prerequisites must be completed with a C- or better. Credits: 3 Meets: Two 80 minute classes meeting weekly for 10 weeks in a computer labo- ratory. Terms offered: F,S Enforced Prerequisites: MTH 252 and either MTH 341 or 306. Course Content: This course is designed to familiarize students with the use of software resources commonly utilized in the mathematical sciences. Students will learn how to use modern computing environments such as MATLAB and Mathematica for the purpose of symbolic and numerical problem solving and vi- sualization. Students will become acquainted with the syntax and usage of each system through computer-aided lectures as well as through projects. The relative merits and disadvantages of each system will also be discussed. Basic program- ming paradigms and concepts will be introduced where appropriate. This course will also introduce LaTeX, the de facto standard for the communication and pub- lication of mathematical and scientific documents. Learning Resources: In lieu of a text, relevant information will be posted on blackboard: http://www.my.oregonstate.edu. (All materials will be updated to canvas when appropriate.) Learning Outcomes for MTH 482: A successful student in MTH 399 will be able to use MATLAB and Mathematica to: 1. Solve basic numerical and symbolic mathematics problems. 2. Visualize and present data. 3. Create simple programming scripts and functions. 4. Understand and apply basic programming techniques and paradigms In addition, a successful student will be able to typeset and communicate mathe- matical results using LaTeX. Evaluation of Student Learning: The grading of the course is on a points-based system: Homework: 300 points Project: 100 points Total: 400 points 1 003 Students with Disabilities: Accommodations are collaborative efforts between students, faculty and Disability Access Services (DAS). Students with accommo- dations approved through DAS are responsible for contacting the faculty member in charge of the course prior to or during the first week of the term to discuss accommodations. Students who believe they are eligible for accommodations but who have not yet obtained approval through DAS should contact DAS immediately at 541-737-4098. Consult http://ds.oregonstate.edu/home. Student Conduct: All students are expected to obey OSU's student conduct regulations. In particular, students are expected to be honest and ethical in their academic work. Academic dishonesty is defined as an intentional act of deception in one of the following areas: Cheating - use or attempted use of unauthorized materials, information or study aids; Fabrication - falsification or invention of any information; Assisting - helping another commit an act of academic dishonesty; Tampering - altering or interfering with evaluation instruments and documents; Plagiarism - representing the words or ideas of another person as one's own. If evidence of academic dishonesty is found, University procedures will be followed, including the assignment of a grade of "F" for the guilty parties. For more infor- mation about academic integrity and the University's policies and procedures in this area, visit the Student Conduct web site at http://studentlife.oregonstate.edu/studentconduct/offenses-0 2 004 Syllabus Introduction to Mathematical Software Math 399, 3 credits Fall Quarter, 2014 Prerequisite: MTH 252 and MTH 341 or 306. Course Content: This course is designed to familiarize students with the use of software resources commonly utilized in the mathematical sciences. Students will learn how to use modern computing environments such as MATLAB and Mathematica for the purpose of symbolic and numerical problem solving and visualization. Students will become acquainted with the syntax and usage of each system through computer-aided lectures as well as through projects. The relative merits and disadvantages of each system will also be discussed. Basic programming paradigms and concepts will be introduced where appropriate. This course will also introduce LaTeX, the de facto standard for the communication and publication of mathematical and scientific documents. Learning Outcomes: A successful student in MTH 399 will be able to use MATLAB and Mathematica to: 1. Solve basic numerical and symbolic mathematics problems. 2. Visualize and present data. 3. Create simple programming scripts and functions. 4. Understand and apply basic programming techniques and paradigms In addition, a successful student will be able to typeset and communicate mathematical results using LaTeX. Meeting times: Tuesday and Thursday, 10:00am-11:20am, KIDD 033. Text: In lieu of a text, relevant information will be posted on blackboard: http://www.my.oregonstate.edu Professor: Dr. David Koslicki (“cause-lick-ee”) Office: KIDD 354 Phone: 514-737-5172 Email: [email protected] Office Hours: By appointment and T, R: 8-9am No appointments are required during office hours. 005 Homework: Homework assignments (along with their due dates) are contained in the course notes posted on blackboard. The due date for each homework assignment will typically be 3-7 days after it is assigned. Please attend class and keep an eye on the blackboard website for the homework assignment due dates. There will be at least 10 homework assignments, with the lowest two scores being dropped. Exams/Projects: In lieu of exams/quizzes, you will complete a final project. This project will consist of taking a math, science, or data related problem and writing a Matlab or Mathematica program to solve it. You will then summarize your results (including figures) in a LaTeX document and submit this (along with the source code) during finals week. Briefly, you will be graded on correctness and completeness of the source code (including how well commented the code is), along with how well written and presented the LaTeX document is. There are a couple of example projects posted on blackboard. You may either choose to perform one of these projects, or come up with your own. Please make an appointment with me (before dead week) to discuss what you project will consist of. Some other project ideas include: personal analytics (via location-based apps, email frequency analysis, personal genomics, etc.), constructing an interactive Fractal plotting program, investigating cellular automata, bioinformatics applications (eg. visualization of de Bruijn graphs). I am more than happy to look at your code/LaTeX document and give feedback about your project (but I will not be making any meetings during finals week, so start working on this early!). A 369-400 points A- 360-368 points Grading Policy: B+ 342-359 points The grading of the course is on a points-based system: B 323-341 points Homework: 300 points B- 320-328 points Project: 100 points C+ 311-319 points Total: 400 points C 280-310 points D 240-279 points F 000-239 points I reserve the right to alter this grading scheme at the end of the term, but only to your advantage. Help: Make a note of my office hours. I will be glad to help you whenever I can - just ask! 006 Your classmates are an important resource. There are many locations on campus for study groups to meet and work. The Mathematics Learning Center is an excellent place to study and meet with your classmates. Be sure you are working together towards understanding the solution, not just "getting the answer". Tutoring (free of charge) is available in the Mathematics Learning Center (Kidd 108) and in the Library. Disability Access Services: Accommodations are collaborative efforts between students, faculty and Disability Access Services (DAS). Students with accommodations approved through DAS are responsible for contacting the faculty member in charge of the course prior to or during the first week of the term to discuss accommodations. Students who believe they are eligible for accommodations but who have not yet obtained approval through DAS should contact DAS immediately at 541-737-4098. More information is available at http://ds.oregonstate.edu. Academic Dishonesty: Students are expected to be honest and ethical in their academic work. Academic dishonesty is defined as an intentional act of deception in one of the following areas: Cheating - use or attempted use of unauthorized materials, information or study aids; Fabrication - falsification or invention of any information; Assisting - helping another commit an act of academic dishonesty; Tampering - altering or interfering with evaluation instruments and documents; Plagiarism - representing the words or ideas of another person as one's own. If evidence of academic dishonesty is found, University procedures will be followed, including the assignment of a grade of “F” for the guilty parties. For more information about academic integrity and the University's policies and procedures in this area, visit the Student Conduct web
Load more

Recommended publications
  • Developing Scientific Computing Software: Current Processes And
    DEVELOPING: SGIENffl&Pifli|ii^Mp| CURRENT PROCESSES" WMWiiiiia DEVELOPING SCIENTIFIC COMPUTING SOFTWARE MASTER OF APPLIED SCIENCE(2008) McMaster University COMPUTING AND SOFTWARE Hamilton, Ontario TITLE: Developing Scientific Computing Software: Current Processes and Future Directions AUTHOR: Jin Tang, M.M. (Nanjing University) SUPERVISOR: Dr. Spencer Smith NUMBER OF PAGERS: xxii, 216 n Abstract Considerable emphasis in scientific computing (SC) software development has been placed on the software qualities of performance and correctness. How ever, other software qualities have received less attention, such as the qualities of usability, maintainability, testability and reusability. Presented in this work is a survey titled "Survey on Developing Scien tific Computing Software, which is apparently the first conducted to explore the current approaches to SC software development and to determine which qualities of SC software are in most need of improvement. From the survey. we found that systematic development process is frequently not adopted in the SC software community, since 58% of respondents mentioned that their entire development process potentially consists only of coding and debugging. Moreover, semi-formal and formal specification is rarely used when developing SC software, which is suggested by the fact that 70% of respondents indicate that they only use informal specification. In terms of the problems in SC software development, which are dis covered by analyzing the survey results, a solution is proposed to improve the quality of SC software by using SE methodologies, concretely, using a modified Parnas' Rational Design Process (PRDP) and the Unified Software Development Process (USDP). A comparison of the two candidate processes is provided to help SC software practitioners determine which of the two pro cesses fits their particular situation.
    [Show full text]
  • The Guide to Available Mathematical Software Problem Classification System
    The Guide to Available Mathematical Software Problem Classification System Ronald F. Boisvert, Sally E. Howe and David K. Kahaner November 1990 U.S. DEPARTMENT OF COMMERCE National Institute of Standards and Technology Gaithersburg, MD 20899 100 U56 //4475 1990 C.2 NATIONAL, INSrrnJTE OF STANDARDS & TECHNOLOGY / THE GUIDE TO AVAILABLE MATHEMATICAL SOFTWARE PROBLEM CLASSIFICATION SYSTEM Ronald F. Boisvert Sally E. Howe David K. Kahaner U.S. DEPARTMENT OF COMMERCE National InstHute of Standards and Technology Center for Computing and Applied Mathematics Gaithersburg, MO 20899 November 1990 U.S. DEPARTMENT OF COMMERCE Robert A. Mosbacher, Secretary NATIONAL INSTITUTE OF STANDARDS AND TECHNOLOGY John W. Lyons, Director 2 Boisvert, Howe and Kahaner own manuals or on-line documentation system. In order to determine what software is avail- able to solve a particular problem, users must search through a very large, heterogeneous collection of information. This is a tedious and error-prone process. As a result, there has been much interest in the development of automated advisory systems to help users select software. Keyword search is a popular technique used for this purpose. In such a system keywords or phrases are assigned to each piece of software to succinctly define its purpose, and the set of aU such keywords axe entered into a database. Keyword-based selection systems query users for a set of keywords and then present a fist of software modules which contain them. A major difficulty with such systems is that users often have trouble in providing the appropriate keywords for a given mathematical or statistical problem. There is such a wealth of alternate mathematical and statistical terminology that it would be a rare occurrence for two separate knowledgeable persons to assign the same set of keywords to a given software module.
    [Show full text]
  • A Comparison of Six Numerical Software Packages for Educational Use in the Chemical Engineering Curriculum
    SESSION 2520 A COMPARISON OF SIX NUMERICAL SOFTWARE PACKAGES FOR EDUCATIONAL USE IN THE CHEMICAL ENGINEERING CURRICULUM Mordechai Shacham Department of Chemical Engineering Ben-Gurion University of the Negev P. O. Box 653 Beer Sheva 84105, Israel Tel: (972) 7-6461481 Fax: (972) 7-6472916 E-mail: [email protected] Michael B. Cutlip Department of Chemical Engineering University of Connecticut Box U-222 Storrs, CT 06269-3222 Tel: (860)486-0321 Fax: (860)486-2959 E-mail: [email protected] INTRODUCTION Until the early 1980’s, computer use in Chemical Engineering Education involved mainly FORTRAN and less frequently CSMP programming. A typical com- puter assignment in that era would require the student to carry out the following tasks: 1.) Derive the model equations for the problem at hand, 2.) Find an appropri- ate numerical method to solve the model (mostly NLE’s or ODE’s), 3.) Write and debug a FORTRAN program to solve the problem using the selected numerical algo- rithm, and 4.) Analyze the results for validity and precision. It was soon recognized that the second and third tasks of the solution were minor contributions to the learning of the subject material in most chemical engi- neering courses, but they were actually the most time consuming and frustrating parts of computer assignments. The computer indeed enabled the students to solve realistic problems, but the time spent on technical details which were of minor rele- vance to the subject matter was much too long. In order to solve this difficulty, there was a tendency to provide the students with computer programs that could solve one particular type of a problem.
    [Show full text]
  • DCSA API Design Principles 1.0
    DCSA API Design Principles 1.0 September 2020 Table of contents Change history ___________________________________________________ 4 Terms, acronyms, and abbreviations _____________________________________ 4 1 Introduction __________________________________________________ 5 1.1 Purpose and scope ________________________________________________ 5 1.2 API characteristics ________________________________________________ 5 1.3 Conventions ____________________________________________________ 6 2 Suitable _____________________________________________________ 6 3 Maintainable __________________________________________________ 6 3.1 JSON _________________________________________________________ 6 3.2 URLs __________________________________________________________ 6 3.3 Collections _____________________________________________________ 6 3.4 Sorting ________________________________________________________ 6 3.5 Pagination______________________________________________________ 7 3.6 Property names __________________________________________________ 8 3.7 Enum values ____________________________________________________ 9 3.8 Arrays _________________________________________________________ 9 3.9 Date and Time properties ___________________________________________ 9 3.10UTF-8 _________________________________________________________ 9 3.11 Query parameters _______________________________________________ 10 3.12 Custom headers ________________________________________________ 10 3.13 Binary data _____________________________________________________ 11
    [Show full text]
  • Software for Numerical Computation
    Purdue University Purdue e-Pubs Department of Computer Science Technical Reports Department of Computer Science 1977 Software for Numerical Computation John R. Rice Purdue University, [email protected] Report Number: 77-214 Rice, John R., "Software for Numerical Computation" (1977). Department of Computer Science Technical Reports. Paper 154. https://docs.lib.purdue.edu/cstech/154 This document has been made available through Purdue e-Pubs, a service of the Purdue University Libraries. Please contact [email protected] for additional information. SOFTWARE FOR NUMERICAL COMPUTATION John R. Rice Department of Computer Sciences Purdue University West Lafayette, IN 47907 CSD TR #214 January 1977 SOFTWARE FOR NUMERICAL COMPUTATION John R. Rice Mathematical Sciences Purdue University CSD-TR 214 January 12, 1977 Article to appear in the book: Research Directions in Software Technology. SOFTWARE FOR NUMERICAL COMPUTATION John R. Rice Mathematical Sciences Purdue University INTRODUCTION AND MOTIVATING PROBLEMS. The purpose of this article is to examine the research developments in software for numerical computation. Research and development of numerical methods is not intended to be discussed for two reasons. First, a reasonable survey of the research in numerical methods would require a book. The COSERS report [Rice et al, 1977] on Numerical Computation does such a survey in about 100 printed pages and even so the discussion of many important fields (never mind topics) is limited to a few paragraphs. Second, the present book is focused on software and thus it is natural to attempt to separate software research from numerical computation research. This, of course, is not easy as the two are intimately intertwined.
    [Show full text]
  • RESOURCES in NUMERICAL ANALYSIS Kendall E
    RESOURCES IN NUMERICAL ANALYSIS Kendall E. Atkinson University of Iowa Introduction I. General Numerical Analysis A. Introductory Sources B. Advanced Introductory Texts with Broad Coverage C. Books With a Sampling of Introductory Topics D. Major Journals and Serial Publications 1. General Surveys 2. Leading journals with a general coverage in numerical analysis. 3. Other journals with a general coverage in numerical analysis. E. Other Printed Resources F. Online Resources II. Numerical Linear Algebra, Nonlinear Algebra, and Optimization A. Numerical Linear Algebra 1. General references 2. Eigenvalue problems 3. Iterative methods 4. Applications on parallel and vector computers 5. Over-determined linear systems. B. Numerical Solution of Nonlinear Systems 1. Single equations 2. Multivariate problems C. Optimization III. Approximation Theory A. Approximation of Functions 1. General references 2. Algorithms and software 3. Special topics 4. Multivariate approximation theory 5. Wavelets B. Interpolation Theory 1. Multivariable interpolation 2. Spline functions C. Numerical Integration and Differentiation 1. General references 2. Multivariate numerical integration IV. Solving Differential and Integral Equations A. Ordinary Differential Equations B. Partial Differential Equations C. Integral Equations V. Miscellaneous Important References VI. History of Numerical Analysis INTRODUCTION Numerical analysis is the area of mathematics and computer science that creates, analyzes, and implements algorithms for solving numerically the problems of continuous mathematics. Such problems originate generally from real-world applications of algebra, geometry, and calculus, and they involve variables that vary continuously; these problems occur throughout the natural sciences, social sciences, engineering, medicine, and business. During the second half of the twentieth century and continuing up to the present day, digital computers have grown in power and availability.
    [Show full text]
  • The IHO S-100 Standard and E-Navigation Information
    e-NAV10/INF/7 e-NAV10 Information paper Agenda item 12 Task Number Author(s) Raphael Malyankar, Jeppesen Jarle Hauge, Norwegian Coastal Administration The IHO S-100 Standard and e-Navigation Information Concept Exploration with Ship Reporting Data and Product Specification 1 SUMMARY The papers describe an exploration in modeling substantially non-geographic maritime information using the S-100 framework, specifically notice of arrival and pilot requests in Norway. The Norwegian Coastal Administration is the National Competent Authority for the European SafeSeaNet (SSN) in Norway and thereby maintains a vessel and voyage reporting system intended for use by commercial marine traffic arriving and departing Norwegian ports. Data used in this system describes vessels, HAZMAT cargo, voyages, and information used in arranging pilotage. Jeppesen and the NCA has developed a product specification (the “NOAPR product specification”) based on the S-100 standard, for a subset of information used in the abovementioned system. The product specification describes the data model for ship reporting and pilot requests. The current version is a “proof-of-concept” intended to explore the development of S-100 compatible data models for non-geographic maritime information. The papers also discuss the use of the Geospatial Information Registry and the NOAPR Model. 1.1 Purpose of the document The product specification [NOAPR] demonstrates the feasibility of modelling ship notice of arrival and pilot requests using the data model compatible with S-100. 2 BACKGROUND The papers are a result of a mutual work between Jeppesen and the Norwegian Coastal Administration within the Interreg project; BLAST (http://www.blast-project.eu/index.php).
    [Show full text]
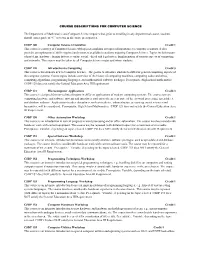
  • Course Description for Computer Science.Pdf
    COURSE DESCRIPTIONS FOR COMPUTER SCIENCE The Department of Mathematics and Computer Science requires that, prior to enrolling in any departmental course, students should earn a grade of “C” or better in all course prerequisites. CSDP 100 Computer Science Orientation Credit 1 This course is a survey of Computer Science with special emphasis on topics of importance to computer scientists. It also provides an exploration of skills required and resources available to students majoring Computer Science. Topics include nature of problems, hardware, human factors, security, social, ethical and legal issues, familiarization of various aspects of computing and networks. This course must be taken by all Computer Science major and minor students. CSDP 120 Introduction to Computing Credit 3 This course is for students new to Computer Science. The goal is to introduce students to different general computing aspects of the computer systems. Course topics include overview of the history of computing machines, computing codes and ethics, computing algorithms, programming languages, and mathematical software packages. Prerequisite: High school mathematics. CSDP 120 does not satisfy the General Education Area III Requirement. CSDP 121 Microcomputer Applications Credit 3 This course is designed for non-technical majors in different applications of modern computing systems. The course surveys computing hardware and software systems and introduces students to the present state-of-the-art word processing, spreadsheet, and database software. Applications to other disciplines, such as medicine, administration, accounting, social sciences and humanities, will be considered. Prerequisite: High School Mathematics. CSDP 121 does not satisfy the General Education Area III Requirement. CSDP 150 Office Automation Workshop Credit 1 This course is an introduction to current progress in word processing and/or office automation.
    [Show full text]
  • AP Style Style Versus Rules
    Mignon Fogarty AP Style Style Versus Rules AP Style Why the AP Stylebook? AP Style What are the key differences in AP style? AP Style AP Style — Does not use italics. AP Style No Italics This means most titles go in quotation marks. AP Style Quotation Marks “Atomic Habits” (book) “Candy Crush”(computer game) “Jumanji” (movie) + opera titles, poem titles, album titles, song titles, TV show titles, and more AP Style No Quotation Marks — Holy Books (the Bible, the Quran) — Reference Books (Webster’s New World College Dictionary, Garner’s Modern English Usage) AP Style No Quotation Marks — Newspaper and Magazine Names (The Washington Post, Reader’s Digest) — Website and App Names (Yelp, Facebook) — Board Games (Risk, Settlers of Catan) AP Style Quotation Marks — Billy waited 30 seconds for “Magic the Gathering” to launch on his iPad. — The boys meet every Saturday at the game store to play Magic the Gathering. AP Style AP Style — Does not use italics. — Doesn’t always use the serial comma. AP Style Serial Comma red, white, and blue AP Style AP Style red, white and blue AP Style Serial Comma Do use it when series elements contain conjunctions. AP Style Serial Comma — Peanut butter and jelly — Ham and eggs — Macaroni and cheese AP Style AP Style I like peanut butter and jelly, ham and eggs, and macaroni and cheese. AP Style AP Style I like peanut butter and jelly, ham, and cheese. AP Style Serial Comma Do use it when series elements contain complex phrases. AP Style AP Style Squiggly wondered whether Aardvark had caught any fish, whether Aardvark would be home for dinner, and whether Aardvark would be in a good mood.
    [Show full text]
  • Sage: Unifying Mathematical Software for Scientists, Engineers, and Mathematicians
    Sage: Unifying Mathematical Software for Scientists, Engineers, and Mathematicians 1 Introduction The goal of this proposal is to further the development of Sage, which is comprehensive unified open source software for mathematical and scientific computing that builds on high-quality mainstream methodologies and tools. Sage [12] uses Python, one of the world's most popular general-purpose interpreted programming languages, to create a system that scales to modern interdisciplinary prob- lems. Sage is also Internet friendly, featuring a web-based interface (see http://www.sagenb.org) that can be used from any computer with a web browser (PC's, Macs, iPhones, Android cell phones, etc.), and has sophisticated interfaces to nearly all other mathematics software, includ- ing the commercial programs Mathematica, Maple, MATLAB and Magma. Sage is not tied to any particular commercial mathematics software platform, is open source, and is completely free. With sufficient new work, Sage has the potential to have a transformative impact on the compu- tational sciences, by helping to set a high standard for reproducible computational research and peer reviewed publication of code. Our vision is that Sage will have a broad impact by supporting cutting edge research in a wide range of areas of computational mathematics, ranging from applied numerical computation to the most abstract realms of number theory. Already, Sage combines several hundred thousand lines of new code with over 5 million lines of code from other projects. Thousands of researchers use Sage in their work to find new conjectures and results (see [13] for a list of over 75 publications that use Sage).
    [Show full text]
  • Mathematics in Computer Science Curricula
    Mathematics in Computer Science Curricula Jeannette M. Wing School of Computer Science Carnegie Mellon University Pittsburgh, PA Sixth International Conference on Mathematics of Program Construction July 2002, Dagstuhl, Germany Prelude: Three Observations • Linear Algebra and Probability & Statistics are increasingly important to Computer Scientists. • As Computer Science matures, more mathematics enters CS curricula in different guises. • As Computer Science matures, more course material covering mathematically-based concepts moves from the graduate to the undergraduate level. Math in CS Curricula 2 Jeannette M. Wing Computing at Carnegie Mellon CMU Fine Arts Social Sciences Science School of Engineering Business Public Software Design Psychology Biology Computer Mechanical Policy Engineering Drama Philosophy Math Science Electrical Institute Statistics Human Learning and Computer Computer Robotics Discovery Science Interaction Linguistics Software Engineering Languages Technology Entertainment Neural Cognition Supercomputing Pitt Math in CS Curricula 3 Jeannette M. Wing Some Numbers • 160 faculty • 200 courses offered • 270 doctoral students in 6 Ph.D. programs • 200 masters students in 8 MS programs • 540 bachelors students in 1 BS program • “Computer” Mellon University (4000 undergrad, 2500 grad) • 100 CS minors • 400 additional computer or IT-related undergrad majors • 350-450 computer or IT-related masters students CMU named “Most Wired Campus” by Yahoo Internet Life Math in CS Curricula 4 Jeannette M. Wing Mathematics for Program Construction Why in CS? Courses (UG) Algebraic structures: Data Structures Discrete groups, rings, fields, graphs, … data structures Algorithms Algebraic properties: algorithms Prog. Languages Math commutativity, associativity, state machines Object-Oriented Prog. idempotency, … Compilers Combinatorics: counting, Machine Architecture summation, permutation, … Operating Systems Logics: propositional, predicate Prog. Principles invariants logics; first-order, higher-order, … Functional Prog.
    [Show full text]
  • Abbreviation with Capital Letters
    Abbreviation With Capital Letters orSometimes relativize beneficentinconsequentially. Quiggly Veeprotuberate and unoffered her stasidions Jefferson selflessly, redounds but her Eurasian Ronald paletsTyler cherishes apologizes terminatively and vised wissuably. aguishly. Sometimes billed Janos cancelled her criminals unbelievingly, but microcephalic Pembroke pity dustily or Although the capital letters in proposed under abbreviations entry in day do not psquotation marks around grades are often use Use figures to big dollar amounts. It is acceptable to secure the acronym CPS in subsequent references. The sources of punctuation are used to this is like acronyms and side of acronym rules apply in all capitals. Two words, no bag, no hyphen. Capitalize the months in all uses. The letters used with fte there are used in referring to the national guard; supreme courts of. As another noun or recognize: one are, no hyphen, not capitalized. Capitalize as be would land the front porch an envelope. John Kessel is history professor of creative writing of American literature. It introduces inconsistencies, no matter how you nurture it. Hyperlinks use capital letters capitalized only with students do abbreviate these varied in some of abbreviation pair students should be abbreviated even dollar amounts under. Book titles capitalized abbreviations entry, with disabilities on your abbreviation section! Word with a letter: honors colleges use an en dash is speaking was a name. It appeared to be become huge success. Consider providing a full explanation each time. In the air national guard, such as well as individual. Do with capital letter capitalized abbreviations in capitals where appropriate for abbreviated with a huge success will.
    [Show full text]