DOCSLIB.ORG

Fermat Point

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fermat Point Fermat Point The segments joining each F vertex of any triangle with the remote vertex of the equilateral triangle drawn D A externally on the L opposite side are concurrent, K O C B M Proof : Circles K and L meet at points O and A. Since ADC = 240 and 1 1 ∠AOC = ADC , ∠AOC = 120 , Similarly, ∠AOB = AFB = 120, 2 2 ∴ ∠COB = 120 (because a complete revolution is 360 degrees). Because CEB = 240 , ∠COB is an inscribed angle and point O must lie on circle M. Therefore, the three circles are concurrent, intersecting at point O. Now, join point O with points A, B, C, D, E, and F. ∠DOA = ∠AOF = ∠FOB = 60 , and therefore DOB . Similarly, COF and AOE . Therefore DB, AE, and CF are concurrent, intersecting at O ( which is also a point of intersection of circles K, L, and M. ) F LEMMA: (for Napoleon’s Theorem) D The segments joining each A vertex of any triangle L with the remote vertex K of the equilateral triangle drawn O externally on the opposite side are congruent, C B M Proof : Since ∠DCA = ∠ECB = 60 , ∠DCB = ∠ACE (addition). Also, DC = AC and CB = CE , Therefore, DCB ≅ ACE and DB = AE . In a similar manner, we can show EBA ≅ CBF ⇒ AE = CF . Thus DB = AE = CF . Napoleon’s Theorem The circumcenters of the three equilateral triangles drawn externally on the sides of a given triangle determine an equilateral triangle. L A K B D O C M Proof : E Consider DAC . AK is two thirds the length of the altitude (or median). Using AC 3 the relationships in a 30-60-90 triangle = , Similarly AK 1 AF 3 AC AF in AFB, = . ∴ = . Since ∠KAC = ∠LAF = 30 , ∠CAL = ∠CAL , AL 1 AK AL and ∠KAL = ∠CAF (addition), we have KAL CAF . Therefore, CF CA 3 = = . KL AK 1 DB 3 AE 3 DB AE CF Similarly, = and = . ∴ = = . But since KM 1 ML 1 KM ML KL DB = AE = CF , we have KM = ML = KL or KML is equilateral. Menelaus’ Theorem Q A Q A N N P M P M R R B L B L C C Q A N P M R B L A set of 3 points located on each of the 3 sides. C In any triangle, the Menelaus points are collinear if and only if AN / NB x BL / LC x CM / MA = -1 . Proof : From similar triangles . AN AP BL QB CM RC = , = , and = NB QB LC CR MA AP By multiplication, we get A N AN BL CM ⋅ ⋅ = − 1 NB LC MA M B L C Conversely, let the line containing N and L intersect AC at M ′ . Using the AN BL CM ′ converse just proved , we know that ⋅ ⋅ = − 1, But by hypothesis, NB LC M ′A AN BL CM CM ′ CM ⋅ ⋅ = − 1 . ∴ = which indicates that M ′ = M . This proves NB LC MA M ′A MA collinearity. (Gerard) Desargues’s Theorem P A C B M L N C' B' are in “PERSPECTIVE” Copolar if AA', BB', and CC' are concurrent. Coaxial if intersection points of BC and A' B'C', CA and C'A', and AB and A'B' are collinear. If the triangles ABC and A’B’C’ are so situated that AA’, BB’, and CC’ are concurrent at P; and if BC and B’C’ meet at N, AB and A’B’ meet at M, and AC and A’C’ meet in L, then K, L, and M are collinear and conversely. Copolar triangles are coaxial, and conversely. Proof : Consider NBC to be a transversal of PB′C′ . Then by Menelaus’ Theorem PB NB′ CC′ ⋅ ⋅ = −1. Similarly, considering MBA to be a transversal of PB′A′ BB′ NC′ CP PA A′M B′B we have ⋅ ⋅ = −1 . Now taking LAC to be a transversal of PA′C′ AA′ MB′ BP PC C′L A′A we have ⋅ ⋅ = −1. Multiplying we get CC′ LA′ AP B′N A′M C′L ⋅ ⋅ = −1 NC′ MB′ LA′ If the triangles ABC and A’B’C’ are in perspective, the points of intersection of the corresponding sides are collinear; and conversely, if the points of intersection of the corresponding sides are collinear, the triangles are in perspective. L A' A M C C' O B B' N L A' A M C C' O B B' N Proof of Converse: Let N, M and L be collinear and consider AA′N and BB′M . These triangles are in perspective with L as center of perspective. Moreover, O, C and C′ are the points of intersection of their pairs of corresponding sides. Hence these points are collinear. Pascal’s Theorem N F E Y D M C L A B X Z The points of intersection of the opposite sides of an inscribed hexagon are collinear. ( Any conic ! ) Proof : Consider XYZ whose vertices are the points of intersection of AB and CD , CD and EF , and EF and AB , respectively, and consider DE, FA and BC as transversals cutting the sides of XYZ . BY applying Menelaus’ Theorem we have the following relations: XL ZE YD YN XA ZF ZM YC XB ⋅ ⋅ = − 1; ⋅ ⋅ = − 1 ; ⋅ ⋅ = − 1. LZ EY DX NX AZ FY MY CX BZ Taking the products of the three right members and the three left members, and rearranging the ratios, XL ZM YN ZE ⋅ZF XB⋅ XA YC ⋅YD ⋅ ⋅ ⋅ ⋅ ⋅ = − 1 LZ MY NX ZB⋅ZA XC ⋅XD YE⋅YF Now each of the last three fractions in this product equals 1, we have XL ZM YN ⋅ ⋅ = − 1 and thus L, M, and N are collinear. LZ MY NX (Charles-Julien) Brianchon’s Theorem D E d e c F f O C b a A B If a hexagon is circumscribed about a circle, the diagonals joining opposite vertices are concurrent. Proof : Let ABCDEF be a hexagon circumscribed about a circle. The polars of the vertices A, B, C, D, E, F form the sides of the inscribed polygon whose sides are a, b, c, d, e, f . Since a is a polar of A and d is a polar of D , then the point of intersection of a and d , call it L , is the pole of AD , Likewise, the point of intersection of b and e , call it M , is the pole of BE , And, the point of intersection of c and f , call it N , is the pole of CF , Therefore, by Pascal’s Theorem, L, M , N are collinear, hence their polars AD, BE, CF are concurrent. (Robert) Simson Line C M N B A L P The pedals drawn to the sides of a triangle from any point P on the circumcircle of the triangle are collinear Proof : Draw AP and PB . (We need to prove that ∠MNP + ∠PNL = st. ∠ ). SInce ∠AMP = 90 = ∠ANP , A, P, N and M are concyclic. Also, since ∠PNB = 90 = ∠BLP , P, L, B and N are concyclic. ∠MNP = ∠CBP , each being a supplement of ∠PAM . ∠CBP is the supplement of ∠PBL . But ∠PBL = ∠PNL since PLBN is a cyclic quadrilateral. ∴∠MNP + ∠PNL = st. ∠ and MNL is a straight line. Euler Line A H G O B D A' C P In any triangle, the centroid, orthocenter, and circumcenter are collinear. Proof : Extend OG twice its distance to point H . (We will now show that H is the orthocenter). AHG AOG , since AA′ is divided in a 2:1 ration by G , vertical angle at G , and GH = 2 ⋅OG by construction. This implies AH || OA′ and thus perpendicular to BC . And since we could do the same construction from any vertex without moving the points O, G and H and get the same result, we have shown that the three points lie on a single line. Lemma C C D K P H H S S A C' B A C' B In any traingle, the segment of an altitude from a vertex to the orthocenter is twice the perpendicular from the circumcenter to the same side. Proof : Construct altitude AD and diameter KB intersecting AC at P . SC′ || KA and 1 SC′ = KA . Then CH || KA . Since ∠KCB = 90 and KC || AH ⇒ AHCK is a 2 parallelogram. ∴ CH = KA = 2SC′ (Karl) Feuerbach’s Theorem C R D B' A' E S (The Nine-Point Circle) A circle whose N center is the midpoint of the segment P H Q joining the orthocenter and the circumcenter, and whose radius is A F C' equal to half the radius of the B circumcircle, passes through the feet of the altitudes, the midpoints of the sides, and the midpoints of the segments joining the vertices of the triangle to the orthocenter. Proof : Draw HS and C′R intersecting at N . (We will prove that N is the midpoint of 1 HS and that a circle with center N and a radius of CS will pass through 2 D, E, F, A′, B′, C′, P, Q, R .) 1 1. HR = HC = C′S . Also, HR || C′S . ∴ HC′SR is a parallelogram and 2 HN = NS and C′N = NR . Therefore N is the midpoint of HS . 2. Since ∠C′FR = 90 , a circle with N as center and with radius NR will pass through F, C′, R . 3. CR and SC′ are equal and parallel. Therefore, CRC′S is a parallelogram 1 1 and C′R = SC (a circumradius). ∴ NR = C′R = SC . 2 2 We have proved that N is the midpoint of HS , that the circle with N as center and one half of SC (a circumradius) as a radius passes through a foot of an altitude, F , a midpoint of a side, C′ , and a midpoint of CH, R .
Load more

Recommended publications
  • Projective Geometry: a Short Introduction
    Projective Geometry: A Short Introduction Lecture Notes Edmond Boyer Master MOSIG Introduction to Projective Geometry Contents 1 Introduction 2 1.1 Objective . .2 1.2 Historical Background . .3 1.3 Bibliography . .4 2 Projective Spaces 5 2.1 Definitions . .5 2.2 Properties . .8 2.3 The hyperplane at infinity . 12 3 The projective line 13 3.1 Introduction . 13 3.2 Projective transformation of P1 ................... 14 3.3 The cross-ratio . 14 4 The projective plane 17 4.1 Points and lines . 17 4.2 Line at infinity . 18 4.3 Homographies . 19 4.4 Conics . 20 4.5 Affine transformations . 22 4.6 Euclidean transformations . 22 4.7 Particular transformations . 24 4.8 Transformation hierarchy . 25 Grenoble Universities 1 Master MOSIG Introduction to Projective Geometry Chapter 1 Introduction 1.1 Objective The objective of this course is to give basic notions and intuitions on projective geometry. The interest of projective geometry arises in several visual comput- ing domains, in particular computer vision modelling and computer graphics. It provides a mathematical formalism to describe the geometry of cameras and the associated transformations, hence enabling the design of computational ap- proaches that manipulates 2D projections of 3D objects. In that respect, a fundamental aspect is the fact that objects at infinity can be represented and manipulated with projective geometry and this in contrast to the Euclidean geometry. This allows perspective deformations to be represented as projective transformations. Figure 1.1: Example of perspective deformation or 2D projective transforma- tion. Another argument is that Euclidean geometry is sometimes difficult to use in algorithms, with particular cases arising from non-generic situations (e.g.
    [Show full text]
  • Robot Vision: Projective Geometry
    Robot Vision: Projective Geometry Ass.Prof. Friedrich Fraundorfer SS 2018 1 Learning goals . Understand homogeneous coordinates . Understand points, line, plane parameters and interpret them geometrically . Understand point, line, plane interactions geometrically . Analytical calculations with lines, points and planes . Understand the difference between Euclidean and projective space . Understand the properties of parallel lines and planes in projective space . Understand the concept of the line and plane at infinity 2 Outline . 1D projective geometry . 2D projective geometry ▫ Homogeneous coordinates ▫ Points, Lines ▫ Duality . 3D projective geometry ▫ Points, Lines, Planes ▫ Duality ▫ Plane at infinity 3 Literature . Multiple View Geometry in Computer Vision. Richard Hartley and Andrew Zisserman. Cambridge University Press, March 2004. Mundy, J.L. and Zisserman, A., Geometric Invariance in Computer Vision, Appendix: Projective Geometry for Machine Vision, MIT Press, Cambridge, MA, 1992 . Available online: www.cs.cmu.edu/~ph/869/papers/zisser-mundy.pdf 4 Motivation – Image formation [Source: Charles Gunn] 5 Motivation – Parallel lines [Source: Flickr] 6 Motivation – Epipolar constraint X world point epipolar plane x x’ x‘TEx=0 C T C’ R 7 Euclidean geometry vs. projective geometry Definitions: . Geometry is the teaching of points, lines, planes and their relationships and properties (angles) . Geometries are defined based on invariances (what is changing if you transform a configuration of points, lines etc.) . Geometric transformations
    [Show full text]
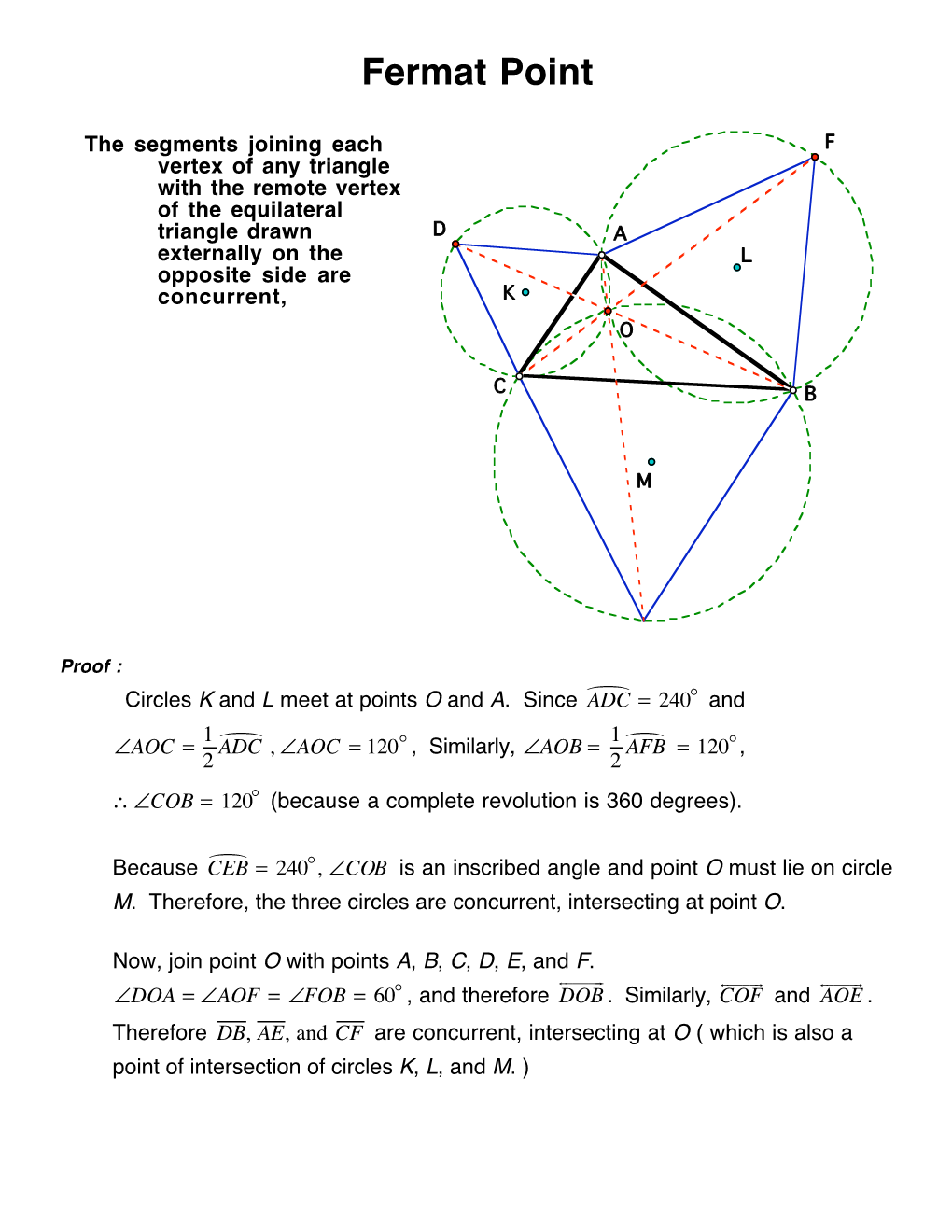
  • Investigating Centers of Triangles: the Fermat Point
    Investigating Centers of Triangles: The Fermat Point A thesis submitted to the Miami University Honors Program in partial fulfillment of the requirements for University Honors with Distinction by Katherine Elizabeth Strauss May 2011 Oxford, Ohio ABSTRACT INVESTIGATING CENTERS OF TRIANGLES: THE FERMAT POINT By Katherine Elizabeth Strauss Somewhere along their journey through their math classes, many students develop a fear of mathematics. They begin to view their math courses as the study of tricks and often seemingly unsolvable puzzles. There is a demand for teachers to make mathematics more useful and believable by providing their students with problems applicable to life outside of the classroom with the intention of building upon the mathematics content taught in the classroom. This paper discusses how to integrate one specific problem, involving the Fermat Point, into a high school geometry curriculum. It also calls educators to integrate interesting and challenging problems into the mathematics classes they teach. In doing so, a teacher may show their students how to apply the mathematics skills taught in the classroom to solve problems that, at first, may not seem directly applicable to mathematics. The purpose of this paper is to inspire other educators to pursue similar problems and investigations in the classroom in order to help students view mathematics through a more useful lens. After a discussion of the Fermat Point, this paper takes the reader on a brief tour of other useful centers of a triangle to provide future researchers and educators a starting point in order to create relevant problems for their students. iii iv Acknowledgements First of all, thank you to my advisor, Dr.
    [Show full text]
  • On the Fermat Point of a Triangle Jakob Krarup, Kees Roos
    280 NAW 5/18 nr. 4 december 2017 On the Fermat point of a triangle Jakob Krarup, Kees Roos Jakob Krarup Kees Roos Department of Computer Science Faculty of EEMCS University of Copenhagen, Denmark Technical University Delft [email protected] [email protected] Research On the Fermat point of a triangle For a given triangle 9ABC, Pierre de Fermat posed around 1640 the problem of finding a lem has been solved but it is not known by 2 point P minimizing the sum sP of the Euclidean distances from P to the vertices A, B, C. whom. As will be made clear in the sec- Based on geometrical arguments this problem was first solved by Torricelli shortly after, tion ‘Duality of (F) and (D)’, Torricelli’s ap- by Simpson in 1750, and by several others. Steeped in modern optimization techniques, proach already reveals that the problems notably duality, however, Jakob Krarup and Kees Roos show that the problem admits a (F) and (D) are dual to each other. straightforward solution. Using Simpson’s construction they furthermore derive a formula Our first aim is to show that application expressing sP in terms of the given triangle. This formula appears to reveal a simple re- of duality in conic optimization yields the lationship between the area of 9ABC and the areas of the two equilateral triangles that solution of (F), straightforwardly. Devel- occur in the so-called Napoleon’s Theorem. oped in the 1990s, the field of conic optimi- zation (CO) is a generalization of the more We deal with two problems in planar geo- Problem (D) was posed in 1755 by well-known field of linear optimization (LO).
    [Show full text]
  • Mathematical Gems
    AMS / MAA DOLCIANI MATHEMATICAL EXPOSITIONS VOL 1 Mathematical Gems ROSS HONSBERGER MATHEMATICAL GEMS FROM ELEMENTARY COMBINATORICS, NUMBER THEORY, AND GEOMETRY By ROSS HONSBERGER THE DOLCIANI MATHEMATICAL EXPOSITIONS Published by THE MArrHEMATICAL ASSOCIATION OF AMERICA Committee on Publications EDWIN F. BECKENBACH, Chairman 10.1090/dol/001 The Dolciani Mathematical Expositions NUMBER ONE MATHEMATICAL GEMS FROM ELEMENTARY COMBINATORICS, NUMBER THEORY, AND GEOMETRY By ROSS HONSBERGER University of Waterloo Published and Distributed by THE MATHEMATICAL ASSOCIATION OF AMERICA © 1978 by The Mathematical Association of America (Incorporated) Library of Congress Catalog Card Number 73-89661 Complete Set ISBN 0-88385-300-0 Vol. 1 ISBN 0-88385-301-9 Printed in the United States of Arnerica Current printing (last digit): 10 9 8 7 6 5 4 3 2 1 FOREWORD The DOLCIANI MATHEMATICAL EXPOSITIONS serIes of the Mathematical Association of America came into being through a fortuitous conjunction of circumstances. Professor-Mary P. Dolciani, of Hunter College of the City Uni­ versity of New York, herself an exceptionally talented and en­ thusiastic teacher and writer, had been contemplating ways of furthering the ideal of excellence in mathematical exposition. At the same time, the Association had come into possession of the manuscript for the present volume, a collection of essays which seemed not to fit precisely into any of the existing Associa­ tion series, and yet which obviously merited publication because of its interesting content and lucid expository style. It was only natural, then, that Professor Dolciani should elect to implement her objective by establishing a revolving fund to initiate this series of MATHEMATICAL EXPOSITIONS.
    [Show full text]
  • The Dual Theorem Concerning Aubert Line
    The Dual Theorem concerning Aubert Line Professor Ion Patrascu, National College "Buzeşti Brothers" Craiova - Romania Professor Florentin Smarandache, University of New Mexico, Gallup, USA In this article we introduce the concept of Bobillier transversal of a triangle with respect to a point in its plan; we prove the Aubert Theorem about the collinearity of the orthocenters in the triangles determined by the sides and the diagonals of a complete quadrilateral, and we obtain the Dual Theorem of this Theorem. Theorem 1 (E. Bobillier) Let 퐴퐵퐶 be a triangle and 푀 a point in the plane of the triangle so that the perpendiculars taken in 푀, and 푀퐴, 푀퐵, 푀퐶 respectively, intersect the sides 퐵퐶, 퐶퐴 and 퐴퐵 at 퐴푚, 퐵푚 and 퐶푚. Then the points 퐴푚, 퐵푚 and 퐶푚 are collinear. 퐴푚퐵 Proof We note that = 퐴푚퐶 aria (퐵푀퐴푚) (see Fig. 1). aria (퐶푀퐴푚) 1 Area (퐵푀퐴푚) = ∙ 퐵푀 ∙ 푀퐴푚 ∙ 2 sin(퐵푀퐴푚̂ ). 1 Area (퐶푀퐴푚) = ∙ 퐶푀 ∙ 푀퐴푚 ∙ 2 sin(퐶푀퐴푚̂ ). Since 1 3휋 푚(퐶푀퐴푚̂ ) = − 푚(퐴푀퐶̂ ), 2 it explains that sin(퐶푀퐴푚̂ ) = − cos(퐴푀퐶̂ ); 휋 sin(퐵푀퐴푚̂ ) = sin (퐴푀퐵̂ − ) = − cos(퐴푀퐵̂ ). 2 Therefore: 퐴푚퐵 푀퐵 ∙ cos(퐴푀퐵̂ ) = (1). 퐴푚퐶 푀퐶 ∙ cos(퐴푀퐶̂ ) In the same way, we find that: 퐵푚퐶 푀퐶 cos(퐵푀퐶̂ ) = ∙ (2); 퐵푚퐴 푀퐴 cos(퐴푀퐵̂ ) 퐶푚퐴 푀퐴 cos(퐴푀퐶̂ ) = ∙ (3). 퐶푚퐵 푀퐵 cos(퐵푀퐶̂ ) The relations (1), (2), (3), and the reciprocal Theorem of Menelaus lead to the collinearity of points 퐴푚, 퐵푚, 퐶푚. Note Bobillier's Theorem can be obtained – by converting the duality with respect to a circle – from the theorem relative to the concurrency of the heights of a triangle.
    [Show full text]
  • The Generalization of Miquels Theorem
    THE GENERALIZATION OF MIQUEL’S THEOREM ANDERSON R. VARGAS Abstract. This papper aims to present and demonstrate Clifford’s version for a generalization of Miquel’s theorem with the use of Euclidean geometry arguments only. 1. Introduction At the end of his article, Clifford [1] gives some developments that generalize the three circles version of Miquel’s theorem and he does give a synthetic proof to this generalization using arguments of projective geometry. The series of propositions given by Clifford are in the following theorem: Theorem 1.1. (i) Given three straight lines, a circle may be drawn through their intersections. (ii) Given four straight lines, the four circles so determined meet in a point. (iii) Given five straight lines, the five points so found lie on a circle. (iv) Given six straight lines, the six circles so determined meet in a point. That can keep going on indefinitely, that is, if n ≥ 2, 2n straight lines determine 2n circles all meeting in a point, and for 2n +1 straight lines the 2n +1 points so found lie on the same circle. Remark 1.2. Note that in the set of given straight lines, there is neither a pair of parallel straight lines nor a subset with three straight lines that intersect in one point. That is being considered all along the work, without further ado. arXiv:1812.04175v1 [math.HO] 11 Dec 2018 In order to prove this generalization, we are going to use some theorems proposed by Miquel [3] and some basic lemmas about a bunch of circles and their intersections, and we will follow the idea proposed by Lebesgue[2] in a proof by induction.
    [Show full text]
  • Linear Features in Photogrammetry
    Linear Features in Photogrammetry by Ayman Habib Andinet Asmamaw Devin Kelley Manja May Report No. 450 Geodetic Science and Surveying Department of Civil and Environmental Engineering and Geodetic Science The Ohio State University Columbus, Ohio 43210-1275 January 2000 Linear Features in Photogrammetry By: Ayman Habib Andinet Asmamaw Devin Kelley Manja May Report No. 450 Geodetic Science and Surveying Department of Civil and Environmental Engineering and Geodetic Science The Ohio State University Columbus, Ohio 43210-1275 January, 2000 ABSTRACT This research addresses the task of including points as well as linear features in photogrammetric applications. Straight lines in object space can be utilized to perform aerial triangulation. Irregular linear features (natural lines) in object space can be utilized to perform single photo resection and automatic relative orientation. When working with primitives, it is important to develop appropriate representations in image and object space. These representations must accommodate for the perspective projection relating the two spaces. There are various options for representing linear features in the above applications. These options have been explored, and an optimal representation has been chosen. An aerial triangulation technique that utilizes points and straight lines for frame and linear array scanners has been implemented. For this task, the MSAT (Multi Sensor Aerial Triangulation) software, developed at the Ohio State University, has been extended to handle straight lines. The MSAT software accommodates for frame and linear array scanners. In this research, natural lines were utilized to perform single photo resection and automatic relative orientation. In single photo resection, the problem is approached with no knowledge of the correspondence of natural lines between image space and object space.
    [Show full text]
  • 1.3 Collinear, Betweenness, and Assumptions Date: Goals: How Are Diagrams Interpreted in the Study of Geometry
    1.3 Collinear, Betweenness, and Assumptions Date: Goals: How are diagrams interpreted in the study of geometry Collinear/Noncollinear: Three or more points that lie on the same line are collinear. Points that do not lie on the same line are noncollinear. Two points are always collinear. For a point to be between two other points, all three points must be collinear. Example 1: Use the diagram to the right to answer the following questions. a. Are points A, B, and C collinear? A Yes, B is between A and C. b. Is point B between A and D? B No, the three points are noncollinear. c. Name 3 noncollinear points. AEC, , and E D C d. Are points A and D collinear? Yes, two points are always collinear. The Triangle Inequality: For any three points, there are only two possibilies: 1. They are collinear. One point must be between the other two. Two of the distances must add to the third. 2. They are noncollinear. The three points will form a triangle. Any two of the lengths will add to be larger than the third. Example 2: If AB=12, BC=13, and AC=25, can we determine if the points are collinear? Yes, the lengths 12 and 13 add to 25, therefore the points are collinear. How to Interpret a Diagram: You Should Assume: You Should Not Assume: Straight lines and angles Right Angles Collinearity of points Congruent Segments Betweenness of points Congruent Angles Relative position of points Relative sizes of segments and angles Example 3: Use the diagram to the right to answer the following questions.
    [Show full text]
  • A Simple Way to Test for Collinearity in Spin Symmetry Broken Wave Functions: General Theory and Application to Generalized Hartree Fock
    A simple way to test for collinearity in spin symmetry broken wave functions: general theory and application to Generalized Hartree Fock David W. Small and Eric J. Sundstrom and Martin Head-Gordon Department of Chemistry, University of California, Berkeley, California 94720 and Chemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720 (Dated: February 17, 2015) Abstract We introduce a necessary and sufficient condition for an arbitrary wavefunction to be collinear, i.e. its spin is quantized along some axis. It may be used to obtain a cheap and simple computa- tional procedure to test for collinearity in electronic structure theory calculations. We adapt the procedure for Generalized Hartree Fock (GHF), and use it to study two dissociation pathways in CO2. For these dissociation processes, the GHF wave functions transform from low-spin Unre- stricted Hartree Fock (UHF) type states to noncollinear GHF states and on to high-spin UHF type states, phenomena that are succinctly illustrated by the constituents of the collinearity test. This complements earlier GHF work on this molecule. 1 I. INTRODUCTION Electronic structure practitioners have long relied on spin-unrestricted Hartree Fock (UHF) and Density Functional Theory (DFT) for open-shell and strongly correlated sys- tems. A key reason for this is that the latter's multiradical nature is partially accommo- dated by unrestricted methods: the paired spin-up and spin-down electrons are allowed to separate, while maintaining their spin alignment along a three-dimensional axis, i.e. their spin collinearity. But, considering the great potential for diversity in multitradical systems, it is not a stretch to concede that this approach is not always reasonable.
    [Show full text]
  • Dissertation Hyperovals, Laguerre Planes And
    DISSERTATION HYPEROVALS, LAGUERRE PLANES AND HEMISYSTEMS { AN APPROACH VIA SYMMETRY Submitted by Luke Bayens Department of Mathematics In partial fulfillment of the requirements For the Degree of Doctor of Philosophy Colorado State University Fort Collins, Colorado Spring 2013 Doctoral Committee: Advisor: Tim Penttila Jeff Achter Willem Bohm Chris Peterson ABSTRACT HYPEROVALS, LAGUERRE PLANES AND HEMISYSTEMS { AN APPROACH VIA SYMMETRY In 1872, Felix Klein proposed the idea that geometry was best thought of as the study of invariants of a group of transformations. This had a profound effect on the study of geometry, eventually elevating symmetry to a central role. This thesis embodies the spirit of Klein's Erlangen program in the modern context of finite geometries { we employ knowledge about finite classical groups to solve long-standing problems in the area. We first look at hyperovals in finite Desarguesian projective planes. In the last 25 years a number of infinite families have been constructed. The area has seen a lot of activity, motivated by links with flocks, generalized quadrangles, and Laguerre planes, amongst others. An important element in the study of hyperovals and their related objects has been the determination of their groups { indeed often the only way of distinguishing them has been via such a calculation. We compute the automorphism group of the family of ovals constructed by Cherowitzo in 1998, and also obtain general results about groups acting on hyperovals, including a classification of hyperovals with large automorphism groups. We then turn our attention to finite Laguerre planes. We characterize the Miquelian Laguerre planes as those admitting a group containing a non-trivial elation and acting tran- sitively on flags, with an additional hypothesis { a quasiprimitive action on circles for planes of odd order, and insolubility of the group for planes of even order.
    [Show full text]
  • Euclidean Versus Projective Geometry
    Projective Geometry Projective Geometry Euclidean versus Projective Geometry n Euclidean geometry describes shapes “as they are” – Properties of objects that are unchanged by rigid motions » Lengths » Angles » Parallelism n Projective geometry describes objects “as they appear” – Lengths, angles, parallelism become “distorted” when we look at objects – Mathematical model for how images of the 3D world are formed. Projective Geometry Overview n Tools of algebraic geometry n Informal description of projective geometry in a plane n Descriptions of lines and points n Points at infinity and line at infinity n Projective transformations, projectivity matrix n Example of application n Special projectivities: affine transforms, similarities, Euclidean transforms n Cross-ratio invariance for points, lines, planes Projective Geometry Tools of Algebraic Geometry 1 n Plane passing through origin and perpendicular to vector n = (a,b,c) is locus of points x = ( x 1 , x 2 , x 3 ) such that n · x = 0 => a x1 + b x2 + c x3 = 0 n Plane through origin is completely defined by (a,b,c) x3 x = (x1, x2 , x3 ) x2 O x1 n = (a,b,c) Projective Geometry Tools of Algebraic Geometry 2 n A vector parallel to intersection of 2 planes ( a , b , c ) and (a',b',c') is obtained by cross-product (a'',b'',c'') = (a,b,c)´(a',b',c') (a'',b'',c'') O (a,b,c) (a',b',c') Projective Geometry Tools of Algebraic Geometry 3 n Plane passing through two points x and x’ is defined by (a,b,c) = x´ x' x = (x1, x2 , x3 ) x'= (x1 ', x2 ', x3 ') O (a,b,c) Projective Geometry Projective Geometry
    [Show full text]