Determining an NHL Center's Value: Salary Prediction Based On
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
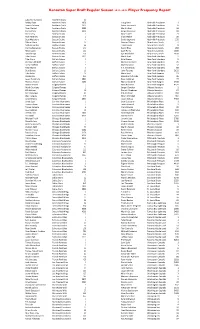
Super Draft Frequency.Xlsx
Kenaston Super Draft Regular Season 2011-2012 Player Frequency Report Lubomir Visnovsky Anaheim Ducks 47 Bobby Ryan Anaheim Ducks 1858 Craig Smith Nashville Predators 1 Teemu Selanne Anaheim Ducks 2410 Patric Hornqvist Nashville Predators 6 Ryan Getzlaf Anaheim Ducks 5089 Martin Erat Nashville Predators 16 Corey Perry Anaheim Ducks 5366 Sergei Kostitsyn Nashville Predators 19 Chris Kelly Boston Bruins 1 Mike Fisher Nashville Predators 21 Rich Peverley Boston Bruins 2 Shea Weber Nashville Predators 26 Brad Marchand Boston Bruins 4 David Legwand Nashville Predators 232 Zdeno Chara Boston Bruins 14 Dainius Zubrus New Jersey Devils 2 Nathan Horton Boston Bruins 60 Travis Zajac New Jersey Devils 8 Patrice Bergeron Boston Bruins 142 Patrik Elias New Jersey Devils 266 Milan Lucic Boston Bruins 144 Zach Parise New Jersey Devils 2189 David Krejci Boston Bruins 150 Ilya Kovalchuk New Jersey Devils 3100 Tyler Seguin Boston Bruins 1011 Mark Streit New York Islanders 2 Tyler Ennis Buffalo Sabres 1 Kyle Okposo New York Islanders 5 Christian Ehrhoff Buffalo Sabres 3 Michael Grabner New York Islanders 25 Drew Stafford Buffalo Sabres 5 Matt Moulson New York Islanders 32 Tyler Myers Buffalo Sabres 9 P.A. Parenteau New York Islanders 58 Brad Boyes Buffalo Sabres 10 John Tavares New York Islanders 5122 Luke Adam Buffalo Sabres 10 Marc Staal New York Rangers 11 Derek Roy Buffalo Sabres 253 Brandon Dubinsky New York Rangers 26 Jason Pominville Buffalo Sabres 2893 Ryan Callahan New York Rangers 77 Thomas Vanek Buffalo Sabres 5280 Marian Gaborik New York Rangers -

NHL Playoffs PDF.Xlsx
Anaheim Ducks Boston Bruins POS PLAYER GP G A PTS +/- PIM POS PLAYER GP G A PTS +/- PIM F Ryan Getzlaf 74 15 58 73 7 49 F Brad Marchand 80 39 46 85 18 81 F Ryan Kesler 82 22 36 58 8 83 F David Pastrnak 75 34 36 70 11 34 F Corey Perry 82 19 34 53 2 76 F David Krejci 82 23 31 54 -12 26 F Rickard Rakell 71 33 18 51 10 12 F Patrice Bergeron 79 21 32 53 12 24 F Patrick Eaves~ 79 32 19 51 -2 24 D Torey Krug 81 8 43 51 -10 37 F Jakob Silfverberg 79 23 26 49 10 20 F Ryan Spooner 78 11 28 39 -8 14 D Cam Fowler 80 11 28 39 7 20 F David Backes 74 17 21 38 2 69 F Andrew Cogliano 82 16 19 35 11 26 D Zdeno Chara 75 10 19 29 18 59 F Antoine Vermette 72 9 19 28 -7 42 F Dominic Moore 82 11 14 25 2 44 F Nick Ritchie 77 14 14 28 4 62 F Drew Stafford~ 58 8 13 21 6 24 D Sami Vatanen 71 3 21 24 3 30 F Frank Vatrano 44 10 8 18 -3 14 D Hampus Lindholm 66 6 14 20 13 36 F Riley Nash 81 7 10 17 -1 14 D Josh Manson 82 5 12 17 14 82 D Brandon Carlo 82 6 10 16 9 59 F Ondrej Kase 53 5 10 15 -1 18 F Tim Schaller 59 7 7 14 -6 23 D Kevin Bieksa 81 3 11 14 0 63 F Austin Czarnik 49 5 8 13 -10 12 F Logan Shaw 55 3 7 10 3 10 D Kevan Miller 58 3 10 13 1 50 D Shea Theodore 34 2 7 9 -6 28 D Colin Miller 61 6 7 13 0 55 D Korbinian Holzer 32 2 5 7 0 23 D Adam McQuaid 77 2 8 10 4 71 F Chris Wagner 43 6 1 7 2 6 F Matt Beleskey 49 3 5 8 -10 47 D Brandon Montour 27 2 4 6 11 14 F Noel Acciari 29 2 3 5 3 16 D Clayton Stoner 14 1 2 3 0 28 D John-Michael Liles 36 0 5 5 1 4 F Ryan Garbutt 27 2 1 3 -3 20 F Jimmy Hayes 58 2 3 5 -3 29 F Jared Boll 51 0 3 3 -3 87 F Peter Cehlarik 11 0 2 2 -

Go Canucks Go!” • Score on Davie (Page 54)
Fevered Fans Luongo and Cory Schneider. Fans are Die-hard Canucks supporters never already breaking out the blue and green stop believing. Their beloved team has face paint and hand-lettering signs in made it to the Stanley Cup finals three anticipation of the season opener Oct. 6 times, and even gone all the way to game against the Pittsburgh Penguins. seven—twice—but has never won the coveted trophy. Local fans remain faithful, Tickets though, already anticipating that lucky With a waitlist for season’s tickets esti- season 41 will see Roberto Luongo, Ryan mated to be up to a decade long, and Kesler, the Sedin twins and all the rest of every game sold out since November the hardworking lads bring Lord Stanley’s 2002, tickets to Canucks games are cup home to its rightful place, within sight harder to find than a Toronto Maple Leafs of the 400-hectare (1,000-acre) park fan in downtown Vancouver—unless you that also bears Stanley’s name. Season know where to look. Visit www.ticket 40 proved to be the most successful so master.ca first. If that ends in a shutout, far, racking up the Presidents’ Trophy for try the Prime Seat Club on canucks.nhl the team, the Art Ross Trophy for Daniel .com. It’s where season’s-ticket hold- Sedin (one year after his identical twin, ers sell off unneeded Henrik, won the honour) and the William M. Jennings Trophy for goalies canucks, ford eRi rad to mark the start of the localB NHLy sh team’s 41st season, we present an intro to the Cks Go! Vancouver's favourite team Go Canu (Opposite, L) Twins Daniel and Henrik Sedin are crowd favourites. -

Team USA Game Notes Vs
Game Notes Media Contacts TEAM USA Dave Fischer 2014 Olympic Winter Games • Sochi, Russia 719.207.5216 or +7 925 007 9283 SVK (0-0-0-0) vs. USA (0-0-0-0) Mike Gilbert Thursday, Feb. 13, 2014 • 4:30 p.m. • Preliminary Round 719.207.5196 or +7 925 007 9286 • TODAY’S GAME -- The U.S. Olympic Men’s Ice Hockey Team opens its preliminary-round schedule in the XXII Olympic Winter Games today 2014 Olympic Winter Games against Slovakia at Shayba Arena. Team USA is the visiting team, will wear Team USA Schedule its white jerseys and occupy the right bench (from the player’s perspective looking onto the ice). Preliminary Round • QUICK TO START -- Jonathan Quick (Milford, Ct./L.A. Kings/UMass) Thursday, Feb. 13 will get the call in goal today. Quick was a member of the 2010 U.S. Slovakia vs. USA (NBCSN) 4:30 p.m./7:30 a.m. Olympic Men’s Ice Hockey Team. He has never played a game for a U.S. team at any level. Quick was a member of the 2010 U.S. Olympic Saturday, Feb. 15 Men’s Ice Hockey Team and did dress for one game (Feb. 18 vs. Russia vs. USA (NBCSN) 4:30 p.m./7:30 a.m. Norway), but did not play. Sunday, Feb. 16 • ALL-TIME vs. SLOVAKIA IN THE OLYMPICS -- The U.S. Olympic Men’s Ice Hockey Team is 0-0-0-1-1 (W-OTW-OTL-L-T) all-time Slovenia vs. USA (NBCSN) 4:30 p.m./7:30 a.m. -

Vancouver Canucks 2009 Playoff Guide
VANCOUVER CANUCKS 2009 PLAYOFF GUIDE TABLE OF CONTENTS VANCOUVER CANUCKS TABLE OF CONTENTS Company Directory . .3 Vancouver Canucks Playoff Schedule. 4 General Motors Place Media Information. 5 800 Griffiths Way CANUCKS EXECUTIVE Vancouver, British Columbia Chris Zimmerman, Victor de Bonis. 6 Canada V6B 6G1 Mike Gillis, Laurence Gilman, Tel: (604) 899-4600 Lorne Henning . .7 Stan Smyl, Dave Gagner, Ron Delorme. .8 Fax: (604) 899-4640 Website: www.canucks.com COACHING STAFF Media Relations Secured Site: Canucks.com/mediarelations Alain Vigneault, Rick Bowness. 9 Rink Dimensions. 200 Feet by 85 Feet Ryan Walter, Darryl Williams, Club Colours. Blue, White, and Green Ian Clark, Roger Takahashi. 10 Seating Capacity. 18,630 THE PLAYERS Minor League Affiliation. Manitoba Moose (AHL), Victoria Salmon Kings (ECHL) Canucks Playoff Roster . 11 Radio Affiliation. .Team 1040 Steve Bernier. .12 Television Affiliation. .Rogers Sportsnet (channel 22) Kevin Bieksa. 14 Media Relations Hotline. (604) 899-4995 Alex Burrows . .16 Rob Davison. 18 Media Relations Fax. .(604) 899-4640 Pavol Demitra. .20 Ticket Info & Customer Service. .(604) 899-4625 Alexander Edler . .22 Automated Information Line . .(604) 899-4600 Jannik Hansen. .24 Darcy Hordichuk. 26 Ryan Johnson. .28 Ryan Kesler . .30 Jason LaBarbera . .32 Roberto Luongo . 34 Willie Mitchell. 36 Shane O’Brien. .38 Mattias Ohlund. .40 Taylor Pyatt. .42 Mason Raymond. 44 Rick Rypien . .46 Sami Salo. .48 Daniel Sedin. 50 Henrik Sedin. 52 Mats Sundin. 54 Ossi Vaananen. 56 Kyle Wellwood. .58 PLAYERS IN THE SYSTEM. .60 CANUCKS SEASON IN REVIEW 2008.09 Final Team Scoring. .64 2008.09 Injury/Transactions. .65 2008.09 Game Notes. 66 2008.09 Schedule & Results. -

Sport-Scan Daily Brief
SPORT-SCAN DAILY BRIEF NHL 10/05/17 Anaheim Ducks Calgary Flames 1076358 Ducks need Rickard Rakell to take center stage as team 1076394 Smith solid, but McDavid leads Oilers past Flames in opens season without Ryan Kesler opener 1076359 Ducks sign Josh Manson to a four-year extension 1076395 Breaking down the deal for Jaromir Jagr 1076360 5 things we learned about the Ducks in training camp 1076396 Flames make it official: Jaromir Jagr will play his 25th 1076361 Miller: Ducks’ Francois Beauchemin hopes to prove it’s season in Calgary worth three-peating 1076397 Francis: Flames hope history doesn't repeat at Rogers 1076362 Ducks ink Josh Manson to four-year extension, add two Place veterans to injured reserve 1076398 Goalie Smith to help Flames stick it to foes 1076399 Flames' Backlund turning heads as one of NHL's best Arizona Coyotes two-way players 1076363 Arizona Coyotes' Rick Tocchet set to lead as the guy he's 1076400 Western Canadian Hamonic fitting in well in Calgary always been 1076401 Francis: Flames season revolves around goaltender Smith 1076364 Coyotes name Ekman-Larsson, Hjalmarsson alternate 1076402 Q & A with Flames star Sean Monahan captains 1076365 What’s new with Coyotes? Coaches, players & Dunkin’ Chicago Blackhawks Donuts 1076403 Blackhawks broadcaster Judd Sirott leaves for Bruins job; 1076366 Questions abound as new era of Coyotes hockey debuts Chris Boden takes over 1076404 I had Blackhawks questions, Stan Bowman had answers, I Boston Bruins still have questions 1076367 Bruins counting on youngsters to play key -
Vancouver Canucks
NATIONAL POST NHL PREVIEW Aquilini Investment Group | Owner Trevor Linden | President of hockey operations General manager Head coach Jim Benning Willie Desjardins $700M 19,770 VP player personnel, ass’t GM Assistant coaches Forbes 2013 valuation Average 2013-14 attendance Lorne Henning Glen Gulutzan NHL rank: Fourth NHL rank: Fifth VP hockey operations, ass’t GM Doug Lidster Laurence Gilman Roland Melanson (goalies) Dir. of player development Ben Cooper (video) Current 2014-15 payroll Stan Smyl Roger Takahashi $66.96M NHL rank: 13th Chief amateur scout (strength and conditioning) Ron Delorme Glenn Carnegie (skills) 2014-15 VANCOUVER CANUCKS YEARBOOK FRANCHISE OUTLOOK RECORDS 2013-14 | 83 points (36-35-11), fifth in Pacific | 2.33 goals per game (28th); 2.53 goals allowed per game (14th) On April 14, with the Vancouver 0.93 5-on-5 goal ratio (21st) | 15.2% power play (26th); 83.2% penalty kill (9th) | +2.4 shot differential per game (8th) GAMES PLAYED, CAREER Canucks logo splashed across the 2013-14 post-season | Did not qualify 1. Trevor Linden | 1988-98, 2001-08 1,140 backdrop behind him, John Tortor- 2. Henrik Sedin | 2000-14 1,010 ella spoke like a man who suspected THE FRANCHISE INDEX: THE CANUCKS SINCE INCEPTION 3. Daniel Sedin | 2000-14 979 the end was near. The beleaguered NUMBER OF NUMBER OF WON STANLEY LOST STANLEY LOCKOUT coach seemed to speak with unusual POINTS WON GAMES PLAYED CUP FINAL CUP FINAL GOALS, CAREER candor, even by his standards, es- 1. Markus Naslund | 1995-2008 346 pecially when asked if the team’s 140 roster needed “freshening.” SEASON CANCELLED 140 2. -

Sabres Keep Vanek by Matching Oilers' $50M Offer - USATODAY.Com
1/29/13 Sabres keep Vanek by matching Oilers' $50M offer - USATODAY.com Cars Auto Financing Event Tickets Jobs Real Estate Online Degrees Business Opportunities Shopping Search How do I find it? Subscribe to paper Become a member of the USA Home News Travel Money Sports Life Tech Weather Log in Sports » NHL Fantasy Mucking and Grinding Team Pages Scores Standings Statistics Schedules Odds/Matchups More Hockey Buffalo Sabres Buy Sabres Tickets Featured video Team report Schedule Salaries Roster Depth chart Player notes Injuries Transactions Statistics Sabres keep Vanek by matching Oilers' $50M offer Royal family Charlie Sheen Updated 7/6/2007 5:16 PM | Comment | Recommend E-mail | Print | Can w edding Actor seeks boost monarchy's custody of tw ins. By Kevin Allen, USA TODAY popularity? More: Video THE VANEK OFFER IN CONTEXT The Buffalo Sabres had seven days to match the Edmonton Oilers' stunning seven-year, $50 million Digg What's this? offer to 23-year-old restricted free agent Thomas There were four major offer sheets to restricted Vanek, but the Sabres didn't even need seven del.icio.us free agents in the last collective-bargaining agreement and one in the current one before minutes to match the offer. New svine Friday's offer by the Edmonton Oilers to the Reddit Buffalo Sabres' Thomas Vanek. A look: "The message is that we aren't going to become a farm team for the other NHL teams," said Buffalo Facebook 1995 - Keith Tkachuk: The Chicago Blackhaw ks general manager Darcy Regier. gave Winnipeg Jets left w ing Keith Tkachuk a What's this? five-year, $17.2 million offer that paid $6 million in the first year. -

2021 Nhl Awards Presented by Bridgestone Information Guide
2021 NHL AWARDS PRESENTED BY BRIDGESTONE INFORMATION GUIDE TABLE OF CONTENTS 2021 NHL Award Winners and Finalists ................................................................................................................................. 3 Regular-Season Awards Art Ross Trophy ......................................................................................................................................................... 4 Bill Masterton Memorial Trophy ................................................................................................................................. 6 Calder Memorial Trophy ............................................................................................................................................. 8 Frank J. Selke Trophy .............................................................................................................................................. 14 Hart Memorial Trophy .............................................................................................................................................. 18 Jack Adams Award .................................................................................................................................................. 24 James Norris Memorial Trophy ................................................................................................................................ 28 Jim Gregory General Manager of the Year Award ................................................................................................. -

How Personal Income Taxes Impact NHL Players, Teams and the Salary Cap
HOME GUEST 0 10 HOME ICE TAX DISADVANTAGE? How personal income taxes impact NHL players, teams and the salary cap Jeff Bowes Research Director Canadian Taxpayers Federation November 2014 The Canadian Taxpayers Federation (CTF) is a federally ABOUT THE incorporated, not-for-profit citizen’s group dedicated to lower taxes, less waste and accountable government. CANADIAN The CTF was founded in Saskatchewan in 1990 when the Association of Saskatchewan Taxpayers and the Resolution TAXPAYERS One Association of Alberta joined forces to create a national taxpayers organization. Today, the CTF has 84,000 FEDERATION supporters nation-wide. The CTF maintains a federal office in Ottawa and regional offices in British Columbia, Alberta, Prairie (SK and MB), Ontario and Atlantic. Regional offices conduct research and advocacy activities specific to their provinces in addition to acting as regional organizers of Canada-wide initiatives. CTF offices field hundreds of media interviews each month, hold press conferences and issue regular news releases, commentaries, online postings and publications to advocate on behalf of CTF supporters. CTF representatives speak at functions, make presentations to government, meet with politicians, and organize petition drives, events and campaigns to mobilize citizens to affect public policy change. Each week CTF offices send out Let’s Talk Taxes commentaries to more than 800 media outlets and personalities across Canada. Any Canadian taxpayer committed to the CTF’s mission is welcome to join at no cost and receive issue and Action Updates. Financial supporters can additionally receive the CTF’s flagship publication,The Taxpayer magazine published four times a year. The CTF is independent of any institutional or partisan affiliations. -

2011 NHL Review Alan Ryder Hockeyanalytics.Com
2011 NHL Review Alan Ryder HockeyAnalytics.com Copyright 2011 2011 NHL Review Page 2 Table of Contents Introduction 3 Player Contribution Basics .................................................................................................. 4 Threshold Performance ...................................................................................................... 5 Situational PC ..................................................................................................................... 6 The Currency of PC ............................................................................................................ 7 Team Performances 9 Goals ................................................................................................................................ 10 Lucky and Unlucky Teams ................................................................................................ 11 Team Success .................................................................................................................. 15 Offense ............................................................................................................................. 16 Shots and Shot Quality ..................................................................................................... 18 Defense ............................................................................................................................ 22 Goaltending ..................................................................................................................... -

Buffalo Sabres Digital Press
Buffalo Sabres Daily Press Clips February 28, 2014 Sharks-Sabres Preview By Nicolino DiBenedetto Associated Press February 28, 2014 The San Jose Sharks picked up where they left off before the Olympic break. Joe Pavelski is glad he didn't. Pavelski looks to build on a hat trick, as the Sharks attempt to beat the last-place Buffalo Sabres for the first time in four years Friday night. San Jose (38-16-6) has won four of five after routing Philadelphia 7-3 on Thursday in its first game in 20 days. The Sharks were outshot 10-5 and trailed 2- 1 after one period before outscoring the Flyers 5-0 in the second. "We didn't have a lot of purpose in our game in the first period, especially in their zone," coach Todd McLellan said. "Kind of skating around waiting for something to happen. We got our forecheck going in the second (and) a lot more pucks to the goaltender, which created second and third chances." Pavelski made his chances count Thursday, scoring on all three of his shots in the second period for his second hat trick of the season. The outburst also came after he had one goal in eight games prior to joining the United States in Sochi. "They were just going in," said Pavelski, who is tied with Toronto's Phil Kessel for second in the league with 32 goals. "Life is good. Hopefully they keep coming." That hasn't been the case against the Sabres (17-34-8), as Pavelski has three goals in seven career meetings and none in the past four.