DOCSLIB.ORG

River Water Quality Zoning: a Case Study of Karoon and Dez River System

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
River Water Quality Zoning: a Case Study of Karoon and Dez River System Iranian J Env Health Sci Eng, 2004, Vol.1, No. 2, pp.16-27 Mohammad Karamou et al: River Water Quality… River Water Quality Zoning: A Case Study of Karoon and Dez River System *M Karamouz 1, N Mahjouri 2, R Kerachian 3 1School of Civil and Environmental Engineering, Amirkabir University, Iran 2 Faculty of Environmental Engineering, University of Tehran, Iran 3Dept. of Civil Engineering, University of Tehran, Iran ABSTRACT Karoon-Dez River basin, with an area of 67000 square kilometers, is located in southern part of Iran. This river system supplies the water demands of 16 cities, several villages, thousands hectares of agricultural lands, and several hydropower plants. The increasing water demands at the project development stage including agricultural networks, fish hatchery projects, and inter-basin water transfers, have caused a gloomy future for water quality of the Karoon and Dez Rivers. A good part of used agricultural water, which is about 8040 million cubic meters, is returned to the rivers through agricultural drainage systems or as non-point, return flows. River water quality zoning could provide essential information for developing river water quality management policies. In this paper, a methodology is presented for this purpose using methods of c -mean crisp classification and a fuzzy clustering scheme. The efficiency of these clustering methods was evaluated using water quality data gathered from the monitoring sampling points along Karoon and Dez Rivers. The results show that the proposed methodology can provide valuable information to support decision-making and to help river water quality management in the region. Keywords: Fuzzy Clustering, Data classification, Water quality zoning, River systems, Karoon, Dez INTRODUCTION water quality control projects. Horton (1965) proposed the first Water Quality There are many similarities between certain Index (WQI). The critical issue in water quality phenomena in the nature. Quantitatively inter- zoning is to construct WQI in a simple way so preting these similarities can make it possible to that the correct information can be extracted categorize the components of a system into dif- from measurements in order to illustrate the ferent classes based on a pre-defined criterion. special and temporal variations (Ott, 1980). One of the main applications of the “clustering Simple weighing method, which is usually used methods” is zoning the river systems based on for water quality zoning, depends on expert various water quality variables. River quality judgments and therefore has been greatly influ- zoning is important in determining the critical enced by human subjectively, even though all zones, optimal locations of the monitoring sta- parameters are carefully measured. In addition, tions and water intakes as well as proposing technical interpretation of WQIs is usually dif- ficult and indexing methods have some weak- *Corresponding author: E-mail: [email protected] Tel: +98 21 664543014, Fax: +98 21 66414213, nesses in explaining a complicated situation. In 16 Mohammad Karamouz et al: River Water Quality… some cases, an expert should check the con- METHODOLOGY centration of all of the water quality variables In this paper, the efficiency of the two well- for water quality explanation and it signifi- known classification methods, namely hard cantly reduces the value of the index methods. c-mean crisp classification and fuzzy clustering Most of the traditional tools for formal model- are evaluated. ing and computing are crisp, deterministic and Hard c-means (HCM) precise in characteristics. Zadeh (1965, 1973) HCM is used to classify data in a crisp sense. In stated that real situations are very often this method, each data point will be assigned to uncertain or vague in a number of ways; he one, and only one, data cluster. A family of sets called this vagueness "fuzziness" and proposed {Ai ,i = 1,2,Lc} as a hard c -partition of set X the Fuzzy Sets Theory. The following constraints After that, many theoretical developments in should be defined. fuzzy logic took place. Now, fuzzy logic affects are applied to these partitions: many disciplines in different fields of study. There is an underlying structure to be under- A1 U A2 ...U Ac = X (1) stood. We often seek to find structure in the A A = i j (2) data obtained from observation such as water i I j quality data provided by a monitoring system. Ai X i (3) Finding the data structure is the essence of clas- 2 c < n (4) sification. In data classification, also termed clustering, the most important issue is deciding Where X = {x ,x ,x ,...,x } is a finite set, what criteria to classify against it. In water 1 2 3 n quality zoning, deviation from water quality comprised of the of data samples, and c is the standard is usually considered as the clustering number of partitions or clusters, in which the criteria. data will be classified. Where c = n , classes Classical (crisp) clustering algorithms generate just places each data sample into its own class, different clusters so that each object is assigned and c = 1 places all data samples into the same to exactly one cluster. However, in many cases, class; neither case requires any effort in classi- objects cannot adequately be assigned to strictly fication and both are intrinsically uninteresting. one cluster because they are located between Equation 1 expresses the fact that the set of all clusters. In such a case, fuzzy clustering classes exhaust the universe of data samples. method may provide clusters that are more re- Equation 2 indicates that none of the classes alistic by assigning overlapping membership overlaps in the sense that a data sample can functions. Kung et al. (1992) proposed a water belong to more than one class. Equation 3 quality index for water quality assessment and simply expresses that a class cannot be empty showed that fuzzy clustering analysis might be and it cannot contain all the data samples. used as a complement or an alternative to Within all the possible c -partitions for n data common quantitative methods in water quality samples, the most reasonable c partition should assessment, especially when WQI scores are be selected. A within-class sum of squared er- close to the thresholds between normal and ab- rors approach using Euclidean norm to charac- normal condition. In this paper, the main char- terize distance, is used in c -mean clustering. In acteristics of crisp and fuzzy clustering methods this approach, Euclidean distance is measured th th and their suitability for river water quality between the k data sample xk and i cluster zoning are presented and the efficiency of the- center v~ by the following expression (Ross, ses methods are evaluated using water quality i 1997): data of Karoon-Dez River system. 17 Iranian J Env Health Sci Eng, 2004, Vol.1, No. 2, pp.16-27 0.5 m Symmetry µR(xi ,xj )=µR(xj ,xi ) (11) ~ 2 d ik = xk − vi = ∑ ()xkj − vij (5) j=1 Transitivity Since each data sample requires m coordinates µR (xi , x j ) = !1 and µR (x j, xk ) = !2 " µR (xi , xk ) = to describe its location in m dimensional space, ! where ! min[! ,! ] each cluster center also requires m coordinates 1 2 to describe its location in this same place. th Therefore, the i cluster center is a vector of (12) length m as: In which, µ R (xi ,x j ) is the membership func- tion of the fuzzy relation R , which shows the v~ = {v ,v ,...,v } (6) i i1 i2 im similarity of, x and x . When there are several i j criteria in evaluating the similarity of some Where the j th coordinate is calculated by: elements, fuzzy relation can be presented by a similarity matrix. Many investigators have pro- n posed several similarity matrices. For example, χ .x ∑k =1 ik kj Wang (1983) proposed the following similarity v = (7) ij n matrix: χ ∑k =1 ik 1 x j ∈Ai p χij = (8) ∑ (x .x ) 0 x ∉A ik jk j i k =1 p rij = + i ≠ j p p p p ∑ (x .x ). ∑ (x .x ) ∑ (x .x )− ∑ (x .x ) ik ik jk ik ik ik jk ik The optimum partitions that are selected pro- k =1 k =1 i =1 i =1 duce the minimum value for the following (13) objective function. n c 2 rij = M ≥ Max (rij ∀i ≠ j) i ≠ j (14) Min z = ∑∑χ ik ()d ik (9) k ==1 i 1 th Where, rij is ij element of the similarity Fuzzy clustering using equivalence relation. matrix, x is the value of k th criterion for In fuzzy clustering, to classify data points using ik fuzzy relations, we need to find the associated element i , and p is equal to the number of fuzzy equivalence relation. A fuzzy relation, on criteria such as water quality indicators. a single set X is also a relation from X to X . According to this formula, the value of the It is a fuzzy equivalence relation if all of the diagonal of the new matrix should be greater following three properties for matrix relation than the greatest element of the matrix. can be applied: In most real cases, the fuzzy relation being established is not stabilized; it meets the Reflexivity µ R (xi ,xi ) 1= (10) reflexivity and symmetry requirements, but not the transitivity. Thus, the fuzzy relation has to 18 Mohammad Karamouz et al: River Water Quality… be transformed before it can become part of a Based on different values of ! cuts, we can clustering chart. This transformation can be classify the data as illustrated in Table 1 and done through a Max-Min self-multiply Fig 1. processing of fuzzy matrix that is: The main five steps in river water quality zon- ing using fuzzy clustering analysis are as fol- rij = V( rik # rjk ) (15) lows: a) Selection the clustering criteria Where V is the maximum operator and F is the In river water quality zoning, the clustering minimum operator; rij represents the element of criteria are usually the concentration of indica- th th the i row and the j column in the similarity tor water quality variables.
Load more

Recommended publications
  • Sand Dune Systems in Iran - Distribution and Activity
    Sand Dune Systems in Iran - Distribution and Activity. Wind Regimes, Spatial and Temporal Variations of the Aeolian Sediment Transport in Sistan Plain (East Iran) Dissertation Thesis Submitted for obtaining the degree of Doctor of Natural Science (Dr. rer. nat.) i to the Fachbereich Geographie Philipps-Universität Marburg by M.Sc. Hamidreza Abbasi Marburg, December 2019 Supervisor: Prof. Dr. Christian Opp Physical Geography Faculty of Geography Phillipps-Universität Marburg ii To my wife and my son (Hamoun) iii A picture of the rock painting in the Golpayegan Mountains, my city in Isfahan province of Iran, it is written in the Sassanid Pahlavi line about 2000 years ago: “Preserve three things; water, fire, and soil” Translated by: Prof. Dr. Rasoul Bashash, Photo: Mohammad Naserifard, winter 2004. Declaration by the Author I declared that this thesis is composed of my original work, and contains no material previously published or written by another person except where due reference has been made in the text. I have clearly stated the contribution by others to jointly-authored works that I have included in my thesis. Hamidreza Abbasi iv List of Contents Abstract ................................................................................................................................................. 1 1. General Introduction ........................................................................................................................ 7 1.1 Introduction and justification ........................................................................................................
    [Show full text]
  • Review and Updated Checklist of Freshwater Fishes of Iran: Taxonomy, Distribution and Conservation Status
    Iran. J. Ichthyol. (March 2017), 4(Suppl. 1): 1–114 Received: October 18, 2016 © 2017 Iranian Society of Ichthyology Accepted: February 30, 2017 P-ISSN: 2383-1561; E-ISSN: 2383-0964 doi: 10.7508/iji.2017 http://www.ijichthyol.org Review and updated checklist of freshwater fishes of Iran: Taxonomy, distribution and conservation status Hamid Reza ESMAEILI1*, Hamidreza MEHRABAN1, Keivan ABBASI2, Yazdan KEIVANY3, Brian W. COAD4 1Ichthyology and Molecular Systematics Research Laboratory, Zoology Section, Department of Biology, College of Sciences, Shiraz University, Shiraz, Iran 2Inland Waters Aquaculture Research Center. Iranian Fisheries Sciences Research Institute. Agricultural Research, Education and Extension Organization, Bandar Anzali, Iran 3Department of Natural Resources (Fisheries Division), Isfahan University of Technology, Isfahan 84156-83111, Iran 4Canadian Museum of Nature, Ottawa, Ontario, K1P 6P4 Canada *Email: [email protected] Abstract: This checklist aims to reviews and summarize the results of the systematic and zoogeographical research on the Iranian inland ichthyofauna that has been carried out for more than 200 years. Since the work of J.J. Heckel (1846-1849), the number of valid species has increased significantly and the systematic status of many of the species has changed, and reorganization and updating of the published information has become essential. Here we take the opportunity to provide a new and updated checklist of freshwater fishes of Iran based on literature and taxon occurrence data obtained from natural history and new fish collections. This article lists 288 species in 107 genera, 28 families, 22 orders and 3 classes reported from different Iranian basins. However, presence of 23 reported species in Iranian waters needs confirmation by specimens.
    [Show full text]
  • Rare Birds in Iran in the Late 1960S and 1970S
    Podoces, 2008, 3(1/2): 1–30 Rare Birds in Iran in the Late 1960s and 1970s DEREK A. SCOTT Castletownbere Post Office, Castletownbere, Co. Cork, Ireland. Email: [email protected] Received 26 July 2008; accepted 14 September 2008 Abstract: The 12-year period from 1967 to 1978 was a period of intense ornithological activity in Iran. The Ornithology Unit in the Department of the Environment carried out numerous surveys throughout the country; several important international ornithological expeditions visited Iran and subsequently published their findings, and a number of resident and visiting bird-watchers kept detailed records of their observations and submitted these to the Ornithology Unit. These activities added greatly to our knowledge of the status and distribution of birds in Iran, and produced many records of birds which had rarely if ever been recorded in Iran before. This paper gives details of all records known to the author of 92 species that were recorded as rarities in Iran during the 12-year period under review. These include 18 species that had not previously been recorded in Iran, a further 67 species that were recorded on fewer than 13 occasions, and seven slightly commoner species for which there were very few records prior to 1967. All records of four distinctive subspecies are also included. The 29 species that were known from Iran prior to 1967 but not recorded during the period under review are listed in an Appendix. Keywords: Rare birds, rarities, 1970s, status, distribution, Iran. INTRODUCTION Eftekhar, E. Kahrom and J. Mansoori, several of whom quickly became keen ornithologists.
    [Show full text]
  • Karim Dahimi Place of Birth
    Page 1 of 15 Witness Statement of Karim Dahimi Witness Statement of Karim Dahimi Name: Karim Dahimi Place of Birth: Ahvaz, Iran Date of Birth: September 23, 1971 Occupation: Teacher Interviewing Organization: Iran Human Rights Documentation Center (IHRDC) Date of Interview: September 25, 2012 Interviewer: IHRDC Staff This statement was prepared pursuant to an interview with Karim Dahimi. It was approved by Karim Dahimi on September 25, 2013. There are 66 paragraphs in the statement. The views and opinions of the witness expressed herein do not necessarily reflect those of the Iran Human Rights Documentation Center. Page 2 of 15 Witness Statement of Karim Dahimi Statement Introduction 1. My name is Karim Dahimi. I was born in October, 1971. I was a schoolteacher and a resident of the Kuh Alavi neighborhood of Ahvaz. I am married and have three children. Initial Activities 2. My [cultural] activities began in 1989. I received my high school diploma in 1989-90 and from 1991-93, I was a university student majoring in education. Our activities at the time were limited to the distribution of statements and having connections with other groups in Mohammareh, Fallahiyeh1, Shush and other cities to hold cultural gatherings such as poetry readings. We did not engage in any other activities. Nevertheless, my file [with the security services] listed these activities as "intelligence-gathering" and "actions against national security." There was only one thing [that I did] that could have been considered very dangerous from the point of view of the Islamic Republic; my actions in relation to the sugarcane project.
    [Show full text]
  • Examining the Evolution of the Khuzestan Urban Population Using the Urban Primacy Indexes
    INTERNATIONAL JOURNAL OF SCIENTIFIC & TECHNOLOGY RESEARCH VOLUME 6, ISSUE 12, DECEMBER 2017 ISSN 2277-8616 Examining The Evolution Of The Khuzestan Urban Population Using The Urban Primacy Indexes Mokhtar Karami, Rasol Sarvestan, Ali Mohammad Mansourzadeh Abstract: Examining the status of a city in the surrounding metropolitan area network not only helpful for Specialists to understand the ups and downs of city life and surrounding it ,but also can set the groundwork for hierarchical relationships settlements and planners for discipline the urban network is studied. Research to study the evolution of the urban population in Khuzestan province was conducted during the statistical period (1957-2012). The method is a descriptive and analytical study. To collect the data, in addition the study of literature, the Facts Sheet (the statistical yearbooks and census of population and housing censuses in all courses) has been used. Then to enter data and analysis it the Excel and Minitab software was used. Models used in this study are Ginsberg index, Urban Primacy Index, Two City Index, Four City Index, Mehta’s Four City Index, Moomav and Alwosabi. The results show that is balance between the parameters of the Urban Primacy Indexes in Khuzestan province since 1957 to 1977. The process of balancing continue and is destroy until the beginning of the Imposed war and the depletion of the population of cities and in 1987 the Urban Primacy Index reached its highest level and due to the problems of the war in Ahvaz it earns the highest the Urban Primacy Index. Since 1987, the Urban Primacy Index reduced and their balancing process continues until 2012 that this balancing process due to natural population growth since after 1997.
    [Show full text]
  • Evaluation of Karun River Water Quality Scenarios Using Simulation Model Results
    Available online at http://www.ijabbr.com International journal of Advanced Biological and Biomedical Research Volume 2, Issue 2, 2014: 339-358 Evaluation of Karun River Water Quality Scenarios Using Simulation Model Results Mohammad Bagherian Marzouni a*, Ali Mohammad Akhoundalib, Hadi Moazedc, Nematollah Jaafarzadehd,e, Javad Ahadianf, Houshang Hasoonizadehg a Master Science of Civil & Environmental Eng, Faculty of Water Science Eng, Shahid Chamran University Of Ahwaz b Alimohammad Akhoondali, Professor of Water Eng, Faculty of Water Science Eng, Shahid Chamran University Of Ahwaz c Professor of Civil & Environmental Eng, Faculty of Water Science Eng, Shahid Chamran University Of Ahwaz d Environmental Technology Research Center, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran e School of Health, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran. f Assistant Professor of Water Eng, Faculty of Water Science Eng, Shahid Chamran University Of Ahwaz g Vice Basic Studies and Comprehensive Plans for Water Resources. Khuzestan Water and Power Authority. *Corresponding author: [email protected] ABSTRACT Karun River is the largest and most watery river in Iran. This river is the longest river which located just inside Iran and Ahvaz Metropolis drinking water supplied from Karun River as well (fa.alalam.ir). Karun River as the main source of water treatment plants in Ahvaz, like most surface waters affected by various contaminants which caused changes in water quality of the river (www.aww.co.ir). Causes such as constructing several dams at upstream river, withdrawal of water from the upstream to the needs of other regions of Iran, exposure of various industries along the river and discharge of industrial and urban sewage into the river, seen that today this river is deteriorating rapidly, qua today is the depth of river reach to 1 m with a high concentration of pollutants (www.tasnimnews.com).
    [Show full text]
  • How Farmers Perceive the Impact of Dust Phenomenon on Agricultural Production Activities: a Q-Methodology Study T
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Ghent University Academic Bibliography Journal of Arid Environments 173 (2020) 104028 Contents lists available at ScienceDirect Journal of Arid Environments journal homepage: www.elsevier.com/locate/jaridenv How farmers perceive the impact of dust phenomenon on agricultural production activities: A Q-methodology study T ∗ ∗∗ Fatemeh Taheria, , Masoumeh Forouzanib, , Masoud Yazdanpanahb, Abdolazim Ajilib a Department of Agricultural Economics, Ghent University, Ghent, B-9000, Belgium b Department of Agricultural Extension and Education, Agricultural Sciences and Natural Resources University of Khuzestan, Mollasani, 6341773637, Iran ARTICLE INFO ABSTRACT Keywords: Dust as one of the environmental concerns during the past decade has attracted the attention of the international Dust storms community around the world, particularly among West Asian countries. Recently, Iran has been extremely af- Farmers' perceptions fected by the serious impacts of this destructive phenomenon, especially in its agricultural sector. Management Economic and ecological impacts of dust phenomenon increasingly calls for initiatives to understand the perceptions of farmers regarding this Environmental policies phenomenon. Farmers’ views about dust phenomenon can affect their attitude and their mitigating behavior. Q method This can also make a valuable frame for decision and policy-makers to develop appropriate strategies for mi- Iran tigating dust phenomenon impacts on the agricultural sector. In line with this, a Q methodology study was undertaken to identify the perception of farmers toward dust phenomenon, in Khuzestan province, Iran. Sixty participants completed the Q sort procedure. Data analysis revealed three types of perceptions toward dust phenomenon: health adherents who seek support, government blamers who seek support, and planning ad- herents who seek information.
    [Show full text]
  • Of Khuzestan Province, Southwestern Iran
    Archive of SID Persian J. Acarol., 2018, Vol. 7, No. 4, pp. 323–344. http://dx.doi.org/10.22073/pja.v7i4.38663 Journal homepage: http://www.biotaxa.org/pja Article Some mesostigmatic mites (Acari: Parasitiformes) of Khuzestan province, southwestern Iran Sara Farahi1, Parviz Shishehbor1 and Alireza Nemati2 1. Department of Plant Protection, Faculty of Agriculture, Shahid Chamran University of Ahvaz, Ahvaz, Iran; E-mails: [email protected], [email protected] 2. Department of Plant Protection, Faculty of Agriculture, Shahrekord University, Shahrekord, Iran; E-mail: [email protected] ABSTRACT Animal droppings constitute an ephemeral habitat where specialized invertebrate communities including significant abundance of mites live together. In order to study the Mesostigmata mites associated with manure, samples were taken from different manure types of domestic animals and poultry in Ahvaz and its vicinity in Khuzestan Province, southwestern of Iran, over a period of two years (2015-2017). Here we report 20 species belonging to eight families of Mesostigmata, among which 14 species are new records for the fauna of Khuzestan Province. The genus and species Leitneria pugio (Karg, 1961) is newly recorded from Iran. The genus and species were previously only recorded in Europe. Also, Uroobovella varians Hirschmann & Zirngiebl-Nicol, 1962 is recorded for the first time from Iran based on deutonymph stage. We further provide collection data for each species along with a key for known Iranian species of the genus Uroobovella. KEY WORDS: Mesostigmata; Manure-inhabiting mites; Uroobovella; Ahvaz; Iran. PAPER INFO.: Received: 9 May 2018, Accepted: 10 August 2018, Published: 15 October 2018 INTRODUCTION Animal manures possess a rich fauna of arthropods including significant abundance of mites.
    [Show full text]
  • See the Document
    IN THE NAME OF GOD IRAN NAMA RAILWAY TOURISM GUIDE OF IRAN List of Content Preamble ....................................................................... 6 History ............................................................................. 7 Tehran Station ................................................................ 8 Tehran - Mashhad Route .............................................. 12 IRAN NRAILWAYAMA TOURISM GUIDE OF IRAN Tehran - Jolfa Route ..................................................... 32 Collection and Edition: Public Relations (RAI) Tourism Content Collection: Abdollah Abbaszadeh Design and Graphics: Reza Hozzar Moghaddam Photos: Siamak Iman Pour, Benyamin Tehran - Bandarabbas Route 48 Khodadadi, Hatef Homaei, Saeed Mahmoodi Aznaveh, javad Najaf ...................................... Alizadeh, Caspian Makak, Ocean Zakarian, Davood Vakilzadeh, Arash Simaei, Abbas Jafari, Mohammadreza Baharnaz, Homayoun Amir yeganeh, Kianush Jafari Producer: Public Relations (RAI) Tehran - Goragn Route 64 Translation: Seyed Ebrahim Fazli Zenooz - ................................................ International Affairs Bureau (RAI) Address: Public Relations, Central Building of Railways, Africa Blvd., Argentina Sq., Tehran- Iran. www.rai.ir Tehran - Shiraz Route................................................... 80 First Edition January 2016 All rights reserved. Tehran - Khorramshahr Route .................................... 96 Tehran - Kerman Route .............................................114 Islamic Republic of Iran The Railways
    [Show full text]
  • Novel Hydraulic Structures and Water Management in Iran: a Historical Perspective
    Novel hydraulic structures and water management in Iran: A historical perspective Shahram Khora Sanizadeh Department of Water Resources Research, Water Research Institute������, Iran Summary. Iran is located in an arid, semi-arid region. Due to the unfavorable distribution of surface water, to fulfill water demands and fluctuation of yearly seasonal streams, Iranian people have tried to provide a better condition for utilization of water as a vital matter. This paper intends to acquaint the readers with some of the famous Iranian historical water monuments. Keywords. Historic – Water – Monuments – Iran – Qanat – Ab anbar – Dam. Structures hydrauliques et gestion de l’eau en Iran : une perspective historique Résumé. L’Iran est situé dans une région aride, semi-aride. La répartition défavorable des eaux de surface a conduit la population iranienne à créer de meilleures conditions d’utilisation d’une ressource aussi vitale que l’eau pour faire face à la demande et aux fluctuations des débits saisonniers annuels. Ce travail vise à faire connaître certains des monuments hydrauliques historiques parmi les plus fameux de l’Iran. Mots-clés. Historique – Eau – Monuments – Iran – Qanat – Ab anbar – Barrage. I - Introduction Iran is located in an arid, semi-arid region. Due to the unfavorable distribution of surface water, to fulfill water demands and fluctuation of yearly seasonal streams, Iranian people have tried to provide a better condition for utilization of water as a vital matter. Iran is located in the south of Asia between 44º 02´ and 63º 20´ eastern longitude and 25º 03´ to 39º 46´ northern latitude. The country covers an area of about 1.648 million km2.
    [Show full text]
  • An Investigation on the Systems of Collecting and Extracting Greywater from Surface Water and Wastewater
    American Journal of Engineering and Applied Sciences Original Research Paper An Investigation on the Systems of Collecting and Extracting Greywater from Surface Water and Wastewater 1 2 3 4 Saeid Eslamian, Mohammad Abdolhoseini, Kaveh Ostad-Ali-Askari and Vijay P. Singh 1Department of Water Engineering, College of Agriculture, Isfahan University of Technology, Isfahan, 8415683111, Iran 2Department of Water Engineering, Gorgan University of Agricultural Sciences and Natural Resources, Gorgan, Iran 3Department of Water Engineering, College of Agriculture, Isfahan University of Technology, Isfahan, 8415683111, Iran 4Department of Biological and Agricultural Engineering and Zachry Department of Civil Engineering, Texas A and M University, 321 Scoates Hall, 2117 TAMU, College Station, Texas 77843-2117, USA Article history Abstract: Lack of water resources, on the one hand and degradation of Received: 19-05-2018 the quality of available resources; on the other hand, raise serious Revised: 07-07-2018 concerns about water supply. Limited water resources in some areas Accepted: 15-08-2018 necessitate planning for use of unconventional resources, such as: Corresponding Author: Unconventional and recyclable water resources, which should be used Mohammad Abdolhoseini optimally. Therefore, there is an increasing need for use of low-quality Department of Water water in areas where freshwater is scarce, in which case, Engineering, Gorgan University unconventional water resources (such as saline water, brackish water of Agricultural Sciences and and household wastewater) can be considered as valuable resources. Natural Resources, Gorgan, Iran The aim of this study was to investigate the possibility of water Email: extraction from household wastewater (greywater) and surface water mohammad.abdolhoseini24@g mail.com running in villages in Abadan and to simultaneously evaluate some water collection systems to find the best one in order to use these water resources as unconventional and recyclable water resources for various uses such as: Agriculture and irrigation of date palms.
    [Show full text]
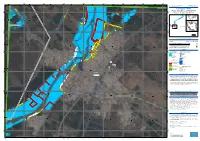
  • HAMIDIYEH, V1 Hamidiyeh - IRAN 0 0 0 0
    254500 255000 255500 256000 256500 257000 257500 258000 48°24'40"E 48°25'0"E 48°25'20"E 48°25'40"E 48°26'0"E 48°26'20"E 48°26'40"E 48°27'0"E GLIDE number: FL-2019-000022-IRN Activation ID: EMSR352 Int. Charter call ID: 601 Product N.: 06HAMIDIYEH, v1 Hamidiyeh - IRAN 0 0 0 0 5 5 Flood - Situation as of 08/04/2019 7 7 8 8 4 4 3 3 Grading - Ready-to-print Map 01 N " 0 h 4 e ' h 9 rk 2 a ° K 1 3 Azerbaijan Turkmenistan Caspian N " 0 Sea 4 ' 9 2 ° 1 Tehran 3 ^ Dasht-e-Azadegan Hamidiyeh (! Khuzestan Iran Iraq RTP01 06 Kuwait Saudi Persian 0 0 Arabia Qatar 0 0 Gulf Gulf of Oman 0 0 7 7 8 8 4 4 3 3 6 km Cartographic Information 1:6000 Full color A1, 200 dpi resolution N " 0 2 ' 0 0,125 0,25 0,5 9 2 ° km 1 3 Grid: WGS 1984 UTM Zone 39N map coordinate system N " 0 2 ' Tick marks: WGS 84 geographical coordinate system 9 2 ± ° 1 3 Legend 0 0 0 0 5 5 6 6 8 8 Crisis Information Administrative boundaries 4 4 3 3 Flooded Area (08/04/2019 07:38 UTC) Province Flood trace Placenames ! Built Up Grading Placename Destroyed Hydrography Stream Damaged Reservoir Possibly damaged Transportation Grading River Road, Destroyed Stream Road, Damaged Transportation Bridge and elevated highway Road, Possibly damaged N " Primary Road 0 ' General Information 9 2 ° 1 3 Area of Interest Local Road 0 0 0 0 0 0 Cart Track N 6 6 " 8 8 0 ' 4 4 Ahvaz 9 2 3 3 ° 1 3 Map Information Hamidiyeh ! Severe flooding in several provinces of Iran since mid-March, has left 70 people dead.
    [Show full text]