Optimal Non-Linear Income Tax When Highly Skilled Individuals Vote with Their Feet
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

SP Manweb Use of System Charging Statement NOTICE of CHARGES Effective from 1St April 2020 Version
SP Manweb Use of System Charging Statement NOTICE OF CHARGES Effective from 1st April 2020 Version 0.1 This statement is in a form to be approved by the Gas and Electricity Markets Authority. 3 PRENTON WAY, BIRKENHEAD, MERSEYSIDE CH43 3ET 02366937 SP MANWEB PLC DECEMBER 2018 V0.1 Version Control Version Date Description of version and any changes made A change-marked version of this statement can be provided upon request. 3 PRENTON WAY, BIRKENHEAD, MERSEYSIDE CH43 3ET 02366937 SP MANWEB PLC DECEMBER 2018 V0.1 Contents 1. Introduction 5 Validity period 6 Contact details 6 1.14. For all other queries please contact our general enquiries telephone number: 0330 10 10 4444 7 2. Charge application and definitions 8 The supercustomer and site-specific billing approaches 8 Supercustomer billing and payment 9 Site-specific billing and payment 10 Incorrectly allocated charges 16 Generation charges for pre-2005 designated EHV properties 17 Provision of billing data 18 Out of area use of system charges 18 Licensed distribution network operator charges 18 Licence exempt distribution networks 19 3. Schedule of charges for use of the distribution system 21 4. Schedule of line loss factors 22 Role of line loss factors in the supply of electricity 22 Calculation of line loss factors 22 Publication of line loss factors 23 5. Notes for Designated EHV Properties 24 EDCM network group costs 24 Charges for new Designated EHV Properties 24 Charges for amended Designated EHV Properties 24 Demand-side management 24 6. Electricity distribution rebates 26 7. Accounting and administration services 26 8. -

SP Manweb Use of System Charging Statement NOTICE of CHARGES
SP Manweb Use of System Charging Statement NOTICE OF CHARGES Effective from 1st April 2021 Version 0.1 This statement is in a form to be approved by the Gas and Electricity Markets Authority. 3 PRENTON WAY, BIRKENHEAD, MERSEYSIDE CH43 3ET 02366937 SP MANWEB PLC DECEMBER 2019 V0.1 Version Control Version Date Description of version and any changes made A change-marked version of this statement can be provided upon request. 3 PRENTON WAY, BIRKENHEAD, MERSEYSIDE CH43 3ET 02366937 SP MANWEB PLC DECEMBER 2019 V0.1 Contents 1. Introduction 5 Validity period 6 Contact details 6 2. Charge application and definitions 8 The supercustomer and site-specific billing approaches 8 Supercustomer billing and payment 9 Site-specific billing and payment 10 Incorrectly allocated charges 15 Generation charges for pre-2005 designated EHV properties 16 Provision of billing data 17 Out of area use of system charges 17 Licensed distribution network operator charges 18 Licence exempt distribution networks 18 3. Schedule of charges for use of the distribution system 20 4. Schedule of line loss factors 21 Role of line loss factors in the supply of electricity 21 Calculation of line loss factors 21 Publication of line loss factors 22 5. Notes for Designated EHV Properties 23 EDCM network group costs 23 Charges for new Designated EHV Properties 23 Charges for amended Designated EHV Properties 23 Demand-side management 23 6. Electricity distribution rebates 25 7. Accounting and administration services 25 8. Charges for electrical plant provided ancillary to the grant -

Renewable Energy Route Map for Wales Consultation on Way Forward to a Leaner, Greener and Cleaner Wales Renewable Energy Route Map for Wales 3
Renewable Energy Route Map for Wales consultation on way forward to a leaner, greener and cleaner Wales Renewable Energy Route Map for Wales 3 Contents Minister’s foreword Introduction 1 Purpose of consultation 2 Setting the scene Part one: Wales renewable energy resources 3 Biomass 4 Marine: tides and waves 5 Hydro-electricity 6 Waste 7 Wind: on-shore and off-shore Part two: energy conservation and distributed renewable generation objectives 8 Energy efficiency /micro-generation 9 Large-scale distributed generation(‘off-grid’) Part three: context 10 Consenting regimes 11 Grid Infrastructure developments 12 Research and development Part four: invitation to respond 13 Opportunities and contact details Part five: Summary of route map commitments Annex A: Summary of possible electricity and heat generation from renewable energy in Wales by 2025 Annex B: Existing Welsh Assembly Government targets and commitments Annex C: Indicative data on Wales’ energy demand, supply and greenhouse emissions Annex D: Future costs of renewable energy/banding of the Renewables Obligation Annex E: Data base of potential large on-shore wind power schemes in Wales Annex F: Availability of potential waste derived fuels Annex G: UK/Wales energy consumption breakdowns Annex H: Major energy developments since July 2007 © Crown Copyright 2008 CMK-22-**-*** G/596/07-08 Renewable Energy Route Map for Wales Renewable Energy Route Map for Wales 5 Ministerial Foreword We now need to look radically at the options and resources available to us and collaborate with the key energy and building sectors to support fundamental change within “The time for equivocation is over. The science is clear. -

Duos Contract Managers
Distribution Use of System Contract Managers East Midlands: [email protected] John Hill Central Networks (East) plc Herald Way Pegasus Business Park East Midlands Airport Castle Donington DE74 2TU Tel: 01332 393322 Fax: 01332 393021 Eastern & London: [email protected] Peter Waymont DUOS Contracts Manager EDF Energy Networks (EPN) plc & EDF Energy Networks (LPN) plc Atlantic House Henson Road Three Bridges Crawley RH10 1QQ Tel: 01293 509324 Fax: 01293 577731 Midlands: [email protected] John Hill Central Networks (West) plc Herald Way Pegasus Business Park East Midlands Airport Castle Donington DE74 2TU Tel: 01332 393322 Fax: 01332 393021 Northern: [to be confirmed] Joseph Hart Strategy Manager or Jamie Law DUOS Contracts manager Norweb: [email protected] Tony Savka Use of System Contract Manager United Utilities Electricity plc Dawson House Greak Sankey Warrington WA5 3LW Tel: 01772 848680 Fax: 01772 848670 Scottish Hydro [email protected] & Southern: Craig Neill Power Systems Contracts Manager Scottish and Southern Energy plc Inveralmond House 200 Dunkeld Road Perth PH1 3AQ Tel: 01738 456463 Fax: 01738456555 Manweb & Scottish Power: [email protected] Doug Houlbrook SP MANWEB plc Trading Services Group SP Power Systems Prenton Way Birkenhead Merseyside L43 3ET Tel: 0151 609 2022 Fax: Seeboard: [email protected] Peter Waymont DUOS Contracts Manager EDF Energy Networks (SPN) plc Atlantic House Henson Road Three Bridges Crawley West Sussex RH10 1QQ Tel: 01293 509324 Fax: 01293 577731 South Wales : [email protected] Karl Williams Use of Systems Contracts Manager Lamby Way Industrial Estate Lamby Way, Rumney, Cardiff CF3 8EH Tel: 02920 535118 Fax: 02920 535150 Western Power: [email protected] Andy Hood DUOS Contracts Manager Western Power Distribution (South West) plc Avonbank Feeder Road Bristol BS2 0TB Tel: 0117 933 2438 Fax: 0117 933 2007 Yorkshire: [to be confirmed] Joseph Hart Strategy Manager or Jamie Law DUOS Contracts Manager . -
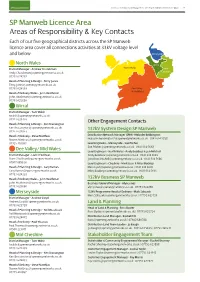
SP Manweb Licence Area Areas of Responsibility & Key Contacts SP Distri Areas Of
19 SP Energy Networks Incentive on Connections Engagement (ICE) Ofgem Submission October Update 20 SP Manweb Licence Area SP Distribution Licence Area This Area of Responsibility List was created as a direct result of our stakeholders Areas of Responsibility & Key Contacts Areas of Responsibility & Key Contacts requesting information and access to our key contacts Each of our five geographical districts across the SP Manweb in our Districts and has been Each of our six geographical districts across the SP Distribution licence area cover all connections activities at 33kV voltage level warmly welcomed. licence area cover all connections activities at 33kV voltage level and below Merseyside and below North Wales Wirral District Manager - Andrew Churchman North Wales Mid Edinburgh & Borders [email protected] Cheshire Glasgow District General Manager - Ian Johnston 07753 624757 Central [email protected] | 07753 624803 & Fife Head of Planning & Design - Terry Jones Head of Planning & Design - Gordon Burrows [email protected] Lanarkshire [email protected] | 07725 410347 Edinburgh 07753 624359 Dee Valley & Borders & Mid Wales Head of Delivery - Mark Everett Head of Delivery Wales - John Heathman [email protected] | 07753 624104 Ayrshire & [email protected] Clyde South 07753 623886 Head of Delivery - Sean Gavaghan [email protected] | 07789 925327 Wirral Dumfries Central & Fife District Manager - Tom Walsh [email protected] -
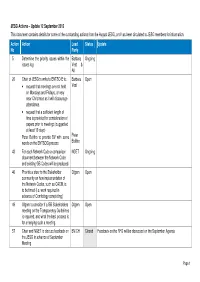
JESG Actions
JESG Actions – Update 12 September 2012 This document contains details for some of the outstanding actions from the August JESG, and has been circulated to JESG members for information. Action Action Lead Status Update No Party 5 Determine the priority issues within the Barbara Ongoing issues log Vest & All 20 Chair of JESG to write to ENTSO-E to: Barbara Open • request that meetings are not held Vest on Mondays and Fridays, or very near Christmas as it will discourage attendance. • request that a sufficient length of time is provided for consideration of papers prior to meetings (suggested at least 10 days) Peter Bolitho to provide BV with some Peter words on the ENTSOG process Bolitho 42 For each Network Code a comparison NGET Ongoing document between the Network Code and existing GB Codes will be produced. 46 Provide a steer to the Stakeholder Ofgem Open community on how implementation of the Network Codes, such as CACM, is to be timed (i.e. work required in advance of Comitology completing) 49 Ofgem to consider if a GB Stakeholders Ofgem Open meeting on the Transparency Guidelines is required, and what the best process is for arranging such a meeting. 57 Chair and NGET to discuss feedback on BV/CH Closed Feedback on the RFG will be discussed on the September Agenda the JESG in advance of September Meeting Page 1 Action Action Lead Status Update No Party 58 Chair and NGET to discuss and agree BV/PW Closed New Dates circulated dates for JESG meetings in 2013 59 Feedback/Queries to ENTSO-E: NGET Closed 1. -

7.3 Strategic Options Report
The North Wales Wind Farms Connection Project Strategic Options Report Application reference: EN020014 March 2015 Regulation reference: The Infrastructure Planning (Applications: Prescribed Forms and Procedure) Regulations 2009 Regulation 5(2)(q) Document reference 7.3 The Planning Act 2008 The Infrastructure Planning (Applications: Prescribed Forms and Procedure) Regulations 2009 Regulation 5(2)(q) The North Wales Wind Farms Connection Project Strategic Options Report Document Reference No. 7.3 Regulation No. Regulation 5(2)(q) Author SP Manweb Date March 2015 Version V1 Planning Inspectorate Reference EN020014 No. SP Manweb plc, Registered Office: 3 Prenton Way Prenton CH43 3ET. Registered in England No. 02366937 SUMMARY The North Wales Wind Farms Connection Project is a major electrical infrastructure development project, involving several wind farm developers and the local Distribution Network Operator – SP Manweb plc (SP Manweb). The development of on-shore wind generation in Wales is guided by the Welsh Government’s energy strategy, initially published in 2003. In their Technical Advice Note (TAN) 8: renewable energy (2005) the Welsh Government identified 7 Strategic Search Areas (SSAs) as potential locations for wind generation, of which area A is in North Wales. During the past 20 years, approximately 220 MW of wind generation (both onshore and offshore) have been connected to the SP Manweb distribution network in North Wales. Within the TAN 8 SSA A, SP Manweb is currently contracted to connect a further four wind farms[1] which have received planning consent and total 170 MW of generation. SP Manweb has a statutory duty to offer terms to connect new generating stations to its distribution system. -

The Net Zero North West Cluster Plan Phase 1: Shaping an Industrial Cluster Plan
The Net Zero North West Cluster Plan Phase 1: Shaping an Industrial Cluster Plan FINAL REPORT AUGUST 2020 PROJECT PARTNERS: Net Zero North West Cluster Plan Phase 1 : Shaping an Industrial Cluster Plan Contents Page Foreword 3 Executive Summary 4 Phase 1 Programme Activity 5 Phase 2 Programme Design 7 1. Introduction 9 Phase 1 Project Partners 10 2. Decarbonising Industrial Production in the North West 11 Why is it important to decarbonise industry? 11 Regional & Sub-regional drivers 14 3. Net Zero NW Cluster Plan – Phase 1 23 Industry Engagement 24 Phase 1 Research 25 4. Phase 1 Business Case Recommendations Summary 32 5. Net Zero NW Cluster Plan – Phase 2 36 Phase 2 – Additional Project Partners 38 Industry and Local Government Collaboration 39 A. Industrial Consumers Workstream 43 B. Networks Workstream 44 C. Generation & Production Workstream 45 An Industrial Cluster Plan 46 APPENDIX A - PHASE 2 WORKSTREAMS ANNEXES ANNEX A – EXISTING ASSETS, EMISSIONS DATA ANNEX B – INDUSTRIAL ZONES ANNEX C – SOCIO-ECONOMIC IMPACTS Net Zero North West Cluster Plan Phase 1 : Shaping an Industrial Cluster Plan Foreword “Home to the industrial revolution, the North West is still a powerhouse of manufacturing and chemical production. Decarbonising our industry is not only vital to the UK’s net zero ambitions but is critical to safeguard and grow the high value jobs that make this region thrive. “Led by industry, Net Zero North West is driving investment into the net zero economy and post COVID-19 green recovery in the North West. Our strength lies in the unrivalled number of initiatives already happening on the ground which offer sustainable investment opportunities in net zero and will see this region become a world leader in clean growth. -

UK Offshore Wind Power Market Update Overview of the UK Offshore Wind Power Market and Points to Note for New Entrants May 2019
UK Offshore Wind Power Market Update Overview of the UK offshore wind power market and points to note for new entrants May 2019 英国海上风电市场投资指南 | 经济及金融形势概览 02 2018年大型上市银行 | 引言 Contents Executive Summary 1 Chapter 1 UK Power Market Overview 3 1.1 Market structure 3 1.2 Market Status 7 1.3 Power Trading 9 1.4 European Commission power market legislation 11 Chapter 2 UK Offshore Wind Market 12 2.1 Market overview 12 2.2 Statutory stakeholders in UK offshore wind market 17 2.3 The Offshore Wind Sector Deal 19 Chapter 3 Project Development Key Steps 22 3.1 Project lifecycle 22 3.2 Seabed Leasing 23 3.3 Planning Consent and generation licence 29 3.4 Contract for Difference (CfD) auction 31 3.5 Transfer offshore transmission asset 41 Summary 48 Contact Details 50 1 英国海上风电市场投资指南 | 经济及金融形势概览 1 UK Offshore Wind Power Market Update | Executive Summary Executive Summary UK power market is one of the most liberalised power market in the world with sophisticated regulatory schemes to support efficiency and encourage competition. The openness and transparency of the UK power market have made it one of the most attractive destinations for overseas investors including strategic investors such as major utilities as well as infrastructure funds and other financial investors. Similar to many other markets in the world, the UK power market is going through a transition towards a cleaner energy mix. The UK will phase out coal-fired power plant by 2025 and offshore wind power is playing an increasingly important role in delivering the low carbon energy mix. -

Articles Case
CONTENTS : ELM 15[2003]6 341 Volume 15 Issue 6 2003 ISSN 1067 6058 Editorial NIMBY-ism and the spectre of maritime pollution 343 DAVID POCKLINGTON Articles PROFESSOR D E FISHER The principles of a contemporary environmental legal system 347 Queensland University of Technology CLAIRE HOWELL The environmental dimension to company law modernisation 354 DR BEN PONTIN University of the West of England, Bristol Case commentary Rylands v Fletcher restated – the House of Lords’ decision in 367 JASON LOWTHER Transco plc v Stockport Metropolitan Borough Council University of Wolverhampton Case Law EC LAW Ligue pour la protection des oiseaux and others v Premier Ministre, Ministre de 370 l’Amenagement – preliminary ruling on hunting seasons Criminal Proceedings concerning Nilsson – interpretation of trade in endangered 371 species regulations CIVIL LIABILITY Loftus-Brigham and another v Ealing London Borough Council – tree roots and 372 causation issues Daiichi UK Ltd v Stop Huntingdon Animal Cruelty – corporations and the tort of 373 harassment PLANNING LAW R (Jones) v Mansfield District Council – planning and EIA 374 Evans v First Secretary of State – screening directions in EIA 375 WILDLIFE Hughes v DPP – possession of wild birds 377 Case round-up Packaging offences – waste management – water pollution – PPC 378 Strategic Issues Biofuels EFRA, Seventeenth Report, Session 2002–2003 (HC 929) 383 World Summit on Sustainable Development 2002 – From Rhetoric to Reality EAC, Twelve Report, Session 2002–2003 (HC 98) Government’s Response to EAC Tenth -

SP MANWEB PLC Use of System Charging
SP MANWEB PLC Use of System Charging Statement NOTICE OF CHARGES Effective from 1st April 2018 Version 1.1 This statement is in a form to be approved by the Gas and Electricity Markets Authority. 3 PRENTON WAY, BIRKENHEAD, MERSEYSIDE CH43 3ET 02366937 SP MANWEB PLC DECEMBER 2016 Version Control Version Date Description of version and any changes made V1.1 8/2/18 Annex 5 updated with 2018/19 LAFs V1.1 8/2/18 Supplier of Last Resort increases to the Fixed Charges for the Domestic Unrestricted, Domestic Two Rate and LV Domestic Network tariffs (Annex 1). The increase for each of these tariffs is 0.08p/MPAN/day. No other tariffs affected by this change. A change-marked version of this statement can be provided upon request. PRENTON WAY, BIRKENHEAD, MERSEYSIDE, CH43 3ET SP MANWEB PLC DECEMBER 2016 Contents 1. Introduction 4 Validity period 5 Contact details 5 2. Charge application and definitions 6 Supercustomer billing and payment 6 Site-specific billing and payment 8 Application of charges for excess reactive power 12 Incorrectly allocated charges 14 Generation charges for pre-2005 designated EHV properties 15 Provision of billing data 16 Out of area use of system charges 16 Licensed distribution network operator charges 17 Licence exempt distribution networks 17 3. Schedule of charges for use of the distribution system 20 4. Schedule of line loss factors 21 Role of line loss factors in the supply of electricity 21 Calculation of line loss factors 21 Publication of line loss factors 22 5. Notes for Designated EHV Properties 23 EDCM network group costs 23 Charges for new Designated EHV Properties 23 Charges for amended Designated EHV Properties 23 Demand-side management 23 6. -

AC Line, Connah's Quay to Dolgarrog
CPAT Report No. 1628 AC Line, Connah’s Quay to Dolgarrog Desk-based Assessment YMDDIRIEDOLAETH ARCHAEOLEGOL CLWYD-POWYS CLWYD-POWYS ARCHAEOLOGICAL TRUST Client name: SP Manweb PLC / SP Energy Networks CPAT Project No: 2339 Project Name: AC Line Grid Reference: SJ 2711 7141 to SH 7702 6776 County/LPA: Flintshire, Denbighshire and Conwy CPAT Report No: 1628 Report status: Final Confidential until: 31 December 2019 Prepared by: Checked by: Approved by: Nigel Jones Paul Belford Paul Belford Principal Archaeologist Director Director 12 December 2018 13 December 2018 14 December 2018 Bibliographic reference: Jones, N. W., 2018. AC Line, Connah’s Quay to Dolgarrog: Desk-based Assessment. Unpublished report. CPAT Report No. 1628. YMDDIRIEDOLAETH ARCHAEOLEGOL CLWYD-POWYS CLWYD-POWYS ARCHAEOLOGICAL TRUST 41 Broad Street, Welshpool, Powys, SY21 7RR, United Kingdom +44 (0) 1938 553 670 [email protected] www.cpat.org.uk ©CPAT 2018 The Clwyd-Powys Archaeological Trust is a Registered Organisation with the Chartered Institute for Archaeologists CONTENTS SUMMARY ................................................................................................................................................... II 1 INTRODUCTION ................................................................................................................................. 1 2 NATURE OF THE SCHEME ................................................................................................................... 1 3 METHODOLOGY ...............................................................................................................................