DOCSLIB.ORG

Surveys, Collections, Handbooks, Etc

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Surveys, Collections, Handbooks, Etc Graph Layout Support for Model-Driven Engineering Dipl.-Inf. Miro Spönemann Dissertation zur Erlangung des akademischen Grades Doktor der Ingenieurwissenschaften (Dr.-Ing.) der Technischen Fakultät der Christian-Albrechts-Universität zu Kiel eingereicht im Jahr 2014 Kiel Computer Science Series (KCSS) 2015/2 v1.0 dated 2015-3-13 ISSN 2193-6781 (print version) ISSN 2194-6639 (electronic version) Electronic version, updates, errata available via https://www.informatik.uni-kiel.de/kcss Published by the Department of Computer Science, Kiel University Real-Time and Embedded Systems Group Please cite as: Ź Miro Spönemann. Graph layout support for model-driven engineering. Number 2015/2 in Kiel Computer Science Series. Dissertation, Faculty of Engineering, Christian-Albrechts- Universität zu Kiel, 2015. @book{Spoenemann15, author = {Miro Sp{\"o}nemann}, title = {Graph layout support for model-driven engineering}, publisher = {Department of Computer Science}, year = {2015}, isbn = {9783734772689}, series = {Kiel Computer Science Series}, number = {2015/2}, note = {Dissertation, Faculty of Engineering, Christian-Albrechts-Universit\"at zu Kiel} } © 2015 by Miro Spönemann Herstellung und Verlag: BoD – Books on Demand, Norderstedt ISBN 978-3-7347-7268-9 ii About this Series The Kiel Computer Science Series (KCSS) covers dissertations, habilitation theses, lecture notes, textbooks, surveys, collections, handbooks, etc. written at the Department of Computer Science at Kiel University. It was initiated in 2011 to support authors in the dissemination of their work in electronic and printed form, without restricting their rights to their work. The series provides a unified appearance and aims at high-quality typography. The KCSS is an open access series; all series titles are electronically available free of charge at the department’s website. In addition, authors are encouraged to make printed copies available at a reasonable price, typically with a print-on-demand service. Please visit http://www.informatik.uni-kiel.de/kcss for more information, for instructions how to publish in the KCSS, and for access to all existing publications. iii 1. Gutachter: Prof. Dr. Reinhard von Hanxleden Institut für Informatik Christian-Albrechts-Universität zu Kiel 2. Gutachter: Prof. Dr. Petra Mutzel Fakultät für Informatik Technische Universität Dortmund 3. Gutachter: Prof. Dr. Wilhelm Hasselbring Institut für Informatik Christian-Albrechts-Universität zu Kiel Datum der mündlichen Prüfung: 9. Februar 2015 iv Zusammenfassung Wie bereits von Fuhrmann gezeigt [Fuh11], kann die Produktivität modell- getriebener Softwareentwicklung durch zahlreiche Konzepte zur Verbesse- rung der praktischen Handhabung von Modellen erhöht werden. Dabei ist das automatische Layout graphenbasierter Modelle ein zentraler Schlüssel. Allerdings gibt es einen bemerkenswerten Kontrast zwischen der Fülle an Forschungsergebnissen im Bereich des Graphen-Layout und dem aktuellen Stand graphischer Modellierungswerkzeuge, bei denen nur ein kleiner Teil dieser Ergebnisse übernommen wird. Das Ziel dieser Arbeit ist diese Lücke auf drei separaten Ebenen zu überbrücken: spezialisierte Layout-Algorith- men, Verwaltung von Konfigurationen und Software-Infrastruktur. Im Bezug auf Layout-Algorithmen liegt der Schwerpunkt auf dem Layer- basierten Ansatz. Wir untersuchen dessen Erweiterung zur Unterstützung von Ports und Hyperkanten, was wesentliche Bestandteile bestimmter Ar- ten von Graphen sind, z. B. Datenflussmodelle. Der Hauptbeitrag ist die Einbeziehung von Bedingungen für die Positionierung von Ports, vor al- lem während der Kreuzungsminimierung und der Kantenführungsphase. Hyperkanten werden durch normale Kanten repräsentiert, was deren Verar- beitung vereinfacht aber Ungenauigkeiten beim Zählen von Kreuzungen verursacht. Als letzte Erweiterung betrachten wir einen Sketch-basierten Ansatz für die einfache Integration von Nutzerinteraktivität. Ein abstraktes Layout ist die Auswahl eines Layout-Algorithmus zusam- men mit einer Abbildung seiner Parameter auf konkrete Werte, während ein konkretes Layout Positionsdaten beschreibt, die von einem Algorithmus berechnet wurden. Wir diskutieren ein neues Metamodell, mit dem sowohl die Struktur als auch das abstrakte sowie das konkrete Layout eines Gra- phen spezifiziert werden kann. Dies bildet eine Grundlage für die effiziente Verwaltung von Layout-Konfigurationen. Zudem untersuchen wir einen evolutionären Algorithmus für die Suche im Lösungsraum abstrakter Lay- outs, wobei zur Bewertung von Lösungen Ästhetikkriterien ausgewertet werden. v Die in dieser Arbeit entwickelte Software-Infrastruktur hat als Ziel, beliebige Graphen-basierte Diagramme (front-ends) mit beliebigen Layout- Algorithmen (back-ends) zu verbinden. Die größte Herausforderung dabei ist das Finden geeigneter Abstraktionen, die eine solche Allgemeingültigkeit erlauben und gleichzeitig die Komplexität so niedrig wie möglich halten. Wir betrachten eine mögliche Realisierung, die auf Eclipse basiert, eine von vielen Modellierungswerkzeugen verwendete Plattform. Eine Web-basierte Umfrage wurde unter Nutzern der Layout-Infrastruktur durchgeführt, um zu untersuchen inwieweit die gesteckten Ziele erfüllt worden sind. Die allgemeine Resonanz zu dieser Umfrage ist sehr positiv. vi Abstract As shown previously by Fuhrmann [Fuh11], there are several concepts for increasing the productivity of model-driven engineering by improving the practical handling of models. The automatic layout of graph-based models is a key enabler in this context. However, there is a striking contrast between the abundance of research results in the field of graph layout methods and the current state of graphical modeling tools, where only a tiny fraction of these results are ever adopted. This thesis aims to bridge this gap on three separate levels: specialized layout algorithms, configuration management, and software infrastructure. Regarding layout algorithms, here we focus on the layer-based approach. We examine its extension to include ports and hyperedges, which are essential features of certain kinds of graphs, e. g. data flow models. The main contribution is the handling of constraints on the positioning of ports, which is done mainly in the crossing minimization and edge routing phases. Hyperedges are represented with normal edges, simplifying their handling but introducing inaccuracies for counting crossings. A final extension discussed here is a sketch-driven approach for simple integration of user interactivity. An abstract layout is the selection of a layout algorithm with a mapping of its parameters to specific values. We discuss a new meta model allowing to specify the structure of a graph as well as its abstract layout and its concrete layout, i. e. positioning data computed by the layout algorithm. This forms a basis for efficient management of layout configurations. Furthermore, we investigate an evolutionary algorithm for searching the solution space of abstract layouts, taking readability criteria into account for evaluating solutions. The software infrastructure developed here targets the connection of arbitrary diagram viewers (front-ends) with arbitrary graph layout algo- rithms (back-ends). The main challenge is to find suitable abstractions that vii allow such generality and at the same time keep the complexity as low as possible. We discuss a possible realization based on the Eclipse plat- form, which is used by several modeling tools, e. g. the Graphical Modeling Framework (GMF). A web-based survey has been conducted among users of the layout infrastructure in order to evaluate to what extent the stated goals have been met. The overall feedback collected from this survey is very positive. viii Contents 1 Introduction1 1.1 Contributions of This Thesis....................4 1.1.1 Publications.........................6 1.2 Modeling Languages........................ 11 1.2.1 Data Flow Languages................... 12 1.2.2 Control Flow Languages.................. 12 1.2.3 Static Structure Languages................ 15 1.3 Definitions.............................. 16 1.3.1 Graphs............................ 16 1.3.2 Graph Layout........................ 18 1.3.3 Statistics........................... 19 1.4 Graph Layout Methods....................... 22 1.4.1 Planarization-Based Layout................ 22 1.4.2 Force-Based Layout..................... 27 1.4.3 Tree and Circular Layout................. 28 1.5 The KIELER Project......................... 29 1.6 Related Work............................ 30 I Layout Algorithms 37 2 The Layer-Based Approach 39 2.1 Base Algorithms........................... 40 2.1.1 Elimination of Cycles................... 40 2.1.2 Layer Assignment..................... 41 2.1.3 Crossing Minimization................... 44 2.1.4 Node Placement...................... 46 2.1.5 Edge Routing........................ 47 2.2 Port Constraints........................... 48 2.2.1 Handling Constraint Levels................ 49 2.2.2 Crossing Minimization................... 52 ix Contents 2.2.3 Edge Routing........................ 59 2.2.4 Evaluation.......................... 66 2.3 Hyperedges............................. 75 2.3.1 General Representation.................. 75 2.3.2 Junction Points....................... 79 2.3.3 Counting Crossings.................... 81 2.3.4 Evaluation.......................... 87 2.4 Interactive Layout.......................... 92 2.4.1 Layer-Based Sketch-Driven Layout............ 93 2.4.2 Evaluation.......................... 97 3 Meta Layout 103 3.1 A Generic Layout Interface...................
Load more

Recommended publications
  • Textual, Executable, Translatable UML⋆
    Textual, executable, translatable UML? Gergely D´evai, G´abor Ferenc Kov´acs, and Ad´amAncsin´ E¨otv¨osLor´andUniversity, Faculty of Informatics, Budapest, Hungary, fdeva,koguaai,[email protected] Abstract. This paper advocates the application of language embedding for executable UML modeling. In particular, txtUML is presented, a Java API and library to build UML models using Java syntax, then run and debug them by reusing the Java runtime environment and existing de- buggers. Models can be visualized using the Papyrus editor of the Eclipse Modeling Framework and compiled to implementation languages. The paper motivates this solution, gives an overview of the language API, visualization and model compilation. Finally, implementation de- tails involving Java threads, reflection and AspectJ are presented. Keywords: executable modeling, language embedding, UML 1 Introduction Executable modeling aims at models that are completely independent of the ex- ecution platform and implementation language, and can be executed on model- level. This way models can be tested and debugged in early stages of the devel- opment process, long before every piece is in place for building and executing the software on the real target platform. Executable and platform-independent UML modeling changes the landscape of software development tools even more than mainstream modeling: graphical model editors instead of text editors, model compare and merge instead of line based compare and merge, debuggers with graphical animations instead of de- buggers for textual programs, etc. Figure 1 depicts the many different use cases such a toolset is responsible for. Models are usually persisted in a format that is hard or impossible to edit directly, therefore any kind of access to the model is dependent on different features of the modeling toolset.
    [Show full text]
  • Segédlet a Rendszermodellezés (VIMIAA00) Házi Feladathoz
    Segédlet a Rendszermodellezés (VIMIAA00) házi feladathoz Kritikus Rendszerek Kutatócsoport 2021 Tartalomjegyzék 1. Előszó 1 4.1. Yakindu projekt importálása ... 6 4.2. A modell megnyitása ........ 6 2. Alapismeretek 2 4.3. A modell kimentése ......... 6 2.1. Eclipse bevezető .......... 2 2.2. Az Eclipse munkaterület ...... 2 5. Modellezés, szimuláció 6 2.3. A Eclipse felhasználói felület ... 2 5.1. Állapot alapú modellezés ...... 6 2.4. Yakindu bevezető .......... 2 5.2. Modellezés Yakinduban ...... 7 5.3. A modell működésének szimulálása 8 3. A modellező eszköz telepítése 3 5.4. A modell működésének tesztelése . 8 3.1. Java környezet ........... 3 5.5. A modell kipróbálása ........ 9 3.2. A Yakindu telepítése létező Eclipse példányra .............. 3 5.6. Kódgenerálás ............ 9 3.3. A Yakindu telepítése a hivatalos ol- 6. Feladatkiadás és feladatbeadás 10 dalról ................ 4 6.1. HF portál használata ........ 10 3.4. Telepített verzió ellenőrzése .... 5 6.2. Az automatikus kiértékelőről ... 11 3.5. Yakindu virtuális gépen ...... 5 6.3. Tiltott elemek ............ 11 4. Projekt létrehozása, importálása 6 6.4. Ismert problémák .......... 12 Bevezetés 1. Előszó Jelen segédanyag a BME VIK elsőéves informatikus hallgatói számára készült a Méréstechnika és Információs Rendszerek Tanszéken Lucz Soma és Farkas Rebeka munkájának felhasználásával, és a Rendszermodellezés (VIMIAA00) című tárgy házi feladatainak elkészítésében segít. A Yakindu eszköz1 egy állapot alapú modellezést, szimulációt és kódgenerálást támogató eszköz. Figyelem! A szöveg a Yakindu 3.5.2-es verziójával van összhangban. Nyomatékosan kérjük, hogy idén (2021-ben) a házi feladat elkészítéséhez is ezt a verziót használják, mert más (akár újabb, akár régebbi) verziókkal kompatibilitási probléma léphet fel! 1http://statecharts.org/ 1 Rendszermodellezés Segédlet a Rendszermodellezés (VIMIAA00) házi feladathoz 2.
    [Show full text]
  • Segédlet a Rendszermodellezés (VIMIAA00) Házi Feladathoz
    Segédlet a Rendszermodellezés (VIMIAA00) házi feladathoz Kritikus Rendszerek Kutatócsoport 2021 Tartalomjegyzék 1. Előszó 2 4.1. Yakindu projekt importá- lása ............ 8 2. Alapismeretek 2 4.2. A modell megnyitása ... 8 2.1. Eclipse bevezető ..... 2 4.3. A modell kimentése .... 9 2.2. Az Eclipse munkaterület . 2 2.3. A Eclipse felhasználói fe- 5. Modellezés, szimuláció 9 lület ............ 3 5.1. Állapot alapú modellezés . 9 2.4. Yakindu bevezető ..... 3 5.2. Modellezés Yakinduban . 9 5.3. A modell működésének 3. A modellező eszköz telepíté- szimulálása ........ 11 se 4 5.4. A modell működésének 3.1. Java környezet ...... 4 tesztelése ......... 11 3.2. A Yakindu telepítése léte- 5.5. A modell kipróbálása ... 13 ző Eclipse példányra ... 4 5.6. Kódgenerálás ....... 13 3.3. A Yakindu telepítése a hi- vatalos oldalról ...... 6 6. Feladatkiadás és feladatbe- 3.4. Telepített verzió ellenőr- adás 14 zése ............ 7 6.1. HF portál használata ... 14 3.5. Yakindu virtuális gépen . 8 6.2. Az automatikus kiértéke- lőről ............ 15 4. Projekt létrehozása, impor- tálása 8 6.3. Tiltott elemek ....... 16 1 RendszermodellezésSegédlet a Rendszermodellezés (VIMIAA00) házi feladathoz 6.4. Ismert problémák ..... 17 Bevezetés 1. Előszó Jelen segédanyag a BME VIK elsőéves informatikus hallgatói számára készült a Méréstechnika és Információs Rendszerek Tanszéken Lucz Soma és Farkas Rebe- ka munkájának felhasználásával, és a Rendszermodellezés (VIMIAA00) című tárgy házi feladatainak elkészítésében segít. A Yakindu eszköz1 egy állapot alapú model- lezést, szimulációt és kódgenerálást támogató eszköz. Figyelem! A szöveg a Yakindu 3.5.2-es verziójával van összhangban. Nyo- matékosan kérjük, hogy idén (2021-ben) a házi feladat elkészítéséhez is ezt a verziót használják, mert más (akár újabb, akár régebbi) verziókkal kompati- bilitási probléma léphet fel! 2.
    [Show full text]
  • Megam@Rt2 EU Project: Open Source Tools for Mega-Modelling at Runtime of Cpss
    MegaM@Rt2 EU Project: Open Source Tools for Mega-Modelling at Runtime of CPSs 1 2 3 4 Jesus Gorroñogoitia Cruz ,​ Andrey Sadovykh ,​ Dragos Truscan ,​ Hugo Bruneliere ,​ ​ 5 ​ 1 ​ ​ Pierluigi Pierini ,​ Lara Lopez Muñiz ​ ​ 1 ATOS,​ Spain {jesus.gorronogoitia,lara.lopez}@atos.net 2 ​ Innopolis University, Russia [email protected] 3 ​ Åbo Akademi University, Finland [email protected] 4 ​ IMT Atlantique, LS2N (CNRS) & ARMINES, Nantes, France [email protected] 5 ​ Intecs Solutions S.p.A., Italy [email protected] Abstract. In this paper, we overview our experiences of developing large set of open ​ source tools in ECSEL JU European project called MegaM@Rt2 whose main objective is to propose a scalable model-based framework incorporating methods and tools for the continuous development and runtime support of complex software-intensive Cyber-Physical Systems (CPSs). We briefly present the MegaM@Rt2 concepts, discuss our approach for open source, enumerate tools and give an example of a tools selection for a specific industrial context. Our goal is to introduce the reader with open source tools for the model-based engineering of CPSs suitable for diverse industrial applications. Keywords: Model-driven engineering, Model-based system engineering, ​ Cyber-physical systems, Open Source, Tools 1 Introduction MegaM@Rt2 is a three-years project, which started in April 2017[1], [2] and which is ​ ​ ​ funded by European Components and Systems for European Leadership Joint Undertaking (ECSEL JU) under the H2020 European program. The main goal of MegaM@Rt2 is to create an integrated framework incorporating scalable methods and tools for continuous system engineering and runtime validation and verification (V&V).
    [Show full text]
  • Minisy@Dmis 2017
    PROCEEDINGS OF THE 24TH PHDMINI-SYMPOSIUM (MINISY@DMIS 2017) JANUARY 30–31, 2017 BUDAPEST UNIVERSITY OF TECHNOLOGY AND ECONOMICS BUILDING I BUDAPEST UNIVERSITY OF TECHNOLOGY AND ECONOMICS DEPARTMENT OF MEASUREMENT AND INFORMATION SYSTEMS c 2017 Department of Measurement and Information Systems, Budapest University of Technology and Economics. For personal use only – unauthorized copying is prohibited. Head of the Department: Dr. Tamas´ Daboczi´ Conference chairman: Bela´ Pataki Organizers: Csaba Debreceni Andras´ Szabolcs Nagy Andras´ Pataki Tamas´ Toth´ Homepage of the Conference: http://minisy.mit.bme.hu/ Sponsored by: Schnell Laszl´ o´ Foundation ISBN 978-963-313-243-2 FOREWORD This proceedings is a collection of the lectures of the 24th Minisymposium held at the Department of Measurement and Information Systems of the Budapest University of Technology and Economics. In the previous years the main purpose of these symposiums was to give an opportunity to the PhD students of our department to present a summary of their work done in the preceding year. It is an interesting additional benefit, that the students get some experience: how to organize such events. Beyond this actual goal, it turned out that the proceedings of our symposiums give an interesting overview of the research and PhD education carried out in our department. Last year the scope of the Minisymposium had been widened; foreign partners and some of the best MSc students were also involved. This was a real benefit, therefore, this year we have kept this widened scope. The lectures reflect partly the scientific fields and work of the students, but we think that an insight into the research and development activity of our and partner departments is also given by these contribu- tions.
    [Show full text]
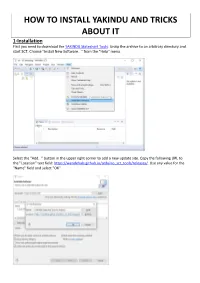
  • HOW to INSTALL YAKINDU and TRICKS ABOUT IT 1-Installation First You Need to Download the YAKINDU Statechart Tools
    HOW TO INSTALL YAKINDU AND TRICKS ABOUT IT 1-Installation First you need to download the YAKINDU Statechart Tools . Unzip the archive to an arbitrary directory and start SCT. Choose "Install New Software..." from the "Help" menu. Select the "Add..." button in the upper right corner to add a new update site. Copy the following URL to the "Location" text field: https://wendehals.github.io/arduino_sct_tools/releases/ . Use any value for the "Name" field and select "OK". Select YAKINDU Statechart Tools for Arduino and press the "Next>" button to switch to the next page. 2-Arduino Toolchain Setup Before starting development for your Arduino you need to install and setup the Arduino toolchain and libraries in your freshly installed Eclipse environment. Open the Arduino Downloads Manager from the Help menu. In the Platforms tab add a new toolchain by clicking the "Add" button and choosing the target platform. In our case it's the Arduino AVR Boards package. The Arduino toolchain and libraries are now installed. To upload the program to your Arduino you need to connect it to Eclipse. First, connect your Arduino via USB to your computer. If you have connected and used your Arduino with your computer before there should already be a driver installed. If not, make sure you have installed the Arduino IDE from arduino.cc , you need it for the USB driver. There is a wizard that helps you to create a connection to your Arduino. You can open the wizard either by choosing "New Launch Target" from the toolbar or by clicking the "New Connection" button in the "Connections" view of the C/C++ perspective.
    [Show full text]
  • Model Driven Software Development and Service Integration Lecture
    Budapest University of Technology and Economics Department of Measurement and Information Systems Fault Tolerant Systems Research Group Model Driven Software Development and Service Integration Lecture Notes and Laboratory Instructions Oszkár Semeráth Gábor Szárnyas May 10, 2013 Contents 1 Introduction 6 2 An overview of the Eclipse development environment7 2.1 Introduction.....................................................7 2.2 Project management................................................8 2.2.1 Workspace..................................................8 2.2.2 Project....................................................8 2.2.3 Package Explorer and Project Explorer.................................8 2.2.4 Build in Eclipse...............................................9 2.2.5 Copying and linking............................................9 2.2.6 Pictograms..................................................9 2.2.7 Subversion..................................................9 2.3 User interface.................................................... 10 2.3.1 Workbench.................................................. 10 2.3.2 Editors.................................................... 10 2.3.3 Views..................................................... 10 The Problems view and the Error Log view............................... 10 2.3.4 Perspective.................................................. 11 2.3.5 SWT...................................................... 11 2.3.6 Search.................................................... 11 2.4 Configuration...................................................
    [Show full text]
  • Code Generation for Sequential Constructiveness
    Christian-Albrechts-Universität zu Kiel Diploma Thesis Code Generation for Sequential Constructiveness Steven Patrick Smyth July 24, 2013 Department of Computer Science Real-Time and Embedded Systems Group Prof. Dr. Reinhard von Hanxleden Advised by: Dipl.-Inf. Christian Motika Eidesstattliche Erklärung Hiermit erkläre ich an Eides statt, dass ich die vorliegende Arbeit selbstständig verfasst und keine anderen als die angegebenen Hilfsmittel verwendet habe. Kiel, Abstract Many programming languages in the synchronous world employ a classical Model of Computation which allows them to implement determinism since they rule out race conditions. However, to do so, they impose heavy restrictions on which programs are considered valid. The newly refined Sequentially Constructive Model of Computation, developed by von Hanxleden et al. in 2012, aims to lift some of these restrictions by allowing sequential and concurrent dependent variable accesses to proceed as long as the program stays statically schedulable. The code generation approach presented in this thesis introduces a chain of key steps for deriving code automatically out of sequentially constructive statecharts, or SCCharts. It explains the intermediate language SCL, its graphical representation, the SCG, and clarifies each particular step of the transformation chain. Especially the determination of schedulability is elucidated. Additionally, pointers to optimizations are given and since the approach is embedded in the Kiel Integrated Environment for Layout Eclipse Rich Client (KIELER),
    [Show full text]
  • Introduction to Computational Techniques
    Chapter 2 Introduction to Computational Techniques Computational techniques are fast, easier, reliable and efficient way or method for solving mathematical, scientific, engineering, geometrical, geographical and statis- tical problems via the aid of computers. Hence, the processes of resolving problems in computational technique are most time step-wise. The step-wise procedure may entail the use of iterative, looping, stereotyped or modified processes which are incomparably less stressful than solving problems-manually. Sometimes, compu- tational techniques may also focus on resolving computation challenges or issues through the use of algorithm, codes or command-line. Computational technique may contain several parameters or variables that characterize the system or model being studied. The inter-dependency of the variables is tested with the system in form of simulation or animation to observe how the changes in one or more parameters affect the outcomes. The results of the simulations, animation or arrays of numbers are used to make predictions about what will happen in the real system that is being studied in response to changing conditions. Due to the adoption of computers into everyday task, computational techniques are redefined in various disciplines to accommodate specific challenges and how they can be resolved. Fortunately, computational technique encourages multi-tasking and interdisciplinary research. Since computational technique is used to study a wide range of complex systems, its importance in environmental disciplines is to aid the interpretation of field measurements with the main focus of protecting life, prop- erty, and crops. Also, power-generating companies that rely on solar, wind or hydro sources make use of computational techniques to optimize energy production when extreme climate shifts are expected.
    [Show full text]
  • A Method for Testing and Validating Executable Statechart Models
    Software & Systems Modeling https://doi.org/10.1007/s10270-018-0676-3 THEME SECTION PAPER A method for testing and validating executable statechart models Tom Mens1 · Alexandre Decan1 · Nikolaos I. Spanoudakis2 Received: 29 August 2016 / Accepted: 11 April 2018 © Springer-Verlag GmbH Germany, part of Springer Nature 2018 Abstract Statecharts constitute an executable language for modelling event-based reactive systems. The essential complexity of statechart models solicits the need for advanced model testing and validation techniques. In this article, we propose a method aimed at enhancing statechart design with a range of techniques that have proven their usefulness to increase the quality and reliability of source code. The method is accompanied by a process that flexibly accommodates testing and validation techniques such as test-driven development, behaviour-driven development, design by contract, and property statecharts that check for violations of behavioural properties during statechart execution. The method is supported by the Sismic tool, an open-source statechart interpreter library in Python, which supports all the aforementioned techniques. Based on this tool- ing, we carry out a controlled user study to evaluate the feasibility, usefulness and adequacy of the proposed techniques for statechart testing and validation. Keywords Statechart · Executable modeling · Behaviour-driven development · Design by contract · Runtime verification 1 Introduction cial tools such as IBM Rational’s StateMate and Rhapsody, the Mathworks’ Stateflow, itemis’ Yakindu Statechart Tools Statecharts were introduced nearly three decades ago by and IAR Systems’ visualSTATE. There are also multiple Harel [27,28] as a visual executable modelling language. open-source frameworks defining domain-specific languages From a formal point of view, they can be considered as (DSLs) based on statecharts, such as the ATOMPM [47] web- an extension of hierarchical finite-state machines with char- based domain-specific modelling environment with support acteristics of both Mealy and Moore automata.
    [Show full text]
  • Statecharts.Pdf
    AperTO - Archivio Istituzionale Open Access dell'Università di Torino On checking delta-oriented product lines of statecharts This is the author's manuscript Original Citation: Availability: This version is available http://hdl.handle.net/2318/1671322 since 2018-12-16T17:13:33Z Published version: DOI:10.1016/j.scico.2018.05.007 Terms of use: Open Access Anyone can freely access the full text of works made available as "Open Access". Works made available under a Creative Commons license can be used according to the terms and conditions of said license. Use of all other works requires consent of the right holder (author or publisher) if not exempted from copyright protection by the applicable law. (Article begins on next page) 06 October 2021 On checking delta-oriented product lines of statecharts I Michael Lienhardta, Ferruccio Damiania,∗, Lorenzo Testaa, Gianluca Turina aUniversity of Torino, Italy ([email protected], [email protected], {lorenzo.testa, gianluca.turin}@edu.unito.it) Abstract A Software Product Line (SPL) is a set of programs, called variants, which are generated from a common artifact base. Delta-Oriented Programming (DOP) is a flexible approach to implement SPLs. In this article, we provide a foundation for rigorous development of delta-oriented product lines of statecharts. We introduce a core language for statecharts, we define DOP on top of it, we present an analysis ensuring that a product line is well-formed (i.e., all variants can be generated and are well-formed statecharts), and we illustrate how an implementation of the analysis has been applied to an industrial case study.
    [Show full text]
  • Extending Kouretes Statechart Editor for Executing Statechart-Based Robotic Behavior Models
    Technical University of Crete School of Electronic and Computer Engineering Extending Kouretes Statechart Editor for Executing Statechart-Based Robotic Behavior Models Georgios L. Papadimitriou Thesis Committee Associate Professor Michail G. Lagoudakis Assistant Professor Vasileios Samoladas Dr. Nikolaos Spanoudakis Chania, July 2014 Πολυτεχνείο Κρήτης Σχολή Ηλεκτρονικών Μηχανικών και Μηχανικών Υπολογιστών Αναβάθμιση του Kouretes Statechart Editor για Εκτέλεση Μοντέλων Ρομποτικής Συμπεριφοράς Βασισμένων σε Διαγράμματα Καταστάσεων Γεώργιος Λ. Παπαδημητρίου Εξεταστική Επιτροπή Αναπληρωτής Καθηγητής Μιχαήλ Γ. Λαγουδάκης Επίκουρος Καθηγητής Βασίλειος Σαμολαδάς Δρ. Νικόλαος Σπανουδάκης Χανιά, Ιούλιος 2014 Acknowledgements First of all, I would like to thank my family for their love and support during my long years of studying towards achieving my engineering Diploma. I would also like to give extra thanks to my brother Panos who's been a great asset to me and constantly helps me in every stage of my life, since I can remember myself. Next, I would like to thank my grandparents for their great support, and my aunt Catherine Geronikolou for helping me in any possible way during my thesis implementation. Moreover, I would like to thank my thesis supervisor, Dr. Michail G. Lagoudakis, for trusting me in investigating this diploma thesis topic, giving me the opportunity to work in my favorite scientific field. Another person I would like to thank, is my co-supervisor, Dr. Nikolaos Spanoudakis, for his exceptional help and willingness to aid me throughout the completion of my thesis. I would like to give exceptional thanks to my father, whose advices and self-sacrifices during the years made me realize in an early stage of my life, that you should be patient and work very hard in order to fulfill your ambitions.
    [Show full text]