DOCSLIB.ORG

Effects of Stream Temperature and Climate Change On

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Effects of Stream Temperature and Climate Change On EFFECTS OF STREAM TEMPERATURE AND CLIMATE CHANGE ON FLUVIAL ARCTIC GRAYLING AND NON-NATIVE SALMONIDS IN THE UPPER BIG HOLE RIVER, MONTANA by Shane Jeffrey Vatland A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Fish and Wildlife Biology MONTANA STATE UNIVERSITY Bozeman, Montana December 2015 ©COPYRIGHT by Shane Jeffrey Vatland 2015 All Rights Reserved ii DEDICATION This dissertation is dedicated to my loving and supportive family and friends. iii ACKNOWLEDGEMENTS I thank my mentor and co-advisor Dr. Robert Gresswell for his guidance throughout this process. I thank Dr. Al Zale, my co-advisor and committee chair, for his unwavering support and critical contribution to my graduate studies at Montana State University. Dr. Wyatt Cross and Dr. Jeff Kershner provided valuable feedback on all my writing and were very supportive throughout this endeavor. I would also like to thank Dr. Paul Gannon for participating as my graduate school representative. Overall, my graduate advising committee was extremely helpful in guiding my dissertation research and doctoral student experience. I would like to thank Montana Fish, Wildlife & Parks, numerous field staff, and many volunteers for acquiring and organizing field and lab data. I would also like to thank my graduate student peers for their many thoughtful contributions. Dr. Daniel Isaak, Dr. Geoff Poole, and Dr. Steve Hostetler all provided critical inputs to my dissertation. Dr. Doug Peterson was also very supportive and helped enable this research project. Funding to support this project was provided by U.S. Geological Survey, Big Hole Watershed Committee, Montana Water Center—Wild Fish Habitat Initiative, Arctic Grayling Recovery Program, and Montana Trout Unlimited. Graduate student fellowships from the Montana Institute on Ecosystems and Montana Water Center partially supported the analysis of these data. iv TABLE OF CONTENTS 1. INTRODUCTION ...........................................................................................................1 References ........................................................................................................................6 2. QUANTIFYING STREAM THERMAL REGIMES AT MULTIPLE SCALES: COMBINING THERMAL INFRARED IMAGERY AND STATIONARY STREAM TEMPERATURE DATA IN A NOVEL MODELING FRAMEWORK .........................................................................................8 Contributions of Author and Co-Authors ........................................................................8 Manuscript Information Page ..........................................................................................9 Abstract ..........................................................................................................................10 Introduction ....................................................................................................................10 Methods..........................................................................................................................11 Study Area .............................................................................................................11 Data Collection and Processing .............................................................................12 Stationary Temperature Loggers................................................................12 Airborne Thermal Infrared (TIR)...............................................................13 Langrangian Longitudinal Thermal Profiling ............................................13 Geographic Information System (GIS) ......................................................13 Modeling Summer Stream Temperature ................................................................13 General Approach ......................................................................................13 Predicting Subdaily Mean Stream Temperature ........................................14 Developing A Modified Sine Model..........................................................14 Evaluating Model Performance .................................................................16 Model Sensitivity Analysis ........................................................................16 Applying the Model to Management Criteria ............................................16 Results ............................................................................................................................17 TIR Accuracy and Stationary Loggers ..................................................................17 Predicting Subdaily Mean Stream Temperature Longitudinal Profiles .................17 Development of the TIR-Based Sine Model ..........................................................17 TIR-Based Sine Model Evaluation ........................................................................18 Model Sensitivity ...................................................................................................18 Comparing the Model to Management Criteria .....................................................19 Discussion ......................................................................................................................19 Integrating TIR and Stationary Stream Temperature Data ....................................19 Model Evaluation ...................................................................................................20 From Theory to Application ..................................................................................23 Conclusions ....................................................................................................................23 References ......................................................................................................................24 v TABLE OF CONTENTS - CONTINUED 3. EFFECTS OF CLIMATE CHANGE ON THE THERMAL HABITATS OF ARCTIC GRAYLING AND NON-NATIVE SALMONIDS ................................................................................................................26 Contributions of Author and Co-Authors ......................................................................26 Manuscript Information Page ........................................................................................27 Title Page .......................................................................................................................28 Abstract ..........................................................................................................................29 Introduction ....................................................................................................................30 Materials and Methods ...................................................................................................32 Study Area, Focal Species, and Thermal Tolerance Thresholds ...........................32 Water Temperature Modeling Overview ...............................................................35 Stream Water and Air Temperature Measurements...............................................36 Site-specific Climate Forcing on Water Temperature ...........................................37 Future Air Temperature Scenarios .........................................................................39 Modeling Site-Specific Water Temperature Change Over Time ..........................42 Modeling Spatial Patterns of Summer Water Temperature ...................................42 Combining Models to Predict Water Temperature Across Space and Time .........45 Results ............................................................................................................................47 Air-Water Temperature Relationships ...................................................................47 Air Temperature Changes ......................................................................................47 Projected Changes in Summer Water Temperatures at Observation Sites ............48 Spatial Predictors of Summer Water Temperatures ...............................................49 Projected Changes in Summer Water Temperatures Throughout the Study Area ....................................................................................50 Discussion ......................................................................................................................52 Acknowledgements ........................................................................................................59 References ......................................................................................................................69 4. CONCLUSIONS............................................................................................................80 References ......................................................................................................................84 REFERENCES CITED ......................................................................................................86 APPENDICES .................................................................................................................103 APPENDIX A: Supporting Information for Chapter 2........................................104 APPENDIX B: Supporting Information for Chapter 3 ........................................112 vi LIST OF TABLES Table Page 2.1. Goodness-of-Fit Metrics from Internal and External Model Evaluation .......19 3.1. Site-specific linear regressions using weekly mean daily maximum (WMDM) air temperature (°C) as
Load more

Recommended publications
  • Big Hole River Fluvial Arctic Grayling
    FLUVIAL ARCTIC GRAYLING MONITORING REPORT 2003 James Magee and Peter Lamothe Montana Department of Fish, Wildlife and Parks Dillon, Montana Submitted To: Fluvial Arctic Grayling Workgroup And Beaverhead National Forest Bureau of Land Management Montana Chapter, American Fisheries Society Montana Council, Trout Unlimited Montana Department of Fish, Wildlife, and Parks U. S. Fish and Wildlife Service June 2004 ACKNOWLEDGMENTS The following individuals and organizations contributed valuable assistance to the project in 2003. Scott Lula, Greg Gibbons, Zachary Byram, Tracy Elam, Tim Mosolf, and Dick Oswald of Montana Fish, Wildlife, and Parks (FWP), provided able field assistance. Ken Staigmiller (FWP) collected samples for disease testing. Ken McDonald (FWP), provided administrative support, chaired the Fluvial Arctic Grayling Workgroup, reviewed progress reports and assisted funding efforts. Bob Snyder provided support as Native Species Coordinator. Dick Oswald (FWP) provided technical advice and expertise. Bruce Rich (FWP) provided direction as regional fisheries supervisor. Jim Brammer, Dennis Havig, Dan Downing, and Chris Riley (USFS) assisted with funding, provided housing for FWP technicians, and assisted with fieldwork. Bill Krise, and Ron Zitzow, Matt Toner, and the staff of the U.S. Fish and Wildlife Service (USFWS) Bozeman Fish Technology Center maintained the brood reserve stock and transported grayling to the upper Ruby River. Jack Boyce, Mark Kornick and Jim Drissell, and crew of Big Springs Hatchery assisted with egg takes at Axolotl and Green Hollow II brood lakes, and transported eyed grayling eggs for RSI use in the upper Ruby River and to Bluewater State Fish Hatchery for rearing reaches. Gary Shaver, Bob Braund, and Dave Ellis from Bluewater State Hatchery raised and transported grayling to the Ruby River and the Missouri Headwaters restoration reaches.
    [Show full text]
  • Likely to Have Habitat Within Iras That ALLOW Road
    Item 3a - Sensitive Species National Master List By Region and Species Group Not likely to have habitat within IRAs Not likely to have Federal Likely to have habitat that DO NOT ALLOW habitat within IRAs Candidate within IRAs that DO Likely to have habitat road (re)construction that ALLOW road Forest Service Species Under NOT ALLOW road within IRAs that ALLOW but could be (re)construction but Species Scientific Name Common Name Species Group Region ESA (re)construction? road (re)construction? affected? could be affected? Bufo boreas boreas Boreal Western Toad Amphibian 1 No Yes Yes No No Plethodon vandykei idahoensis Coeur D'Alene Salamander Amphibian 1 No Yes Yes No No Rana pipiens Northern Leopard Frog Amphibian 1 No Yes Yes No No Accipiter gentilis Northern Goshawk Bird 1 No Yes Yes No No Ammodramus bairdii Baird's Sparrow Bird 1 No No Yes No No Anthus spragueii Sprague's Pipit Bird 1 No No Yes No No Centrocercus urophasianus Sage Grouse Bird 1 No Yes Yes No No Cygnus buccinator Trumpeter Swan Bird 1 No Yes Yes No No Falco peregrinus anatum American Peregrine Falcon Bird 1 No Yes Yes No No Gavia immer Common Loon Bird 1 No Yes Yes No No Histrionicus histrionicus Harlequin Duck Bird 1 No Yes Yes No No Lanius ludovicianus Loggerhead Shrike Bird 1 No Yes Yes No No Oreortyx pictus Mountain Quail Bird 1 No Yes Yes No No Otus flammeolus Flammulated Owl Bird 1 No Yes Yes No No Picoides albolarvatus White-Headed Woodpecker Bird 1 No Yes Yes No No Picoides arcticus Black-Backed Woodpecker Bird 1 No Yes Yes No No Speotyto cunicularia Burrowing
    [Show full text]
  • Memorandum of Understanding Concerning Montana Arctic
    Memorandum of Understanding Concerning Montana Arctic Grayling Restoration August 2007 1 MEMORANDUM OF UNDERSTANDING among: MONTANA FISH, WILDLIFE & PARKS (FWP) U.S. BUREAU OF LAND MANAGEMENT (BLM) U.S. FISH & WILDLIFE SERVICE (USFWS) U.S. FOREST SERVICE (USFS) MONTANA COUNCIL TROUT UNLIMITED (TU) MONTANA CHAPTER AMERICAN FISHERIES SOCIETY (AFS) YELLOWSTONE NATIONAL PARK (YNP) MONTANA ARCTIC GRAYLING RECOVERY PROGRAM (AGRP) USDA NATURAL RESOURCE CONSERVATION SERVICE (NRCS) MONTANA DEPARTMENT OF NATURAL RESOURCES AND CONSERVATION (DNRC) concerning MONTANA ARCTIC GRAYLING RESTORATION BACKGROUND Montana’s Arctic grayling Thymallus arcticus is a unique native species that comprises an important component of Montana’s history and natural heritage. Fluvial (river dwelling) Arctic grayling were once widespread in the Missouri River drainage, but currently wild grayling persist only in the Big Hole River, representing approximately 4% of their native range in Montana. Native lacustrine/adfluvial populations historically distributed in the Red Rock drainage and possibly the Big Hole drainage have also been reduced in abundance and distribution. Arctic grayling have a long history of being petitioned for listing under the Endangered Species Act (ESA). Most recently (in April 2007) the U. S. Fish and Wildlife Service (USFWS) determined that listing of Arctic grayling in Montana under ESA was not warranted because it does not constitute a distinct population segment as defined by the ESA. On May 15th 2007, the Center for Biological Diversity announced its 60-day Intent to Sue the USFWS regarding the recent grayling decision. The Montana Arctic Grayling Recovery Program (AGRP) was formed in 1987 following declines in the Big Hole River Arctic grayling population, and over concerns for the Red Rock population.
    [Show full text]
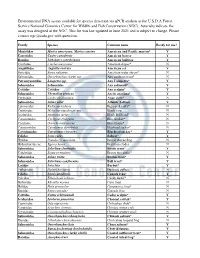
  • Edna Assay Development
    Environmental DNA assays available for species detection via qPCR analysis at the U.S.D.A Forest Service National Genomics Center for Wildlife and Fish Conservation (NGC). Asterisks indicate the assay was designed at the NGC. This list was last updated in June 2021 and is subject to change. Please contact [email protected] with questions. Family Species Common name Ready for use? Mustelidae Martes americana, Martes caurina American and Pacific marten* Y Castoridae Castor canadensis American beaver Y Ranidae Lithobates catesbeianus American bullfrog Y Cinclidae Cinclus mexicanus American dipper* N Anguillidae Anguilla rostrata American eel Y Soricidae Sorex palustris American water shrew* N Salmonidae Oncorhynchus clarkii ssp Any cutthroat trout* N Petromyzontidae Lampetra spp. Any Lampetra* Y Salmonidae Salmonidae Any salmonid* Y Cottidae Cottidae Any sculpin* Y Salmonidae Thymallus arcticus Arctic grayling* Y Cyrenidae Corbicula fluminea Asian clam* N Salmonidae Salmo salar Atlantic Salmon Y Lymnaeidae Radix auricularia Big-eared radix* N Cyprinidae Mylopharyngodon piceus Black carp N Ictaluridae Ameiurus melas Black Bullhead* N Catostomidae Cycleptus elongatus Blue Sucker* N Cichlidae Oreochromis aureus Blue tilapia* N Catostomidae Catostomus discobolus Bluehead sucker* N Catostomidae Catostomus virescens Bluehead sucker* Y Felidae Lynx rufus Bobcat* Y Hylidae Pseudocris maculata Boreal chorus frog N Hydrocharitaceae Egeria densa Brazilian elodea N Salmonidae Salvelinus fontinalis Brook trout* Y Colubridae Boiga irregularis Brown tree snake*
    [Show full text]
  • Spawning and Early Life History of Mountain Whitefish in The
    SPAWNING AND EARLY LIFE HISTORY OF MOUNTAIN WHITEFISH IN THE MADISON RIVER, MONTANA by Jan Katherine Boyer A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Fish and Wildlife Management MONTANA STATE UNIVERSITY Bozeman, Montana January 2016 © COPYRIGHT by Jan Katherine Boyer 2016 All Rights Reserved ii ACKNOWLEDGMENTS First, I thank my advisor, Dr. Christopher Guy, for challenging me and providing advice throughout every stage of this project. I also thank my committee members, Dr. Molly Webb and Dr. Tom McMahon, for guidance and suggestions which greatly improved this research. My field technicians Jordan Rowe, Greg Hill, and Patrick Luckenbill worked hard through fair weather and snowstorms to help me collect the data presented here. I also thank Travis Horton, Pat Clancey, Travis Lohrenz, Tim Weiss, Kevin Hughes, Rick Smaniatto, and Nick Pederson of Montana Fish, Wildlife and Parks for field assistance and advice. Mariah Talbott, Leif Halvorson, and Eli Cureton of the U. S. Fish and Wildlife Service assisted with field and lab work. Richard Lessner and Dave Brickner at the Madison River Foundation helped to secure funding for this project and conduct outreach in the Madison Valley. The Channels Ranch, Valley Garden Ranch, Sun West Ranch, and Galloup’s Slide Inn provided crucial land and river access. I also thank my fellow graduate students both for advice on project and class work and for being excellent people to spend time with. Ann Marie Reinhold, Mariah Mayfield, David Ritter, and Peter Brown were especially helpful during the early stages of this project.
    [Show full text]
  • Native Fish Conservation
    Yellowstone SScience Native Fish Conservation @ JOSH UDESEN Native Trout on the Rise he waters of Yellowstone National Park are among the most pristine on Earth. Here at the headwaters of the Missouri and Snake rivers, the park’s incredibly productive streams and lakes support an abundance of fish. Following the last Tglacial period 8,000-10,000 years ago, 12 species/subspecies of fish recolonized the park. These fish, including the iconic cutthroat trout, adapted and evolved to become specialists in the Yellowstone environment, underpinning a natural food web that includes magnificent animals: ospreys, bald eagles, river otters, black bears, and grizzly bears all feed upon cutthroat trout. When the park was established in 1872, early naturalists noted that about half of the waters were fishless, mostly because of waterfalls which precluded upstream movement of recolonizing fishes. Later, during a period of increasing popularity of the Yellowstone sport fishery, the newly established U.S. Fish Commission began to extensively stock the park’s waters with non-natives, including brown, brook, rainbow, and lake trout. Done more than a century ago as an attempt to increase an- gling opportunities, these actions had unintended consequences. Non-native fish caused serious negative impacts on native fish populations in some watersheds, and altered the parks natural ecology, particularly at Yellowstone Lake. It took a great deal of effort over many decades to alter our native fisheries. It will take a great deal more work to restore them. As Aldo Leopold once said, “A thing is right when it tends to preserve the integrity, stability, and beauty of the biotic com- munity.
    [Show full text]
  • Kenai National Wildlife Refuge Species List, Version 2018-07-24
    Kenai National Wildlife Refuge Species List, version 2018-07-24 Kenai National Wildlife Refuge biology staff July 24, 2018 2 Cover image: map of 16,213 georeferenced occurrence records included in the checklist. Contents Contents 3 Introduction 5 Purpose............................................................ 5 About the list......................................................... 5 Acknowledgments....................................................... 5 Native species 7 Vertebrates .......................................................... 7 Invertebrates ......................................................... 55 Vascular Plants........................................................ 91 Bryophytes ..........................................................164 Other Plants .........................................................171 Chromista...........................................................171 Fungi .............................................................173 Protozoans ..........................................................186 Non-native species 187 Vertebrates ..........................................................187 Invertebrates .........................................................187 Vascular Plants........................................................190 Extirpated species 207 Vertebrates ..........................................................207 Vascular Plants........................................................207 Change log 211 References 213 Index 215 3 Introduction Purpose to avoid implying
    [Show full text]
  • Summary Report No
    Canadian Manuscript Report of Fisheries and Aquatic Sciences 2614 2002 Life History Characteristics Of Freshwater Fishes Occurring in the Northwest Territories and Nunavut, With Major Emphasis on Riverine Habitat Requirements by C.L. Evans1, J.D. Reist1 and C.K. Minns2 1. Department of Fisheries and Oceans, Arctic Fish Ecology and Assessment Research, Central and Arctic Division, 501 University Crescent, Winnipeg, Manitoba, R3T 2N6 Canada 2. Department of Fisheries and Oceans, Great Lakes Laboratory of Fisheries and Aquatic Sciences, Bayfield Institute, 867 Lakeshore Road, P.O. Box 5050, Burlington, Ontario, L7R 4A6 Canada. Her Majesty the Queen in Right of Canada, 2002 Cat. No. Fs 97-4/2614E ISSN 0706-6473 Correct citation of this publication: Evans, C.E., J.D. Reist and C.K. Minns. 2002. Life history characteristics of freshwater fishes occurring in the Northwest Territories and Nunavut, with major emphasis on riverine habitat requirements. Can. MS Rep. Fish. Aquat. Sci. 2614: xiii + 169 p. ii TABLE OF CONTENTS LIST OF FIGURES .......................................................................................................... v LIST OF TABLES............................................................................................................ v ABSTRACT ...................................................................................................................viii RÉSUMÉ ........................................................................................................................viii INTRODUCTION............................................................................................................
    [Show full text]
  • Arctic Grayling
    Arctic Grayling For most anglers in America, the Arctic grayling (Thymallus arcticus (Pallus)) is a rare freshwater game fish symbolic of the clear, cold streams of the northern wilderness. Grayling occur throughout the arctic as far west as the Kara River in Russia and east to the western shores of Hudson Bay in Canada. Once as common as far south as Michigan and Montana, the Arctic grayling has almost disappeared from the northern United States because of overfishing, competition from introduced species, and habitat loss. General description: The Arctic grayling is an elegantly formed cousin of the trout. With its sail-like dorsal fin dotted with large iridescent red or purple spots, the grayling is one of the most unusual and beautiful fish of Alaska. Grayling are generally dark on the back and have iridescent gray sides. They have varying numbers of black spots scattered along the anterior portion of both sides. The adipose, caudal (tail), pectoral, and anal fins are gray and the pelvic fins are often marked with pink to orange stripes. Life history: Grayling have evolved many strategies to meet the needs of life in what are often harsh and uncertain environments. Grayling can be highly migratory, using different streams for spawning, juvenile rearing, summer feeding, and overwintering. Or, in other areas, they can complete their entire life without leaving a short section of stream or lake. Winter generally finds grayling in lakes or the deeper pools of medium-sized rivers such as the Chena and Gulkana, or in large glacial rivers like the Tanana, Susitna, and Yukon.
    [Show full text]
  • Diving Ducks
    Avian Models for 3D Applications Characters and Texture Mapping by Ken Gilliland 1 Songbird ReMix Waterfowl: Sea & Diving Ducks Contents Introduction 3 Overview 3 Poser and DAZ Studio Use 3 Physical-based Renderers 4 Where to find your birds 4 Morphs and their Use 5 Field Guide List of Species 10 Diving Ducks Red-crested Pochard 11 Pink-headed Duck (extinct) 13 Redhead 16 Tufted Duck 18 Lesser Scaup 21 Greater Scaup 25 Hardhead 28 Ferruginous Duck 30 Sea Ducks King Eider 32 Harlequin Duck 34 Black Scoter 36 Smew 38 Common Goldeneye 40 Bufflehead 42 Hooded Merganser 44 Chinese Merganser 46 Ruddy Duck 49 Resources, Credits and Thanks 51 Appendix 52 Copyrighted 2014-18 by Ken Gilliland www.songbirdremix.com Opinions expressed on this booklet are solely that of the author, Ken Gilliland, and may or may not reflect the opinions of the publisher. 2 Songbird ReMix Waterfowl: Sea & Diving Ducks Introduction There are two distinct groups of Ducks; Dabbling Ducks and Sea/Diving Ducks. They are divided into the two groups mostly by behavior. Diving ducks and sea ducks forage deep underwater. To be able to submerge more easily, the diving ducks are heavier than dabbling ducks, and therefore have more difficulty taking off to fly. Diving ducks are commonly called pochards or scaups, while Sea ducks have a much larger family of species including eiders, scoters, mergansers, goldeneyes and other species. Most of these ducks occupy habitats in the northern latitudes. Overview The set is located within the Animals : Songbird ReMix folder. Here is where you will find a number of folders, such as Bird Library, Manuals and Resources .
    [Show full text]
  • Population Viability of Arctic Grayling in the Gibbon River, Yellowstone National Park
    North American Journal of Fisheries Management 30:1582–1590, 2010 [Article] Ó Copyright by the American Fisheries Society 2010 DOI: 10.1577/M10-083.1 Population Viability of Arctic Grayling in the Gibbon River, Yellowstone National Park 1 AMBER C. STEED* Montana Cooperative Fishery Research Unit and Department of Ecology, Montana State University, Post Office Box 173460, Bozeman, Montana 59717, USA ALEXANDER V. ZALE U.S. Geological Survey, Montana Cooperative Fishery Research Unit, and Department of Ecology, Montana State University, Post Office Box 173460, Bozeman, Montana 59717, USA TODD M. KOEL Fisheries and Aquatic Sciences Program, Yellowstone Center for Resources, Post Office Box 168, Yellowstone National Park, Wyoming 82190, USA STEVEN T. KALINOWSKI Department of Ecology, Montana State University, Post Office Box 172460, Bozeman, Montana 59717, USA Abstract.—The fluvial Arctic grayling Thymallus arcticus is restricted to less than 5% of its native range in the contiguous United States and was relisted as a category 3 candidate species under the U.S. Endangered Species Act in 2010. Although fluvial Arctic grayling of the lower Gibbon River, Yellowstone National Park, Wyoming, were considered to have been extirpated by 1935, anglers and biologists have continued to report catching low numbers of Arctic grayling in the river. Our goal was to determine whether a viable population of fluvial Arctic grayling persisted in the Gibbon River or whether the fish caught in the river were downstream emigrants from lacustrine populations in headwater lakes. We addressed this goal by determining relative abundances, sources, and evidence for successful spawning of Arctic grayling in the Gibbon River.
    [Show full text]
  • Appendix 14 CSKT Sensitive Species and Heritage Program Ranks for Species in the Flathead Subbasin
    Appendix 14 CSKT Sensitive Species and Heritage Program Ranks for Species in the Flathead Subbasin Confederated Salish and Kootenai Tribes (CSKT) Sensitive Terrestrial Species List The tribes and state classify 39 terrestrial, vertebrate wildlife species in the subbasin as sensitive (table xx). All are considered sensitive due to low populations, threats to their habitats, or highly restricted distributions. These species do not necessarily have legal protection but are considered sensitive to human activities and attention to their habitat and population needs may be warranted during the planning of resource management activities. The status of many of these species is not known because there have been few population or habitat studies. Table 1. CSKT sensitive terrestrial species Amphibians Boreal toad Tailed frog Birds Common loon Common tern American white pelican Forster’s tern Black-crowned night-heron Black tern White-faced ibis Yellow-billed cuckoo Trumpeter swan Flammulated owl Harlequin duck Burrowing owl Bald eagle Great gray owl Northern goshawk Boreal owl Ferruginous hawk Black swift Peregrine falcon Black-backed woodpecker Columbian sharp-tailed grouse Loggerhead shrike Black-necked stilt Baird’s sparrow Franklin’s gull Le conte’s sparrow Caspian tern Mammals Townsend’s big-eared bat Woodland caribou Northern bog lemming Wolverine Gray wolf Fisher Grizzly bear River Otter Lynx Montana Natural Heritage Program Ranks Species have been evaluated and ranked on the basis of their global (range-wide) status, and their Montana-wide status, using the standardized ranking system of the Natural Heritage Network (NatureServe 2003). Species on the list may be common elsewhere but rare in Montana because they are on the margin of their range.
    [Show full text]