DOCSLIB.ORG

LIB1RARIES [Except for This Sentence, This Page Intentionally Left Blank.] RPMEBW

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
LIB1RARIES [Except for This Sentence, This Page Intentionally Left Blank.] RPMEBW Optimal Orbital Transfer Using a Legendre Pseudospectral Method by Stuart Andrew Stanton B.S. Astronautical Engineering United States Air Force Academy, 2001 SUBMITTED TO THE DEPARTMENT OF AERONAUTICS AND ASTRONAUTICS IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN AERONAUTICS AND ASTRONAUTICS at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY JUNE 2003 @2003 Stuart Andrew Stanton. All rights reserved. The author hereby grants to MIT permission to reproduce and to distribute publicly paper and electronic copies of this thesis document in whole or in part. Signature of Author. Department of Aeronautics and Astronautics May 23, 2003 Certified by Christop er N. D'Souza, Ph.D. The Charles Stark Draper Laboratory, Inc. Thesis Supervisor Certified by Ronald J. Proulx, Ph.D. The Charles Stark Draper Laboratory, Inc. - ,Thesis Supervisor Certified by George T. Schmidt, Sc.D. Lecturer, Department of Aeronautics and Astronautics Director, Education The Charles Stark Draper Laboratory, Inc. Thesis Advisor Accepted by Edward M. Greitzer, Ph.D. H.N. Slater Professor of Aeronautics and Astronautics Chair, Committee on Graduate Students MASSAPiHuIIiiTUTn ()F TECHNM1.0GY AERO ep~IR E2S3 LIB1RARIES [Except for this sentence, this page intentionally left blank.] RPMEBW Optimal Orbital Transfer Using a Legendre Pseudospectral Method by Stuart A. Stanton Submitted to the Department of Aeronautics and Astronautics on May 23, 2003, in partial fulfillment of the requirements for the degree of Master of Science in Aeronautics and Astronautics Abstract Orbital transfer problems are solved successfully for several classes of transfers, in- cluding coplanar transfer, simple plane change, and complex orbital size/shape/plane changes. Both impulsive and finite-burn orbital transfers are constructed which mini- mize fuel costs. Using the direct Legendre pseudospectral technique software package (DIDO) developed by Ross and Fahroo of the Naval Postgraduate School, the effects of complex perturbations (like J2) are naturally included in the optimal solution. Written in Matlab, the DIDO package allows the user to incorporate complex cost functions, bounds, and constraints on the optimal transfer trajectory through a stan- dardized interface. Thesis Supervisor: Christopher N. D'Souza, Ph.D. Title: The Charles Stark Draper Laboratory, Inc. Thesis Supervisor: Ronald J. Proulx, Ph.D. Title: The Charles Stark Draper Laboratory, Inc. Thesis Advisor: George T. Schmidt, Sc.D. Title: Lecturer, Department of Aeronautics and Astronautics Director, Education The Charles Stark Draper Laboratory, Inc. 3 [Except for this sentence, this page intentionally left blank.] ACKNOWLEDGMENT May 23, 2003 This thesis could not have been written without the help of a number of different people and organizations. Thank you to everyone that has in any way contributed to making it possible for me to succeed. Thanks to the Charles Stark Draper Laboratory for the opportunity to work as a Draper Fellow for two years. My appreciation goes to all of the staff members that I have had the privilege of working with while I was here. Thanks to Tim Brand for providing direction for this research. A special thank you to Chris D'Souza and Ron Proulx for their wisdom and expertise. Chris, thank you for sticking with me from afar. Ron, thank you for putting up with me from anear. Both of you have provided me with so much technical support; I would have been lost without the benefit of your experience and knowledge. Thanks to my fellow Fellows, especially my officemates: Ted Dyckman, Stephen Long, David Woffinden, Kimberley Clarke, Christine Taylor. It was a trip. Ted, thanks for showing me the ropes and helping me get my feet wet. Steve, thanks for the comedy and thanks for being there. Dave, thanks for being the "grown-up" in our office. Thanks to Matt Obenchain for being a good friend and study partner. John Young, thanks for reminding me to lock my computer. Jen DiCarlo, thanks for the free food. Good luck to everyone in their future lives. Thanks to those in my life outside of the lab. To my parents, words cannot begin to express my gratitude. To my brother, Spencer, thanks for helping me get settled out here. Margaret O'Keefe, thank you for being my mentor. Thanks to the Air Force Institute of Technology for the opportunity to pursue a graduate degree. Thank you to Col Jack Anthony and LtCol Jerry Sellers for guiding my career as I prepare to finally join the Real Air Force. This thesis was prepared at The Charles Stark Draper Laboratory, Inc., under Draper Internal Research and Development Project 15269, GCDLF Support. Publication of this thesis does not constitute approval by Draper or the sponsor- ing agency of the findings or conclusions contained herein. It is published for the exchange and stimulation of ideas. Star&U. Stanton, 2Lt., USAF 5 [Except for this sentence, this page intentionally left blank.] Contents 1 Introduction 15 1.1 M otivation ... ..... ...... ..... ..... ..... 15 1.2 Background ..... ..... ...... ..... ..... .. 16 1.3 Thesis Overview ....... ....... ....... ..... 17 2 Optimal Control Theory 21 2.1 Function Minimization .... ...... ..... ..... .. 21 2.2 Functional Minimization . ..... ...... ..... .... 25 2.3 The Optimal Control Problem . ...... ...... ..... 27 2.3.1 Pontryagin's Minimum Principle ...... ...... 28 3 Numerical Methods for Solving Optimal Control Problems 31 3.1 Numerical Techniques .. ..... ...... ..... ..... ... 3 2 3.1.1 Lagrange Interpolation ......... 33 3.1.2 Orthogonal Functions .......... 34 3.1.3 Gaussian Quadrature .......... 36 3.2 Direct Optimization Methods .. ..... .. 37 3.2.1 Collocation Methods . ..... .... 37 3.2.2 Spectral Methods ... .... .... 40 3.2.3 The Legendre Pseudospectral Method . 42 4 General DIDO Problem Setup 45 4.1 Functions . ...... .... 45 4.1.1 Main Function . .. 45 4.1.2 Cost Function .. ... 48 4.1.3 Dynamics Function .. 48 4.1.4 Events Function . ... 48 4.1.5 Path Function .. ... 49 4.2 Scaling ..... ........ 49 5 Orbital Transfer Optimization 51 5.1 Problem Dynamics ...... ..... .. 51 5.1.1 State Definitions .. ..... 51 7 5.1.2 Perturbations .................... .. 54 5.1.3 Controls .......... ............. .. 57 5.2 The Performance Index ................... .. .. 58 5.3 Event Constraints ...................... .. 59 5.4 Design Choices for Specific Problems ........... .. 60 5.4.1 Pure Impulses .................. .. .. .. .. 60 5.4.2 High Thrust Impulsive Approximation . ..... .. .. ... 61 5.4.3 Finite-Burn ......... ......... ... .. ... .. 61 5.5 Other Tools ...... .......... ......... ... .. 62 6 Impulsive Burn Orbital Transfer 63 6.1 Capability Demonstration ................. 64 6.1.1 Hohmann Transfer ........... ...... 64 6.1.2 Plane Change .................... 70 6.1.3 Combined Plane Change ..... ......... 80 6.1.4 The J2 Perturbation. ................ 86. 6.2 Application ......................... 87 6.2.1 From LEO (ISS) to LEO (Sun-Synchronous) ... 87 6.2.2 From LEO (ISS) to Molniya Orbit .. ...... 92 6.3 Uncertainties in Solution Optimality ........... 99 6.3.1 Motivation ...................... 99 6.3.2 Understanding the Solution Space ... ...... 102 6.4 Providing a Good Guess for DIDO ..... ....... 109 6.4.1 Guess Consistency ........ ......... 109 6.4.2 Engineering Judgment ......... ...... 109 7 Finite Burn Orbital Transfer 113 7.1 Capability Demonstration ........... ...... .... .. 113 7.1.1 Orbit-Raising Transfer ............... ... .... 114 7.1.2 Inclination Change on a Circular Orbit ...... ... .. 122 7.2 Application: From LEO (ISS) to LEO (Sun-Synchronous) with J2 .. 134 7.2.1 Basic Problem .................... .. ... 134 7.2.2 One Burn at a Time ... ............. .. .. ... 136 7.3 Solution Feasibility ............... ...... .. .. .. 138 7.3.1 Orbit-Raising Transfer ............... .. .. 139 7.3.2 Inclination Change Transfer ............ .. ... .. 146 7.3.3 From LEO (ISS) to LEO (Sun-Synchronous) with J2 -- . 149 8 Conclusion 151 8.1 Sum m ary ..... ..... ...... ..... ...... .... 151 8.2 Future Work. ..... ...... ..... ...... ..... .. 152 8 List of Figures 1-1 Continuous Controls .. ...... ...... ...... ....... 17 1-2 "Bang-Off-Bang" Continuous Controls ......... 18 1-3 Transfer Series . ...... ...... ....... ...... .... 20 2-1 Constrained Minimization: The Method of Lagrange .... ..... 24 4-1 Standard Node Distribution for the Legendre Pseudospectral Method (100 nodes) ....... ..... ..... ........ ... .. ... 46 6-1 Circular-Circular Hohmann Transfer: Random Guess ......... 66 6-2 Circular-Circular Hohmann Transfer: Guess Trajectory = Initial Orbit 67 6-3 Elliptical-Elliptical Hohmann Transfer: Random Guess ........ 69 6-4 Inclination Change Transfer: Initial & Final Orbits .. ........ 71 6-5 Inclination Change Transfer: Single Impulse Guess (-z) ....... 72 6-6 Inclination Change Transfer: Two-Impulse Guess (+z, -z) ...... 73 6-7 Inclination Change Transfer: Two-Impulse Guess (-z, +z) ... ... 75 6-8 Inclination/Node Change Transfer: Random Guess .......... 77 6-9 Inclination Change Transfer (Elliptical): Random Guess ...... 79 6-10 Size and Inclination Change Transfer: Random Guess ...... ... 82 6-11 Size and Inclination Change Transfer (Elliptical): Random Guess .. 85 6-12 LEO-LEO Transfer: Continuous Solution ...... .......... 88 6-13 LEO-LEO Transfer: Continuous Solution with Transformed Parame- terized G uess) ............ ........... ........ 90 6-14 LEO-LEO Transfer: Parameterized Guess and Two Solutions ..... 91 6-15 LEO-Molniya Transfer: Continuous Solution ..........
Load more

Recommended publications
  • Astrodynamics
    Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities
    [Show full text]
  • Maneuver Detection of Space Object for Space Surveillance
    MANEUVER DETECTION OF SPACE OBJECT FOR SPACE SURVEILLANCE Jian Huang*, Weidong Hu, Lefeng Zhang $756WDWH.H\/DE1DWLRQDO8QLYHUVLW\RI'HIHQVH7HFKQRORJ\&KDQJVKD+XQDQ3URYLQFH&KLQD (PDLOKXDQJMLDQ#QXGWHGXFQ ABSTRACT on the technique of a moving window curve fit. Holzinger & Scheeres presented an object correlation Maneuver detection is a very important task for and maneuver detection method using optimal control maintaining the catalog of the orbital objects and space performance metrics [5]. Kelecy & Jah focused on the situational awareness. This paper mainly focuses on the detection and reconstruction of single low thrust in- typical maneuver scenario where space objects only track maneuvers by using the orbit determination perform tangential orbital maneuvers during a relative strategies based on the batch least-squares and long gap. Particularly, only two classical and extended Kalman filter (EKF) [6]. However, these commonly applied orbital transition manners are methods are highly relevant to the presupposed considered, i.e. the twice tangential maneuvers at the maneuvering mode and a relative short observation gap. apogee and the perigee or one tangential maneuver at In this paper, to address the real observed data, we only an arbitrary time. Based on this, we preliminarily consider the common maneuvering modes and estimate the maneuvering mode and parameters by observation scenarios in practical. For an orbital analyzing the change of semi-major axis and maneuver, minimization of fuel consumption is eccentricity. Furthermore, if only one tangential essential because the weight of a payload that can be maneuver happened, we can formulate the estimation carried to the desired orbit depends on this problem of maneuvering parameters as a non-linear minimization.
    [Show full text]
  • Reduction of Saturn Orbit Insertion Impulse Using Deep-Space Low Thrust
    Reduction of Saturn Orbit Insertion Impulse using Deep-Space Low Thrust Elena Fantino ∗† Khalifa University of Science and Technology, Abu Dhabi, United Arab Emirates. Roberto Flores‡ International Center for Numerical Methods in Engineering, 08034 Barcelona, Spain. Jesús Peláez§ and Virginia Raposo-Pulido¶ Technical University of Madrid, 28040 Madrid, Spain. Orbit insertion at Saturn requires a large impulsive manoeuver due to the velocity difference between the spacecraft and the planet. This paper presents a strategy to reduce dramatically the hyperbolic excess speed at Saturn by means of deep-space electric propulsion. The inter- planetary trajectory includes a gravity assist at Jupiter, combined with low-thrust maneuvers. The thrust arc from Earth to Jupiter lowers the launch energy requirement, while an ad hoc steering law applied after the Jupiter flyby reduces the hyperbolic excess speed upon arrival at Saturn. This lowers the orbit insertion impulse to the point where capture is possible even with a gravity assist with Titan. The control-law algorithm, the benefits to the mass budget and the main technological aspects are presented and discussed. The simple steering law is compared with a trajectory optimizer to evaluate the quality of the results and possibilities for improvement. I. Introduction he giant planets have a special place in our quest for learning about the origins of our planetary system and Tour search for life, and robotic missions are essential tools for this scientific goal. Missions to the outer planets arXiv:2001.04357v1 [astro-ph.EP] 8 Jan 2020 have been prioritized by NASA and ESA, and this has resulted in important space projects for the exploration of the Jupiter system (NASA’s Europa Clipper [1] and ESA’s Jupiter Icy Moons Explorer [2]), and studies are underway to launch a follow-up of Cassini/Huygens called Titan Saturn System Mission (TSSM) [3], a joint ESA-NASA project.
    [Show full text]
  • A Hot Subdwarf-White Dwarf Super-Chandrasekhar Candidate
    A hot subdwarf–white dwarf super-Chandrasekhar candidate supernova Ia progenitor Ingrid Pelisoli1,2*, P. Neunteufel3, S. Geier1, T. Kupfer4,5, U. Heber6, A. Irrgang6, D. Schneider6, A. Bastian1, J. van Roestel7, V. Schaffenroth1, and B. N. Barlow8 1Institut fur¨ Physik und Astronomie, Universitat¨ Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam-Golm, Germany 2Department of Physics, University of Warwick, Coventry, CV4 7AL, UK 3Max Planck Institut fur¨ Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei Munchen¨ 4Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA 5Texas Tech University, Department of Physics & Astronomy, Box 41051, 79409, Lubbock, TX, USA 6Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nuremberg (FAU), Sternwartstr. 7, 96049 Bamberg, Germany 7Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 8Department of Physics and Astronomy, High Point University, High Point, NC 27268, USA *[email protected] ABSTRACT Supernova Ia are bright explosive events that can be used to estimate cosmological distances, allowing us to study the expansion of the Universe. They are understood to result from a thermonuclear detonation in a white dwarf that formed from the exhausted core of a star more massive than the Sun. However, the possible progenitor channels leading to an explosion are a long-standing debate, limiting the precision and accuracy of supernova Ia as distance indicators. Here we present HD 265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf — a stripped core-helium burning star.
    [Show full text]
  • Electric Propulsion System Scaling for Asteroid Capture-And-Return Missions
    Electric propulsion system scaling for asteroid capture-and-return missions Justin M. Little⇤ and Edgar Y. Choueiri† Electric Propulsion and Plasma Dynamics Laboratory, Princeton University, Princeton, NJ, 08544 The requirements for an electric propulsion system needed to maximize the return mass of asteroid capture-and-return (ACR) missions are investigated in detail. An analytical model is presented for the mission time and mass balance of an ACR mission based on the propellant requirements of each mission phase. Edelbaum’s approximation is used for the Earth-escape phase. The asteroid rendezvous and return phases of the mission are modeled as a low-thrust optimal control problem with a lunar assist. The numerical solution to this problem is used to derive scaling laws for the propellant requirements based on the maneuver time, asteroid orbit, and propulsion system parameters. Constraining the rendezvous and return phases by the synodic period of the target asteroid, a semi- empirical equation is obtained for the optimum specific impulse and power supply. It was found analytically that the optimum power supply is one such that the mass of the propulsion system and power supply are approximately equal to the total mass of propellant used during the entire mission. Finally, it is shown that ACR missions, in general, are optimized using propulsion systems capable of processing 100 kW – 1 MW of power with specific impulses in the range 5,000 – 10,000 s, and have the potential to return asteroids on the order of 103 104 tons. − Nomenclature
    [Show full text]
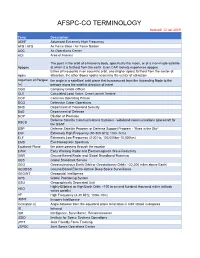
  • AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
    AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance
    [Show full text]
  • Download Paper
    Ever Wonder What’s in Molniya? We Do. John T. McGraw J. T. McGraw and Associates, LLC and University of New Mexico Peter C. Zimmer J. T. McGraw and Associates, LLC Mark R. Ackermann J. T. McGraw and Associates, LLC ABSTRACT Molniya orbits are high inclination, high eccentricity orbits which provide the utility of long apogee dwell time over northern continents, with the additional benefit of obviating the largest orbital perturbation introduced by the Earth’s nonspherical (oblate) gravitational potential. We review the few earlier surveys of the Molniya domain and evaluate results from a new, large area unbiased survey of the northern Molniya domain. We detect 120 Molniya objects in a three hour survey of ~ 1300 square degrees of the sky to a limiting magnitude of about 16.5. Future Molniya surveys will discover a significant number of objects, including debris, and monitoring these objects might provide useful data with respect to orbital perturbations including solar radiation and Earth atmosphere drag effects. 1. SPECIALIZED ORBITS Earth Orbital Space (EOS) supports many versions of specialized satellite orbits defined by a combination of satellite mission and orbital dynamics. Surely the most well-known family of specialized orbits is the geostationary orbits proposed by science fiction author Arthur C. Clarke in 1945 [1] that lie sensibly in the plane of Earth’s equator, with orbital period that matches the Earth’s rotation period. Satellites in these orbits, and the closely related geosynchronous orbits, appear from Earth to remain constantly overhead, allowing continuous communication with the majority of the hemisphere below. Constellations of three geostationary satellites equally spaced in orbit (~ 120° separation) can maintain near-global communication and terrestrial surveillance.
    [Show full text]
  • Use of MESSENGER Radioscience Data to Improve Planetary Ephemeris and to Test General Relativity
    A&A 561, A115 (2014) Astronomy DOI: 10.1051/0004-6361/201322124 & © ESO 2014 Astrophysics Use of MESSENGER radioscience data to improve planetary ephemeris and to test general relativity A. K. Verma1;2, A. Fienga3;4, J. Laskar4, H. Manche4, and M. Gastineau4 1 Observatoire de Besançon, UTINAM-CNRS UMR6213, 41bis avenue de l’Observatoire, 25000 Besançon, France e-mail: [email protected] 2 Centre National d’Études Spatiales, 18 avenue Édouard Belin, 31400 Toulouse, France 3 Observatoire de la Côte d’Azur, GéoAzur-CNRS UMR7329, 250 avenue Albert Einstein, 06560 Valbonne, France 4 Astronomie et Systèmes Dynamiques, IMCCE-CNRS UMR8028, 77 Av. Denfert-Rochereau, 75014 Paris, France Received 24 June 2013 / Accepted 7 November 2013 ABSTRACT The current knowledge of Mercury’s orbit has mainly been gained by direct radar ranging obtained from the 60s to 1998 and by five Mercury flybys made with Mariner 10 in the 70s, and with MESSENGER made in 2008 and 2009. On March 18, 2011, MESSENGER became the first spacecraft to orbit Mercury. The radioscience observations acquired during the orbital phase of MESSENGER drastically improved our knowledge of the orbit of Mercury. An accurate MESSENGER orbit is obtained by fitting one-and-half years of tracking data using GINS orbit determination software. The systematic error in the Earth-Mercury geometric positions, also called range bias, obtained from GINS are then used to fit the INPOP dynamical modeling of the planet motions. An improved ephemeris of the planets is then obtained, INPOP13a, and used to perform general relativity tests of the parametrized post-Newtonian (PPN) formalism.
    [Show full text]
  • Positioning: Drift Orbit and Station Acquisition
    Orbits Supplement GEOSTATIONARY ORBIT PERTURBATIONS INFLUENCE OF ASPHERICITY OF THE EARTH: The gravitational potential of the Earth is no longer µ/r, but varies with longitude. A tangential acceleration is created, depending on the longitudinal location of the satellite, with four points of stable equilibrium: two stable equilibrium points (L 75° E, 105° W) two unstable equilibrium points ( 15° W, 162° E) This tangential acceleration causes a drift of the satellite longitude. Longitudinal drift d'/dt in terms of the longitude about a point of stable equilibrium expresses as: (d/dt)2 - k cos 2 = constant Orbits Supplement GEO PERTURBATIONS (CONT'D) INFLUENCE OF EARTH ASPHERICITY VARIATION IN THE LONGITUDINAL ACCELERATION OF A GEOSTATIONARY SATELLITE: Orbits Supplement GEO PERTURBATIONS (CONT'D) INFLUENCE OF SUN & MOON ATTRACTION Gravitational attraction by the sun and moon causes the satellite orbital inclination to change with time. The evolution of the inclination vector is mainly a combination of variations: period 13.66 days with 0.0035° amplitude period 182.65 days with 0.023° amplitude long term drift The long term drift is given by: -4 dix/dt = H = (-3.6 sin M) 10 ° /day -4 diy/dt = K = (23.4 +.2.7 cos M) 10 °/day where M is the moon ascending node longitude: M = 12.111 -0.052954 T (T: days from 1/1/1950) 2 2 2 2 cos d = H / (H + K ); i/t = (H + K ) Depending on time within the 18 year period of M d varies from 81.1° to 98.9° i/t varies from 0.75°/year to 0.95°/year Orbits Supplement GEO PERTURBATIONS (CONT'D) INFLUENCE OF SUN RADIATION PRESSURE Due to sun radiation pressure, eccentricity arises: EFFECT OF NON-ZERO ECCENTRICITY L = difference between longitude of geostationary satellite and geosynchronous satellite (24 hour period orbit with e0) With non-zero eccentricity the satellite track undergoes a periodic motion about the subsatellite point at perigee.
    [Show full text]
  • Molniya" Type Orbits
    EXAMINATION OF THE LIFETIME, EVOLUTION AND RE-ENTRY FEATURES FOR THE "MOLNIYA" TYPE ORBITS Yu.F. Kolyuka, N.M. Ivanov, T.I. Afanasieva, T.A. Gridchina Mission Control Center, 4, Pionerskaya str., Korolev, Moscow Region, 141070, Russia, [email protected] ABSTRACT Space vehicles of the "Molniya" series, launched into the special highly elliptical orbits with a period of ~ 12 hours, are intended for solution of telecommunication problems in stretched territories of the former USSR and nowadays − Russia, and also for providing the connectivity between Russia and other countries. The inclination of standard orbits of such a kind of satellites is near to the critical value i ≈ 63.4 deg and their initial minimal altitude normally has a value Hmin ~ 500 km. As a rule, the “Molniya" satellites of a concrete series form the groups with determined disposition of orbital planes on an ascending node longitude that allows to ensure requirements of the continuous link between any points in northern hemisphere. The first satellite of the "Molniya" series has been inserted into designed orbit in 1964. Up to now it is launched over 160 space vehicles of such a kind. As well as all artificial satellites, space vehicles "Molniya" undergo the action of various perturbing forces influencing a change of their orbital parameters. However in case of space vehicles "Molniya" these changes of parameters have a specific character and in many things they differ from the perturbations which are taking place for the majority of standard orbits of the artificial satellites with rather small eccentricity. In particular, to strong enough variations (first of all, at the expense of the luni-solar attraction) it is subjected the orbit perigee distance rπ that can lead to such reduction Hmin when further flight of the satellite on its orbit becomes impossible, it re-entries and falls to the Earth.
    [Show full text]
  • Multi-Body Trajectory Design Strategies Based on Periapsis Poincaré Maps
    MULTI-BODY TRAJECTORY DESIGN STRATEGIES BASED ON PERIAPSIS POINCARÉ MAPS A Dissertation Submitted to the Faculty of Purdue University by Diane Elizabeth Craig Davis In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy August 2011 Purdue University West Lafayette, Indiana ii To my husband and children iii ACKNOWLEDGMENTS I would like to thank my advisor, Professor Kathleen Howell, for her support and guidance. She has been an invaluable source of knowledge and ideas throughout my studies at Purdue, and I have truly enjoyed our collaborations. She is an inspiration to me. I appreciate the insight and support from my committee members, Professor James Longuski, Professor Martin Corless, and Professor Daniel DeLaurentis. I would like to thank the members of my research group, past and present, for their friendship and collaboration, including Geoff Wawrzyniak, Chris Patterson, Lindsay Millard, Dan Grebow, Marty Ozimek, Lucia Irrgang, Masaki Kakoi, Raoul Rausch, Matt Vavrina, Todd Brown, Amanda Haapala, Cody Short, Mar Vaquero, Tom Pavlak, Wayne Schlei, Aurelie Heritier, Amanda Knutson, and Jeff Stuart. I thank my parents, David and Jeanne Craig, for their encouragement and love throughout my academic career. They have cheered me on through many years of studies. I am grateful for the love and encouragement of my husband, Jonathan. His never-ending patience and friendship have been a constant source of support. Finally, I owe thanks to the organizations that have provided the funding opportunities that have supported me through my studies, including the Clare Booth Luce Foundation, Zonta International, and Purdue University and the School of Aeronautics and Astronautics through the Graduate Assistance in Areas of National Need and the Purdue Forever Fellowships.
    [Show full text]
  • Open Rosen Thesis.Pdf
    THE PENNSYLVANIA STATE UNIVERSITY SCHREYER HONORS COLLEGE DEPARTMENT OF AEROSPACE ENGINEERING END OF LIFE DISPOSAL OF SATELLITES IN HIGHLY ELLIPTICAL ORBITS MITCHELL ROSEN SPRING 2019 A thesis submitted in partial fulfillment of the requirements for a baccalaureate degree in Aerospace Engineering with honors in Aerospace Engineering Reviewed and approved* by the following: Dr. David Spencer Professor of Aerospace Engineering Thesis Supervisor Dr. Mark Maughmer Professor of Aerospace Engineering Honors Adviser * Signatures are on file in the Schreyer Honors College. i ABSTRACT Highly elliptical orbits allow for coverage of large parts of the Earth through a single satellite, simplifying communications in the globe’s northern reaches. These orbits are able to avoid drastic changes to the argument of periapse by using a critical inclination (63.4°) that cancels out the first level of the geopotential forces. However, this allows the next level of geopotential forces to take over, quickly de-orbiting satellites. Thus, a balance between the rate of change of the argument of periapse and the lifetime of the orbit is necessitated. This thesis sets out to find that balance. It is determined that an orbit with an inclination of 62.5° strikes that balance best. While this orbit is optimal off of the critical inclination, it is still near enough that to allow for potential use of inclination changes as a deorbiting method. Satellites are deorbited when the propellant remaining is enough to perform such a maneuver, and nothing more; therefore, the less change in velocity necessary for to deorbit, the better. Following the determination of an ideal highly elliptical orbit, the different methods of inclination change is tested against the usual method for deorbiting a satellite, an apoapse burn to lower the periapse, to find the most propellant- efficient method.
    [Show full text]