Applied Reliabilty Class Notes in Powerpoint
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Study of Non-Central Skew T Distributions and Their Applications in Data Analysis and Change Point Detection
A STUDY OF NON-CENTRAL SKEW T DISTRIBUTIONS AND THEIR APPLICATIONS IN DATA ANALYSIS AND CHANGE POINT DETECTION Abeer M. Hasan A Dissertation Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY August 2013 Committee: Arjun K. Gupta, Co-advisor Wei Ning, Advisor Mark Earley, Graduate Faculty Representative Junfeng Shang. Copyright c August 2013 Abeer M. Hasan All rights reserved iii ABSTRACT Arjun K. Gupta, Co-advisor Wei Ning, Advisor Over the past three decades there has been a growing interest in searching for distribution families that are suitable to analyze skewed data with excess kurtosis. The search started by numerous papers on the skew normal distribution. Multivariate t distributions started to catch attention shortly after the development of the multivariate skew normal distribution. Many researchers proposed alternative methods to generalize the univariate t distribution to the multivariate case. Recently, skew t distribution started to become popular in research. Skew t distributions provide more flexibility and better ability to accommodate long-tailed data than skew normal distributions. In this dissertation, a new non-central skew t distribution is studied and its theoretical properties are explored. Applications of the proposed non-central skew t distribution in data analysis and model comparisons are studied. An extension of our distribution to the multivariate case is presented and properties of the multivariate non-central skew t distri- bution are discussed. We also discuss the distribution of quadratic forms of the non-central skew t distribution. In the last chapter, the change point problem of the non-central skew t distribution is discussed under different settings. -

On the Meaning and Use of Kurtosis
Psychological Methods Copyright 1997 by the American Psychological Association, Inc. 1997, Vol. 2, No. 3,292-307 1082-989X/97/$3.00 On the Meaning and Use of Kurtosis Lawrence T. DeCarlo Fordham University For symmetric unimodal distributions, positive kurtosis indicates heavy tails and peakedness relative to the normal distribution, whereas negative kurtosis indicates light tails and flatness. Many textbooks, however, describe or illustrate kurtosis incompletely or incorrectly. In this article, kurtosis is illustrated with well-known distributions, and aspects of its interpretation and misinterpretation are discussed. The role of kurtosis in testing univariate and multivariate normality; as a measure of departures from normality; in issues of robustness, outliers, and bimodality; in generalized tests and estimators, as well as limitations of and alternatives to the kurtosis measure [32, are discussed. It is typically noted in introductory statistics standard deviation. The normal distribution has a kur- courses that distributions can be characterized in tosis of 3, and 132 - 3 is often used so that the refer- terms of central tendency, variability, and shape. With ence normal distribution has a kurtosis of zero (132 - respect to shape, virtually every textbook defines and 3 is sometimes denoted as Y2)- A sample counterpart illustrates skewness. On the other hand, another as- to 132 can be obtained by replacing the population pect of shape, which is kurtosis, is either not discussed moments with the sample moments, which gives or, worse yet, is often described or illustrated incor- rectly. Kurtosis is also frequently not reported in re- ~(X i -- S)4/n search articles, in spite of the fact that virtually every b2 (•(X i - ~')2/n)2' statistical package provides a measure of kurtosis. -

A Multivariate Student's T-Distribution
Open Journal of Statistics, 2016, 6, 443-450 Published Online June 2016 in SciRes. http://www.scirp.org/journal/ojs http://dx.doi.org/10.4236/ojs.2016.63040 A Multivariate Student’s t-Distribution Daniel T. Cassidy Department of Engineering Physics, McMaster University, Hamilton, ON, Canada Received 29 March 2016; accepted 14 June 2016; published 17 June 2016 Copyright © 2016 by author and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract A multivariate Student’s t-distribution is derived by analogy to the derivation of a multivariate normal (Gaussian) probability density function. This multivariate Student’s t-distribution can have different shape parameters νi for the marginal probability density functions of the multi- variate distribution. Expressions for the probability density function, for the variances, and for the covariances of the multivariate t-distribution with arbitrary shape parameters for the marginals are given. Keywords Multivariate Student’s t, Variance, Covariance, Arbitrary Shape Parameters 1. Introduction An expression for a multivariate Student’s t-distribution is presented. This expression, which is different in form than the form that is commonly used, allows the shape parameter ν for each marginal probability density function (pdf) of the multivariate pdf to be different. The form that is typically used is [1] −+ν Γ+((ν n) 2) T ( n) 2 +Σ−1 n 2 (1.[xx] [ ]) (1) ΓΣ(νν2)(π ) This “typical” form attempts to generalize the univariate Student’s t-distribution and is valid when the n marginal distributions have the same shape parameter ν . -

A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess
S S symmetry Article A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess Guillermo Martínez-Flórez 1, Víctor Leiva 2,* , Emilio Gómez-Déniz 3 and Carolina Marchant 4 1 Departamento de Matemáticas y Estadística, Facultad de Ciencias Básicas, Universidad de Córdoba, Montería 14014, Colombia; [email protected] 2 Escuela de Ingeniería Industrial, Pontificia Universidad Católica de Valparaíso, 2362807 Valparaíso, Chile 3 Facultad de Economía, Empresa y Turismo, Universidad de Las Palmas de Gran Canaria and TIDES Institute, 35001 Canarias, Spain; [email protected] 4 Facultad de Ciencias Básicas, Universidad Católica del Maule, 3466706 Talca, Chile; [email protected] * Correspondence: [email protected] or [email protected] Received: 30 June 2020; Accepted: 19 August 2020; Published: 1 September 2020 Abstract: In this paper, we consider skew-normal distributions for constructing new a distribution which allows us to model proportions and rates with zero/one inflation as an alternative to the inflated beta distributions. The new distribution is a mixture between a Bernoulli distribution for explaining the zero/one excess and a censored skew-normal distribution for the continuous variable. The maximum likelihood method is used for parameter estimation. Observed and expected Fisher information matrices are derived to conduct likelihood-based inference in this new type skew-normal distribution. Given the flexibility of the new distributions, we are able to show, in real data scenarios, the good performance of our proposal. Keywords: beta distribution; centered skew-normal distribution; maximum-likelihood methods; Monte Carlo simulations; proportions; R software; rates; zero/one inflated data 1. -

A Study of Ocean Wave Statistical Properties Using SNOW
A study of ocean wave statistical properties using nonlinear, directional, phase- resolved ocean wavefield simulations Legena Henry PhD Candidate Course 2 – OE [email protected] abstract We study the statistics of wavefields obtained from phase-resolved simulations that are non-linear (up to the third order in surface potential). We model wave-wave interactions based on the fully non- linear Zakharov equations. We vary the simulated wavefield's input spectral properties: peak shape parameter, Phillips parameter and Directional Spreading Function. We then investigate the relationships between these input spectral properties and output physical properties via statistical analysis. We investigate: 1. Surface elevation distribution in response to input spectral properties, 2. Wave definition methods in an irregular wavefield with a two- dimensional wave number, 3. Wave height/wavelength distributions in response to input spectral properties, including the occurrence and spacing of large wave events (based on definitions in 2). 1. Surface elevation distribution in response to input spectral properties: – Peak Shape Parameter – Phillips' Parameter – Directional Spreading Function 1. Surface elevation distribution in response to input spectral properties: Peak shape parameter Peak shape parameter produces higher impact on even moments of surface elevation, (i.e. surface elevation kurtosis and surface elevation variance) than on the observed odd moments (skewness) of surface elevation. The highest elevations in a wavefield with mean peak shape parameter, 3.3 are more stable than those in wavefields with mean peak shape parameter, 1.0, and 5.0 We find surface elevation kurtosis in non-linear wavefields is much smaller than surface elevation slope kurtosis. We also see that higher values of peak shape parameter produce higher kurtosis of surface slope in the mean direction of propagation. -

Procedures for Estimation of Weibull Parameters James W
United States Department of Agriculture Procedures for Estimation of Weibull Parameters James W. Evans David E. Kretschmann David W. Green Forest Forest Products General Technical Report February Service Laboratory FPL–GTR–264 2019 Abstract Contents The primary purpose of this publication is to provide an 1 Introduction .................................................................. 1 overview of the information in the statistical literature on 2 Background .................................................................. 1 the different methods developed for fitting a Weibull distribution to an uncensored set of data and on any 3 Estimation Procedures .................................................. 1 comparisons between methods that have been studied in the 4 Historical Comparisons of Individual statistics literature. This should help the person using a Estimator Types ........................................................ 8 Weibull distribution to represent a data set realize some advantages and disadvantages of some basic methods. It 5 Other Methods of Estimating Parameters of should also help both in evaluating other studies using the Weibull Distribution .......................................... 11 different methods of Weibull parameter estimation and in 6 Discussion .................................................................. 12 discussions on American Society for Testing and Materials Standard D5457, which appears to allow a choice for the 7 Conclusion ................................................................ -
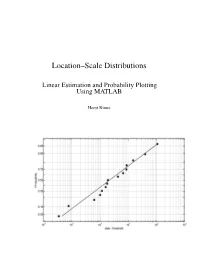
Location-Scale Distributions
Location–Scale Distributions Linear Estimation and Probability Plotting Using MATLAB Horst Rinne Copyright: Prof. em. Dr. Horst Rinne Department of Economics and Management Science Justus–Liebig–University, Giessen, Germany Contents Preface VII List of Figures IX List of Tables XII 1 The family of location–scale distributions 1 1.1 Properties of location–scale distributions . 1 1.2 Genuine location–scale distributions — A short listing . 5 1.3 Distributions transformable to location–scale type . 11 2 Order statistics 18 2.1 Distributional concepts . 18 2.2 Moments of order statistics . 21 2.2.1 Definitions and basic formulas . 21 2.2.2 Identities, recurrence relations and approximations . 26 2.3 Functions of order statistics . 32 3 Statistical graphics 36 3.1 Some historical remarks . 36 3.2 The role of graphical methods in statistics . 38 3.2.1 Graphical versus numerical techniques . 38 3.2.2 Manipulation with graphs and graphical perception . 39 3.2.3 Graphical displays in statistics . 41 3.3 Distribution assessment by graphs . 43 3.3.1 PP–plots and QQ–plots . 43 3.3.2 Probability paper and plotting positions . 47 3.3.3 Hazard plot . 54 3.3.4 TTT–plot . 56 4 Linear estimation — Theory and methods 59 4.1 Types of sampling data . 59 IV Contents 4.2 Estimators based on moments of order statistics . 63 4.2.1 GLS estimators . 64 4.2.1.1 GLS for a general location–scale distribution . 65 4.2.1.2 GLS for a symmetric location–scale distribution . 71 4.2.1.3 GLS and censored samples . -

Power Birnbaum-Saunders Student T Distribution
Revista Integración Escuela de Matemáticas Universidad Industrial de Santander H Vol. 35, No. 1, 2017, pág. 51–70 Power Birnbaum-Saunders Student t distribution Germán Moreno-Arenas a ∗, Guillermo Martínez-Flórez b Heleno Bolfarine c a Universidad Industrial de Santander, Escuela de Matemáticas, Bucaramanga, Colombia. b Universidad de Córdoba, Departamento de Matemáticas y Estadística, Montería, Colombia. c Universidade de São Paulo, Departamento de Estatística, São Paulo, Brazil. Abstract. The fatigue life distribution proposed by Birnbaum and Saunders has been used quite effectively to model times to failure for materials sub- ject to fatigue. In this article, we introduce an extension of the classical Birnbaum-Saunders distribution substituting the normal distribution by the power Student t distribution. The new distribution is more flexible than the classical Birnbaum-Saunders distribution in terms of asymmetry and kurto- sis. We discuss maximum likelihood estimation of the model parameters and associated regression model. Two real data set are analysed and the results reveal that the proposed model better some other models proposed in the literature. Keywords: Birnbaum-Saunders distribution, alpha-power distribution, power Student t distribution. MSC2010: 62-07, 62F10, 62J02, 62N86. Distribución Birnbaum-Saunders Potencia t de Student Resumen. La distribución de probabilidad propuesta por Birnbaum y Saun- ders se ha usado con bastante eficacia para modelar tiempos de falla de ma- teriales sujetos a la fátiga. En este artículo definimos una extensión de la distribución Birnbaum-Saunders clásica sustituyendo la distribución normal por la distribución potencia t de Student. La nueva distribución es más flexi- ble que la distribución Birnbaum-Saunders clásica en términos de asimetría y curtosis. -

Performance of the Maximum Likelihood Estimators for the Parameters of Multivariate Generalized Gaussian Distributions
Performance of the maximum likelihood estimators for the parameters of multivariate generalized Gaussian distributions Lionel Bombrun, Frédéric Pascal, Jean-Yves Tourneret, Yannick Berthoumieu To cite this version: Lionel Bombrun, Frédéric Pascal, Jean-Yves Tourneret, Yannick Berthoumieu. Performance of the maximum likelihood estimators for the parameters of multivariate generalized Gaussian distributions. IEEE International Conference on Acoustics, Speech, and Signal Processing, Mar 2012, Kyoto, Japan. pp.3525 - 3528, 10.1109/ICASSP.2012.6288677. hal-00744600 HAL Id: hal-00744600 https://hal.archives-ouvertes.fr/hal-00744600 Submitted on 23 Oct 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. PERFORMANCE OF THE MAXIMUM LIKELIHOOD ESTIMATORS FOR THE PARAMETERS OF MULTIVARIATE GENERALIZED GAUSSIAN DISTRIBUTIONS Lionel Bombrun1, Fred´ eric´ Pascal2 ,Jean-Yves Tourneret3 and Yannick Berthoumieu1 1 : Universite´ de Bordeaux, ENSEIRB-Matmeca, Laboratoire IMS, Groupe Signal et Image flionel.bombrun, yannick.berthoumieu [email protected] 2 : SONDRA, Supelec,´ Plateau du Moulon, [email protected] 3 : Universite´ de Toulouse, IRIT/INP-ENSEEIHT, [email protected] ABSTRACT (which corresponds to most of the real-life problems), the maximum likelihood estimator (MLE) of the MGGD scatter matrix exists and This paper studies the performance of the maximum likelihood esti- is unique up to a scalar factor. -

Parametric Forecasting of Value at Risk Using Heavy-Tailed Distribution
REVISTA INVESTIGACIÓN OPERACIONAL _____ Vol., 30, No.1, 32-39, 2009 DEPENDENCE BETWEEN VOLATILITY PERSISTENCE, KURTOSIS AND DEGREES OF FREEDOM Ante Rozga1 and Josip Arnerić, 2 Faculty of Economics, University of Split, Croatia ABSTRACT In this paper the dependence between volatility persistence, kurtosis and degrees of freedom from Student’s t-distribution will be presented in estimation alternative risk measures on simulated returns. As the most used measure of market risk is standard deviation of returns, i.e. volatility. However, based on volatility alternative risk measures can be estimated, for example Value-at-Risk (VaR). There are many methodologies for calculating VaR, but for simplicity they can be classified into parametric and nonparametric models. In category of parametric models the GARCH(p,q) model is used for modeling time-varying variance of returns. KEY WORDS: Value-at-Risk, GARCH(p,q), T-Student MSC 91B28 RESUMEN En este trabajo la dependencia de la persistencia de la volatilidad, kurtosis y grados de liberad de una Distribución T-Student será presentada como una alternativa para la estimación de medidas de riesgo en la simulación de los retornos. La medida más usada de riesgo de mercado es la desviación estándar de los retornos, i.e. volatilidad. Sin embargo, medidas alternativas de la volatilidad pueden ser estimadas, por ejemplo el Valor-al-Riesgo (Value-at-Risk, VaR). Existen muchas metodologías para calcular VaR, pero por simplicidad estas pueden ser clasificadas en modelos paramétricos y no paramétricos . En la categoría de modelos paramétricos el modelo GARCH(p,q) es usado para modelar la varianza de retornos que varían en el tiempo. -

Bayesian Life Test Planning for the Log-Location-Scale Family of Distributions" (2014)
Statistics Preprints Statistics 3-2014 Bayesian Life Test Planning for the Log-Location- Scale Family of Distributions Yili Hong Virginia Tech Caleb King Virginia Tech Yao Zhang Pfizer Global Research and Development William Q. Meeker Iowa State University, [email protected] Follow this and additional works at: http://lib.dr.iastate.edu/stat_las_preprints Part of the Statistics and Probability Commons Recommended Citation Hong, Yili; King, Caleb; Zhang, Yao; and Meeker, William Q., "Bayesian Life Test Planning for the Log-Location-Scale Family of Distributions" (2014). Statistics Preprints. 131. http://lib.dr.iastate.edu/stat_las_preprints/131 This Article is brought to you for free and open access by the Statistics at Iowa State University Digital Repository. It has been accepted for inclusion in Statistics Preprints by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Bayesian Life Test Planning for the Log-Location-Scale Family of Distributions Abstract This paper describes Bayesian methods for life test planning with censored data from a log-location-scale distribution, when prior information of the distribution parameters is available. We use a Bayesian criterion based on the estimation precision of a distribution quantile. A large sample normal approximation gives a simplified, easy-tointerpret, yet valid approach to this planning problem, where in general no closed form solutions are available. To illustrate this approach, we present numerical investigations using the Weibull distribution with Type II censoring. We also assess the effects of prior distribution choice. A simulation approach of the same Bayesian problem is also presented as a tool for visualization and validation. -

Multivariate Student Versus Multivariate Gaussian Regression Models with Application to Finance
Journal of Risk and Financial Management Article Multivariate Student versus Multivariate Gaussian Regression Models with Application to Finance Thi Huong An Nguyen 1,2,†, Anne Ruiz-Gazen 1,*,†, Christine Thomas-Agnan 1,† and Thibault Laurent 3,† 1 Toulouse School of Economics, University of Toulouse Capitole, 21 allée de Brienne, 31000 Toulouse, France; [email protected] (T.H.A.N.); [email protected] (C.T.-A.) 2 Department of Economics, DaNang Architecture University, Da Nang 550000, Vietnam 3 Toulouse School of Economics, CNRS, University of Toulouse Capitole, 31000 Toulouse, France; [email protected] * Correspondence: [email protected]; Tel.: +33-561-12-8767 † These authors contributed equally to this work. Received: 29 December 2018; Accepted: 31 January 2019; Published: 9 February 2019 Abstract: To model multivariate, possibly heavy-tailed data, we compare the multivariate normal model (N) with two versions of the multivariate Student model: the independent multivariate Student (IT) and the uncorrelated multivariate Student (UT). After recalling some facts about these distributions and models, known but scattered in the literature, we prove that the maximum likelihood estimator of the covariance matrix in the UT model is asymptotically biased and propose an unbiased version. We provide implementation details for an iterative reweighted algorithm to compute the maximum likelihood estimators of the parameters of the IT model. We present a simulation study to compare the bias and root mean squared error of the ensuing estimators of the regression coefficients and covariance matrix under several scenarios of the potential data-generating process, misspecified or not.